Quadriques Architecturales
(I)...
Le Paraboloïde
Hyperbolique
| modèle z =
x² - y² ( ou z =
xy ) |
Son nom est compliqué pour celui qui le découvre -et souvent l'écorche! ; pourtant
rien n'est plus simple que ses équations,
rien n'est plus familier
que sa forme dans la nature ou les objets. Avant de voir les belles
réalisations architecturales que permet cette surface, démystifions son
nom! Pour cela, observons en même temps un objet associé aux loisirs
(faire de l'équitation, ou...
regarder un western)
et un modèle mathématique (destiné, jadis, à l'enseignement) conservé
dans un haut lieu de cette science: ne voit-on pas la même chose?
Paraboloïde? Etymologiquement, "en forme de parabole". Les coutures de la selle dont des paraboles, toutes avec
leur concavité vers le bas; dans les plans parallèles
x = a, ce sont les
z = a² - y² . C'est à dire qu'on a fixé des valeurs de
x, régulièrement échelonnées; dans chaque tranche la couture est une parabole. Sur le modèle en plâtre, seule
x = 0, ce sont les
z = - y² a été gravée.: c'est, lschématisée, la position des jambes du cavalier, si on les réduit à un fil.
Mais une deuxième, bien différente, apparait sur le modèle, dans un plan perpendiculaire (en l'occurence, y = 0 )
, avec
la concavité cette fois vers le haut: z = x²
, mais, si vous n'aimez pas les équations, c'est, sur la selle, la
ligne qui joint le pommeau à l'arrière de la selle -ou, si l'on
préfère, suit le dos du cheval- elle aussi matérialisée par une couture
(agrandissez pour avoir une chance de l'apercevoir!). Il suffirait pour
décrire parfaitement la surface, de dire que c'est la famille des
paraboles du premier type, dont le sommet glisse le long de la seconde.
Hyperbolique? Cela se réfère aux sections horizontales
z = h, ( ce sont les
h = x² - y²
), bien en évidence sur le modèle en plâtre. Elles ne figurent pas sur
la selle, mais il serait très facile de les faire apparaître: imaginez
que le cow-boy traverse une rivière calme, et s'engage de plus en plus
profond: ces hyperboles sont la marque laissée par le niveau de l'eau!
(Au moment crucial où le héros va ressentir la fraîcheur à l'endroit le
plus sensible de son individu, il pourra s'écrier: "Oh, bon sang! Deux
droites!" ...
car 0 = x² - y² = ( x - y ).( x + y ) revient à x - y = 0 ou x + y = 0
L'allure est celle d'un col en montagne;
le paraboloïde hyperbolique en est le modèle idéal et l'approximation
la plus simple (si on se limite aux termes de degré 2). Les deux
paraboles
"principales" sont la
ligne de crête (de sommet à sommet) et la
ligne de thalweg (de vallée à vallée), selon le vocabulaire géographique en usage pour un col), les hyperboles sont les
lignes de niveau (courbes d'altitude constante).
|
|
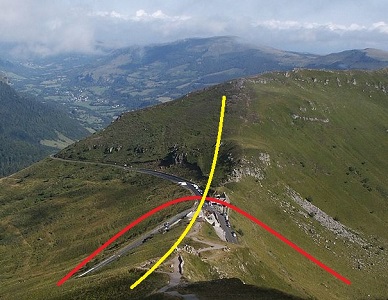
Pas de Peyrol, vu du Puy Mary (Cantal)
jaune: ligne de crête; rouge: ligne de thalweg
(image source sur Wikipedia Commons)
|
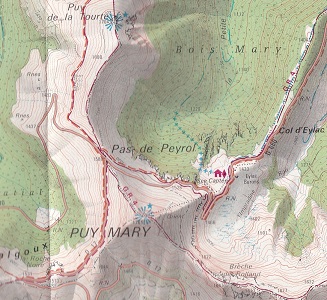
extrait de carte IGN (1/25000éme) cporrespondante.
l'allure des lignes de niveau est, localement, hyperbolique
|
On ne s'étonnera donc pas que les mathématiciens parlent indifféremment, dans cette situation, de point-col ou de point-selle
. Ils disent aussi P.H. plutôt que paraboloÏde hyperbolique, et comme
c'est plus rapide à dire ou à écrire, on ne ds'en privera pas dans la
suite.
En faire un toit? Mais c'est intuitif!
Et pour commencer, on a
dégoté pour vous l'apparition -un peu sommaire, certes!-
des hyperboles dans une forme d'habitat traditionnel des Pouilles, les
fameux trulli d'Alberobello,
inscrits au Patrimoine Mondial par l'UNESCO en 1996. Souvent, ces
peites maisons à toits de lauzes, sans aucun mortier, sont
isolées, à toit conique; mais il arrive que deux
circonstances se combienent heureusement:
- une forme en dôme (parabolique?) plutôt qu'un cône;
- la proximité de deux constructions, qui force au raccordement
de deux toits, l'ensemble prenant à la jonction une allure de
selle.
Et comme les lauzes sont posées horizontalement, elles dessinent localement, au voisinage du point selle, (et grossièrement) les hyperboles lignes de niveau d'un P.H. ...

|

|
Trulli "jumelés" à Alberobello (Italie): vue générale
|

|

|
Les lignes de niveau sont hyperboliques...
|
... les lignes de crête à crête paraboliques...
... les lignes de vallée à vallée aussi! (concavité vers le bas)
|
La parabole "de jonction" à
une fonction bien concrète: l'écoulement naturel de l'eau
de pluie. Car, ainsi qu'en attestent nos images, il peut même
pleuvoir ou faire un temps horriblement gris en Italie du Sud! En tout
cas, ces braves habitants ont construit ainsi des P.H. fort
intuitivement, sans connaissance des mathématiques. Ils ne sont pas les
seuls!
Cependant, dès qu'une demeure est un
peu plus grande, il faut une charpente au toit, laquelle est
essentiellement faite de poutres rectilignes. C'est ici qu'intervient
la deuxième forme d'équation, qui va mettre en évidence sa génération doublement
réglée.
Posant en effet X = x + y , Y = x - y , c'est à dire par un simple changement de repèree, l'équation en devient
z = X Y
(
z = 2 XY pour un changement orthonormé,
mais ce nest pas indispensable), on constate que la surface peut être décrite par
deux familles de droites:
(Da) : X = a , z = a Y et (Δb) : Y = b , z = X b
L'architecte, qui voulait bâtir un toit qui fasse écho au paysage du
Val d'Aran (Pyrénée), qui,
derrière la maison, dessine un col, n'a eu qu'à appliquer ce
principe... mais avec d'autant plus de mérite que la géométrie n'est
pas, en France, le point fort de la formation qu'il a le plus
probablement reçue! Bravo aussi au charpentier qui l'a réalisée, sans
être effrayé à l'idée de sortir des sentiers battus. Le résultat est
éloquent:


Images
parues dans une revue ayant pour thème la maison
individuelle, circa 1980
Architecte: Luc Demolombe
Plus étonnant, voici de quoi prouver qu'avec de la réflexion et du sens
pratique, on peut se transformer en mathématicien qui s'ignore. En inventant le P.H. comme solution à un problème technique,
sans avoir étudié les surfaces ni écrit la moindre équation. Le
bâtiment n'est qu'un petit garage, à loger dans la pointe d'un terrain
en angle aigu entre deux voies. Mais le règlement d'urbanisme imposait
au propriétaire qu'un mur soit parallèle à celui de sa maison, et le
faîtage parallèle ou perpendiculaire à celui de la maison, contrainte
assez courante pour éviter l'anarchie des orientations.
Au sol, il lui était facile de définir le plan par les deux petites
rues, et leurs perpendiculaires, dessinant un quadrilatère en forme de
cerf-volant. Mais qu'en est-il des contraintes sur la charpente?.

|

|
Position du problème: entre deux rues à angle aigu, la direction de faîtage AB imposée
|

|
Le faîte est horizontal, donc les points A et B sont à la même hauteur. Au sommet du mur, comme cela se vérifie en observant le rang de briques, C et D ont aussi une hauteur commune (plus basse que la précédente). De cette configuration imposée, il résulte que
les droites AD et BC ne sont pas coplanaires
(un calcul facile le montre, mais nous laissons au lecteur le choix:
nous croire... ou prendre son crayon et faire ces 4 lignes
d'exercice...).
Or les poutres de la charpente doivent s'appuyer sur AD et BC, en restant dans des plans verticaux parallèles à celui du faîte.; cela définit exactement un P.H.!
Les lignes de tuiles reproduiront ces directions, ce qui permet de s'en rendre compte sur l'image cicontre, faute que le Mathouriste soit arrivé assez tôt, alors que la charpente était encore à nu.
Mais que dit le propriétaire, après avoir confirmé son peu d'accointance avec la noble science défendue dans ces pages?
"Mon père était charpentier, j'avais un peu de savoir-faire... mais quand même, le problème ne me paraissait pas évident; alors, j'ai fait une maquette! Elle m'a donné satisfaction, alors, je me suis lancé, et voilà."
Et voilà: bravo! L'auteur de ces lignes aura assez prêché
l'utilité des croquis à ses étudiants pour savourer cette réponse... en
3D.
|
En faire un toit? De quoi fasciner plus d'un architecte...
Les progrès dans la réalisation de coques minces en béton, conjugués à
la possibilité de coffrages simples grâce à la génération réglée, ont
permis des réalisations de très grande envergure. URSS et pays de l'Est
se sont montrés, en l'occurrence, moins frileux, moins traditionalistes
que la vieille Europe.
Selon les cas, la réalisation souligne davantage l'aspect de selle, en courbes, ou fait plutôt ressortir la génération réglée
Faire ressortir la selle.
 |
 |

|
Théâtre
d'été, Dniepropetrovsk (Ukraine)
le Mathouriste
remercie son étudiant Maxime Roetynck, auteur de
ces 2 clichés. |
stade de basket-ball à Wloclawek (Pologne)
architectes: W. Ryżyński, M. Sobisiak
|
Faire ressortit la génération réglée
Peut-être préférez-vous voir encore les génératrices une fois le
toit terminé? Alors, rendez-vous à Washington,
dans une église de quartier:
 |
 |
 |
|
St Augustine's Episcopal Church
(Washington, USA) |
|
La photo centrale met en
évidence le fait que les génératrices
sont toutes située dans des plans parallèles (en
l'espèce, verticaux, perpendiculaires aux murs).
Bien sûr, une plaque de zinc est un morceau de plan, et
aucune portion de plan n'est incluse dans un
paraboloïde hyperbolique. Mais l'approximation est excellente
-et l'intention, évidente.
Les images de détail soulignent le fait que le
paraboloïde hyperbolique est une surface gauche:
le long d'une génératrice
(matérialisée ici par une ligne de raccordement
des plaques de zinc), le plan tangent change constamment; il n'y a pas
deux points où il est le même.
 |
 |
| 600 M St SW,
Washington, DC 20024, à l'angle de Maine Avenue SW ( localiser
) |
À Varsovie, voici une gare (construite entre 1954 et 1962) dont le toit
est un voile de béton en P.H., mais la peinture en souligne
astucieusement la génération réglée.

|

|
| Gare Ochota, à Varsovie (Pologne) |
pour sauver l'honneur de la France...
Il y a, d'abord, un Suisse et un Grec... qui ont pris la nationalité française. En 1958, Iannis Xenakis
(célèbre comme musicien, mais dont il ne faut pas
oublier qu'il fut aussi architecte) utilisait cette surface qu'il
affectionne pour concevoir le Pavillon Philips de l'Expostion
Universelle de Bruxelles. Le
Corbusier,
auprès de qui il fit ses armes, ne
serait pas étranger à cette inspiration; d'ailleurs, l'intérêt de
"Corbu" pour les surfaces réglées apparait nettement dans notre page
Hyperboloïdes...( en apprendre plus sur la
carrière d'architecte de Xenakis et sa collaboration avec Le Corbusier)
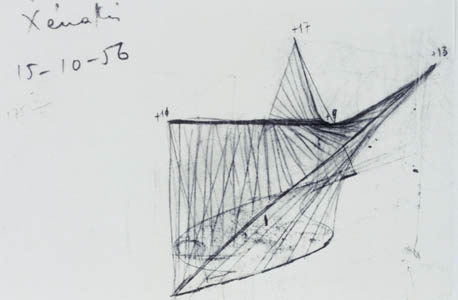
|

| 
|
Croquis de l'architecte
|
En chantier... | Achevé!
(source Wikipedia : très grande image)
|
Le bâtiment était composé de neuf
paraboloïdes hyperboliques assemblés entre eux (sur l'image agrandie, la génération réglée est bien en évidence), et,
à l'intérieur, on pouvait entendre le Poème
Électronique d'Edgar Varèse!
Assez stupidement, mais c'est souvent le sort de ces constructions
considérées comme éphémères, il n'a
malheureusement pas été conservé.
Quelques liens intéressants sur le sujet:
C'est, dit-on ce qui aurait inspiré cla gare Ochota de Varsovie...
|

|
Et puis, il y a le toit de remarquable cathédrale de Royan... Mais il
est si haut qu'on est réduit, faute de survol, à croire sur parole les
descriptifs (y compris à l'intérieur de l'église), car on ne le voit
pas de dedans: il est caché par un plan de béton.
Bien moins usuel: pour faire un mur!
Un joli site à Dresde...
Découverte au hasard d'une
promenade dans Dresde -il y a les bâtiments qu'on signale au
touriste dans tous les guides... et les autres, ceux que seules les
longues flâneries urbaines vous révèlent, les jours
de chance- la Nouvelle Synagogue a offert au
Mathouriste
l'incroyable surprise que voici: le paraboloïde hyperbolique a ici
toutes ses génératrices dans des plans horizontaux,
chaque ligne de la maçonnerie se décalant
légèrement par rapport à la
précédente.

|

|

|
| Vue du haut de la rue (1) |
Dresde (Allemagne): la Nouvelle Synagogue (2) |
Vue du bas de la rue (3) |
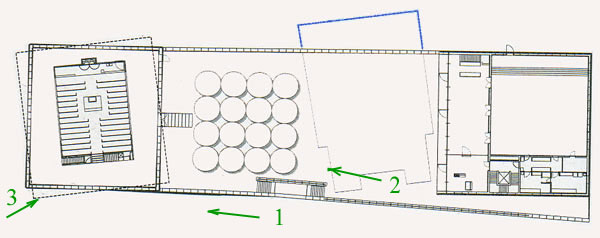 Plan de la Nouvelle Synagogue; tracé (bleu et pointillés) de l'ancienne
Plan de la Nouvelle Synagogue; tracé (bleu et pointillés) de l'ancienne
et localisation (approximative ) des points et angles des prises de vue ci-dessus.
Comme on le découvre sur ce
plan, ce bâtiment moderne (achevé en 2001) s'est
installé sur les fondations d'une
ancienne synagogue, conçue par l'architecte
Semper, édifiée en 1840, et incendiée par les nazis lors de la
nuit de Cristal, (9 au 10 novembre 1938).
Les ruines furent ensuite dynamitées, et une partie des pierres recyclée pour
la construction de routes.
L'architecture est due au cabinet Wandel, Lorch und Hirsch
(Saarbrücken), et le projet a fait partie
des 43 nominés pour le
Prix de l'Union Européenne pour l'Architecture Contemporaine 2003.
nte.

|

|

|
| Détail (3) |
Détail (1) |
Détail (2) |
La localiser.
... et deux à San Francisco!
Le
Mathouriste
ne s'attendait certes pas à retrouver cette rare disposition dans une
autre ville... encore moins à la trouver deux fois dans la même, mais
rien n'est impossible en Amérique, comme le remarquait déjà Jules
Verne. Et encore moins en Californie, encore moins à San Francisco.
Commençons par la "tour" (dite tour Hamon, hauteur 44m) du
Musée De Young (2005, architectes:
Herzog & de Meuron , Bâle):
Rendons-nous maintenant à la cathédrale de la ville, Sainte Marie de
l'Assomption. La hardiesse architecturale concerne bien le toit, mais,
contrairement à tous ceux rencontrés jusqu'ici, celui-ci n'est pas une
selle "à l'horizontale", comme on la disposerait sur un cheval. Il y a
huit P.H., qui ont pour mission de
réaliser la transition fluide entre une croix et un carré, et donc disposés "à la verticale", exactement comme dans le musée De Young..

|

|
Vue générale (de côté)
|
Face à l'entrée |
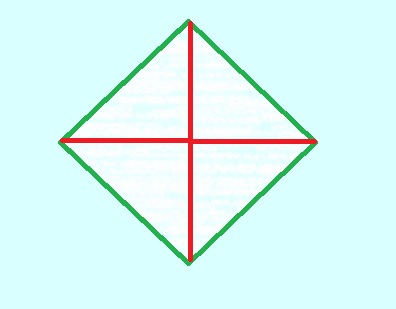
En effet, la partie la plus haute de l'église constitue une croix
horizontale, que nous avons matérialisé ci-dessous en rouge. Projetée
sur le plan que suggère le haut des murs (partiellement réalisé par une
dalle en béton, mais dont on découvrira à l'intérieur qu'elle est
évidée pour ne rien perdre de l'élégance de ce clocher), elle constitue
les diagonales d'un carré (vert), dont chaque sommet est le pied d'une
verticale matérialisée par une mince colonne de vitrail. La croix et le
carré sont donc dans des plans horizontaux séparés par la hauteur des
minces colonnes de vitraux.
Joindre une branche de la croix à un demi-côté du carré (à l'évidence, non coplanaires) se fait par un P.H. dont certaines génératrices apparaissent clairement sur le béton. Ce qui en fait bien huit en tout!
|

|
| La croix (niveau haut) et le carré (niveau bas) |
placés sur le monument
|
On saisira
bien plus facilement les 8 P.H. par le regard en entrant dans l'édifice et
en les regardant par en dessous.
Sur l'imagette la plus à droite nous avons tracé dans les mêmes
couleurs, en rouge et en vert, les portions de droites servant de
directrices à l'une de ces surfaces.
Au cas où vous douteriez encore, la
page Wikipedia consacrée à cette église vous confirmera la présence de ces huit P.H. Vous y apprendrez aussi qu'elle a été conçue par les architectes
Pier Luigi Nervi et
Pietro Belluschi, qu'elle a été achevée en 1971, et qu'elle est considérée comme
une des dix plus belles églises des USA;
Mais elle abrite encore d'autres P.H., un peu plus discrets, à la base
de chacun de ses piliers. Sur l'imagette de droite, nous avons montré,
en rouge et vert, les deux droites directrices non coplanaires, sur
lesquelles s'appuient toutes les génératrices, dont quelques unes ont
été soulignées en jaune; mais elles sont faciles à voir, puisqu'elles
suivent les traces... des planches de coffrage!
Et avec des fils?
Les mathématiciens sonr coutumiers des maquettes en fils pour les
surfaces réglées: elles illustrent très concrètement la génération par
droites, tout en donnant une bonne idée de la surface quand le réseau
est assez dense. Mais il est possible de rencontrer des réalisations
plus grandioses... témoin ce pont, à Rotterdam.

|

| 
|
Croquis de l'architecte
|
En chantier... |
|
Les câbles sont des droites, dont les points d'ancrage se situent sur
deux droites horizontales non coplanaires (un côté du tablier, et dans
une direction perpendiculaire en haut du portique. Grâce à l'intervalle
fixe entre deux ancrages successifs, il s'agit bien d'un P.H. (le
lecteur curieux et sachant former l'équation d'une droite dans l'espace
le vérifiera aisément).
C'est exactement le même scénario: fils s'appuyant sur deux
horizontales, perpendiculaires et à des niveaux différents, qu'on
découvrira comme "écrin" de présentation du modèle de fusée imaginé par
le grand pionnier russe de la conquête spatiale,
Konstantin
Tsiolkovski. C'est à voir dans le
musée qui porte son nom, dans sa
ville natale, Kalouga (Russie). Il y a même DEUX P.H, car on y a
exploité deux côtés d'un carré au sol, et deux côtés d'un carrré au
plafond.

|

|

|

|
Autour de la maquette inspirée par les dessins de Tsiolkovski (musée de Kalouga)
|
Plus surprenant... où les fils sont remplacés par des tuyaux!

|

| 
|
En se promenant le long de la Coulée Verte, à Paris.
|
Les génératrices (épaissies en tuyaux de cheminées...) sont situées
dans des plans verticaux parallèles, et s'appuient sur deux droites à
l'évidence non coplanaires (la sortie de toit de la maison concernée
d'une part, la droite de rencontre avec le haut mur vertical, d'autre
part); c'est une fois de plus, la définition réglée de la surface.
Place aux Artistes!

|
Ces deux tableaux étaient présentés à la rétrospective consacrée à Martial Raysse
par le Centre Pompidou en 2014. Inspirés à l'artiste par une photo de
son épouse, France, ils se préteraient fort bien à un jeu des 7
erreurs... qu'est-ce qui les distingue le plus? De fins connaisseurs
répondraient sans doute que celui de gauche avait appartenu au
président Pompidou. (Les deu sont aujourd"hui propriétés du musée).
Mais pour le géomètre... la toile de gauche est
plane, tandis que celle de droite est... un
paraboloïde hyperbolique, ou, du moins, l'approche.
Certes, au sens strict, une pièce de toile, plane, ne peut être
appliquée sur un P.H. (au contraire d'un cône ou d'un cylindre,
dénommés pour cette raison surfaces développables). Mais une certaine
élasticité de la toile autorise ce léger gauchissement. Les deux bords
verticaux sont les droites d'appui (à l'évidence non coplanaires), et
si l'on regarde la toile comme une réunion de fils horizontaux
s'appuyant sur ces deux droites, on retrouve bien la définition réglée
du P.H.
On remarquera l'humour de l'artiste, qui pousse la provocation jusqu'à
qualifier de convexe, dans son titre, une surface qui ne l'est
certainement pas!
|
À gauche: Tableau dans le Style Français II (1966)
À droitee: Tableau métallique- Portrait à Géométrie Convexe (1964)
Le vues de côté montrent clairement le support en P.H. de la seconde.
|

|

|
|
Par contraste, le peintre suivant
(nettement plus ancien, et plus académique...) n'avait sans doute
aucune intention géométrique... mais en représentant une machine à mâter
(poser un mat sur un bateau en construction), il a représenté deux axes
non coplanaires (le mât en cours d'installation, et celui, verticalde
la machine)... certes, il n'y a que 3 droites en appui dessus, mais ne
voit-on pas facilement un P.H. en les imaginant, glissant d'un
mouvement continu de l'une à l'autre? C'est la génération rectiligne en
action!

|

|
Vue du Port de Rochefort, par Antoine-Léon Morel-Fatio (1810-1871)
Me sujet principal est la machine à mâter.
|
Détail du tableau
(en luminosité augmentée)
|
Quand deux P.H. se rencontrent...

|

|
...C'est à Tromsö (Norvège). Ce
bâtiment , aujourd'hui une bibliothèque, a été réaménagé en 2005 en
réhabilitant l'ancien cinéma Focus, conçu par l'architecte Gunnar
Böberg Haugen, inauguré le 16 Mars 1973. Seul le toit a été conservé,
cette coque mince en béton étant apparue ne parfait état. Elle couvre
une surface de 3710m² , sa base étant un carré d'environ 60m de côté.
Bâtie sur un modèle abondamment utilisé, sous diverses variantes, par
l'architecte mexicain Felix Candela, la voûte est constituée de deux
paraboloïdes hyperboliques identiques, le deuxième étant déduit du
premier par une rotation de 90° .
|
|
|
|
|
Les deux P.H. se coupent
suivant deux sections planes paraboliques; les images ci-contre -qui ne
peuvent bien sûr en faire voir qu'une- mettent bien en évidence le fait
qu'il s'agit d'une courbe plane. On peut le montrer facilement:
Le petit coin de la technique: (des calculs à lire ... ou à sauter!)
Avec un axe des sz orienté vers le haut, un des P.H peut être représenté par une équation du type
z = x² - a²y²
avec a>1 (par exemple, a
= 2 ou 3) La valeur exacte ne nous est pas connue, mais elle n'a rien
d'essentiel; on observe juste ici que la parabole de façade (concavité
vers le bas) est plus resserrée que celle des lignes de faîte.
L'autre est, par symétrie
z = y² - a²x²
si bien que l'intersection est donnée par
z = x² - a²y² = y² - a²x²
soit
x² = y² ; z = x² - a²y²
i.e.
x = y ; z = (1 - a² ) x² ou x = - y ; z = (1 - a² ) x²
Une rotation de 45° du repère fournirait l'aquation de la parabole dans son plan, "en vraie grandeur".
|
|
 |
 |
À consulter en complément: (en Italien, mais avec de nombreuses images, exemple ci-contre)
Voir comme exemples une église en Espagne, et un restaurant au
Mexique
sur cette
page de R. Ferréol.
|
|
Pour en savoir plus mathématiquement...
Vers
les autres sections: