Omar KHAYYAM
du Troisième Degré au Septième Ciel...
#2 : le Traité sur la Division du Quart de Cercle
( l'Artisan, le Triangle et le Mathématicien )
Curieux ouvrage, au premier abord:
Que le lecteur se rassure: il n'est pas indispensable de suivre l'ordre chronologique d'écriture; et il peut tout aussi bien lire d'abord la page consacrée au Traité des Équations Cubiques avant de revenir à celle-ci pour essayer d'approfondir la motivation de l'auteur. |
 |
Un début mystérieux
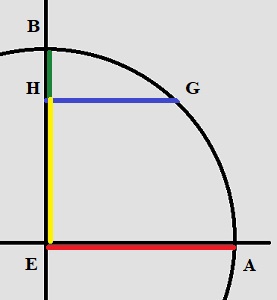 |
"Nous voulons diviser le quart AB d'un cercle ABCD en deux parties au point G, et mener la perpendiculaire GH au diamètre BD, telle que le rapport de AE à GH soit égal au rapport de EH à HB; E est le centre du cercle, et AE le demi-diamètre."
O. K. , Traité sur la Division du Quart de Cercle
|
Voilà la toute première phrase de ce traité: difficle d'être plus mystérieux! Pourquoi résoudre cette question particulièrement? Quelle en est l'utilité? A-t-elle une source remarquable, antérieure ou non à Khayyam? Aucune réponse à ces questions, ni dans le traité lui-même, ni chez les commentateurs ultérieurs. Nous avons, dans notre page biographique, cité une possible motivation par les pratiques artisanales: cela se tient, mais aucune preuve ne vient soutenir cette proposition. |
Une première Analyse
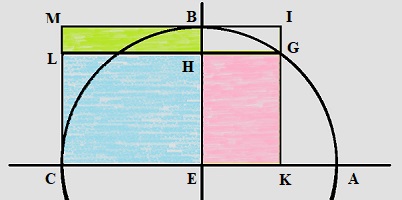
Supposant G connu rélaisant cette division, Khayyam complète sa figure en portant sur la tangente en B, BM=AE à gauche du rayon EB, et BI=HG à droite, pour traduire l'égalité des deux rapports en égalité de deux produits, qu'il interprète comme l'égalité des aires de deux rectangles.Khayyam a certes fait intervenir une hyperbole, mais son asymptote verticale , connue en phase d'Analyse, est inconnue en synthèse, puisque c'est la verticale de G. D'où la nécessité de reposer différemmment la question.
Toutefois, un point demeure extrêmemnt surprenant: si, au lieu de compléter les aires vertes et roses par le rectangle jaune BIHG, Khayyam avait utilisé le rectangle (bleu, sur la figure ci-contre) LHCE, il aurait placé le point G sur la même hyperbole d'asymptotes fixes CM et CA que le point B... et c'était fini, plaçant G à l'intersection d'un cercle et d'une hyperbole entièrement déterminés. Comment n'a-t-il pas pu voir cela?
Quoi qu'il en soit, il va se lancer dans une nouvelle analyse, qui va introduire son fameux triangle. |
 |
Deuxième Analyse... Naissance d'un Triangle
Quoi q
 |
"Je
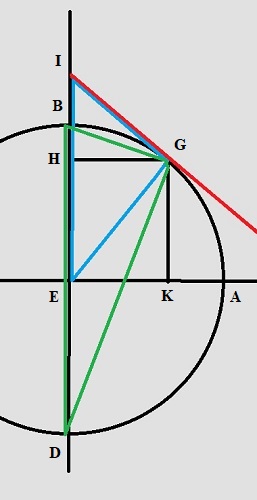
dis, avec l'aide de Dieu: nous retraçons la figure, en supposant par
l'analyse que nous avons fait ce que nous voulions: que le rapport de
AE à GH soit égal au rapport de EH à HB; Menons du point G la tangente au cercle. Prolongeons EB jusqu'à ce qu'elle coupe la tangente au point I, et joignons GE. "
O. K. , Traité sur la Division du Quart de Cercle
|
Voilà la toute première phrase de ce traité: difficle d'être plus mystérieux! Pourquoi résoudre cette question particulièrement? Quelle en est l'utilité? A-t-elle une source remarquable, antérieure ou non à Khayyam? Aucune réponse à ces questions, ni dans le traité lui-même, ni chez les commentateurs ultérieurs. Nous avons, dans notre page biographique, cité une possible motivation par les pratiques artisanales: cela se tient, mais aucune preuve ne vient soutenir cette proposition. |
"
Les grandeurs sont les quantités continues, qui sont quatre: la ligne,
la surface, le corps et le temps, comme on le trouve exposé d'une
manière globale dans les Catégories [d'Aristote]. [...]
Il n'est pas d'usage de de mentionner le temps au nombre des sujets des
problèmes de l'algèbre; mais si on l'avait fait, ç'eût été légitime. Il
est de coutume, chez les algébristes, de nommer dans leur art
l'inconnue qu'on veut déterminer «chose», son produit par elle-même «carré», son produit par son carré, «cube», le produit de son carré par son semblable «carré-carré», le produit de son cube par son carré «carré-cube», le produit de son cube par son semblable «cubo-cube», et ainsi de suite aussi loin qu'on veut."
O. K. , Traité d'Algèbre
|
CHANTIER en travaux!
Revenez bientôt... |