La dédicace
au calife Al Ma'moun est le seul élément qui permet de
le dater, entre 813 et 833; elle précise aussi qu'il s'agit
d'une commande "utilitaire", souhaitée par le souverain pour
venir en aide à ses sujets dans les questions pratiques de la
vie sociale:
"C'est ce
par quoi Dieu a
distingué le guide Al
Ma'moun, le Commandeur des Croyants (...) qui m'a encouragé
à rendre plus clair ce qui était obscur et à
faciliter ce qui était difficile"
"J'ai rédigé sur
le Calcul par
la Restauration et la Comparaison un livre abrégé,
englobant (...) ce
dont ont besoin les gens dans leurs héritages, dans leur
donations, dans leurs partages, dans leurs jugements, dans leur
commerce et dans toutes ls transactions qu'il y a entre eux à
propos de l'arpentage des terres, du creusement des canaux, de la
géométrie et d'autres choses."
Les Deux Techniques Fondamentales
Dans un souci de clarté, nous les présentons en notation
moderne. On verra ensuite la version historique...
Leur but est de ramener les équations à un type
canonique, à partir duquel on lancera l'algorithme de calcul des
solutions.
Voici une équation telle qu'un
problème de géométrie peut nous en
délivrer, sous forme brute:
x² + ( 10 -
x)² = 58
2 x² + 100 - 20 x
= 58
Jabr:
C'est l'opération qui consiste à se débarasser des
termes négatifs, en les
faisant passer
de l'autre côté de l'équation.
On réécrit donc l'exemple précédent en
2 x² + 100 = 20 x
+ 58
Le mot
Jabr évoque la
réduction, jusqu' au sens chirugical "réduire une
fracture" (qu'il possède en langue Arabe): s'il y avait
déjà
10 x (par
exemple) au second membre, on réduirait le terme à
20 x + 10 x = 30 x.
Muquabala:
C'est l'opération de
réduction
des termes semblables de part et d'autre de l'équation.
Ici, 100 = 58 + 42, on peut donc enlever 58 des deux côtés
sans rien changer.
2 x² + 42 = 20 x
Muquabala
évoque l'idée
de balance, de justice: enlever 58 unités de poids sur les deux
plateaux d'une balance ne modifie pas l'équilibre!
On complète par une division
par 2, car, pour toutes les équations possédant des
termes des trois sortes (
x²,
x , constante ), Al-Khowarizmi se
ramène toujours au cas où le coefficient dominant
de
x² est 1.
x² + 21 = 10x
Les 6 Types Canoniques
Nous n'en avons aujourd'hui qu'un seul:
a x² + b x + c = 0
parce que nous ne ressentons aucune
gêne à manipuler les coefficients négatifs. Il n'en
est pas de même à l'époque: ils ne semblent pas du
tout naturels, ils sont "trop abstraits"! De même, les solutions
doivent correspondre à des sommes d'argent, à des
longueurs...
elles ne "peuvent" donc qu'être positives eu égard
à la nature des problèmes posés et aux solutions
attendues.
Les six types proposés par le Traité sont, dans cet ordre:
a x² = b x (1)
a x² = c (2)
a x = c (3)
x² + b x = c (4)
x² + c = b x (5)
b x
+ c
= x² (6)
L'Algorithme de Résolution
Un peu du Vocabulaire du Maître...
Pour comprendre le texte historique, un lexique préliminaire est
nécessaire; l'auteur nous le présente lui-même:
"J'ai découvert aussi
que les nombres dont on a besoin dans le calcul du jabr et
de la
muqâbala sont de trois sortes: ce sont les racines, les
biens et le nombre seul, non rapporté à une racine ou un
bien."
racine <-------------> x
bien <-------------> x²
nombre
<--------------> 1
Plus
exactement, il appelle ainsi les coefficients de ces
quantités... puisqu'elles ne seront jamais écrites,
contrairement à notre habitude "moderne". Une habitude
inaugurée par
François
Viète (1540-1603) seulement en ...1591!
L'équation de notre exemple (en fait, le sien) :
x² + 21 = 10x
se lit ainsi:
"un
bien et
vingt-et-un dirhams
égalent dix racines"
La quantité connue, le "nombre seul" est exprimée
par une unité monétaire, le
dirham
(l'origine du mot est
à chercher dans le Grec
drachme,
il désigne toujours une telle unité aujourd'hui dans de
nombreux pays arabes) : sans doute faut-il y voir l'origine
concrète de certains problèmes... mais aussi une forme
d'abstraction, car le mot reste employé, même s'il ne
s'agit pas d'un problème financier!
L'objet inconnu "naturel" semble être, à travers la
dénomination, le bien (
x² ),
plutôt que la racine (
x ). Cela
semble provenir de la tradition Babylonienne: dans un problème
d'héritage, on cherche à répartir un
bien -au sens notarial du mot!-, qui
est une
surface, dont on
recherchera pour les calculs la
racine
(la longueur du côté du carré qui lui correspond).
La richesse se mesure en surface (cultivable, par exemple), pas en
longueurs!
En suivant pas à pas...
La méthode est donnée sur les exemples, mais de
façon à faire clairement sentir sa
généralité: celle-ci est clairement
exprimée
(déférence gardée envers le Créateur...)
dans le commentaire qui suit
la résolution de l'exemple
x² + 10 x = 56
(4)
"Procède ainsi avec tous les
biens et toutes les racines et ce qui leur est égal en nombre,
et tu réussiras si Dieu le veut."
Il n'est pas inintéressant
d'observer que cette démarche, peu pratiquée dans les
cours de Mathématiques, reste tout à fait naturelle dans
les cours d'Informatique où les meilleurs auteurs
présentent
ainsi leurs
Algorithmes, en
faisant "sentir ce qui est général sur l'exemple choisi":
algorithme du simplexe, de plus courts chemins sont des exemples de
choix. Ce qui n'entame aucunement la rigueur et l'exigence
démonstrative, voir l'ouvrage [CLR], particulièrement
chéri du Mathouriste...
Revenons au traitement par Al-Khowarizmi de l'exemple:
x² + 21 = 10x
qui est du
type
x² + c = b x (5)
"Divise
en deux les racines, ce qui donne
5;"...
[
calcule
-b/2 ]
... "multiplie 5 par
lui-même:
tu obtiens 25; "...
[ élève au carré
b²/4 ]
..."retire les 21 qui sont
ajoutés au carré: il reste 4;"...
[ retranche
c
:
b²/4 - c
] ça y est, on tient le discriminant D
(divisé par 4) !
..."extrais la racine -cela
donne 2-"...
[
d = Sqrt (
D ) ]
..."et retire la de la
moitié des racines, c'est à dire de 5: il reste 3; c'est
la racine que tu cherches."
[ x =
b/2
-
d
]
c'est notre formule moderne, pour un coefficient dominant égal
à 1.
Cela est décrit pas à pas, cela
permet de faire très
sûrement à quelqu'un qui
ne
sait pas pourquoi il fait , bref cela lui permet de se comporter
comme une machine... à qui nous ne disons rien de plus, lorsque
nous programmons une formule de résolution. L'
algorithme, au
sens "
description
méthodique de la suite des opérations à effectuer",
est bel et bien né! Et l'algorithme
précède
la formalisation de l'écriture de l'équation, car il ne
nécessite pas l'invention des symboles d'inconnue, de
carré, etc...
Quelques Remarques Complémentaires...
1. Le
procédé pratique (
"ce
dont ont besoin les gens" ) précède
la justification; mais, rigueur oblige, celle-ci suivra, avec une
exigence et une manière toutes géométriques, en
s'appuyant sur les
Eléments
d'Euclide.
2. Un
"petit ennui" n'aura pas échappé au lecteur
moderne: x =
b/2
- d ou x =
b/2 + d ?
Mais il n'a pas échappé à l'auteur non plus:
" Si
tu rencontres un
problème qui se ramène à ce cas [i.e.
(5)],
examine
alors sa justesse à l'aide de l'addition; si tu ne le peux, tu
obtiendras certainement la solution à l'aide de la soustraction.
Parmi les trois
cas où l'on doit
diviser en deux la racine [i.e.
(4) à
(6)
; il désigne ici le début du calcul du
discriminant] ,
c'est le seul
où l'on se serve de l'addition et de la soustraction."
Effectivement, pour (4) et
(6)
, le produit des racines est -c
négatif ( en vision moderne ); pour Al-Khowarizmi le
problème n'a qu'une solution, celle qui est positive. En outre,
sa façon de dire ( "tu obtiendras certainement la solution" )
suggère que le problème pratique posé ne saurait
avoir plus d'une solution; très certainement, son contexte doit
faire apparaitre une condition de domaine pour l'inconnue, issue
du bon sens, de limites effectives, d'intégrité...
3. Un
point non éclairci demeure autour des solutions
négatives: elles ont été employées sans
hésitation par le mathématicien Indien Brahmagupta
(598-670), qui disposait de formules de résolution analogues.
Or,
Al-Khowarizmi connaissait certains ouvrages de Brahmagupta:
ses tables astronomiques sont largement inspirées de celles de
l'Indien. Son
Livre
sur le Calcul Indien rend tribut à l'Inde pour le
système positionnel de numération. Par contre, aucune
influence n'est déclarée pour le traité
d'Algèbre, et soit il n'a pas eu connaissance des solutions
négatives, soit il les a rejetées comme innaceptables.
4. Une équation du
second degré, ça se discute sur son discriminant, c'est
bien connu...et d'Al-Khowarizmi en premier
lieu; en cela il surclasse nettement Brahmagupta qui
n'aborde pas ce point
:
" Sache en
outre
que dans ce cas [i.e. (5)],
si tu divises
en deux
la racine, que tu
la multiplies par elle-même et que le produit est plus petit que
les dirhams qui sont ajoutés au carré"...
[ b²/4 < c ou encore D =
b²/4 -c < 0 ]
"alors
le problème est impossible."
Et ce n'est pas tout;
il poursuit:
"Mais s'il est égal aux
dirhams"...
[ b²/4 = c ou encore D =
b²/4 -c = 0 ]
"la
racine carrée est égale à la moitié de la
racine."
[ x =
b/2 ]
autrement dit, le cas de la racine double est parfaitement
identifié comme tel.
Justifications
Géométriques
Al-Khowarizmi donne la
démonstration géométrique suivante pour
l'équation:
x² + 10 x = 39
(4)
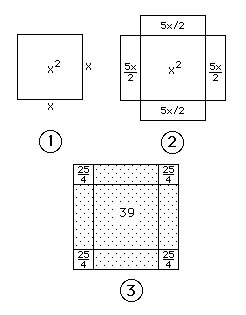
figure
issue de cette
page (Université de Saint-Andrews, Ecosse)
- L'inconnue (le bien!) est
l'aire x² d'un
carré de côté x.
- On peut construire sur
chacun des côtés de ce carré un rectangle dont un
côté est x, et l'autre
5/2: ainsi l'aire totale de ces 4 rectangles représente le terme
10 x;
l'aire totale représentée est x² + b x = c .
- Ainsi, il manque, pour
obtenir un carré, 4 petits carrés de côté
5/2 [ et, de façon générale, 4 . (-b/4)² = b²/4 ]. Alors, le carré de
côté (x + 2.b/4) = (x
+ b/2) aura pour aire 39 + 25
= 64 [ et, de façon
générale, D = c
+ b²/4 ]
- Conclusion: (x
+ b/2)² = D, d'où la formule de
résolution!
Tout
ceci revient de manière limpide à notre actuelle mise
sous forme canonique, dont le but n'est autre que de se ramener
à l'équation
x² = D
(2)
dont cela constitue la visualisation
géométrique!
Le texte
authentique figure en traduction dans [
DJ2].
Il donne d'ailleurs une deuxième construction, n'utilisant plus
cette fois que deux rectangles
dont
un
côté est x, et l'autre b/2. C'est encore plus naturel pour
figurer
(x
+ b/2)² = D
Saurez vous la restituer? [
Solution en couleur sur cette
page ]
Désormais, il n'y aura plus qu'une figure par preuve. Celle de
l'exemple x² + 21 = 10x
choisi pour étudier l'algorithme est dans [MAH].
Quelques documents
complémentaires au fil du Web:
- DOC
1 en Français, DOC 2 et DOC
3 en
Anglais.
- DOC
4: Geometric Approaches to Quadratic Equations from Other Times and
Other Places (P.ALLAIRE, R. BRADLEY) sur la vision
géométrique des problèmes du second degré
à travers l'Histoire (en
Anglais)
- DOC 5 sur les traductions et/ou altérations
du texte original.
- et ... une partie d'une
présentation-diapos animée These
Are A Few of My Favourite Things,
titre cher au Mathouriste pour l'accompagnement musical auquel il
invite
(John Coltrane Quartet, Live in Europe 1963, Afro Blue Impressions): La Mélodie du
Bonheur... des
équations quadratiques!
Exemples de Problèmes
[ très
prochainement !!! ]
Le Plan du Livre
Première
Partie
- Chapitre 1 :
- Le Système Décimal Indien, la Numération
de Position
- Les Objets de l'Algèbre: le Nombre, la Racine et le Bien
- Les Six Types d'Equations
- Chapitre
2 :
- Procédés de Résolution pour Chacun des
Types Précédents
- Justifications Géométriques
- Chapitre 3 :
- Comment Poser les Problèmes et les Ramener aux Six
Types d'Equations
- Chapitre 4
:
- Extension des Opérations Arithmétiques aux
Expressions Algébriques
- Règle des Signes: Enoncé sans Justification
- Chapitre 5
:
Deuxième
Partie
- Chapitre 6 : Applications
- Transactions Commerciales
- Arpentage
- Répartition des Héritages.
Bibliographie
- [CHA] J-L. CHABERT & alias,
Histoire d'Algorithmes (Belin)
- [CLR] T. CORMEN, C. LEISERSON, R. RIVEST, Introduction à l'Algorithmique
(Dunod)
- [DJ1] A. DJEBBAR, Une Histoire
de la Science Arabe (Points-Sciences)
- [DJ2] A. DJEBBAR, L’Algèbre Arabe. Genèse d’un
art (Vuibert)
- [DJ3] A. DJEBBAR, Le Nombre, la
Racine et le Bien in L'Origine
des Equations (Cahiers de Sciences & Vie, n°56, Avril
2000)
- [MAH] N. MAHAMMED, Sur la
Résolution des Equations Algébriques (Diderot)
- [MON] E. MONNIER,
L'Apogée des Sciences Arabes in Le Génie Arabe, Enquête sur
les Secrets d'un Age d'Or (Cahiers de Sciences & Vie,
n°71, Octobre 2002)
- [RA2] R. RASHED, Histoire des
Sciences Arabes, t2: Mathématiques et Physique (Seuil)

In Memoriam:
Le
Mathouriste
dédie cette page à la mémoire de son
collègue et ami Norreddine Mahammed (1944-1994),
enseignant-chercheur à l'Université Lille-I (1969-1992),
puis professeur à l'Université du Littoral à
Calais, qui, le premier, l'a initié aux beautés de l'
al-Jabr
et de la
Muqabala.
