La Chaînette
(sur un rythme Américain)
Saint Louis Blues, quoique...
Saint-Louis
(Missouri),une fin d'après midi. Peut-on se promener dans
les rues, sur le Mississipi, sans se fredonner le plus grand "tube" de
W.C. Handy?
Sans une
pensée pour l'immortelle
version (1925) de Bessie Smith avec son contre-chant de
cornet -pas encore la trompette!- de Louis Armstrong?
Statue de W.C. Handy dans Beale Street, Memphis (Tennessee)
Statue de W.C. Handy dans Beale Street, Memphis (Tennessee)
Pour vous aider
à vous mettre dans l'ambiance, un extrait du
film Saint-Louis Blues,
avec la grande Bessie, (1929), et un extrait
de concert de Louis (Belgique,1959). Vous voilà
prêt maintenant à faire un peu de
mathématiques! Avez vous bien entendu le tout premier vers:
"I hate to see dat evening sun
go down..."
Est-ce bien ce que l'on a envie de se dire, tant on a peine, d'où qu'on regarde, à détacher son regard de la Gateway Arch du Jefferson National Expansion Memorial ...
Est-ce bien ce que l'on a envie de se dire, tant on a peine, d'où qu'on regarde, à détacher son regard de la Gateway Arch du Jefferson National Expansion Memorial ...
 |
 |
 |
Elle est
l'œuvre de l'architecte Américain (d'origine
Finlandaise) Eero
Saarinen (1910-1961).
La scuplture qui lui rend hommage, ainsi qu'à ses collaborateurs, à l'intérieur du monument, livre la clé de l'idée... avec la complicité du dispositif d'organisation des files d'attente pour la visite! Celles-ci sont délimitées par des chaînes; chacune d'entre elles, fixée à deux piquets, se "laisse aller" à sa forme d'équilibre sous l'action de la pesanteur. Saarinen, qui aimait cette forme pour sa beauté et son caractère mathématique simple, songea alors à l'inverser, pour créer une structure qui ne serait soumise, sous l'action de son poids, qu'à un effort de compression, sans cisaillement. Quelque chose d'aussi naturel, si l'on veut, que la forme d'une chaîne pesante suspendue par deux points.
Ce principe est repris par Bernard Forest de Bélidor (1698-1761), ingénieur militaire Français, dans un traité publié en 1725.
On y trouve au Livre II, De la Mécanique des Voûtes :
sous le titre: les remarques suivantes:
Certes, comme nous le verrons bientôt, la
solution
mathématique était trouvée, mais il
n'est pas
évident que Bélidor en était averti:
alors qu'il
soulignait dans son livre l'intérêt pour les
ingénieurs d'être rompus à
l'Algèbre, et en
usait abondamment, il ne donnait pour tracer cette courbe que l'usage
d'une ficelle!
On retrouve la courbe caténaire dans les croquis de Christopher Wren pour la construction du dôme de la cathédrale Saint-Paul de Londres ( étude: 1669 ; inauguration : 1708. La solution mathématique interviendra entre les deux dates!). On sait que Wren et Hooke se sont fréquentés et ont échangé des idées; Wren devait être bien informé du principe énoncé par Hooke. Lorsqu'il s'agit d'effectuer une vérification statique de l'équilibre du dôme de Saint-Pierre de Rome (construite en 1626) , Giovanni Poleni utilise lui aussi cette courbe dans ses figures (1748), ainsi que le principe de Hooke.
D'autres occasions se présentent de rencontrer cette question lorsqu'on visite les États-Unis, à preuve ces deux exemples ...
Mais, comme on l'a vu, les Européens y ont été confrontés bien avant. Leibniz, en préliminaire à sa résolution, en souligne l'intérêt (les constructions auxquelles il fait allusion sont celles des courbes, et non celle des bâtiments.)
Nous avons mis en gras les expressions qui semblent l'innocenter de l'erreur de jugement qu'on lui reproche habituellement, peut-être en raison d'une lecture un peu hâtive de Leibniz. Lequel poursuit son historique du problème en mentionnant celui qui trancha en 1627 la conjecture qu'il prêtait à Galilée: "Joachim Jung, éminent Philosophe et Mathématicien de ce siècle [...] se lança dans les calculs, fit des expériences, et disqualifia la parabole, mais sans lui substituer la véritable courbe."
L'Histoire a des manières amusantes de se répéter:
* Saarinen avait initialement pensé, lui aussi, à construire une arche parabolique... avant d'opter pour une forme mécaniquement plus naturelle.
* Et, c'est encore plus drôle, des commentateurs mal avisés de son œuvre y virent l'écho des arches du grand pont sur le Mississippi . Or, pas de chance, une arche de pont est le plus souvent parabolique. Un argument heuristique simple est le suivant, dont le principe mécanique est le même, mais dans l'ordre inverse, que celui formulé par Hooke: les cables d'un pont suspendu prennent naturellement la forme, non d'une chaînette (comme le fil qui pend sous son seul poids propre... ) mais d'une parabole, car ils sont soumis au poids du tablier (leur poids propre étant négligeable). Inversons maintenant le soutien, la meilleure répartition des efforts se fera suivant une parabole!
Poursuivant la tradition des défis entre savants,c'est ainsi qu'il lance un petit concours dans les Acta Eruditorum, qu'il anime.
Il n'a pas caché à ses correspondants qu'il détient la solution pour les faire saliver... et cela semble produire l'effet attendu:
À la fin de l'année 1690, il fait paraître les trois solutions correctes, dûes à Johann Bernoulli, Huyghens et lui même:
;
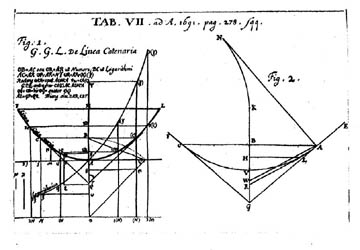
Figure illustrant l'article de Leibniz: construction de la chaînette
Route 66 Hall of Fame, Pontiac (Illinois)
Aujourd'hui, certains chercheurs pensent que des voûtes ou dômes qu'ils ont d'abord considérées comme paraboliques seraient, en fait, plutôt du type caténaire... L'argument en faveur de cette thèse serait celui du meilleur équilibre naturel de la structure -l'argument de Hooke, en somme, appliqué intuitivement par les bâtisseurs. Cela concerne, par exemple, les igloos des Esquimaux Canadiens, les huttes traditionnelles en boue séchée des Musgum au Cameroun,
Cela concerne d'abord celle qui, architecturalement, est la mère de toutes les voûtes en arc, la magnifique arche de Ctésiphon (Irak). Bien des ouvrages la mentionnent comme parabolique, mais ne nous y trompons pas: il s'agit dune allusion à la forme générale, pas le résultat d'une étude numérique précise. Au coup d'œil général, en somme... Et puis, il y a toutes celles que des architectes du XXème siècle ont réalisé en béton, grâce aux nouvelles possibilités d'un matériau qui les libérait des contraintes traditionnelles.
Le Mathouriste , qui ne dispose pas d'éléments assez précis pour trancher, vous les présente pour l'instant, avec plus de détails, dans sa page sur les cylindres paraboliques, en compagnie des cylindres elliptiques, sur lesquels des mesures soignées ont établi, justement, la difficulté de reconstituer avec certitude la nature des courbes directrices employées... Peut-être certaines changeront-elles de page, un de ces jours?
La scuplture qui lui rend hommage, ainsi qu'à ses collaborateurs, à l'intérieur du monument, livre la clé de l'idée... avec la complicité du dispositif d'organisation des files d'attente pour la visite! Celles-ci sont délimitées par des chaînes; chacune d'entre elles, fixée à deux piquets, se "laisse aller" à sa forme d'équilibre sous l'action de la pesanteur. Saarinen, qui aimait cette forme pour sa beauté et son caractère mathématique simple, songea alors à l'inverser, pour créer une structure qui ne serait soumise, sous l'action de son poids, qu'à un effort de compression, sans cisaillement. Quelque chose d'aussi naturel, si l'on veut, que la forme d'une chaîne pesante suspendue par deux points.
Un Peu de Statique (plus ou moins) Empirique...
Au demeurant, cette remarque simple n'était pas nouvelle; le premier à l'expliciter fut Robert Hooke (1635-1703), en 1675:| "Ut pendit continuum flexile, sic
stabit contiguum rigidum inversum." que l'on pourrait traduire approximativement par "De la même façon que pend un fil flexible, s'élève l'arche rigide, mais de manière inversée." |
Ce principe est repris par Bernard Forest de Bélidor (1698-1761), ingénieur militaire Français, dans un traité publié en 1725.
 |
 |
| Page de titre | Planche de figures de l'ouvrage. On reconnait, en bas, à gauche, la chaînette et la courbe inversée. |
On y trouve au Livre II, De la Mécanique des Voûtes :
| "PROBLÈME : Trouver quelle est la courbe qu'il conviendroit
de
donner à une Voûte, pour que tous les voussoirs,
étant égaux en pesanteur, soient en
équilibre?" "Si
[...], à deux points C et D, [...], l'on attache les
extrémités d'une chaîne
composée de petits
couplets & qu'on leur laisse la liberté de prendre
la
situation qui leur convient, je dis qu'ils composernot tous ensemble
une courbe CFD, dont la figure représente celle qu'il faut
donner à une Voûte, pour que tous les voussoirs
soient en
équilibre quoiqu'égaux en pesanteur."
et un peu plus loin "Prévenu de cela, on sçait qu'on ne dérange rien dans l'équilibre des puissances en changeant seulement leur direction en sens contraire: ainsi dans la suposition que tous les couplets sont unis à ne pouvoir se déranger de la figure curviligne qu'ils composent tous ensemble, si l'on fait tourner la chaîne CFD sur la ligne CD comme sur un axe pour prendre la situation opposée, mais toujours verticale CFD, tous les couplets, gardant entr'eux la même situation qu'ils avoient auparavant, tendront au centre de la terre selon les mêmes lignes de direction; & [...] ils se maintiendront toujours en équilibre, & ils ne feront pas plus d'effort pour tomber que s'ils n'étoient point entretenus par quelque cause qui les empêche de se déranger ." |
sous le titre: les remarques suivantes:
On retrouve la courbe caténaire dans les croquis de Christopher Wren pour la construction du dôme de la cathédrale Saint-Paul de Londres ( étude: 1669 ; inauguration : 1708. La solution mathématique interviendra entre les deux dates!). On sait que Wren et Hooke se sont fréquentés et ont échangé des idées; Wren devait être bien informé du principe énoncé par Hooke. Lorsqu'il s'agit d'effectuer une vérification statique de l'équilibre du dôme de Saint-Pierre de Rome (construite en 1626) , Giovanni Poleni utilise lui aussi cette courbe dans ses figures (1748), ainsi que le principe de Hooke.
 |
 |
| Lien vers l'exposition virtuelle Compass and Rule du Musée des Sciences d'Oxford | Croquis de Poleni |
Un Défi Mathématique de la Nature
Quelle est donc la forme que prend une chaîne pendante, et peut-on la calculer?D'autres occasions se présentent de rencontrer cette question lorsqu'on visite les États-Unis, à preuve ces deux exemples ...
 |
 |
| métro à
Chicago (Illinois) N.B: le métro de New York peut convenir aussi! |
Costume de scène
d'Elvis Presley Graceland, Memphis (Tennessee) |
Mais, comme on l'a vu, les Européens y ont été confrontés bien avant. Leibniz, en préliminaire à sa résolution, en souligne l'intérêt (les constructions auxquelles il fait allusion sont celles des courbes, et non celle des bâtiments.)
|
"Le Problème de la Courbe Funiculaire ou Chaînette présente un double
intérêt, premièrement celui
d'étendre l'art d'inventer, autrement dit
l'Analyse, jusqu'à présent incapable d'aborder
convenablement de telles
questions, deuxièmenent celui de faire progresser la
technique des
constructions. Je me suis aperçu en effet que la
fécondité de cette
courbe n'a d'égale que la facilité de
sa.réalisation, ce qui la met en
tête de toutes les Transcendantes. De fait, nous pouvons
l'obtenir et
la tracer à peu de frais, par une construction
de type physique, en
laissant pendre un fil ou mieux une chaînette (de longueur invariable)."
|
Galilée: Erreur ou... Approximation Délibérée?
Fort de son étude des trajectoires balistiques, Galilée, le premier à y réfléchir, évoquait une parabole... Quoi de plus naturel, puisque cette allusion apparait dans son ultime ouvrage Discours sur Deux Sciences Nouvelles (paru en 1638 à Leyde), qui traite de la résistance des matériaux et du mouvement des corps.
"En outre, je dois vous dire une
chose qui à la fois vous réjouira et vous
surprendra, à savoir qu'une
corde plus ou moins tendue a une forme qui approche d'assez près
une parabole...
... la coïncidence est d'autant plus exacte que la parabole est dessinée avec une courbure moindre, ou, pour le dire autrement, qu'elle est plus aplatie; en sorte que si l'élévation de la parabole ne dépasse pas 45°, la chaîne s'ajuste sur la parabole presque à la perfection"
... la coïncidence est d'autant plus exacte que la parabole est dessinée avec une courbure moindre, ou, pour le dire autrement, qu'elle est plus aplatie; en sorte que si l'élévation de la parabole ne dépasse pas 45°, la chaîne s'ajuste sur la parabole presque à la perfection"
Nous avons mis en gras les expressions qui semblent l'innocenter de l'erreur de jugement qu'on lui reproche habituellement, peut-être en raison d'une lecture un peu hâtive de Leibniz. Lequel poursuit son historique du problème en mentionnant celui qui trancha en 1627 la conjecture qu'il prêtait à Galilée: "Joachim Jung, éminent Philosophe et Mathématicien de ce siècle [...] se lança dans les calculs, fit des expériences, et disqualifia la parabole, mais sans lui substituer la véritable courbe."
 |
 |
| Arcs paraboliques de jets
d'eau... devant l'ancienne gare de Saint Louis! Fontaine de Carl Milles, qui collabora avec Eero Saarinen. Elle évoque la rencontre du Missouri et du Mississipi. |
|
L'Histoire a des manières amusantes de se répéter:
* Saarinen avait initialement pensé, lui aussi, à construire une arche parabolique... avant d'opter pour une forme mécaniquement plus naturelle.
* Et, c'est encore plus drôle, des commentateurs mal avisés de son œuvre y virent l'écho des arches du grand pont sur le Mississippi . Or, pas de chance, une arche de pont est le plus souvent parabolique. Un argument heuristique simple est le suivant, dont le principe mécanique est le même, mais dans l'ordre inverse, que celui formulé par Hooke: les cables d'un pont suspendu prennent naturellement la forme, non d'une chaînette (comme le fil qui pend sous son seul poids propre... ) mais d'une parabole, car ils sont soumis au poids du tablier (leur poids propre étant négligeable). Inversons maintenant le soutien, la meilleure répartition des efforts se fera suivant une parabole!
 |
 |
| Eads Bridge, 1874. Saint-Louis (Missouri) | la fausse inspiration: les
arches paraboliques du pont. la vraie, au premier plan: la chaîne pendante! |
À défi, défi et demi: Jakob Bernoulli et Leibniz
La question de la détermination effective de la forme mathématique exacte de la chaîne pendante est adressée par Jakob Bernoulli à Leibniz en Mai 1690. Ce dernier y voit une occasion rêvée de tester l'efficacité du nouvel outil qu' il vient d'introduire, le Calcul Différentiel, qu'ils ne sont guère que quatre à maîtriser à ctte époque: Newton, le grand rival fondateur, les deux frères Bernoulli, Johann et Jakob, et lui-même, qui ne manquera pas de nous signaler sa primauté dans la méthode comme dans l'application (le Mathouriste a mis en gras ces discrets -hum- rappels dans la citation!)|
"Depuis lors beaucoup
s'étaient
attaqués à cette question, mais personne ne
l'avait résolue, jusqu'à ce
que récemment un Mathématicien très
savant me donne l'occasion de la
traiter. En
effet le
célèbre Bernoulli, après avoir dans
différents problèmes employé avec
succès cette Analyse des infinis, s'exprimant par le
calcul différentiel, que j'ai contribué
à
introduire, m'a demandé publiquement dans les
Acta de Mai de
l'année
dernière, p. 218 et suivantes, d'examiner, en en faisant
l'épreuve, si notre calcul pouvait
s'étendre à un problème comme celui de
la
détermination de la Chalnette. Ayant tenté
l'expérience pour lui faire plaisir, non seulement je
parvins au résultat en étant, si je ne m'abuse, le premier à
résoudre ce célèbre
problème, mais je notai de surcroît
les
remarquables applications de la
courbe; voilà pourquoi, à l'exemple entre autres de Blaise Pascal,
j'ai convié les Mathématiciens à le chercher à leur
tour, dans. un délai convenu, pour mettre leurs Méthodes
à l'épreuve."
|
Poursuivant la tradition des défis entre savants,c'est ainsi qu'il lance un petit concours dans les Acta Eruditorum, qu'il anime.
 |
 |
| Le recueil 1691 des Acta, où paraissent les trois solutions. | Statue de G.W. Leibniz à l'Université de Leipzig |
Il n'a pas caché à ses correspondants qu'il détient la solution pour les faire saliver... et cela semble produire l'effet attendu:
|
"Mais pour mieux juger de
l'excellence de votre Algorithme, j'attends avec impatience de voir les
choses que vous aurez trouvées touchant la ligne de la corde ou chaîne
pendante, que Mr Bernouilly (sic!) vous a proposée à trouver, dont je
lui scay bon gré, parce que cette ligne renferme des propriétés
singulières et remarquables. Je l'avois considérée autre fois dans ma
jeunesse, n'ayant que 15 ans, et j'avois démontré au P. Mersenne, que ce n'estoit pas une Parabole."
(Huyghens
à Leibniz, lettre, 9 Octobre 1690)
|
À la fin de l'année 1690, il fait paraître les trois solutions correctes, dûes à Johann Bernoulli, Huyghens et lui même:
|
"Deux seulement firent savoir dans
les délais qu'ils avaient réussi, Christian Huygens, il est inutile
d'insister sur ses grands mérites envers la République des Lettres, et
Bernoulli lui-même, en collaboration avec son jeune frère, dont
l'intelligence n'a d'égale que l'érudition."
|
Voici les
premières pages de chacune des solutions:
 |
 |
 |
| Johann Bernoulli | Leibniz, alias... G.G.L. | Huyghens |
Figure illustrant l'article de Leibniz: construction de la chaînette
Quant à
l'auteur de la question, il a échoué; nous le
savons par Johann:
Mais, direz vous, va-t-on enfin savoir de quelle coube il s'agit? Elle s'exprime, pour le dire avec un vocabulaire actuel, à l'aide de la fonction cosinus hyperbolique, qui est une simple combinaison d'exponentielles:
Très précisément, les courbes solutions du problème de Bernoulli sont les graphes des
|
"Les efforts de mon frère furent sans
succès, pour moi, je fus plus heureux [...]. Il est vrai que cela me
couta des méditations qui me dérobèrent le repos d'une nuit entière."
|
Mais, direz vous, va-t-on enfin savoir de quelle coube il s'agit? Elle s'exprime, pour le dire avec un vocabulaire actuel, à l'aide de la fonction cosinus hyperbolique, qui est une simple combinaison d'exponentielles:
ch (x) = [exp (x) + exp (-x)] / 2
Très précisément, les courbes solutions du problème de Bernoulli sont les graphes des
y = a ch (x/a)
Pas trop fâché contre cette courbe, Jakob Bernoulli y reviendra, assez tardivement (1705). Pour décrire la forme d'une voile , attachée à des baumes horizontales et gonflées par le vent, mais aussi pour... signaler l'équilibre naturel de la voute caténaire! (Meditationes, 1705 in Varia Posthuma, 1744)
Fig 46: la Voute. Fig 51: la Voile!
Deux cercles parallèles, coaxiaux, en fil de fer.. ou de cuivre..
Trempez dans l'eau savonneuse, vous aurez une Caténoïde!
Cédric Villani, Octobre 2011: célébration du Bicentenaire de Galois.
| Pour lire et comprendre le texte
de Leibniz: il est présenté
et analysé sur le site
BibNum
(avec, pour faciliter la tâche, deux versions: latin et
traduction Française);
Mais
attention! On n'y trouvera pas trace de la fonction cosinus hyperbolique:
ce serait un anachronisme. Les fonctions hyperboliques ont
été introduites en 1761 par Lambert,
à l'occasion de sa
preuve de l'irrationalité de Pi. Ce
texte et son analyse sont également
disponibles sur BibNum
.
|
Pas trop fâché contre cette courbe, Jakob Bernoulli y reviendra, assez tardivement (1705). Pour décrire la forme d'une voile , attachée à des baumes horizontales et gonflées par le vent, mais aussi pour... signaler l'équilibre naturel de la voute caténaire! (Meditationes, 1705 in Varia Posthuma, 1744)
Fig 46: la Voute. Fig 51: la Voile!
De Leibniz à Euler
Notre chaînette n'a pas fini de se manifester dans les Mathématiques. Etudiant les surfaces minimales (surfaces minimisant l'aire latérale et s'appuyant sur un contour donné), Euler découvre en 1744 la première surface de ce type, la seule qui soit de révolution: c'est la caténoïde, ainsi dénommée parce que la courbe plane qui l'engendre par rotation n'est autre que la chaînette.Une telle surface est matérialisée par un film de savon, car le goût du moindre effort d'une Nature paresseuse fait que sa position d'équilibre minimise l'aire pour minimiser la tension superficielle. Le Mathouriste a plaisir à renvoyer à l'article correspondant de Wikipédia par un clic sur cette image, dont il se souvient dans quelles circonstances elle fut faite... et dont il tient à saluer très amicalement celle qui l'a réalisée!Deux cercles parallèles, coaxiaux, en fil de fer.. ou de cuivre..
Trempez dans l'eau savonneuse, vous aurez une Caténoïde!
Elégance Mathématique Contemporaine
Dernière apparition recensée: au... gousset de la dernière médaille Fields Française (2010)!
Cédric Villani, Octobre 2011: célébration du Bicentenaire de Galois.
Saarinen
Saarinen voulait
construire une arche
qui s'inscrive dans un carré, aussi haute que large: 630
pieds.
Ce qui ramène à résoudre, avec la
stricte formule
ci-dessus, l'équation
h = 2l = a [ch (l/a) -1]
soit,
en l'inconnue u = l/a
u = l/a ; 2u = ch (u) -1ce
qui était tout
à fait possible, mais aurait fourni une ogive un peu trop
pointue... Cela gênait l'esthétique, et de plus,
il
était prévu qu'au sommet se trouverait un couloir
d'observation panoramique. Pour pouvoir accueillir une
quantité
suffisante de visiteurs (160 environ, sur
une longueur de 20m)
sans que la pente du sol ne présente d'inclinaison trop
dangereuse (et les risques de procès
corrélatifs), il
fallait "aplatir" la chaînette, et c'est ce qui fut fait.
Mathématiquement, on appelle cette transformation une
affinité orthogonale; la formule étant
remplacée
par
y = b ch (x/a)C'est
ce que l'on fait
tous les jours, sans y penser, lorsqu'on représente des
courbes
avec des unités différentes sur les deux axes;
l'aspect
général est conservé.
C'est l'ingénieur Américain d'origine Allemande Hannskarl Bandel (né en 1925 à Dessau, la ville du Bauhaus!) qui donna, à un Saarinen attiré par la chaînette mais insatisfait de sa courbure au sommet, l'idée de l'aplatissement; avec l'équipe d'ingénieurs, il parvinrent à l'équation jugée satisfaisante (en pieds)
Il fut suggéré que c'était toujours une chaînette... mais dont les maillons n'avaient pas tous le même poids, un fil à densité variable, si l'on veut: on parla de chaîne pondérée. Ce n'est pas faux... mais Robert Osserman fait sagement remarquer, dans sa conférence The Geometry of Eero Saarinen's Gateway Arch que l'on peut toujours trouver une pondération convenable qui fait de n'importe quelle courbe convexe préalablement imposée une chaîne pondérée!... à commencer par la parabole, ce qui serait un comble, après avoir insisté sur le fait que l'arche n'en est pas une, et distribué les mauvais points à ceux (très nombreux dans la presse, selon les archives consultées par Osserman) qui s'obstinaient à en voir une dans ce monument.
Le concept de chaîne pondérée ouvre la porte à trop de courbes... dire "une chaînette aplatie" est donc à la fois le plus simple et le plus pertinent.
Un autre apport intéressant fut celui de Carl Milles... oui, celui de la fontaine de la gare de Saint-Louis vue plus haut, et du célèbre Millesgården à Stockholm! Alors que Saarinen avait prévu pour les sections orthogonales de l'arche des carrés, Milles suggéra des triangles équilatéraux, ce qui confère un caractère beaucoup plus élancé au monument. Il resterait encore aux ingénieurs à être... ingénieux dans la conception des ascenseurs, toujours pour s'accomoder des variations de courbure. Ils le furent en effet, créant des trains articulés de "bulles" sphériques.
Une fois la théorie résolue, tout n'alla pas tout seul, mais cela n'a plus grand chose à voir avec les Mathématiques! Le concours architectural s'était déroulé de 1945 à 1947,les fondations ne purent être entreprises qu'en 1959, et l'inauguration eut lieu le 25 Mai 1968: Saarinen ne vit donc pas achever son œuvre la plus emblématique. Avant de devenir un symbole mondialement reconnu de Saint-Louis et de son renouveau, l'arche essuya beaucoup de critiques, dont celle, a priori inattendue... d'être un monument faciste! De fait, un projet similaire avait été conçu par l'architecte Italien Adalberto Libera (1903-1963) pour célébrer, à l'occasion de l'Exposition Universelle prévue pour 1942, les 20 ans de la Marche sur Rome qui avait conduit Mussolini au pouvoir. La Seconde Guerre Mondiale mit un terme à tout cela.
 |
 |
 |
| Salle de
vision panoramique, au sommet. Remarquer la (légère) courbure... |
Localisation des fenêtres au sommet, de part et d'autre (petites taches noires!) | Dernier escalier avant la salle panoramique: vers la descente, la courbure augmente rapidement! |
C'est l'ingénieur Américain d'origine Allemande Hannskarl Bandel (né en 1925 à Dessau, la ville du Bauhaus!) qui donna, à un Saarinen attiré par la chaînette mais insatisfait de sa courbure au sommet, l'idée de l'aplatissement; avec l'équipe d'ingénieurs, il parvinrent à l'équation jugée satisfaisante (en pieds)
y = 68,7672 ch ( x /
99,6682 )
Il fut suggéré que c'était toujours une chaînette... mais dont les maillons n'avaient pas tous le même poids, un fil à densité variable, si l'on veut: on parla de chaîne pondérée. Ce n'est pas faux... mais Robert Osserman fait sagement remarquer, dans sa conférence The Geometry of Eero Saarinen's Gateway Arch que l'on peut toujours trouver une pondération convenable qui fait de n'importe quelle courbe convexe préalablement imposée une chaîne pondérée!... à commencer par la parabole, ce qui serait un comble, après avoir insisté sur le fait que l'arche n'en est pas une, et distribué les mauvais points à ceux (très nombreux dans la presse, selon les archives consultées par Osserman) qui s'obstinaient à en voir une dans ce monument.
Le concept de chaîne pondérée ouvre la porte à trop de courbes... dire "une chaînette aplatie" est donc à la fois le plus simple et le plus pertinent.
Un autre apport intéressant fut celui de Carl Milles... oui, celui de la fontaine de la gare de Saint-Louis vue plus haut, et du célèbre Millesgården à Stockholm! Alors que Saarinen avait prévu pour les sections orthogonales de l'arche des carrés, Milles suggéra des triangles équilatéraux, ce qui confère un caractère beaucoup plus élancé au monument. Il resterait encore aux ingénieurs à être... ingénieux dans la conception des ascenseurs, toujours pour s'accomoder des variations de courbure. Ils le furent en effet, créant des trains articulés de "bulles" sphériques.
 |
 |
| Élément
d'arche: la section est un triangle équilatéral,
qui
rétrécit de la base au sommet. Photo présentée dans le sous-sol du monument. |
Schéma de principe du
train de 8 bulles à 5 places. Document présenté dans le sous-sol du monument. |
Une fois la théorie résolue, tout n'alla pas tout seul, mais cela n'a plus grand chose à voir avec les Mathématiques! Le concours architectural s'était déroulé de 1945 à 1947,les fondations ne purent être entreprises qu'en 1959, et l'inauguration eut lieu le 25 Mai 1968: Saarinen ne vit donc pas achever son œuvre la plus emblématique. Avant de devenir un symbole mondialement reconnu de Saint-Louis et de son renouveau, l'arche essuya beaucoup de critiques, dont celle, a priori inattendue... d'être un monument faciste! De fait, un projet similaire avait été conçu par l'architecte Italien Adalberto Libera (1903-1963) pour célébrer, à l'occasion de l'Exposition Universelle prévue pour 1942, les 20 ans de la Marche sur Rome qui avait conduit Mussolini au pouvoir. La Seconde Guerre Mondiale mit un terme à tout cela.
 |
 |
| Saarinen, ses croquis (noter la
référence aux arcs de triomphe antiques!), ses
maquettes. Photo présentée dans le sous-sol du monument. |
Le projet -jamais réalisé- de Libera pour l'exposition universelle de Rome en 1942. |
Une courbe qui inspire!
En restant encore un peu aux USA...
Route 66 Hall of Fame, Pontiac (Illinois)
Suivant le célèbre conseil de Bobby Troup: "Get
Your Kicks On Route 66"
(allez, laissez vous faire: le plaisir des yeux n'est pas tout, celui
des Maths non plus, tendez l'oreille à Manhattan
Transfer -large choix de versions!-, à moins que
vous ne préfériez Diana
Krall en duo avec Nathalie Cole?), le Mathouriste
a pris la célèbre route, à l'envers de
la chanson, pour s'en fredonner une autre: "Goin' to Chicago"
(un petit
Jimmy Rushing, peut-être? ou un super trio:
John Hendricks, Kurt Elling, Al Jarreau
? ). Et il a eu la surprise de retrouver la
chaînette dans
la cité des vents... à l'intérieur de
son
somptueux musée!
 |
 |
 |
| Comparaison
illustrée:
arche (inversée) et chaîne pendante.
présentée à
l'intérieur du Gateway Arch |
Cette toile fait partie d'une
série, Catenary (1997-2003),
basée sur la chaînette. L'artiste en utilise le
tracé répété sur le
tableau, mais fait
aussi intervenir un fil pendant légèrement en
avant de la
toile, comme le révèle la vue latérale. (Technique mixte)
|
|
Et si vous prenez
l'avion à Washington-Dulles Airport... vous aurez encore le
plaisir de retrouver la chaînette. Pas vraiment un hasard: il
a
été dessiné par Saarinen, en 1958. Frappé par la même malédiction que
celle de
Saint-Louis, il n'en vit pas davantage l'inauguration par J-F Kennedy
en 1962. Son toit est une surface cylindrique
(réalisée
en béton), dont la section droite est une
chaînette,
éventuellement aplatie.
Faut-il l'avouer? Passé dans cet aéroport lors d'un voyage antérieur, le Mathouriste avait pris ces clichés en pensant qu'ils lui fourniraient un exemple intéressant de toit en... cylindre parabolique! Bref, il était lui aussi tombé, au feeling, dans le piège parabolique... Mais, pour sa défense, sans plans cotés précis, n'est-ce pas normal? Ne sommes nous pas dans ce cas qu'évoque Galilée d'un ajustement presque parfait? (Le cas est très différent de celui de l'arche de Saint Louis, car on n'utilise qu'une petite portion de la courbe au voisinage du sommet)
Nous avons des outils mathématiques pour évaluer cette proximité. Le premier, qualitatif, est l'emploi d'un développement limité
L'étudiant un peu plus savant connait la majoration de Taylor-Lagrange, qui garantit que l'erreur est inférieure à ce terme en x4/a4 : cette fois, l'errreur de troncature est contrôlée (s'il sait estimer la constante M, mais cela fait partie de son travail...)
On se retrouve là dans un débat aussi peu évident que celui de savoir si un amphithéâtre Romain est ou n'est pas- elliptique: malgré leur taille imposante, c'est loin d'être indiscutable (voir notre page sur les cylindres).
  |
|
| Aéroport
international Washington-Dulles (Virginia) Le voile en béton qui lui sert de toit a pour section droite une chaînette (aplatie?) |
|
Faut-il l'avouer? Passé dans cet aéroport lors d'un voyage antérieur, le Mathouriste avait pris ces clichés en pensant qu'ils lui fourniraient un exemple intéressant de toit en... cylindre parabolique! Bref, il était lui aussi tombé, au feeling, dans le piège parabolique... Mais, pour sa défense, sans plans cotés précis, n'est-ce pas normal? Ne sommes nous pas dans ce cas qu'évoque Galilée d'un ajustement presque parfait? (Le cas est très différent de celui de l'arche de Saint Louis, car on n'utilise qu'une petite portion de la courbe au voisinage du sommet)
Nous avons des outils mathématiques pour évaluer cette proximité. Le premier, qualitatif, est l'emploi d'un développement limité
y = b ch (x/a) = b [1 + x2/2a2 + x4/4!a4 + o(x4) ]
qui suggère, un peu brutalement, que l'approximation
parabolique
-les deux premiers termes- est correcte "à la puissance
quatrième" de x/a près...
(la brutalité consiste à ignorer les termes
suivants,
sans doute petits, mais non contrôlés avec
exactitude! Et
"cachés" dans le fameux o(x4)...
) L'étudiant un peu plus savant connait la majoration de Taylor-Lagrange, qui garantit que l'erreur est inférieure à ce terme en x4/a4 : cette fois, l'errreur de troncature est contrôlée (s'il sait estimer la constante M, mais cela fait partie de son travail...)
| ch (x/a) - [1 + x2/2a2 ] | < M. x4/a4
Par exemple, si le rapport x/a n'excède
pas 1/5 = .2 (la pente aux extrémités du toit
permet d'estimer au jugé
que ce n'est pas trop déraisonnable), l'écart en
y/b entre chaînette et
parabole est sans doute inférieur au centième!On se retrouve là dans un débat aussi peu évident que celui de savoir si un amphithéâtre Romain est ou n'est pas- elliptique: malgré leur taille imposante, c'est loin d'être indiscutable (voir notre page sur les cylindres).
Et ailleurs? Chaînette ou Parabole?
En Catalogne, Antoni Gaudi a fait un usage explicite de la voute caténaire dans ses édifices, et notamment la Sagrada Familia: c'est sans doute le cas le plus voyant et le plus spectaculaire.Aujourd'hui, certains chercheurs pensent que des voûtes ou dômes qu'ils ont d'abord considérées comme paraboliques seraient, en fait, plutôt du type caténaire... L'argument en faveur de cette thèse serait celui du meilleur équilibre naturel de la structure -l'argument de Hooke, en somme, appliqué intuitivement par les bâtisseurs. Cela concerne, par exemple, les igloos des Esquimaux Canadiens, les huttes traditionnelles en boue séchée des Musgum au Cameroun,
Cela concerne d'abord celle qui, architecturalement, est la mère de toutes les voûtes en arc, la magnifique arche de Ctésiphon (Irak). Bien des ouvrages la mentionnent comme parabolique, mais ne nous y trompons pas: il s'agit dune allusion à la forme générale, pas le résultat d'une étude numérique précise. Au coup d'œil général, en somme... Et puis, il y a toutes celles que des architectes du XXème siècle ont réalisé en béton, grâce aux nouvelles possibilités d'un matériau qui les libérait des contraintes traditionnelles.
 |  |  |
| Ctésiphion |
Freyssinet, hangar à dirigeables à Orly |
Église à Grand Quevilly |
| deux clichés de la collection de Walter Gropius, Bauhaus Museum de Dessau (Allemagne) | ||
Le Mathouriste , qui ne dispose pas d'éléments assez précis pour trancher, vous les présente pour l'instant, avec plus de détails, dans sa page sur les cylindres paraboliques, en compagnie des cylindres elliptiques, sur lesquels des mesures soignées ont établi, justement, la difficulté de reconstituer avec certitude la nature des courbes directrices employées... Peut-être certaines changeront-elles de page, un de ces jours?
Chaînette et Parabole ensemble: why not?
Il est un moment privilégié où les deux courbes peuvent se côtoyer: la construction d'un pont suspendu! Bien sûr, le Mathouriste n'était pas là pour prendre ces clichés (il le regrette, vous vous en doutez bien) de New York en train de devenir New York... Lorsque les câbles sont jetés, ils prennent sous leur propre poids la forme chaînette. Il en va de même des vertigineuses passerelles piétonnes de travail... Mais voici qu'à côté d'elles le tablier se met en place, donnant aux câbles porteurs l'allure parabolique. Quel dommage qu'on n'ait pas laissé subsister la passerelle! Car franchement, aller s'asseoir en amoureux (des mathématiques, plus si affinités) sur un banc pour contempler deux belles courbes et New York qui s'allume, Rhapsody in Blue dans son baladeur ( le pianiste de jazz Marcus Roberts avec Seiji Ozawa, ça vous va? Ou Lang-Lang avec Herbie Hancock? ), ça aurait quand-même de la gueule, n'est-ce pas, M. Woody Allen? (d'accord, vous étiez à Queensboro Bridge... so what? Quant à faire un remake!) |
 |
|
Pont de Williamsburg en
construction (1902) ... oui, celui-là
même qu'arpentera plus tard Sonny Rollins , sax
ténor en bouche...
Source : "The Bridge Builders' Triumph - Williamsburg Bridge Construction" |
Pont de Brooklyn en
construction (1881)
|
Références
Sur la Gateway Arch et Saarinen
- Gateway Arch sur Wikipédia
- Gateway Arch Historic Structure Report
- Eero Saarinen sur Wikipédia
- Eero Saarinen: Shaping the Future Project autour de la vie et de l'œuvre de l'architecte
- Aline and Eero Saarinen papers, 1906-1977 (Archives of American Art)
Mathématiques
- La Chaînette sur le site: Encyclopédie des Formes Remarquables
- Catenary Curve sur Wikipédia
- Le Calcul Différentiel de Leibniz Appliqué à la Chaînette, sur le site BibNum : texte original commenté
- Conférence de Robert OSSERMAN, Professeur Émerite à Stanford University: The Geometry of Eero Saarinen's Gateway Arch (vidéo)
- Article de Robert OSSERMAN (notices de l'A.M.S.), The Mathematics of the Gateway Arch
- D. GRIFFIN, Catenaries, Parabolas and Suspension Bridges
- Acta Eruditoum 1691, sur le site Gallica
- E; HAIRER, G; WANNER, L'Analyse au Fil de l'Histoire (Springer)
- F. GOMES-TEIXERA, Traité des Courbes Spéciales Remarquables, tome 2 (J. Gabay)
- HEMILY (collectif, animé par O.
KELLER) , Textes
fondateurs du calcul
infinitésimal, (Ellipses)
Modèle et Disciple...
Revenir
à la Home
Page du
Mathouriste