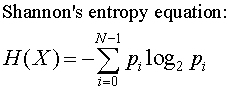|
|

|
|
Le célèbre
schéma...en V.O. |
la
première page de l'article (intégral en lien) |
Ce qui parait, aujourd'hui, une évidentce, frappa
les
esprits à la façon d'un séisme
difficilement
imaginable rétrospectivement. Au point qu'il dut
lui-même
prendre sa plume pour mettre le holà aux abus,
venus,
comme par hasard, des sciences réputées
humaines...
Heureusement, pendant ce temps là, celles qui sont
-forcément, par opposition- inhumaines, allaient faire
fructifier l'héritage de ce papier jusqu'à
permettre aux
spécialistes des premières de
bénéficier de
forfaits téléphoniques illimités pour
échanger en toute sécurité des
Gigabits d'inepties
sur les conséquences de sa théorie.
Mais le Tourisme, dans tout ça?
Le
Mathouriste
le confesse, il aurait bien aimé faire la tournée
des
statues de Shannon érigées aux U.S.A.et visiter
ces lieux
mythiques: le M.I.T., les Bell Labs (voir la couverture de la
publication ci-dessus) où officia Claude Shannon. Ce n'est
pas
encore fait... ce qui ne veut pas dire que l'occasion ne se
présentera pas un jour prochain! Voici d'ailleurs, pour vous
allécher (et, pourquoi pas, si vous passez par
là, faire
un cliché de meilleure qualité et nous en confier
la
publication)

|
|

|
à Gaylord (Michigan),
le 6/10/2000
inauguration en présence de son épouse Betty |
Le scumpteur, Eugene
Daub,
au travail sur son modèle en terre |
au MIT |
Ces vignettes ont été
réalisées à partir des images
originales de la
page
Claude E. Shannon Statue Dedications
que nous vous invitons bien sûr à consulter pour
voir tous
les lieux d'implantation (outre ceux des photos
sélectionnées, Bell Labs, ATT, UCSD) et en savoir
plus!
Et tant que nous en sommes aux emprunts, faute d'avoir été aux
Bell Labs pour assister à l'inauguration de la plaque IEEE...
Par la même occasion, un amphithéâtre était
baptisé au nom de Claude Shannon: une gravure dans le patio le
rappellera désormais à tous les passants.
et dire que le nouveau monde des télécoms y avait
commencé à peu près comme ça, en 1880:
Mais le
Mathouriste
était bien présent, en revanche, parmi les 100
heureux
élus qui assistaient à l'ouverture en France des
célébrations du Centenaire Shannon du 26/10/2016
au
28/10/2016, à l'I.H.P. avec un passionnant
colloque scientifique (ici,
le
programme détaillé)...
Vous êtes jaloux? Vous avez raison, mais vous pourrez les
retrouver intégralement en
vidéo
sur la
chaîne YouTube de l'I.H.P.
, comme si vous y étiez! (et à qui dit-on merci,
croyez
vous, si le streaming sur Internet est possible gâce
à des
flots gigantesques de
1
et de
0
courant sur les fils de cuivre de l'antique
téléphone de
Monsieur... Bell ou sur les ondes de nos engins cellulaires?)
Et comme vous, comme des milliers de visiteurs, il
découvrira
l'exposition que va consacrer le Musée des Arts &
Métiers à
Claude
Shannon, le Magicien des Codes, du
13/12/2016 au 12/03/2017, pour que Shannon ne soit
décidément plus un inconnu.
En attendant, et en complément, il vous propose ici quelques
souvenirs instantanés, et tout particulièrement
le
témoignage d'un grand chercheur ès codes qui a
cotôyé et bien connu Shannon. Le tout
agrémenté de liens choisis et
regroupés dans cette
page pour vous permettre d'en apprendre beaucoup plus sur
cette
passionnante histoire...
Fêter le souvenir de Shannon avec Robert
Gallager
Robert Gallager (professeur
émérite au MIT; s
a
page personnelle)
a donné la conférence de clôture du
colloque... le
bouquet final, en somme! Certes, pour être grand
informaticien,
on n'en est pas moins homme, donc parfois victime de quelques menus
soucis de connexion... mais l'organisation de l'I.H.P. étant
irréprochable, il y a toujours quelqu'un pour
résoudre
ces petites misères... et dans le cas présent, M.
le
Directeur en personne!

|
|
| devant l'affiche de
l'exposition... |
...à remplacer par sa
présentation! On va y arriver... |
Il a notamment tenu à développer le point de vue
de
Shannon sur la manière dont fonctionne un chercheur, ou
plutôt:
doit
fonctionner
pour produire des choses intéressantes (et pas seulement du
papier imprimé...): on sait que cette question a
suscité
de nombreuses réflexions, les meilleures venant de
scientifiques
eux-même: Henri Poincaré, Godfrey Hardy,
Alain
Connes, pour citer les plus remarquables. Que dit Shannon?
Découvrons en images, ses
trois qualités
et ses
six astuces
pour un travail fructueux:

|
|
| 3 qualités de base
pour être un bon chercheur... |
...et 6 astuces
malines pour être créatif! |
Vous trouverez en lien le texte complet de cette conférence:
Creative
Thinking (1952).
Prenons le cas de son premier
trick:
Shannon l'emploie dès le début de son article
fondateur: il
simplifie
en évacuant le
sens
des messages pour attaquer le problème, plus simple, d'une
suite
aléatoire
de symboles.

C'est grâce
à cela qu'il
va parvenir "naturellement" (enfin, presque...) à
définir
une notion-clé de sa théorie, l'entropie,
à partir des probabilités d'apparition
de chaque symbole. Ce nombre forurnira un plancher
à la taille moyenne d'un mot du code qui
garantisse un décodage correct.
L'idée n'était pas nouvelle en soi: elle avait
été empiriquement employée dans le
télégraphe de Morse, par exemple. Le "E",
caractère le plus fréquent en Anglais,
était
codé par le symbole le plus bref, le point. Puis le "T" ,
deuxième caractère par la fréquence
moyenne, par
un trait. Et ainsi de suite; les lettres plus rares étant
représentées par des symboles plus longs (plus
coûteux en bits, dirait-on aujourd'hui), par exemple le "O"
par 3
traits -le fameux SOS devenant ...
--- ... .
Rien ne prouvait qu'on ne pouvait pas faire
mieux; au contraire Shannon réussit à mettre en
évidence une limite indépassable.
Une
deuxième
simplification
est dans l'étude, en première partie, d'un canal
parfait
(chaque symbole est transmis sans erreur); ce n'est que dans la
deuxième partie qu'il aborde un
canal
bruité,
où certains bits sont altérés lors de
la
transmission: cela pose la question de la redondance à
ajouter
à un suite de bits pour détecter et corriger une
erreur,
et conduit à la théorie des
codes
correcteurs. Le tout illustre aussi le
cinquième
trick:
le problème est attaqué d'une façon
structurée et progressive: canal sans bruit/ canal avec
bruit/
pourrait-on faire mieux en tenant compte du sens?
R. Gallager insiste beaucoup sur ce point:
les grandes
idées sont porteuses d'une grande simplicité
(cela n'est nullement contradictoire avec la difficulté d'y
parvenir!). Et prouve l'universalité de son propos en
convocant
des témoins des sciences et des arts... (il aurait pu aussi
bien
citer Newton en physique, et Malevitch en peinture):

|
|

|
| sur le mur de la
maison, rue Lesnická, à Prague, où
résida Albert
Einstein en 1911-1912 |
L'éloge de la
simplicité:
le mathématicien (ou
le physicien, ou l'informaticien!) ne diffère en rien de
l'artiste...
|
Constantion Brancusi (1876-1957):
Princesse X (Bronze poli, 1915-16) |
Le choix des illustrations latérales est celui du
Mathouriste,
et non de R. Gallager, mais on espère qu'il ne
désapprouverait pas.
Les meilleurs codes, ou presque... avec Robert Gallager, et
quelques autres!
(Si vous n'avez jamais
entendu parler de codage, le mieux est de commencer par l'article de
Gabriel Peyré : Claude Shannon
et la compression des donnees sur le site
Image des Mathématique)
C'est ici que nous allons découvrir pourquoi Gallager est
particulièrement qualifié pour parler de Shannon:
il a approché non seulement l'homme, mais
aussi la
limite que Shannon a fixée à
l'efficacité d'un
code!
L'article de 1948 est, en dépit de quelques
réserves
pincées à l'époque de sa sortie, celui
d'un vrai
mathématicien. La preuve, pourrait-on dire en ne se moquant
qu'à moitié, c'est qu'il y
démontre
l'existence de codes "aussi bons que possibles"... s
ans dire
comment en construire! Voici le passsage:
Quiconque a suivi un cours de maths un peu sérieux aura
entendu
ce genre de formulations; quiconque a fréquenté
un
physicien ou un ingénieur les aura entendu rugir
d'exaspération devant un tel énoncé:
"Ah bon! ça nous fait
une belle jambe! et comment fait on, maintenant? "
Si vous n'êtes
pas dans l'une
des catégories socio-professionnelles mentionnées
ci-dessus, vous pouvez néanmoins vous faire une
idée
exacte de l'effet produit avec une situation similaire:
Le
mathématicien: Je sais qu'il y a une fille
(resp. un mec) super-canon qui ne demande qu'à passer la
soirée au lit avec toi...
Vous: Formidable! Et où
puis-je la trouver?
Le
mathématicien: ça, je n'en ai pas la
moindre idée. Mais mes calculs sont formels: je sais qu'elle
existe!
Vous: ...<
CENSURÉ>...
Précisons: Shannon a défini, à l'aide
de
statistiques sur le taux d'erreurs du canal, un nombre qu'il appelle sa
capacité.
Si un message est codé à l'aide de
caractères sur
k
bits, auxquels on a ajouté
n - k bits
redondants (destinés à détecter et
corriger les erreurs), le
taux est le rapport
k / n;
il mesure clairement l'efficacité du codage (plus on ajoute
de
caractères de contrôle, et donc plus on allonge la
représentation d'un caractère, moins on est
efficace
-plus le message coûtera cher en longueur, donc en temps de
transmission).
Ce que dit le théorème, c'est que,
pourvu
que le taux soit inférieur à la
capacité, on peut, pour toute marge d'erreur ε
choisie a priori, si petite soit-elle, trouver un code garantissant un
décodage avec une probabilité d'erreur
inférieure
à ε.
Dans sa conférence, qui
précédait celle de Gallager, Ruediger
Urbank (EPFL) a retracé une brève histoire des
codes correcteurs d'erreur.

|
|
|
Quelques codes "historiques":
auteurs et années d'invention
|
Avant
de déclarer qu'il était
particulièrement heureux
de parler dans une salle réunissant les deux chercheurs qui
ont
le mieux relevé le défi de construction
lancé par
Shannon, auteurs des méthodes les plus récentes,
les plus
efficaces et... les plus appliquées dans les
télécommunications du nouveau
millénaire: Robert
Gallager (
Low
Density
Parity Check codes
, 1963)
et
Claude Berrou (
TurboCodes,
1993) -le
second était le Monsieur Loyal de ces journées.

|
|
|
Ruediger Urbank nous les
présente côte à côte!
Les
flèches de couleur
ont été ajoutées sur ces vignettes
pour vous
aider à les repérer...
|
Voir la
conférence de Ruediger Urbank.

|
|
|
Robert Gallager... et le
principe de ses codes
|
Robert Gallager avait de l'avance (il a publié en 1962)...
TROP
d'avance! Car l'ennui avec les codes, c'est qu'il ne suffit pas de
coder... il faut aussi décoder efficacement! Malheureusement
pour ses LDPC, le décodage demandait beaucoup trop de temps.
Aussi, les TurboCodes se sont imposés
dès les années 1990 pour les
télécommunications, de la NASA aux
réseaux de téléphonie "pour tous" de 3
ème
et 4
ème
génération... Mais les LDPC, forts de
nouveaux procédés de décodage,
reviennent en force pour la 5
ème
génération. Une rivalité technique
qui n'empêche pas, comme on le voit, un contact tout
à fait amical!

|
|
|
De G à D: Urbank ,
Gallager, Berrou
|
Quand Berrou questionne
Gallager... |
Et si vous voulez en savoir plus sur les codes LDPC
Les Débuts d'un Maître
De l'Algèbre des Circuits...
Shannon surprens dès son mémoire de master, en 1937: il y rapproche
algèbre de Boole (
George Boole, 1815-1864) et circuits à relais afin d'améliorer les circuits de communication téléphoniques. Un
article disponible sur la toile; mais dont voici quelques émouvants vestiges d'époque!
|
|
|

|
| Page de garde du tapuscrit |
Puis édité... sous une prstigieuse couverture! |
... à la Cryptographie
Pendant la
Deuxième Guerre
Mondiale, Shannon avait travaillé sur le codage des messages
secrets. Il avait même rédigé en 1945
un rapport
sur le sujet, publié dans une version
déclassifiée
en 1949, sous un titre ... différent! Ya-t-il eu d'autres
modifications... personne ne semble le savoir de nos jours -ou ne veut
l'avouer. Il révèle en tout cas un auteur
très au
courant de l'état de l'art, et perspicace quant à
l'avenir des systèmes cryptographiques.
Anne Canteaut est donc partie de ce texte pour en montrer la pertinence
actuelle à travers les recherches les plus
récentes,
notamment le système
AES
(ou Rijndael), remplaçant
depuis 2001 d'un
DES
vieillissant (1977).
 Video de cette
conférence (aussi en cliquant sur l'image)
Video de cette
conférence (aussi en cliquant sur l'image)Deux "formules de Shannon" ... d'un point de vue
archéologique
Elles figurent dans un autre célèbre (encore!)
article: Communication
in the Presence of Noise (1949)
L'objectif est d'évaluer la capacité
du canal, soit le nombre maximum
de bits par seconde qu'il est possible de transmettre avec une erreur
aussi faible que voulue (autrement dit: le seul maximum raisonnable
pour garantir la quamité de transmission),
présentée dès la première
page de
l'article. Le but est de l'exprimer à partir de la
largeur de bande passante
W du
canal et du rapport
signal sur bruit S/N
( S est
le signal, N le
bruit - N
comme Noise!).
|
 |
La Capacité du Canal
ici, P est mis pour Power
(Puissance du signal)
Cette formule, ce n'est
peut-être pas de la tarte... mais avec Olivier Rioul
(Télécom Paritech), c'est du gâteau!
Son
exposé proposait d'en retrouver (et d'en comparer) les
versions
antérieures. Premier cité:
Ralph Hartley (1888-1970), 20 ans
avant! Son article fondateur est
"Transmission
of Information", Bell System Technical Journal, Volume 7,
Number 3, pp. 535–563, (July 1928).
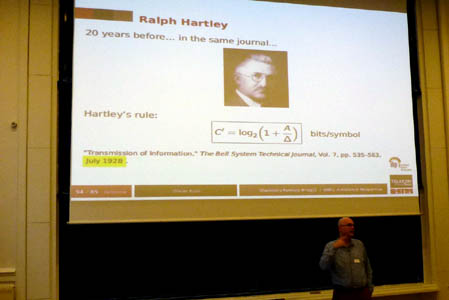
|
|
|
La même
formule?
|
Oui... et non, va-t-il
développer. |
Shannon ne nie d'ailleurs pas y avoir trouvé une source
d'inspiration: il y fait référence dès
la
troisième ligne de son article de 1948. Plus tard, il devait
donner ce commentaire lors d'un entretien évoquant les
grandes
étapes de ses recherches:
"I
started with information
theory, inspired by Hartley’s paper, which was a good paper,
but
it did not take account of things like noise and best encoding and
probabilistic aspects."
Claude Shannon, in
F.W.Ellersick, A
conversation with Claude Shannon. IEEE Commun. Mag. 1984,
22, 123–126.
|
La même chose ou pas? Olivier Rioul et José Carlos
Magossi
ont discuté cette question dans deux articles (2014):
*
Shannon’s
Formula and Hartley’s Rule: A Mathematical Coincidence?
*
On
Shannon’s Formula and Hartley’s Rule: Beyond the
Mathematical Coincidence
On y apprend que, comme toute formule à laquelle
on appose
un nom, la formule de Hartley n'est... pas vraiment de Hartley, mais
qu'il s'agit d'une attribution postérieure, une fois son
article
relu et extrapolé. Et que l'histoire ne s'arrête
pas là: l'année 1948, marquée
de l'article de
Shannon, est aussi celle de la parution de... pas moins de 7 autres
contributions dans le même sens:
dont celle de deux Français, Clavier et Laplume (non, ce
n'est pas un gag...)

|
|
|
Les Frenchies de cette
histoire...
|
Laissez vous raconter tout ça par Olivier Rioul:
sa conférence est en ligne!
Un autre article: L. LUNDHEIM,
On Shannon and
“Shannon’s formulaLe Théorème d'Échantillonnage
(Si vous n'avez jamais
entendu parler d'échantillonnage, le mieux est de commencer
par le premier exposé (Caroline Chaux)
de ce film
des célébrations au CIRM: il est très
pédagogique, avec des exemples sonores très
convaincants)
Ce théorème est aussi présenté sur Wikipedia.
Il est un peu le grand absent de ce colloque, n'apparaissant que
furtivement. Il est pourtant dès la deuxième page
de
Communication
in the Presence of Noise .
Et lui aussi a une histoire qui ne se résume pas
à
"Nyquist-Shannon", pas plus que la formule
précédente n'est réduite à
"Shannon-Hartley". Shannon lui-même cite
Whittaker (1915),
Gabor (1946). Tout en
n'hésitant pas à signaler
que le résultat est à la fois connu de tous en
traitement du signal, prouvé antérieurement dans
un cadre mathématique... sans que l'importance en soit
perçu dans le premier domaine. Mais y aurait--il...
un
problème de communication? Heureusement,
Shannon est là, avec sa perspicacité, pour
rapprocher les deux mondes!

Apparition fugace
chez Olivier Rioul...
|
Tout apparait dans la
deuxième page!
|
Ci-contre:
- l'énoncé
"informel" : doubler la fréquence d'échantillonage
- la formule de reconstruction
- de
nettes références aux auteurs
antérieurs
|
En attendant mieux (une histoire aussi talentueusement
écrite que la précédente), voici, tout
seigneur, tout honneur, l'original, puis quelques
articles analysant ses sources plus ou moins lointaines.. Pour
le plaisir de croiser Lagrange, Cauchy, Borel, De la
Vallée-Poussin... et plein d'autres. Pas si
étonnant, quand on prend la peine d'y
réfléchir:
échantillonner
ou
interpoler,
c'est toujours... travailler, oui, bien sûr! Mais soyons
sérieux: tenter de reconstituer (au mieux possible, en un
sens
à préciser) une fonction
à partir d'un ensemble
discret de valeurs.
|
|
Articles historiques
Commentaires
- H. LÜKE, The Origins of the Sampling Theorem
- A. JERRI, The Shannon Sampling Theorem- Its Various
Extensions and Applications: A Tutorial Review
- R. STANKOVIC, J. ASTOLA, M KARPOVSKY, Some
Historical Remarks on the Sampling Theorem
- R.HIGGINS,
Five Short Stories about the Cardinal Series
- P.L. BUTZER, R.L. STENS, Sampling
Theory for not Necessary Band-Limited functions: A Historical Overview
- P.L. BUTZER & alias, Interpolation
and Sampling: E.T. Whittaker, K. Ogura and Their Followers
(2010)
- M. UNSER, Sampling-50-years-after-Shannon
- M. UNSER, Sampling-60-years-after-Shannon (
transparents d'une conférence à Santorin, 2009)
- E. MEIJERING, A
Chronology of Interpolation: From Ancient Astronomy to Modern Signal and
Image Processing
- E. MEIJERING, A
Chronology of Interpolation... (idem, mais en liste par dates, avec quelques illustrations)
- R J. MARKS II, Introduction
to Shannon Sampling and Interpolation Theory
(livre mis en ligne par l'auteur)
N.B. :
Le poster ci-contre a été
réalisé par Stankovic & alias.
|
Et l'entropie, dans tout ça?
Cette fameuse mesure du caractère aléatoire d'un message
(exprimée à l'aide des probabilités de chacun des N symboles)
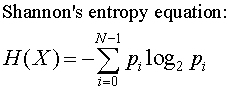
Beaucoup de cours vous la "balancent" abruptement, mais l'auteur, lui, prend soin de montrer qu'elle est nécessaire à partir d'un cahier des charges raisonnable. La démonstration est contenue dans un appendice de l'article.
Et le nom? Court à ce sujet une anecdote, dont la
véracité est discutée: c'est Von Neumann qui le
lui aurait soufflé.
"Vous devriez l'appeler entropie, pour au moins deux raisons:
- la première, c'est que cette fonction a déjà
été utilisée en mécanique statistique, sous
ce nom; donc, elle en a déjà un;
- la deuxième, et c'est la plus importante, c'est que
personne ne sait vraiment ce que cela veut dire, ce qui ne peut que
vous avantager dans les débats." |
Vous trouverez les diverses versions et l'histoire... de cette histoire, dans cette page.
|

|
Et si, malgré l'avertissement, vous voulez vous faire une idée de
l'entropie en théorie de l'information, pourquoi ne pas regarder:
|
Ressources complémentaires sur l'entropie
De difficultés variées, sans doute; mais tous
démarrent élémentairement (avant d'aller plus ou
moins loin), abordent l'incontournable lien avec la physique,
contiennnet un historique de la notion. Il n'est donc pas interdit de
picorer pour constituer son propre puzzle: comme un puzzle,
s'approprier une notion difficile prend du temps, et, croyez en
l'expérience générale de l'auteur de ces lignes,
avec deux textes dont chacun est imparfaitement compris, on peut faire
une assez bonne compréhension générale. N'est-ce
pas normal en la matière, puisqu'on... augmente l'information?
Les deux premiers ont été choisis pour leur taille plus courte...
Toutes les Vidéos du Colloque Shannon-100
Vidéos Complémentaires
Des introductions très
élémentaires