Un Logarithme pour Tsiolkovsky
Constantin
Tsiolkovsky est peu connu en France; et s'il l'est des
physiciens, il est totalement étranger aux mathématiciens. Quant à son équation, elle est célèbre, mais chez les premiers cités.
Mais comme elle emploie le logarithme pour ce qui a longtemps été sa propriété de définition dans les programmes d'enseignement français, depuis 1966, l'homme et sa formule nous ont semblé mériter leur place dans nos pages. En 2019 les nouveaux programmes de lycée ont substitué à cette définition, une autre, certes correcte -encore heureux!- certes "historique" -mais prenant l'histoire à rebours en partant de Cauchy et des équations différentielles (1820). Et qui remplace une définition simple, naturelle, immédiatement accessible, par une autre, intéressante certes, mais bien moins naturelle, plus subtile, donc plus délicate à appréhender par les débutants.
Nous nous proposons, tant qu'à faire anachronique, de la prendre encore plus à rebours, un siècle après Cauchy (1920), pour justifier un retour à l'approche scolaire de 1966 et en défendre la supériorité pédagogique. Car, quoi de plus passionnant que la conquête spatiale? Or, elle a un pionnier, Constantin Tsiolkovsky (1857-1935), et une arme: le logarithme!
Rencontrer le Père de l'Astronautique
Il vous attend, dans le jardin de son isba,
à Kalouga (à 160 km au sud-ouest de Moscou). La partie vitrée en
continu, au premier étage de la maison, est l'atelier-laboratoire de cet homme
étonnant!
Tsiolkovsky, c'est tout à la fois Platon, Thomas More, Jules Verne et Werner von Braun en un seul personnage: philosophe, utopiste, auteur de science-fiction et -last but not least, ingénieur! Tout cela, cependant, autour d'un thème unique: l'espace, et une ambition: le conquérir, le coloniser, pour le bien de l'Humanité. Selon sa célèbre formule (elle figure dans une lettre écrite en ce lieu, en 1911)
Sur son versant littéraire, c'est un auteur de science-fiction qui a lu Jules Verne et l'admire. Ce moyen d'expression est une manière de communiquer sa vision de l'avenir spatial.
Mais bien sûr, ce qui nous intéresse particulièrement ici, c'est l'ingénieur. Découvrons son espace de travail:
Pour passer aux choses sérieuses, c'est à dire aux fusées interplanétaires... il va nous falloir faire un petit détour par les logarithmes, mais rassurez-vous, ça n'a rien de difficile...
Logarithmes pour les Nuls...
La mise en correspondance des termes d'une suite arithmétique et d'une suite géométrique remonte à ... Archimède (L'Arénaire). L'écriture avec des exposants (qu'introduit Descartes dans La Géométrie) des nombres 10, 100, 1000... la met particulièrement en évidence:
ainsi que la propriété, évidente dans ce cas (il suffit de compter les zéros!)
Ces exposants sont ce que l'on appelle les logarithmes (dits décimaux, parce qu'on a utilisé les puissances de 10):
Ainsi, peut-on dire, au début était le logarithme. En témoigne d'ailleurs Fourier, par son enseignement à la tout première promotion de l'École Poytechnique:
Selon la lecture que l'on fait de la formule a p = n (où a reste fixé), si n est donné, p est son logarithme, si p est donné, n est son exponentielle. L'exponentielle est donc le "billet retour" d'un aller fait avec le logarithme; c'est dire combien, dès le début de cette histoire, les deux xont irrémédiablement liés.
On aurait fait tout aussi bien avec des puissances de a=2, comme on le verra ci-dessous explicité par un des pionniers des logarithmes, ou de n'importe quel nombre fixe (dit base des logarithmes)
La publication de l'Écossais Néper est, de fait, la première (1614), et toute la gloire lui revient... Néanmoins, comme cela est fréquent en histoire des sciences, un autre en a fait l'invention indépendalmment à peu près à la même époque, et vraisemblablement une dizaine d'années plus tôt: le Suisse Jöst Bürgi (1552-1632); mais, hélas pour sa notoriété, son ouvrage sur le sujet n'a paru qu'en 1620... Son nom a quand même traversé les époques: il était horloger de précision, et une marque commerciale perpétue son nom! Mais pour ce qui nous intéresse, il était avant tout facteur d'instruments d'optique et assistant de Kepler à Prague, lui fournissant une aide précieuse dans la fabrication des lunettes astronomiques aussi bien que dans les calculs. Mathematiker est en outre la seule activité que mentionne sa pierre tombale.
Le premier à imaginer une correspondance continue entre les deux échelles de grandeurs , et non plus entre deux familles de nombres (espacés en abcisses par le pas de la table) est italien, c'est Evangelista Torricelli (1608-1647), universellement célèbre pour son invention du baromètre. Sa correspondance nous renseigne très précisément:
Ainsi apparaît pour la première fois une courbe logarithmique -qui est plutôt, pour nous, une exponentielle puisque les segments en progression arithmétique sont en abcisses, et les segments en progression géométrique en ordonnées. Elle réapparaît en tant que telle dans le traité de Huygens, Horologium Oscillatorum (1673) et chez Leibniz, comme auxiliaire dans la détermination de la chaînette (ne manquez pas de lire dans nos pages cette autre histoire passionnante), en 1690.
Le Logarithme et l'Aire sous une portion d'Hyperbole
Archimède ayant traité avec succès de la parabole, le problème de l'hyperbole est tout ce qu'il y a de plus naturel; le pionnier s'appelle Grégoire de Saint-Vincent (1584-1647), et son ouvrage, Opus Geometricum Quadraturae Circuli et Sectionum Coni Decem Libris Comprehensum (1647). Mais s'il établit que des aires de "tranches" successives égales correspondent, en abcisses, à des segments en progression géométrique, aucune mention explicite des logarithmes n'apparaît. Il revient à son disciple et ami Alphonse de Sarasa de faire le rapprochement en 1649, deux ans après la mort de Saint-Vincent.
Encore restera-t-il à relier cette aire... au calcul de primitive de la fonction 1/x, ce qui n'est pas si évident! Créditons l'un des pères du Calcul Infintésimal, Leibniz, en 1676 (mais l'autre parent, Isaac Newton, le sait depuis 10 ans au moins; rappelons que leurs méthodes respectives sont farouchement concurrentes). Niklaus Mercator, puis Newton, en tirent parti pour obtenir le développement en série de ln(1+x), source d'un calcul numérique plus commode des logarithmes. N'en disons pas plus à ce stade, car le point est technique; et il serait bien dommage que cette technicité vous détourne de cette histoire, qui ne fait que commencer.
Quand les Monstres Sacrés de l'Analyse renversent les Rôles...
Grand changement avec l'Introduction à l'Analyse Infinitésimale d'Euler (1748): pour la première fois, c'est la fonction exponentielle
qui prend le premier rôle, le logarithme étant défini
comme le billet retour. Voilà au moins la caution d'un "grand ancêtre"
pour le choix de qui apparaît en premier dans un ouvrage
d'enseignement, et qui nous fait voir que le mode d'exposition a varié
au cours de l'histoire, accordant la primeur, tantôt au logarithme,
tantôt à l'exponentielle. S'il y a un reproche à faire au programme de
Terminale S de 2019, ce n'est donc pas dans le choix de la priorité, mais dans la manière de définir l'exponentielle -à savoir par une équation différentielle, et nous y viendrons.
La Fameuse équation...
ou si le Logarithme n'existait pas, il faudrait l'inventer!
Revenons à Tsiolkovsky, et voyons comment le logarithme intervient dans son étude de la propulsion.
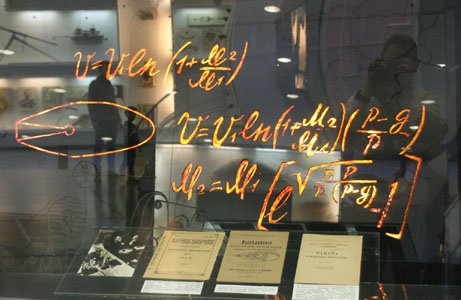
équation de Tsiolkovsky, en fac-similé d'écriture manuscrite.
Sur une vitrine du musée de Kalouga (Russie), présentant des livres du héros.
La conservation de la quantité de mouvement se traduira alors par:
Autrement dit: nous avons besoin d'une primitive pour la fonction 1/x !!! (en reprenant la notation la plus fréquente pour la variable, x plutôt que m).
Rappelons la définition d'une primitive: si la fonction f a pour dérivée la fonction g, f est une primitive de g. On obtient donc un tableau des primitives... en lisant en sens inverse le tableau des dérivées connues. Cela fonctionne très bien pour toutes les puissances entières... sauf une, et c'est celle dont nous avons besoin ici: "Un seul être vous manque, et tout est dépeuplé."
À l'intention de nos lecteurs qui n'ont pas encore goûté aux joies des intégrales, nous pouvons montrer que si elle existe, une telle primitive (définie comme ci-dessus), et que nous noterons l(x), doit avoir des propriétés ... fort similaires à celles des logarithmes que nous avons présentés en introduction.
Ajouter une constante ne change pas la dérivée, donc L(x) = l(x) - l(1) fera aussi bien l'affaire, avec de plus , avec la propriété supplémentaire L(1) = 0.
En dérivant la fonction composée L(ax) , où a est une constante, [L(ax)]' = a. (1/ax) = 1/x = [L(x)]' , et donc les deux fonctions diffèrent d'une constante:
Voilà, il n'y a pas le choix! À partir de là, que le lecteur fasse selon ses connaissances:
Gaz... à tous les étages!
Et, en 1935, il est le premier à proposer le principe d'une fusée à étages, qui sera retenu avec succès, tant par ses compatriotes... que par les Américains.
Voici quelques résultats numériques, en application de l'équation de Tsiolkovsky, concernant -tant qu'à faire!- la fusée Soyouz construite par ses héritiers directs. Les données numériques sont des valeurs moyennes, car il y a eu de nombreuses variantes: il s'agit avant tout, ici, de se faire une idée en ordre de grandeur. Dans le même esprit, on a adopté ve = 3km/s, mais cela dépend des ergols employés. Noter que son premier étage est un peu particulier: il est constitué de 4 boosters indépendants de 45t chacun; d'où la valeur donnée à la masse de l'étage: 4×45t=180t.
Explication des calculs: pour la contribution du premier étage, Δv1 , la masse initiale est la masse totale, la masse finale, la somme de celles des étages 2 et 3, augmentée de la masse à vide de l'étage 1 (masse totale, moins son carvburant, qu'on a épuisé). Puis on largue le premier étage, donc on repart pour Δv2 avec une masse initiale égale à la somme de celles des étages 2 et 3, etc....
On peut faire mieux, avec un peu plus de mathématiques. Ce qui précède est un simple constat: ça ne marchera jamais avec un seul étage (en inversant l'équation, on constate qu'il faudrait que le rapport de la masse de carburant à la masse totale soit de 93%); et trois étages font l'affaire... mais pourquoi pas 2? pourquoi pas 4?
On peut s'en douter: comme souvent en ingéniérie, il s'agit d'un compromis, c'est à dire de la solution d'un problème d'optimisation. Il s'agit de minimiser la masse totale (n'oublions pas que cela veut dire: minimiser le coût, car le carburant coûte cher!), sous la contrainte d'atteindre Δv = 7,9km/s par somme des accroissements dûs à chacun des étages, calculés comme ci-dessus par l'équation de Tsiolkovsky.
La méthode générale a été conçue par Lagrange, mais l'appliquer à ce cas requiert des changements de variables et de fonctions qui la rendent assez longue. Contentons nous donc de résultats donnés pour ve = 2,7 km/s (on reste dans un ordre de grandeur proche): ce sont les relations à l'optimum entre les masses totales Mi des étages, et celle de la charge utile P (satellite):
Il en ressort que le gain est énorme en passant de 2 à 3 étages; il est bien moindre en passant de 3 à 4; et cela va compliquer l'engin, augmenter les risques en cas de difficultés de séparation... 3 étages est donc le bon compromis économie / simplicité. En achevant les calculs dans le cas de étages, on obtient
(source de ces calculs: cours de P. Tsiotras, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta)
Quelques mois avant sa mort, Tsiolkovsky, quoique diminué par l'âge et la maladie qui l'empêchent de venir à Moscou, livre cependant un discours enthousiaste sur l'avenir de la cosmonotique où il évoque sa découverte:
Des logarithmes pour Korolev... aussi!
Celui qui va concrétiser les idées et les calculs de Tsiolkovsky s'appelle Sergueï Pavlovitch Korolev.
Longtemps tenu au secret, il est devenu à son décès un héros national
soviétique -puis russe. Ce miraculé des purges staliniennes (la
mâchoire fracassée par un interrogatoire délicat dans les trop célèbres
locaux de la place Loublianka, envoyé dans le plus dur des camps de
travail à l'extrême nord-est de la Sibérie), il doit son retour en
grâce à l'un des personnages les plus redoutés du régime, Béria.
Celui-ci a décidé en 1939 de récupérer les "intelligences techniques"
envoyées au Goulag et de les remettre au travail dans des...
laboratoires-prisons. Korolev se retrouve dans celui du célèbre
ingénieur aéronautique Tupolev,
qui avait connu les mêmes infortunes et insisté pour le récupérer
auprès de lui. Ce n'est pas encore la liberté, qu'il ne retrouvera
qu'en 1944. Et c'est après la fin de la Grande Guerre Patriotique, comme on dit là-bas, qu'il prendra les rênes du programme spatial de l'URSS.
Rendons-nous dans son bureau, tel qu'il a été pieusement reconstitué -dans ce même fascinant musée de l'usine RKK-Energia:
Évidemment, la plus grande, la plus glorieuse des réussites de Korolev est le vol de Youri Gagarine, le 12 Avril 1961. On s'éloigne un peu des logs et de la règle à calcul, mais comment résister? Surtout que nos images y associent, et ce n'est que justice, le mathématicien le plus impliqué dans cette aventure, comme en témoigne sa présence dans la galerie de portraits de RKK-Energia. Mtsivlav Keldych est un spécialiste de mathématiques appliquées, notamment d'aéronautique et mécanique des fluides, dont les travaux accompagnent tout le programme spatial de l'URSS; il fut en outre Président de l'Académie des Sciences d'URSS de 1961 à 1978.
Il est temps, après cette touchante séquence souvenir, de... revenir à nos logarithmes.
Un programme mal inspiré
Il ne s'agit évidemment pas du programme spatial soviétique, que
nous venons d'évoquer... mais de celui qui, en France, en ce début du
XXIème siècle, impose une défintion de exp d'abord, de Log ensuite, avec trois défauts majeurs:
Et là, c'était de bonne foi. Mais il est facile d'éclaircir ce point essentiel.
Faisons donc, comme disaient les vieux géomètres, l'analyse de la question; lançons la célèbre phrase: Supposons le problème résolu...
Soit donc F une primitive de f sur un intervalle contenant le segment [a,x]. Découpons le en n morceaux, x0 = a, xn = x, e écrivons en faisant apparaître deux fois chaque point intermédiaire, une fois avec le signe -, une fois avec le signe +
À chaque crochet, le théorème des accroissements finis peut s'appliquer, et compte tenu de F'=f (définition d'une primitive)
Les zk sont des nombres dont le théorème des accroissements finis nous assure l'existence, sans autre information que de situer zk dans ]xk-1 - xk [
Mais chaque terme peut s'interpréter comme aire d'un rectangle dont la largeur est, en abcisses, [ xk-1 , xk ] et la hauteur [ 0, f ( zk )] (comptée algébriquement si nécessaire). Donc F (x) - F (a) s'interprète comme une aire, par somme de toutes les aires de ces rectangles. Et plus les largeurs sont étroites, plus cela se rapproche, visuellement, de l'aire sous la courbe. Dans une représentation de l'image sur un écran d'ordinateur, il est impossible de descendre au dessous du niveau du pixel, et ce que nous voyons comme l'aire sous la courbe n'est qu'une somme d'aires de rectangles de largeur 1 pixel... Ce n'est donc pas idiot de compter des petits carreaux, encore fallait-il comprendre pourquoi!
Riemann va, en quelque sorte, "inverser le processus", en partant de zk choisis. Cela peut paraître curieux de prime abord, mais c'est au beau milieu d'un mémoire sur les séries de Fourier (en raison de la forme de leurs coefficients) qu'il lance cette célèbre interrogation:
Mais attention, rien n'est encore prouvé. Ce qui précède se contente de nous suggérer:
Voici, par exemple, les définitions données par l'ouvrage-culte de l'époque, le Condamine et Vissio (1967)
Dans le cahier de cours du Mathouriste, la version "suites" est présentée, dans le cas des donctions monotones, plus simple. Au niveau TC, les seules fonctions que l'on malipule sont monotones par morceaux (avec un nombre fini de morceaux, ce qui permet de découper...). Bien sûr, plus tard, on verra plus compliqué, comme x.sin (1/x)... et bien pire!
Nous reviendrons plus en détail (appendice 3) sur la dérivabilité; admettons la temporairement pour voir comment on enchaîne sur le logarithme... difficile de faire plus simple!
Appendice 3 : Dériver l'Intégrale dans un cas simple, pour ne rien admettre!
Pour convaincre pleinement que la méthode que nous défendons est
la plus élémentaire, encore convient-il de ne rien admettre: le lecteur
mis en position d'accepter le résultat sans preuve pourrait
légitimement se demander si, tout compte fait, nous ne lui demanderions
pas d'admettre un résultat plus délicat que l'existence d'une solution
à l'équation différentielle. À ceux qui se poseraient cette légitime
question, nous proposons ce qui suit... sans obligation pour les
autres. La preuve est plus simple sous une hypothèse plus forte, mais
qui suffit, en pratique, pour toutes les fonctions manipulées en
Terminale.
Mais comme elle emploie le logarithme pour ce qui a longtemps été sa propriété de définition dans les programmes d'enseignement français, depuis 1966, l'homme et sa formule nous ont semblé mériter leur place dans nos pages. En 2019 les nouveaux programmes de lycée ont substitué à cette définition, une autre, certes correcte -encore heureux!- certes "historique" -mais prenant l'histoire à rebours en partant de Cauchy et des équations différentielles (1820). Et qui remplace une définition simple, naturelle, immédiatement accessible, par une autre, intéressante certes, mais bien moins naturelle, plus subtile, donc plus délicate à appréhender par les débutants.
Nous nous proposons, tant qu'à faire anachronique, de la prendre encore plus à rebours, un siècle après Cauchy (1920), pour justifier un retour à l'approche scolaire de 1966 et en défendre la supériorité pédagogique. Car, quoi de plus passionnant que la conquête spatiale? Or, elle a un pionnier, Constantin Tsiolkovsky (1857-1935), et une arme: le logarithme!
Rencontrer le Père de l'Astronautique
Il vous attend, dans le jardin de son isba,
à Kalouga (à 160 km au sud-ouest de Moscou). La partie vitrée en
continu, au premier étage de la maison, est l'atelier-laboratoire de cet homme
étonnant!| statue offerte à la maison-musée par M.I. Lastochkin (1969), réalisée pour obtenir son diplôme de sculpture |
||
Tsiolkovsky, c'est tout à la fois Platon, Thomas More, Jules Verne et Werner von Braun en un seul personnage: philosophe, utopiste, auteur de science-fiction et -last but not least, ingénieur! Tout cela, cependant, autour d'un thème unique: l'espace, et une ambition: le conquérir, le coloniser, pour le bien de l'Humanité. Selon sa célèbre formule (elle figure dans une lettre écrite en ce lieu, en 1911)
|
| Philosophiquement, c'est un disciple de Fiodorov,
personnage très influent de l'époque, fréquenté et apprécié par TolstoÏ
ou Dostoïevski -pour ne citer qu'eux. Il infléchit sa doctrine, le Cosmisme,
aux sources religieuses, ésotériques voire occultistes, vers un aspect
plus scientifique. Pour Tsiolkovsky, la domination de l'homme sur
l'Univers passe par sa conquête, et l'humanité est une , et non plus
divisée: à son époque la Russie est traversée par deux courants
opposés l'un "slavophile", qui a tendance à se refermer sur la
tradition des pays slaves, et l'autre "occidentaliste" qui a le regard
tourné vers l'Europe et l'Amérique... (est-ce si différent aujourd'hui?)
Faut-il voir dans sa volonté de dépasser ces clivages par la conquête
de l'espace une préfiguration de la station MIR ("le monde") et de
l'ISS? |
 |
| Remarque sur le timbre ci-contre: le 12 avril, jour anniversaire du vol de Youri Gagarine (on en reparlera plus bas) est un jour de fête: le jour des cosmonautes! |
Sur son versant littéraire, c'est un auteur de science-fiction qui a lu Jules Verne et l'admire. Ce moyen d'expression est une manière de communiquer sa vision de l'avenir spatial.
Mais bien sûr, ce qui nous intéresse particulièrement ici, c'est l'ingénieur. Découvrons son espace de travail:
| dans son bureau: sa table de travail (et ses lunettes!) |
dans son bureau: le coin dédié aux esxpériences de physique |
l'atelier attenant: il ne dédaignait pas de se mettre à l'établi!
|
Pour passer aux choses sérieuses, c'est à dire aux fusées interplanétaires... il va nous falloir faire un petit détour par les logarithmes, mais rassurez-vous, ça n'a rien de difficile...
Logarithme et exponentielle: la poule et l'œuf?
Ce paragraphe n'a pas l'ambition de faire un historique complet de la saga des logarithmes, aussi passionnante... que longue, mais d'en fournir quelques jalons essentiels, avec le moins de technicité possible, de façon à ne rien perdre de la découverte de Tsiolkovsky.Logarithmes pour les Nuls...
La mise en correspondance des termes d'une suite arithmétique et d'une suite géométrique remonte à ... Archimède (L'Arénaire). L'écriture avec des exposants (qu'introduit Descartes dans La Géométrie) des nombres 10, 100, 1000... la met particulièrement en évidence:| 1 |
10 |
100 |
1000 |
10000 |
100 000 | 1 000 000 | 10 000 000 | 100 000 000 | 1 000 000 000 |
| 100 | 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
ainsi que la propriété, évidente dans ce cas (il suffit de compter les zéros!)
103 × 104 = 107 = 103+4
c'est à dire que la multiplication des nombres proposés se traduit par l'addition des exposants considérés... c'est quand même plus simple, non? Ah, si l'on pouvait faire cela pour n'importe quel produit! Par exemple, 67524 × 485 221 = ??? Pour cela, il faudrait trouver des exposants a et b tels que 67524 = 10a et 485 221 = 10b, et il n'y aurait plus qu'à calculer c = a+b ... et trouver le nombre z=10c.Ces exposants sont ce que l'on appelle les logarithmes (dits décimaux, parce qu'on a utilisé les puissances de 10):
a = log 67524 , b = log 485 221
et, comme ils n'ont rien d'évident (inutile de jouer aux devinettes...), l'enjeu est de construire des tables numériques, dans lesquels on pourra les lire, puis, une fois c = a+b calculé, trouver z en lisant la table en sens inverse. Ainsi, peut-on dire, au début était le logarithme. En témoigne d'ailleurs Fourier, par son enseignement à la tout première promotion de l'École Poytechnique:
Selon la lecture que l'on fait de la formule a p = n (où a reste fixé), si n est donné, p est son logarithme, si p est donné, n est son exponentielle. L'exponentielle est donc le "billet retour" d'un aller fait avec le logarithme; c'est dire combien, dès le début de cette histoire, les deux xont irrémédiablement liés.
On aurait fait tout aussi bien avec des puissances de a=2, comme on le verra ci-dessous explicité par un des pionniers des logarithmes, ou de n'importe quel nombre fixe (dit base des logarithmes)
Des Tables à la fonction, en passant par la courbe
Fourier, qui n'oubliait jamais de faire un bref historique des notions étudiées, l'avait annoncé en introduction à sa leçon:"Nous allons nous occuper dans cette séance de la théorie des logarithmes. Leur découverte, qui fait une des plus intéressantes époque de l'histoire des Mathématiques, est dûe comme on le croit généralement au baron Néper [...]
Leçon du 24 pluviose An IV (13/02/1796)
|
La publication de l'Écossais Néper est, de fait, la première (1614), et toute la gloire lui revient... Néanmoins, comme cela est fréquent en histoire des sciences, un autre en a fait l'invention indépendalmment à peu près à la même époque, et vraisemblablement une dizaine d'années plus tôt: le Suisse Jöst Bürgi (1552-1632); mais, hélas pour sa notoriété, son ouvrage sur le sujet n'a paru qu'en 1620... Son nom a quand même traversé les époques: il était horloger de précision, et une marque commerciale perpétue son nom! Mais pour ce qui nous intéresse, il était avant tout facteur d'instruments d'optique et assistant de Kepler à Prague, lui fournissant une aide précieuse dans la fabrication des lunettes astronomiques aussi bien que dans les calculs. Mathematiker est en outre la seule activité que mentionne sa pierre tombale.
 |
 |
|
| table de logarithmes de Néper: couverture et exemple d'une page (source: Wikipedia) |
Jöst Bûrgi piédestal du monument à Kepler, Weil der Stadt (Allemagne) |
|
correspondance entre progressions arithmétiques et géométrqiues, dans un manuscrit de Bûrgi.
Source: université de Graz, via cette page consacrée à Bürgi. |
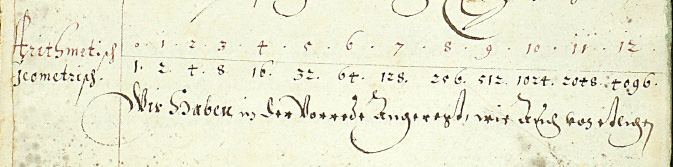 |
|
Le premier à imaginer une correspondance continue entre les deux échelles de grandeurs , et non plus entre deux familles de nombres (espacés en abcisses par le pas de la table) est italien, c'est Evangelista Torricelli (1608-1647), universellement célèbre pour son invention du baromètre. Sa correspondance nous renseigne très précisément:
Ainsi apparaît pour la première fois une courbe logarithmique -qui est plutôt, pour nous, une exponentielle puisque les segments en progression arithmétique sont en abcisses, et les segments en progression géométrique en ordonnées. Elle réapparaît en tant que telle dans le traité de Huygens, Horologium Oscillatorum (1673) et chez Leibniz, comme auxiliaire dans la détermination de la chaînette (ne manquez pas de lire dans nos pages cette autre histoire passionnante), en 1690.
Le Logarithme et l'Aire sous une portion d'Hyperbole
Ce qui servira de fondement au programme de 1966, la détermination
de l'aire sous un arc hyperbolique, n'est pas apparue dans ce qui
précède; mais cela ne veut pas dire que la question n'est pas
simultanément étudiée, bien au contraire. Tout simplement, c'est un
problème qui, le plus naturellement du monde, pourrait sembler sans
rapport avec ce qui précède... en attente d'un petit -ou plutôt d'un
grand- malin qui fera le pont entre les deux.
|
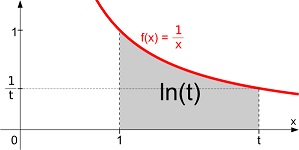 source:: Wikipedia |
Archimède ayant traité avec succès de la parabole, le problème de l'hyperbole est tout ce qu'il y a de plus naturel; le pionnier s'appelle Grégoire de Saint-Vincent (1584-1647), et son ouvrage, Opus Geometricum Quadraturae Circuli et Sectionum Coni Decem Libris Comprehensum (1647). Mais s'il établit que des aires de "tranches" successives égales correspondent, en abcisses, à des segments en progression géométrique, aucune mention explicite des logarithmes n'apparaît. Il revient à son disciple et ami Alphonse de Sarasa de faire le rapprochement en 1649, deux ans après la mort de Saint-Vincent.
Encore restera-t-il à relier cette aire... au calcul de primitive de la fonction 1/x, ce qui n'est pas si évident! Créditons l'un des pères du Calcul Infintésimal, Leibniz, en 1676 (mais l'autre parent, Isaac Newton, le sait depuis 10 ans au moins; rappelons que leurs méthodes respectives sont farouchement concurrentes). Niklaus Mercator, puis Newton, en tirent parti pour obtenir le développement en série de ln(1+x), source d'un calcul numérique plus commode des logarithmes. N'en disons pas plus à ce stade, car le point est technique; et il serait bien dommage que cette technicité vous détourne de cette histoire, qui ne fait que commencer.
Quand les Monstres Sacrés de l'Analyse renversent les Rôles...
Grand changement avec l'Introduction à l'Analyse Infinitésimale d'Euler (1748): pour la première fois, c'est la fonction exponentielle
qui prend le premier rôle, le logarithme étant défini
comme le billet retour. Voilà au moins la caution d'un "grand ancêtre"
pour le choix de qui apparaît en premier dans un ouvrage
d'enseignement, et qui nous fait voir que le mode d'exposition a varié
au cours de l'histoire, accordant la primeur, tantôt au logarithme,
tantôt à l'exponentielle. S'il y a un reproche à faire au programme de
Terminale S de 2019, ce n'est donc pas dans le choix de la priorité, mais dans la manière de définir l'exponentielle -à savoir par une équation différentielle, et nous y viendrons. La Fameuse équation...
ou si le Logarithme n'existait pas, il faudrait l'inventer!
Revenons à Tsiolkovsky, et voyons comment le logarithme intervient dans son étude de la propulsion.équation de Tsiolkovsky, en fac-similé d'écriture manuscrite.
Sur une vitrine du musée de Kalouga (Russie), présentant des livres du héros.
Un avion à réaction, une fusée, avancent par éjection de gaz en combustion (propergols), selon un principe physique analogue à celui du recul du canon, le principe de conservation de la quantité de mouvement du système <fusée> + <propergols> ou respectivement <canon> + <obus>. Cette quantité est représentée par l'expression m.v, produit de la masse par la vitesse. [nous supposons ici que le mouvement se fait sur une droite, pour simplifier; plus généralement v est un vecteur]. Les deux quantités varient en fonction du temps, car le carburant brûlé et éjecté allège la masse de la fusée; on suppose constante la vitesse d'éjection et on la note ve. Suivant le style de raisonnement habituel en physique, pendant un "minuscule" intervalle de temps dt (infinitésimal serait le mot exact) où l'on peut faire comme si la masse était fixe (idéalement, ce n'est vrai qu'à un instant donné), la masse diminuera d'une non moins minuscule variation dm, correspondant à la quantité d'ergols consommés, et la vitesse de l'engin d'une tout aussi minuscule variation dv. |
|
| ci-contre, le livre au centre de la vitrine, et... sa légende en V.O: Édition séparée du troisième article de Tsiolkovsky: "L'Exploration de l'espace cosmique par des engins à réaction" (1914) Le dessin de l'auteur illustre le principe de propulsion; noter la présence d'un humain dans le compartiment avant! (Il sert de filigranne à notre page) |
La conservation de la quantité de mouvement se traduira alors par:
m . dv + ve . dm = 0
Si bien qu'en considérant la vitesse comme une fonction de la masse variable m de la fusée, < fusée> <gaz éjectés> dv / dm = v' (m) = - ve / m
|
Autrement dit: nous avons besoin d'une primitive pour la fonction 1/x !!! (en reprenant la notation la plus fréquente pour la variable, x plutôt que m).
Rappelons la définition d'une primitive: si la fonction f a pour dérivée la fonction g, f est une primitive de g. On obtient donc un tableau des primitives... en lisant en sens inverse le tableau des dérivées connues. Cela fonctionne très bien pour toutes les puissances entières... sauf une, et c'est celle dont nous avons besoin ici: "Un seul être vous manque, et tout est dépeuplé."
À l'intention de nos lecteurs qui n'ont pas encore goûté aux joies des intégrales, nous pouvons montrer que si elle existe, une telle primitive (définie comme ci-dessus), et que nous noterons l(x), doit avoir des propriétés ... fort similaires à celles des logarithmes que nous avons présentés en introduction.
Ajouter une constante ne change pas la dérivée, donc L(x) = l(x) - l(1) fera aussi bien l'affaire, avec de plus , avec la propriété supplémentaire L(1) = 0.
En dérivant la fonction composée L(ax) , où a est une constante, [L(ax)]' = a. (1/ax) = 1/x = [L(x)]' , et donc les deux fonctions diffèrent d'une constante:
L(ax) = L(x) + C
que l'on calcule en faisant x =1 L(a) = L(1) + C = C
soit finalementL(ax) = L(x) + L(a)
et ceci, quelques soient les nombres positifs a et x:La primitive nulle en 1 de 1/x, si elle existe, doit transformer les produits en sommes.
Voilà, il n'y a pas le choix! À partir de là, que le lecteur fasse selon ses connaissances:
- ou il est (un peu) savant, et averti d'une (petite) théorie de l'intégrale, qui garantit l'existence d'une primitive,
- ou bien ... il le deviendra plus tard, et il admet l'existence d'une fonction primitive.
| En attendant, jouons les passe-muraille: oui, le logarithme
existe, et Néper est son prophète. On achève facilement le calcul,
avec, pour la masse et la vitesse des indices "i" pour "initial" et "f"
pour "final": Δv = vf - vi = - ve (ln mf - ln mi) = ve ln ( mi / mf )
Avec vi = 0 -ce qui est le cas au lancement- on obtient le résultat affiché sur la vitre. Tsiolkovsky l'a publiée dès 1903, mais ses manuscrits (exemple ci-contre) attestent qu'il l'avait trouvée dès 1897. Remarque sur l'écriture de Tsiolkovsky: Son écriture fait plutôt apparaître les masses M1 de la fusée "à vide" et M2 du carburant; mi = M1 + M2 et mf = M1 d'où l'écriture équivalente: v = vf - vi = - ve (ln mf - ln mi) = ve ln ( 1 + M2 / M1 )
|
note manuscrite; musée de Kalouga (Russie)
|
 |
 |
| timbre nicaraguéien (1971) |
timbre biélorusse (2002) |
Gaz... à tous les étages!
 |
 | C'est en s'appuyant sur cette équation que, dès 1920, Tsiolkovsky comprend que l'on ne pourra pas satelliser un engin autour de la terre, encore moins aller jusqu'à la lune, avec une fusée "monobloc". Chacun des deux cas demande d'atteindre une vitesse spécifique, la première ou vitesse de satellisation minimale, pour ne pas retomber sur terre (7,9 km/s), la seconde, dite vitesse de libération, pour échapper à l'attraction terrestre (11,2 km/s). |
| Un T-shirt à se procurer au Johnson Space Center... ...from Houston, Texas !!! comme aiment à dire les sax ténors de cet état |
| Désolé, cher Hergé, mais...emmener tout le vaisseau sur la lune, pas question! IM-POS-SI-BLE !!! |
On y va avec ça... |
...Et on abandonne en route toute cette masse inutile après qu'elle ait fait sa part du job! |
 |
 |
 |
| source: www.tintin.com |
LEM National Air and Space Museum, Washington DC (USA) |
Fusée Saturn V Johnson Space Center Houston, Texas (USA) |
Voici quelques résultats numériques, en application de l'équation de Tsiolkovsky, concernant -tant qu'à faire!- la fusée Soyouz construite par ses héritiers directs. Les données numériques sont des valeurs moyennes, car il y a eu de nombreuses variantes: il s'agit avant tout, ici, de se faire une idée en ordre de grandeur. Dans le même esprit, on a adopté ve = 3km/s, mais cela dépend des ergols employés. Noter que son premier étage est un peu particulier: il est constitué de 4 boosters indépendants de 45t chacun; d'où la valeur donnée à la masse de l'étage: 4×45t=180t.
| masse totale |
dont carburant |
Δv = (Tsiolkovsky) |
Δv = (A.N.) |
|
| fusée "monobloc" équivalente |
310 t |
268 t |
3 ln (310 / 42) |
6,00 km/s |
| étage 1 | 180 t | 160 t | 3 ln (310 / 150) | 2,18 km/s |
| étage 2 |
105 t | 95 t | 3 ln(130 / 45) | 3,18 km/s |
| étage 3 |
25 t | 23 t | 3 ln (25 / 2) | 7,58 km/s |
| fusée complète (3 étages) |
310 t | Δv = Δv1 + Δv2 + Δv3 | 12,94 km/s |
Explication des calculs: pour la contribution du premier étage, Δv1 , la masse initiale est la masse totale, la masse finale, la somme de celles des étages 2 et 3, augmentée de la masse à vide de l'étage 1 (masse totale, moins son carvburant, qu'on a épuisé). Puis on largue le premier étage, donc on repart pour Δv2 avec une masse initiale égale à la somme de celles des étages 2 et 3, etc....
| fusée Soyouz à Samara, Russie |
fusée Soyouz à l'exposition VDNKh devant le pavillon du Cosmos (Moscou) |
| [ On voit bien, sur l'image de gauche, 3 des 4 boosters constituant le premier étage ] |
|
On peut faire mieux, avec un peu plus de mathématiques. Ce qui précède est un simple constat: ça ne marchera jamais avec un seul étage (en inversant l'équation, on constate qu'il faudrait que le rapport de la masse de carburant à la masse totale soit de 93%); et trois étages font l'affaire... mais pourquoi pas 2? pourquoi pas 4?
On peut s'en douter: comme souvent en ingéniérie, il s'agit d'un compromis, c'est à dire de la solution d'un problème d'optimisation. Il s'agit de minimiser la masse totale (n'oublions pas que cela veut dire: minimiser le coût, car le carburant coûte cher!), sous la contrainte d'atteindre Δv = 7,9km/s par somme des accroissements dûs à chacun des étages, calculés comme ci-dessus par l'équation de Tsiolkovsky.
La méthode générale a été conçue par Lagrange, mais l'appliquer à ce cas requiert des changements de variables et de fonctions qui la rendent assez longue. Contentons nous donc de résultats donnés pour ve = 2,7 km/s (on reste dans un ordre de grandeur proche): ce sont les relations à l'optimum entre les masses totales Mi des étages, et celle de la charge utile P (satellite):
| avec 2 étages | M1 + M2 = 600,33 P |
| avec 3 étages | M1 + M2 + M3 = 89,42 P |
| avec 4 étages | M1 + M2 + M3 + M4 = 63,48 P |
| avec 5 étages | M1 + M2 + M3 + M4 +M5 = 54,70 P |
Il en ressort que le gain est énorme en passant de 2 à 3 étages; il est bien moindre en passant de 3 à 4; et cela va compliquer l'engin, augmenter les risques en cas de difficultés de séparation... 3 étages est donc le bon compromis économie / simplicité. En achevant les calculs dans le cas de étages, on obtient
M1 = 3,49 P, M2 = 15,67 P, M3 = 70,36 P
(source de ces calculs: cours de P. Tsiotras, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta)
Quelques mois avant sa mort, Tsiolkovsky, quoique diminué par l'âge et la maladie qui l'empêchent de venir à Moscou, livre cependant un discours enthousiaste sur l'avenir de la cosmonotique où il évoque sa découverte:
musée de l'usine RKK Energia (Moscou) |
« Le rêve le plus ancien de l’humanité est en train de se réaliser ».
(discours enregistré par Tsiolkovsky et diffusé sur la Place Rouge le 1er Mai 1935, extrait) "Depuis la calme et modeste ville de Kaluga, je me permets de me tourner avec des salutations chaleureuses et paternelles vers les colonnes des prolétaires et kolkhoziens du 1er mai. Salut à vous ! [...] Des oiseaux de métal volent dans les airs. Et cela n’est
devenu possible avec nous qu’au cours des dernières années, lorsque
notre Parti, notre gouvernement et nos travailleurs, lorsque tous les
travailleurs de notre patrie soviétique, tous, tout le monde, se sont
unis pour réaliser le rêve le plus audacieux de l’humanité, la conquête
de hauteurs célestes. [...]
|
|
| Maintenant, je suis sûr que mon autre rêve, le voyage interplanétaire, que j’ai théoriquement justifié, se réalisera.Pendant
quarante ans, j’ai travaillé sur un moteur à réaction et j’étais sûr
que la marche vers Mars ne commencerait qu’après plusieurs centaines
d’années. Mais le délai change. Je ne peux pas me refuser le désir
de partager les dernières nouvelles, ma joie comme cadeau du premier
mai pour vous. Récemment, j’ai fait une découverte qui pourrait
déjà faire de vous, les participants des célébrations du 1er mai, les
témoins du premier voyage transatmosphérique."
[ le discours complet est à lire sur ce site] |
 relief, musée de Kalouga (Russie)
|
|
Des logarithmes pour Korolev... aussi!
Celui qui va concrétiser les idées et les calculs de Tsiolkovsky s'appelle Sergueï Pavlovitch Korolev.
Longtemps tenu au secret, il est devenu à son décès un héros national
soviétique -puis russe. Ce miraculé des purges staliniennes (la
mâchoire fracassée par un interrogatoire délicat dans les trop célèbres
locaux de la place Loublianka, envoyé dans le plus dur des camps de
travail à l'extrême nord-est de la Sibérie), il doit son retour en
grâce à l'un des personnages les plus redoutés du régime, Béria.
Celui-ci a décidé en 1939 de récupérer les "intelligences techniques"
envoyées au Goulag et de les remettre au travail dans des...
laboratoires-prisons. Korolev se retrouve dans celui du célèbre
ingénieur aéronautique Tupolev,
qui avait connu les mêmes infortunes et insisté pour le récupérer
auprès de lui. Ce n'est pas encore la liberté, qu'il ne retrouvera
qu'en 1944. Et c'est après la fin de la Grande Guerre Patriotique, comme on dit là-bas, qu'il prendra les rênes du programme spatial de l'URSS. |
 |
||
| Grand hall du musée de l'usine RKK Energia (Moscou) à gauche, divers portraits et un buste du patron, au fond, agrandissement géant de sa plus célèbre photo. |
Korolev et son Spoutnik 1 Peinture au musée de l'usine RKK Energia (Moscou) |
Son bébé... suspendu au plafond du musée de Kalouga |
Rendons-nous dans son bureau, tel qu'il a été pieusement reconstitué -dans ce même fascinant musée de l'usine RKK-Energia:
 |
||
| au dessus du bureau, le portrait de Lénine... musée de l'usine RKK Energia (Moscou) |
... mais sur le mur perpendiculaire, celui de Tsiolkovsky! musée de l'usine RKK Energia (Moscou) | Korolev au travail, dessin (crayon) Hall du musée de l'usine RKK Energia (Moscou) |
|
Et posée sur son bureau, au
centre, bien en évidence... sa règle à calcul, sa "baguette magique"
selon ses collaborateurs. Un modèle court (15cm environ), celui qu'à
cette époque on glissait dans la poche avant d'une
veste ou d'une blouse. Ainsi, elle ne vous quittait jamais. Et
accessoirement, ça vous classait son bonhomme.
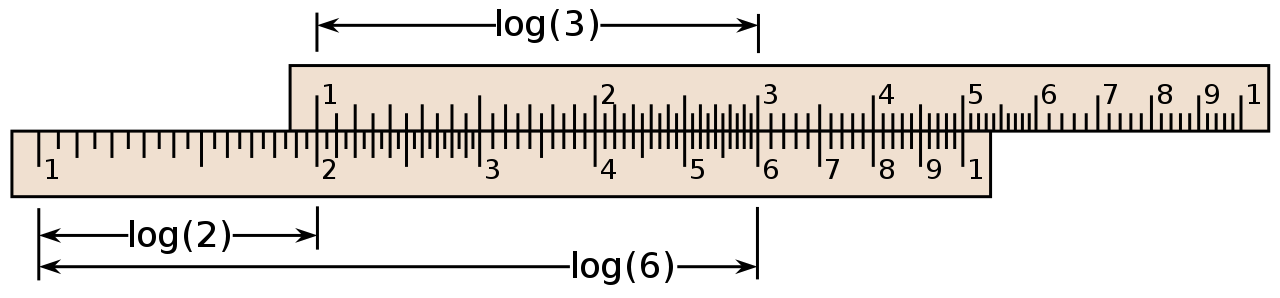
Car le principe d'une règle à calculs, rappelé par le schéma ci-dessus, est d'additionner les logarithmes pour afficher les produits. Et ce, grâce au fait que la graduation est logarithmique.
 |
|
Les
astronautes américains des missions Apollo avaient à bord de leurs
vaisseaux une règle de cette taille, très précisément
une Pickett N600-ES (information donnée par le National Air and Space Museum). Peu encombrante grâce à sa taille (5 pouces), légère (en aluminium!)... what else?
C'est celle qu'a dégaîné "Buzz" Aldrin pour aider son
commandant de bord Neil Armstrong à poser le LEM sur la lune... car
l'ordinateur de bord était tombé en panne au mauvais moment!
C'est aussi le modèle qui a servi à l'équipage d'Apollo 13 lors de l'odyssée de leur retour précipité sur Terre... Une scène du film l'évoque, mais apparamment la règle n'a pas la bonne couleur (n'est-ce pas plutôt celle d'un ingénieur au sol?). Décidément, qu'auraient fait les héros de l'espace sans les logarithmes..., |
 Modèle emporté par Apollo 13; détails dans cette page National Air and Space Museum, Washington DC (USA) |
|
Le Mathouriste et la règle à calcul: un souvenir à la première personne
"Mon père en avait une de la même taille, et le voir s'en servir me fascinait, alors que j'étais encore à l'école primaire. À mes questions, il avait répondu: - ça sert à faire des multiplications et des divisions.  la règle paternelle, en vraie grandeur . C'est un modèle "d'électricien", cela se voit à l'échelle du bas, vouée au calcul du déphasage, cos φ Alors, j'avais décidé de m'en faire une, en découpant des morceaux de carton. Avec un curseur (cadre en carton, et un peu de papier cellophane, sans doute). Ah! C'est que ça avait l'air important, le curseur... Et quand je l'ai essayée, avec ses graduations recopiées sur celles, bien régulières, d'un double-décimètre, ma règle additionnait les nombres, mais refusait de les multiplier. J'en aurais pleuré! Les enfants sont terriblement observateurs, et souvent bien plus, et bien plus rapidement que les adultes. Et bien sûr, j'avais parfaitement remarqué, dès le premier jour, l'inégalité mystérieuse des graduations. Le secret devait résider là-dedans... Mais comment les faire sur mes bouts de carton? J'aurais pu la lui emprunter et recopier, sauf que ça n'expliquerait rien. Et puis, le jour de cette héroïque entreprise, j'étais chez mes grands-parents, où pareil ustensile ne se trouvait pas dans le tiroir de la cuisine. Je voulais trouver le truc tout seul, inconscient de la difficulté; c'est le bon temps où l'on ne doute de rien; d'ailleurs, quoiqu'ignorant le nom de Korolev, j'avais pour autre but de construire une fusée. Aussi balèze que les Russes et les Américains réunis! «Nature qui supporte très mal l'échec», avait un jour conclu les tests psycho-machin-chose qu'on avait tous passés à l'école. Je me demande comment ils avaient trouvé ça à partir de questions d'orthographe, de «Complète logiquement la suite de nombres», et autres «Quelle est la bonne vue de côté de ce tas de briques?», mais je dois reconnaître qu'ils avaient détecté un de mes points faibles... ou fort, peut-être, car ce genre d'humiliation ne peut rester sans vengeance, et ça vous donne envie de continuer la bagarre, hasta la victoria siempre, comme on disait à Cuba. |
||
|
Demander à mon père... oui,
bien sûr. Seulement, il s'était arrêté au Certificat d'Études... De
quoi faire, certes, moins de fautes d'orthographe qu'un bachelier
d'aujourd'hui, mais pas franchement branché sur les logarithmes.
Justement, sa règle lui servait à élever un peu son niveau
professionnel, auxiliaire des exercices d'un cours d'électricité par
correspondance, mêlant théorie et pratique. Ce volet n'était pas moins
passionnant: toutes ces résistances aux bagues multicolres, ces
condensateurs plus ou moins gros, ces lampes -pas encore les
transistors!- connectés en montages différents, ce contrôleur universel
(voltmètre/ampèremètre/ohmètre) assemblé patiemment, la bonne odeur de
l'étain qui fond sur la panne du fer à souder... Bref, il avait appris à l'utiliser, mais ignorant tout des logarithmes, il ne pouvait me dévoiler le pot aux roses.
Il aurait suffi que quelqu'un me dise:« ta
règle additionne? Formidable! Tu as trouvé: la vraie fait la même
chose, rien d'autre, c'est la graduation qui est faite ingénieusement
de telle sorte qu'on lise le produit »... ou quelque chose ccomme ça.
Quelque chose qui m'aurait convaincu que dans mon échec, il y avait une
part de réussite. Je n'avais personne de ce modèle dans mon
entourage, alors, j'ai attendu la Terminale C pour piger enfin. Mais
dès la Première, je faisais les calculs de physique à la règle, parce
qu'à la main, c'était trop chiant, qu'à la règle, c'était plus classe,
et qu'un jour, je serais ingénieur!"
Le Mathouriste , Souvenirs, souvenirs (des sixties)
|
 |
|
 |
P.S. : "L'image ci-contre montre un cours d'électicité de lycée, aux USA, en 1930. Tout le monde calcule à la règle! (une 30cm). Et il y a un modèle géant au tableau, afin d'en montrer l'usage aux élèves. Eh bien, en 1970, dans ma terminale C, nous n'étions que 4 sur 30 à en utiliser une: un groupe de 3 copains -dont j'étais- pour qui aucun ne pouvait être en retard technologique sur les deux autres, et un quatrième... dont le père était prof de maths. Mesurez l'écart! Et pourtant, tout irait très vite ensuite, avec l'apparition; à des pris abordables, de calculatrices scientifiques de poche." |
|
Évidemment, la plus grande, la plus glorieuse des réussites de Korolev est le vol de Youri Gagarine, le 12 Avril 1961. On s'éloigne un peu des logs et de la règle à calcul, mais comment résister? Surtout que nos images y associent, et ce n'est que justice, le mathématicien le plus impliqué dans cette aventure, comme en témoigne sa présence dans la galerie de portraits de RKK-Energia. Mtsivlav Keldych est un spécialiste de mathématiques appliquées, notamment d'aéronautique et mécanique des fluides, dont les travaux accompagnent tout le programme spatial de l'URSS; il fut en outre Président de l'Académie des Sciences d'URSS de 1961 à 1978.
ci-contre:
|

|
|
 Peinture représentant Mtsivlav Keldych (1911-1978) au musée de l'usine RKK Energia |
 |
TITRES:
CITATION (sur le fond noir): "Le nom de S. P. Korolev sera pour toujours associé à l'une des plus grandes conquêe scientifique et technique de tous les temps, l'ouverture d'une éère nouvelle, celle de l'exploration spatiale par l'homme." Le Président de l'Académie des Sciences d'URSS, M.V. Keldych
|
| Panneau présenté au musée de la Cité des Étoiles |
|
" [7h32]
KOROLEV - Youri Alexeïevitch, Je voulais simplement vous rappeler qu'à une minute du top, il faudra encore attendre six minutes environ le début du vol. Pas d'inquiétude, surtout. GAGARINE - Bien compris. Je ne m'en fais pas. [...] [7h34] POPOVITCH, cosmonaute, à côté de KOROLEV - Tu vas comment, Youra? GAGARINE, riant -Comme on me l'a appris! [...] [9h07] KOROLEV - Allumage. GAGARINE - Reçu. Allumage. KOROLEV - Premier étage. Deuxième... Troisième... Lancement exécuté! GAGARINE - ПОeХаЛИ ! (C'est parti!) Niveau de bruit bas dans la cabine. Tout va bien, bon physique, bon moral, pas de problèmes. KOROLEV - Nous vous souhaitons un bon vol.Tout va bien. [...] [9h10] KOROLEV - Expulsion de la coiffe. Tout va bien.. Comment vous sentez vous? GAGARINE - Expulsion de la coiffe... Je vois la Terre... L'accélération s'intensifie, je suis en pleine forme, moral parfait. [9h11] KOROLEV - Beau travail, parfait. Tout se passe très bien. GAGARINE - J'observe les nuages, la base... C'est beau, oh! Une vraie splendeur!" relevé des dialogues, rapporté parYves Gauthier, Gagarine ou le Rêve Russe de l'Espace (Gingko éditeur)
|
|
électrocardiogramme du héros au départ: un bref instant de stress, tout de même!
(Musée des Cosmonautes, Moscou) |
Présentation du Vostok de Gagarine (musée de l'usine RKK Energia)
|
Il est temps, après cette touchante séquence souvenir, de... revenir à nos logarithmes.
Un programme mal inspiré
Il ne s'agit évidemment pas du programme spatial soviétique, que
nous venons d'évoquer... mais de celui qui, en France, en ce début du
XXIème siècle, impose une défintion de exp d'abord, de Log ensuite, avec trois défauts majeurs:- Elle est plus compliquée (que celle qui commence par Log, primitive de 1/x), donc plus difficile à comprendre et assimiler;
- Il faut admettre davantage de choses:
- mais surtout, surtout... elle brouille complètement les niveaux de difficulté entre les équations linéaires du premier et du second ordre, c'est cela que nous ne lui pardonnons pas!
|
Pourquoi il est inopportun de définir exp par y' = y, y(0) = 1
BASE: si on a défini Log comme primitive de 1/x, et exp comme sa fonction réciproque, on peut résoudre par le calcul:(vous pouvez sauter si vous ne voulez pas le savoir, pas de problème! Mais ici, pas de gros calculs, juste quelques exemples pour réfléchir à l'affaire...)
Bref, les équations du
premier ordre (attention, linéaires!) n'offrent aucun mystère. On a
presque envie de dire qu'elles ne sont pas drôles: une fois la
technique assimilée, on s'ennuie un peu....
ET MAINTENANT, REGARDONS QUELQUES CAS DU SECOND ORDRE: Voici quelques équations,
volontairement choisies "ressemblantes" au sens où leurs coefficients
sont simples, et qu'on a juste échangé quelques places, quelques
signes, mis un 2 à la place d'un 1... Juste quelques petites farces pas
méchantes, n'est-ce pas? Voire! Lesquelles savons nous résoudre, et
lesquelles risquent de nous faire sécher?
Quant à (8), pour laquelle on a, en tout et pour tout, changé le coefficient de y', de 1 en 2... elle est à nouveau résoluble élémentairement. Prenez donc une nouvelle fonction inconnue z, en posant y ( x ) = z ( x ) / x (bien sûr, il y a moyen de le deviner, car le père Noël ne passe qu'une fois par an, et il n'a pas toujours des changements de variable ou de fonction plein sa hotte), et si vous ne commettez pas d'erreur de calcul, vous verrez que z est solution d'une inoffensive équation à coefficients constants. Pour nous résumer cette brève introduction aux équations linéaires du second ordre:
Si on aplatit tout, si on perd la vision de ce changement de niveau -et la définition actuelle nous paraît y conduire- on perd beaucoup dans l'apprentissage des mathématiques. Bien entendu, ceci est un avis personnel du Mathouriste, évidemment ouvert au débat si quelque auteur de ce programme, membre de commission, thuriféraire ardent découvre ces lignes et... souhaite défendre ce point de vue. De ceux à qui il a été imposé, il n'a encore rencontré personne qui ait envie de plaider cette cause; et il a essayé, en vain, de savoir qui avait lancé cette idée! Remarque finale :
Un cas extrêment important est celui de la mécanique céleste, avec le fameux problème des trois corps: considérant la Terre, la Lune, et un vaisseau spatial en orbite autour de cette dernière, tout calcul exact de la trajectoire de ce dernier est impossible. Tout est calculable si on considère la lune et le vaisseau, à partir de la loi d'attraction universelle d'Isaac Newton. Mais justement, parce que cette loi est universelle, l'attraction de la Terre ne peut pas être négligée dans un modèle réaliste... or, il faut bien calculer comment ça se passe! La loi est dure, mais c'est la loi.... |
Appendice 1 : Primitive et Intégrale: pourquoi l'une se ramène à l'autre
ln(x) comme intégrale de 1 à x de 1/t, est-ce vraiment plus simple, comme nous l'avons prétendu? Commençons par explorer un peu le lien, pas si apparent, entre "surface sous la courbe" et primitive.En commençant par de l'authentique, du vécu!|
Le Mathouriste, la primitive, et l'aire sous la courbe: un souvenir à la première personne "J'ai toujours été agacé -pour ne pas dire plus- par le manque de coordination des cours de maths et de physique. Cette dernière avait sempiternellement besoin d'une notion pas encore vue en maths... Ah, mais ils osent tout, ces physiciens! Il faut avoir vécu un cours de thermodynamique sans avoir été initié à la délicate question des dérivées partielles pourse faire une idée de la cata... déjà que la thermo, en soi... mais passons, insister serait s'écarter dangereusement. Ce qui m'attriste, c'est qu'un demi-siècle après mes études, non seulement rien n'a changé, mais parfois la situation a empiré, le divorcce s'est accru: les programmes s'ignorent mutuellement , les commissions de réforme des programmes ne se parlent pas, et l'on peut encore entendre l'argument surranné: «pas grave, on fera notre tambouille nous-même...». L'avatar le plus récent, le plus aberrant, est la sortie des séries de Fourier des programmes de Mathématiques Spéciales. Les Américains et les Russes ont sûrement plein de défauts, mais je ne les vois pas faire une chose pareille. So French... Alors, quand j'étais élève, de temps en temps, j'osais, sinon une rébellion, du moins un geste ostentatoire de mauvaise humeur motivée. Un jour, en Terminaale C, un devoir à la maison comportait une question dont la réponse nécessitait le calcul d'une primitve de 1/x. Et votre serviteur écrivit dans sa copie: «La fonction logarithme n'ayant pas encore été étudiée en mathématiques, il nous est impossible de répondre à cette question.» ET TOC !!!! Vous remarquerez la légère mauvaise foi de l'auteur: pour écire ça, il devait nécessairement avoir jeté un petit coup d'œil à son livre de maths, et, tel le champion d'échecs qu'il n'était hélas pas, joué dans sa tête quelques coups à l'avance. Aucun doute, c'était bien pour le plaisir de faire la tronche. Ce que ne manqua pas de voir mon prof' de physique -que j'adorais, au demeurant, ainsi que ma prof de maths, et je tiens à préciser que je leur dois des cours supers grâce auxquels j'ai pris un solide départ en maths sup'. Et ce n'était pas dans un grand lycée parisien, mais dans celui d'une petite préfecture du Bougnathistan, région obscure qui fait une tâche brune, dûe à la légère altitude, au centre (légèrement en bas) de la carte de France, et un trou énorme quand on regarde celle des lignes de TGV. Sans compter la vindicte des présentateurs de la météo, lorsqu'il s'agit de dénoncer la température la plus basse du pays. Le cher prof de physique ne pouvait en rester à ce 1-0 et tenta avec succès l'égalisation: «Soit; mais à ce moment là, vous auriez pu compter les carreaux sous la courbe, pour donner une valeur approximative.» Non, mais, vous imaginez? Compter les carreaux!!! C'est indigne d'un vrai scientifique! Pas question de s'abaisser à cette humiliante trivialité. D'ailleurs, j'ai toujours eu horreur du papier millimétré. Bon, je ne pouvais quand même pas le dire comme ça. Mais j'eus l'inspiration: «Mais enfin, Monsieur, excusez -moi, mais je ne vois pas le rapport entre une surface et une primitive!» Le Mathouriste , Souvenirs, souvenirs (des seventies)
|
Et là, c'était de bonne foi. Mais il est facile d'éclaircir ce point essentiel.
Faisons donc, comme disaient les vieux géomètres, l'analyse de la question; lançons la célèbre phrase: Supposons le problème résolu...
Soit donc F une primitive de f sur un intervalle contenant le segment [a,x]. Découpons le en n morceaux, x0 = a, xn = x, e écrivons en faisant apparaître deux fois chaque point intermédiaire, une fois avec le signe -, une fois avec le signe +
F (x) - F (a) = [ F (xn) - F (xn-1) ] + [ F (xn-1) - F (xn-2) ] + ... + [ F (x1) - F (x0) ]
À chaque crochet, le théorème des accroissements finis peut s'appliquer, et compte tenu de F'=f (définition d'une primitive)
F (x) - F (a) = ( xn - xn-1) f (zn) + (xn-1 - xn-2) f (zn-1) + ... + (x1 - x0) f (z1)
Les zk sont des nombres dont le théorème des accroissements finis nous assure l'existence, sans autre information que de situer zk dans ]xk-1 - xk [
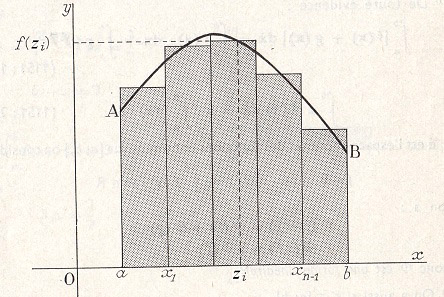
Mais chaque terme peut s'interpréter comme aire d'un rectangle dont la largeur est, en abcisses, [ xk-1 , xk ] et la hauteur [ 0, f ( zk )] (comptée algébriquement si nécessaire). Donc F (x) - F (a) s'interprète comme une aire, par somme de toutes les aires de ces rectangles. Et plus les largeurs sont étroites, plus cela se rapproche, visuellement, de l'aire sous la courbe. Dans une représentation de l'image sur un écran d'ordinateur, il est impossible de descendre au dessous du niveau du pixel, et ce que nous voyons comme l'aire sous la courbe n'est qu'une somme d'aires de rectangles de largeur 1 pixel... Ce n'est donc pas idiot de compter des petits carreaux, encore fallait-il comprendre pourquoi!
Riemann va, en quelque sorte, "inverser le processus", en partant de zk choisis. Cela peut paraître curieux de prime abord, mais c'est au beau milieu d'un mémoire sur les séries de Fourier (en raison de la forme de leurs coefficients) qu'il lance cette célèbre interrogation:
"Et d'abord que doit on entendre par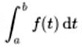 ?" [ "Also zuerst: was hat man unter ?" [ "Also zuerst: was hat man unter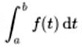 zu verstehen? " ] zu verstehen? " ] |
||
 |
||
| Analyse: les zi sont "donnés" (mais pas explicitement!) par le théorème des accroissements finis. |
La Synthèse de Riemann: les ti sont choisis arbitrairement, et l'on va faire tendre vers 0 le pas de la subdivision. (timbre allemand "non officiel": chacun peut fabriquer ses propres timbres. source: site de philatélie marthématique de Jeff Miller. |
|
Mais attention, rien n'est encore prouvé. Ce qui précède se contente de nous suggérer:
- de faire une théorie de l'aire sous une courbe, à partir de rectangles l'approchant de mieux en mieux, qu'on appelera intégrale de la fonction;
- de démontrer que celle-ci, comme fonction de l'extrémité droite, est dérivable et de dérivée f.
Appendice 2 : Intégrale et Logarithme en Terminale C (Vintage Edition)
On préfère aujourd'hui une vision plus moderne, dont le concept-clé est l'approximation des fonctions. Ainsi, on considère toutes les fonctions en escalier, d'une part inférieures à f, d'autre part supérieures à f, Une fonction est intégrable si l'on peut rapprocher à volonté ( c'est à dire à moins de ε arbitraire donné), les aires d'un escalier supérieur ert d'un escalier inférieur. On peut, par commodité, se ramener à des suites; c'est plus commode à manier, et les suites de fonctions sont aujourd'hui un concept central en Analyse.Voici, par exemple, les définitions données par l'ouvrage-culte de l'époque, le Condamine et Vissio (1967)
 |
 |
| Première étape: l'intégrale des fonctions en escalier (somme des aires des rectangles) | Deuxièrme étape: l'intégrale d'une es fonction générale |
Dans le cahier de cours du Mathouriste, la version "suites" est présentée, dans le cas des donctions monotones, plus simple. Au niveau TC, les seules fonctions que l'on malipule sont monotones par morceaux (avec un nombre fini de morceaux, ce qui permet de découper...). Bien sûr, plus tard, on verra plus compliqué, comme x.sin (1/x)... et bien pire!
 |
 |
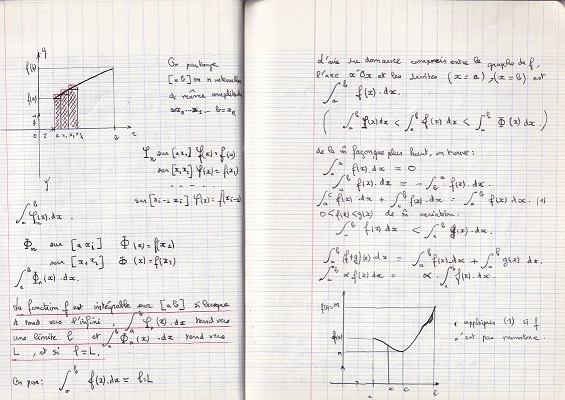 |
| Et à la couverture, les plus perspicaces pourront deviner dans quelle ville cela se passait... |
||
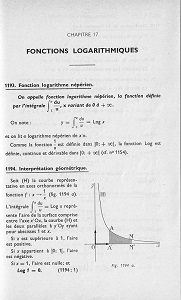
Nous reviendrons plus en détail (appendice 3) sur la dérivabilité; admettons la temporairement pour voir comment on enchaîne sur le logarithme... difficile de faire plus simple!
 |
 |
 |
||
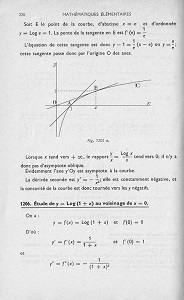
la fonction logarithme dans un autre ouvrage "au goût du jour", celui de C. Bréard, éditions L'École (1964).
Petite pensée nostalgique pour ces beaux ouvrages disparus... Ex fan des sixties,du Bréard de l''École, Que sont devenues toutes tes idoles?
|
 |
 |
||
 |
L'étude de l'exponentielle s'en déduit comme fonction réciproque; on vérifie banalement qu'elle est solution de y’ = y et y(0) = 1, On peut alors intégrer toutes les équations à coefficients constants (Merci à Euler d'y avoir pensé le premier...). Et puis, ces équations, pour simples qu'elle soient, sont d'une utilité universelle, en mécanique comme en électricité... et ça sert à tout le monde, n'est-ce pas, cher Youri? |
| Cours d'électricité, notes manuscrites de l'étudiant Youri Gagarine. Musée de l'usine RKK Energia (Moscou) |
Appendice 3 : Dériver l'Intégrale dans un cas simple, pour ne rien admettre!
Pour convaincre pleinement que la méthode que nous défendons est
la plus élémentaire, encore convient-il de ne rien admettre: le lecteur
mis en position d'accepter le résultat sans preuve pourrait
légitimement se demander si, tout compte fait, nous ne lui demanderions
pas d'admettre un résultat plus délicat que l'existence d'une solution
à l'équation différentielle. À ceux qui se poseraient cette légitime
question, nous proposons ce qui suit... sans obligation pour les
autres. La preuve est plus simple sous une hypothèse plus forte, mais
qui suffit, en pratique, pour toutes les fonctions manipulées en
Terminale.Dérivation de F(x) =
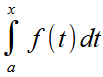 lorsque f est continue et monotone lorsque f est continue et monotoneOn supposera pour ficxer les idées que f est croissante. On fixe x, et on étudie en fonction de h le taux d'accroissement τ (h) = [ F (x+h) - F (x) ] / h 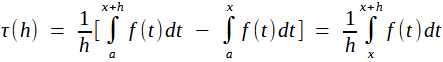
Grâce à la croissance de f : 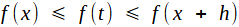 on a on a 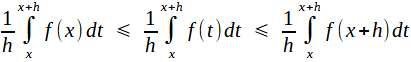 Par rapport à t, f(x) et f(x+h) sont des constantes (n'oublions pas que x est fixé), donc ceci se réécrit
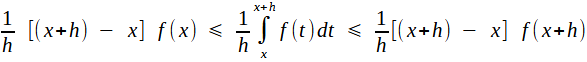 soit finalement 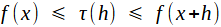 Par continuité de f, f(x+h) tend vers f(x) quand h tend vers 0, et il en va demême pour le taux d'accroissement τ (h) aussi. CQFD! |
Références :
Sur les Logarithmes:
- IREM, E. BARBIN éd., Histoires de Logarithmes (Ellipses)
- IREM, G. MOUSSARD éd., Histoires de Calcul Infinitésimal (Ellipses)
- C. BRÉARD, Analyse, Terminales C et T (L'École 1964)
- M. CONDAMINE, P. VISSIO, Analyse, Terminales C et T (Delagrave 1967)
- M. QUEYSANNE, A. REVUZ, M. GOURION, Analyse, Terminales C,D,E (Nathan 1971)
Sur la Règle à Calcul:
- Musée en ligne des Règles à Calcul du monde entier! (ISRM)
- et comment s'en servir!
- Travaux pratiques possibles sur ce modèle virtuel en ligne: oui, la réglette bouge "à la souris"
- Slide Rules, National Museum of American History
Sur les Équations Différentielles:
- J. HUBBARD, B. WEST, trad V. GAUTHERON, Équations Différentielles et Systèmes Dynamiques (Cassini)
- H. REINHARD, Équations Différentielles, Fondements et Applications (Dunod)
- V. ARNOLD, Équations Différentielles Ordinaires (MIR, Éditions du Globe)
Sur Tsiolkovsky:
- Tsiokovsky sur Wikipedia (plus complet en Anglais, et surtout en Russe ... ne serait-ce que pour les images)
- Œuvres de Tsiolkovsky traduites (essentiellement en Anglais)
- Dossier Tsiolkovsky et la Conquête Spatiale (partie du site: Matérialisme Dialectique)
Sur la Cosmonautique:
Revenir
à la Home
Page du
Mathouriste



