En lisant Ératosthène
Prélude: Dupliquer le Carré... avec Socrate
La Duplication du Carré, autrement dit la construction à la Règle et au Compas d'un carré d'aire double d'un carré donné ABCD, est élémentaire: il suffit de considérer le carré BDEF ayant pour côté la diagonale de l'ancien. En effet, son aire vaut 4 fois la moitié de celle du carré initial, ce qui résout le problème. Si la demande avait été de doubler l'aire d'un autel carré comme celui d'Agrigente (voir page précédente), l'affaire aurait été promptement réglée!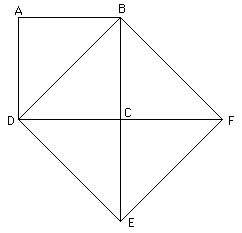
|
|
Cette solution est d'ailleurs exposée dans le Ménon de Platon, dialogue dans lequel Socrate amène un jeune esclave à corriger sa première réponse, qui est de doubler le côté, pour parvenir avec patience et persévérence à la solution correcte. On verra l'erreur du jeune homme se répéter dans l'histoire!
La Duplication du Cube, c'est le même problème... mais dans l'espace (en dimension 3), et non dans le plan (en dimension 2). Simple adaptation? Pas si sûr!
La Lettre d'Ératosthène à Ptolémée III
Nous présentons d'abord la lettre telle quelle, ou plutôt, telle qu'elle est transcrite par Eutocius, un commentateur d' Archimede et d'Apollonius, vivant en Palestine au V-ème siècle de notre ère. Dans ce texte, les liens sur des noms de mathématiciens renvoient à leurs biographies (extérieures à ce site), et les autres à des notes situées plus bas; pour chacune d'entre elles vous trouverez un retour au point où vous avez interrompu votre lecture.
" Eratosthène au roi Ptolémée, salut. On raconte qu'un ancien auteur tragique met en scène Minos faisant préparer une tombe pour Glaukos. Ayant appris que de chaque côté, elle avait cent pieds, il dit : « Tu as désigné certes un petit enclos pour la tombe d'un roi; qu'il soit double; sans détruire ses belles proportions, double donc au plus tôt chaque côté de la tombe ».
Il s'est visiblement trompé : en effet, si l'on double les côtés, la figure plane devient quadruple, le solide, huit fois plus grand. Mais, même chez les géomètres, on recherchait de quelle manière on pourrait doubler le solide donné en lui conservant la même figure. Et ce problème était appelé la duplication du cube; en effet, s'étant donné un cube, ils cherchaient à le doubler. Tandis que tous hésitaient depuis longtemps, Hippocrate de Chios le premier, trouva que, si entre deux droites données, dont la plus grande est double de la plus petite, on parvient à obtenir deux moyennes proportionnelles en proportion continue, la duplication du cube sera obtenue; et ainsi son hésitation se transforma en une autre hésitation non moins grande.
Quelque
temps après, dit-on, certains habitants de Délos, ayant
reçu d'un oracle l'ordre de doubler un des autels,
tombèrent dans la même hésitation. Ils
envoyèrent donc demander aux
géomètres qui
étaient auprès de Platon,
dans l'Académie, de
trouver pour eux la solution. Ceux-ci s'y étant mis avec ardeur
et cherchant à trouver deux moyennes proportionnelles entre deux
droites données, Archytas
de Tarente, dit-on, trouva la solution
au moyen des demi-cylindres, tandis qu'Eudoxe la
trouva au moyen
des lignes dites courbes. Mais à tous il arriva de donner la
démonstration sans qu'ils pussent la réaliser
effectivement et en faire l'application pratique, à l'exception
de Ménechme qui
y réussit un peu, d'une manière
laborieuse. Nous
avons, par contre,
imaginé une méthode instrumentale facile, par
laquelle
nous avons trouvé non seulement deux moyennes
proportionnelles mais autant qu'on veut. Au moyen de cette
invention nous pouvons changer tout solide compris entre les
parallélogrammes en un cube, ou un solide d'une forme dans une
autre, amplifier en conservant la similitude et faire cela aussi aux
autels et aux temples. Et nous pouvons transformer en cubes les
mesures pour les liquides ou les matières,
comme les métrètes et les médimnes, et savoir,
grâce aux côtés des cubes, combien elles mesurent.
Mon invention peut être utile aussi à
ceux qui veulent
augmenter les
dimensions des catapultes et des balistes; car tout doit être
augmenté
proportionnellement, épaisseurs, grandeurs, trous et les cordes
qui y sont
insérées, si le jet doit être augmenté
proportionnellement, ce qui est
impossible sans l'invention des moyennes..."
|
||||
Notes et Commentaires
Époque: Selon la légende, Minos est fils de Zeus et d'Europe. Conséquence du rapt de la seconde par le premier, déguisé en taureau blanc, et qui l'emmène... en Crète.
Enlèvement d'Europe: Relief, VI-ème siècle av. J.C., musée de Syracuse (Sicile)
Ce qui fait du problème de la Duplication du Cube le plus vieux de l'Humanité!
[ Revenir à la lecture de la lettre ]
Famille:
HIPPOLYTE [...] Enfin en le cherchant je suivrai mon devoir,Et je fuirai ces lieux que je n'ose plus voir.
THÉRAMÈNE
HIPPOLYTE RACINE, Phèdre, Acte I, Scène1 |
Quitter Naxos, un soir...
[ Revenir à la lecture de la lettre ]
Mathématiques: Eratosthène relève l'erreur de Minos, qui sera celle de l'élève de Socrate, puis des Déliens (selon d'autres textes). Ensuite, la lettre renferme un anachronisme manifeste (qui peut tout autant émaner d' Eutocius): Platon nait en en 427 avant J.-C., soit l'année même de la peste: difficile de le parer d'un génie si précoce qu'il ait étudié la question à sa naissance! Inversement, la résistance du problème aux efforts des Géomètres explique que son étude soit restée d'actualité dans l'Académie de Platon; il n'est pas impossible que la légende ait valeur de métaphore: qui résoudrait une telle difficulté serait capable de juguler la peste...
[ Revenir à la lecture de la lettre ]Roublardise: Eratosthène termine en soulignant l'intérêt de sa méthode personnelle, en termes d'applicabilité pratique, tant dans le domaine civil (les mesures) que militaire (la construction "des catapultes et des balistes"); il en escompte sans doute quelque avantage, en espèces sonnantes et trébuchantes... Les Mathématiques Pures (nous soulignons toujours, aujourd'hui, le caractère exemplaire des Mathématiques Grecques à cet égard), c'est fort bien, mais sans doute est-il utile, ne serait-ce que pour faire financer ses travaux, de faire ressortir auprès des "politiques" les retombées des applications potentielles! Bref, les Splendeurs et Misères de la Recherche ont aussi une longue histoire, qui n'est pas née d'hier.
[ Revenir à la lecture de la lettre ]
Moyennes Proportionnelles
Elles sont la base de toutes les méthodes de résolution. Les rapports de longueur constituent un outil privilégié des Mathématiques Grecques, et tout problème se doit d'être reformulé en de tels termes si l'on veut espérer le résoudre.La duplication du cube, autrement dit la recherche du côté x d'un cube de volume double du cube de côté a, peut s'écrire comme la recherche de deux nombres x et y que l'on va intercaler entre a et 2a, d'où l'appellation:
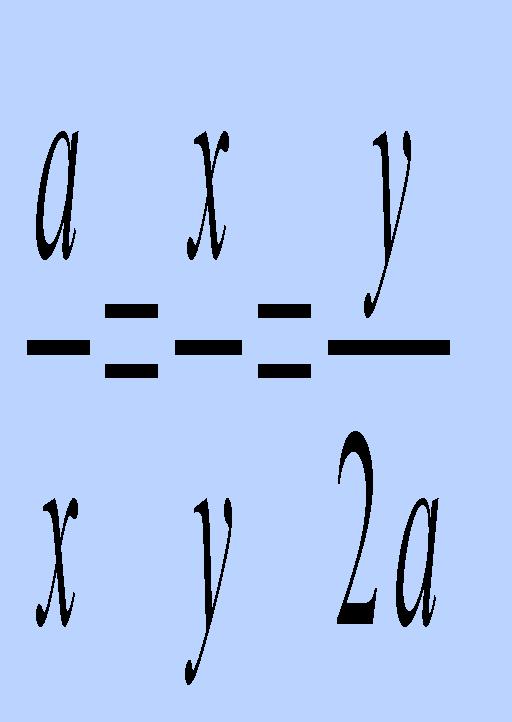
[ Revenir à la lecture de la lettre ]
Plus généralement, on peut rechercher l'intercalation de moyennes entre a et b (au lieu de 2a),
Et comme le souligne l'auteur lui-même, on peut pousser plus loin la généralisation à trois moyennes x , y , z , ou plus ("non seulement deux moyennes proportionnelles mais autant qu'on veut").
Les deux pages suivantes montreront comment ce principe est utilisé dans la construction de machines ou l'emploi de courbes autres que la droite et le cercle: c'est la première fois que les Mathématiques vont aller Au Delà du Compas, expression que nous empruntons au titre de l'exposition Oltre Il Compasso du très beau Musée des Mathématiques (situé à Florence):
Faites lui une visite virtuelle, vous ne devriez pas le regretter!
