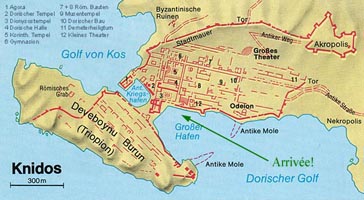
Le site de Cnide
Arriver à Cnide...
Si l'on peut se permettre un conseil... arrivez par la mer! C'est facile, car la croisière en goélette est une activité florissante sur la côte sud du pays; ainsi vous découvrirez le site dans toute sa majesté. Et vous partagerez la sensation qu'Eudoxe, parti étudier auprès d'Archytas de Tarente, éprouva lui-même à son retour d'Italie...
Heureux qui, comme Eudoxe...
(Arrivée sous le petit théâtre -4500
places quand même!)
Privilège
et fortune du site, il possédait deux ports: le port de
commerce, aujourd'hui... de tourisme, et le port militaire, de l'autre
côté de l'ishtme. Rien n'a changé
à la disposition des lieux depuis l'Antiquité...
 |
 |
| port militaire (des trirèmes) | port de commerce |
 |
 |
...Monter à la tholos d'Aphrodite...
La Belle n'est plus
là, vous le savez déjà: elle a disparu
lors d'un incendie; on ne la connait que par des copies Romaines. Mais
monter offre des vues splendides, et n'est-ce pas poursuivre notre
retour "dans les sandales du Mathématicien" ? C'est sans
doute par ce large escalier qu'il remonta vers la ville!
Le socle de la tholos d'Aphrodite : on devine la forme circulaire, en l'absence de recul...
Derrière, le port militaire.
C'est donc ici que les Cnidiens -et pas qu'eux!- venaient admirer le chef-d'œuvre de Praxitèle (voir le site de l'exposition 2007 au Louvre). Car selon Pline l'Ancien, "beaucoup ont fait le voyage à Cnide pour la voir"... La forme circulaire du temple était, merveille de la Géométrie, d'une fonctionnalité parfaite à cet égard: on pouvait faire le tour de la statue et l'observer sous toutes ses ... faces. Les gens de Cnide avaient eu l'excellente idée de prendre celui des deux modèles proposés par l'artiste, que n'avaient pas retenu les citoyens de l'île voisine de Kos, à l'origine de la commande.
Aphrodite de Cnide, copie (Musée du Capitole, Rome) sur un bel octogone de marbre
... et redescendre vers le théâtre, à la rencontre du cadran!
Ne nous laissons pas trop distraire... et revenons à notre cadran, que nous apercevrons assez vite en nous dirigeant vers le petit théâtre. Il devait se situer à l'intersection de deux artères importantes, tout en respectant un orientation plein sud: tant qu'à faire d'être pratique!
Le cadran, tel qu'il apparait pour la première fois au promeneur... en fait, de dos!
( On domine, sur la gauche, le port de commerce )
... et son indispensable complice, sans lequel il ne peut fonctionner!
Le cadran
L'observation de sa cavité laisse apparaître des lignes gravées, cercles et droites:
Il s'agit d'un type de
cadran relativement courant dans le monde Hellénistique
(puis Romain, par simple imitation), le cadran
conique d'axe polaire : c'est un cône de révolution, d'axe paralléle à l'axe de rotation de la terre); le
principe reste celui d'un cadran équatorial..
Schéma du cadran; voir ici plus de détails de principe (page faisant partie de ce site).
Le style (perdu!)
était horizontal, son extrémité sur
l'axe du cône. Autrement ditl il ne s'agit pas d'un style
polaire: ce n'est pas l'axe du cône, mais il suffit d'y
placer un point, O sur le schéma.
Reconstitution empirique: du style au ... stylo!
Le temps a manqué pour effectuer un positionnement exact de l'extrémité...
Vérification expérimentale du type du cadran: le cône des lignes horaires (le sommet S est au dessus du plan horizontal!)
Reconstitution empirique: du style au ... stylo!
Le temps a manqué pour effectuer un positionnement exact de l'extrémité...
Une
caractéristique de ce type de cadran est d'avoir des lignes
horaires régulièrement espacées, qui
sont des
génératrices du cône. Nous avons
essayé de
le vérifier sur les images, en prolongeant les
génératrices au delà du sommet du
cône. Ce
n'est certes pas un travail de précision... mais cette
petite
expérience montre assez bien ce qu'on attendait par la
théorie!
Vérification expérimentale du type du cadran: le cône des lignes horaires (le sommet S est au dessus du plan horizontal!)
Pour ceux qui
voudraient voir l'évolution du tracé droite
après droite, ou presque: étape
3, étape
4, étape
5, étape
6.
Si -car ce n'est pas obligatoire!- le demi-angle au sommet du cône est égal à la latitude du lieu, soit aussi bien à l'angle entre l'horizontale et l'axe du cône, une génératrice et une seule sera horizontale... et la section du cône par un plan horizontal, c'est à dire sa table supérieure, parabolique!
Il semble bien que ce soit le cas pour le cadran d'Eudoxe... ou alors, on n'en est pas loin! (Un brave touriste prend avec lui plein de matériel photographique... mais rien pour mesurer les angles, c'est sûrement un tort!)
Dans le plan horizontal, la parabole (?) ou ellipse très allongée...
L'image met aussi en évidence la génération réglée et la verticalité de la ligne de midi.
Si -car ce n'est pas obligatoire!- le demi-angle au sommet du cône est égal à la latitude du lieu, soit aussi bien à l'angle entre l'horizontale et l'axe du cône, une génératrice et une seule sera horizontale... et la section du cône par un plan horizontal, c'est à dire sa table supérieure, parabolique!
Il semble bien que ce soit le cas pour le cadran d'Eudoxe... ou alors, on n'en est pas loin! (Un brave touriste prend avec lui plein de matériel photographique... mais rien pour mesurer les angles, c'est sûrement un tort!)
Dans le plan horizontal, la parabole (?) ou ellipse très allongée...
L'image met aussi en évidence la génération réglée et la verticalité de la ligne de midi.
Tout ceci
étant dit, il reste, au fond, la question historique
essentielle: ce
cadran est-il d'Eudoxe, comme on nous le dit?
Les ruines sont considérées comme datant de l'époque Hellénistique, période s'étalant du IV-ième siècle au I-er siècle avant J.-C., ou, si l'on préfère, entre la mort d'Alexandre le Grand et la conquête Romaine. Eudoxe meurt en 355, et Alexandre nait en... 356; c'est déjà un peu juste!
En fait, ce type de cadran semble courant à cette époque; et on le retrouve en de nombreux endroits du monde méditérannéen: voir cet article; peut-on au moins attribuer la paternité du modèle à Eudoxe? Une consultation rapide ne nous a fourni aucune certitude, ni dans un sens, ni dans l'autre. On ne prête qu'aux riches: il est sans doute tentant pour la ville natale de l'astronome de revendiquer sa griffe... Le Mathouriste se promet d'enquêter de façon plus approfondie dans les bibliothèques; mais si d'ici-là quelque expert en gnomonique visite cette page et peut apporter des précisions, elles seront reçues avec le plus grand plaisir.
Les ruines sont considérées comme datant de l'époque Hellénistique, période s'étalant du IV-ième siècle au I-er siècle avant J.-C., ou, si l'on préfère, entre la mort d'Alexandre le Grand et la conquête Romaine. Eudoxe meurt en 355, et Alexandre nait en... 356; c'est déjà un peu juste!
En fait, ce type de cadran semble courant à cette époque; et on le retrouve en de nombreux endroits du monde méditérannéen: voir cet article; peut-on au moins attribuer la paternité du modèle à Eudoxe? Une consultation rapide ne nous a fourni aucune certitude, ni dans un sens, ni dans l'autre. On ne prête qu'aux riches: il est sans doute tentant pour la ville natale de l'astronome de revendiquer sa griffe... Le Mathouriste se promet d'enquêter de façon plus approfondie dans les bibliothèques; mais si d'ici-là quelque expert en gnomonique visite cette page et peut apporter des précisions, elles seront reçues avec le plus grand plaisir.
L'œuvre d'Eudoxe
Mathématicien, astronome, géographe, Eudoxe laisse une œuvre importante, mais qu'on ne connait qu'à travers ses successeurs, notamment Euclide. Pour nous limiter à l'essentiel de ses contributions mathématiques, nous citerons sans commentaire, mais avec des liens (presque tous externes) choisis:- la Méthode d'Exhaustion pour le calcul des aires et des volumes, très employée par Archimède;
- la Kampile, courbe du quatrième degré utilisée pour résoudre le problème de Délos (notre page générale, la page de la solution d'Eudoxe, une autre page relative à cette solution);
- l'Hippopède, courbe de l'espace résultant des mouvements relatifs des sphères concentriques constituant son système planétaire. Sur cette page (partie de ce site), vous visualiserez la théorie astronomique d'Eudoxe; vous pouvez aussi voir ici une machine de simulation. L'ouvrage de R. D'HOLLANDER ci-dessous contient aussi de copieuses informations.
Références
- R. D'HOLLANDER, Sciences Géographiques dans l'Antiquité (IGN)
- G. LLOYD, Une Histoire de la Science Grecque (Points Sciences)
