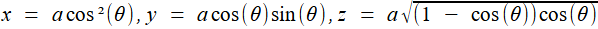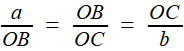Solutions par des Courbes, #1 :
celles qu'évoque Ératosthène dans sa lettre
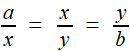
Archytas, par l'Espace!
|
Ératosthène, lettre à Ptolémée III (citée par Eutocius)
|
|
La première solution purement géométrique est, d'une certaine manière... la plus compliquée. Et, deuxième sujet d'étonnement, elle résout par la géométrie dans l'espace un problème plan, ce qui est plutôt insolite, et à coup sûr exceptionnel dans le monde grec. Du coup, la réalisation d'un système de moyennes proportionnelles va passer par la joyeuse rencontre de trois surfaces dans l'espace! Son auteur, Archytas de Tarente (4o8-355 av. J. C) était un philosophe et mathématicien pythagoricien, ami de Platon. |
 Buste d'Archytas de Tarente (Musée de Naples) |
| Article 1: vous avez le droit de sauter ce paragraphe s'il vous paraît trop difficile à suivre... et d'y revenir plus tard; Article 2: si
|
Etape 1 : un p'tit lemme dans un triangle... ou deux!
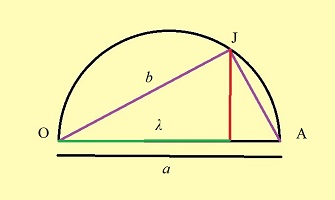
On vous le redonne ici pour le cas où vous arriveriez à cette page... sans passer par la précédente, qui contient à son sujet plus d'informations, notamment sur l'usage musical -ce n'est surprenant quen apprence!- qu'en fait Mersenne.Elle est là, l'ingénieuse idée d'Archytas: utiliser la même figure très simple, mais en la situant dans deux plans distincts; ça n'a l'air de rien, mais si on vous pose une question que vous pensez relever de la géométrie dans un plan, penserez vous à introduire la troisième dimension?
L'étape suivante va être de mettre un peu de dynamique dans tout cela.
Etape 2 : la courbe d'Archytas
Cette courbe que décrit B, c'est la courbe d'Archytas, et nous venons de prouver son existence sans la moindre équation -qui, du reste, aurait été anachronique. Vous pourrez admirer le mouvement du plan auxiliaire et la description associée de la courbe sur cette page du site mathcurve.com de Robert Ferréol. Toujours sans équation, nous pouvons la décrire comme une intersection de surfaces; en effet:
- BC est portée par une verticale dont le pied décrit le cercle de base horizontal; cette verticale balaye un cylindre (de révolution) - le tuyau de plomberie!
- le demi-cercle vertical engendre, par sa rotation, un tore à collier nul.
| Boudin torique, temple d'Apollon à Didymes (Turquie) |
Bijou punique, Musée du Bardo (Tunis) |
La seule particularité de notre cas, c'est le fait que le "trou" n'existe plus (une bague qui ne permettrait le passage que d'un doigt d'épaisseur nulle!), là encore, sans en avoir écrit l'équation; c'est un solide de révolution tout à fait naturel. [voir aussi notre page sur ce sujet]
La courbe d'Archytas est donc une (partie d') intersection entre un cylindre de révolution et un tore à collier nul, dont les axes de révolution sont parallèles. Ce qui n'est pas immédiat à se représenter ou à dessiner... mais les ordinateurs, bien dirigés, peuvent s'avérer là d'une efficacité redoutable à condition de les nourrir d'équations!
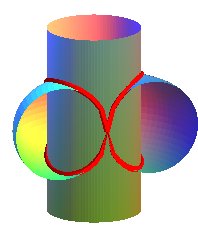 |
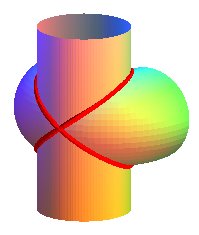 |
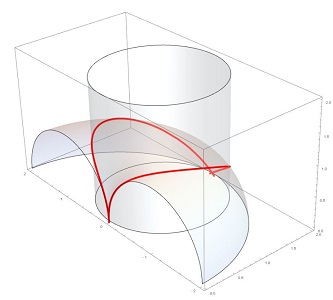 |
| Deux vues opposées site des courbes mathématiques (R. Ferréol) |
Vue "aérienne" globale source: la remarquable page Archytas du wikipedia allemand |
|
Reste à savoir comment elle va contribuer à la duplication du cube... ce sera l'objet de notre dernière étape.
Etape 3 : une "solution"... en théorie!
Notre but est de construire deux longueurs x et y vérifiant, pour a et b donnés,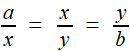 Nous supposerons dans la suite que b < a ; par exemple a=2, b=½ dans le cas de la duplication du cube. |
||
 |
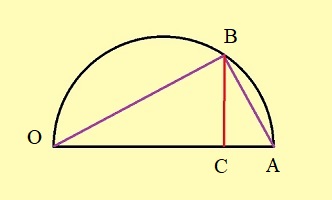
Reprenons les formules (1) et (2) de la première étape, c'est à dire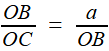 (1) et (1) et 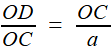 (2) (2)(1) est plutôt bien partie pour avoir l'allure du but visé! x = OB et y = OC seraient alors de bons candidats, à condition de "bien terminer" la deuxième égalité. Or, on a remarqué que le plan (BCD) -orange ci-contre- étant perpendiculaire à OA, le triangle OBD -mauve- est lui aussi rectangle, et donc, considérant l'angle ω = DOB 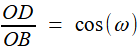 (3) (3)Reportant (3) dans (2) on a 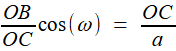 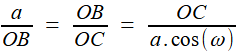 |
|
| Attention! Pas d'euphorie précipitée: dans cette formule, ω varie avec le point B (ou, ce qui revient au même, C); comment pourrait-il en être autrement, puisqu'elle tient pour tous les points de la courbe d'Archytas? Mais si cos (ω) peut prendre, à une certaine position, la valeur b/a, le but sera atteint! De l'intérêt d'avoir supposé au départ que b < a. L'ensemble des points M tels que, H désignant la projection orthogonale de M sur OA, on ait OH = b/a .OM
est un cône de révolution d'axe OA (puisque cela revient à fixer l'angle de la droite OM avec l'axe OA). Dès lors, tout point de la courbe d'Archytas se trouvant aussi sur ce cône réalise la relation souhaitée, faisant de x = OB et y = OC des moyennes proportionnelles intermédiaires entre a et b:
Les formules (que nous vous avons épargnées) permettent de justifier l'existence d'au moins un tel point. Qui, si l'on revient aux surfaces porteuses, se trouve ainsi à l'intersection d'un cylindre, d'un tore à collier nul, et d'un cône de révolution! Bien sûr, si satisfaisante qu'elle fût pour l'esprit, son élégance n'avait d'égale que son impraticabilité; Ératosthène
avait beau jeu de la citer en première position de la liste de celles
qu'il entendait surclasser avec son appareil. Voici l'avis d'un
spécialiste de l'étude des courbes:
|
||
Eudoxe et la Kampile
|
Ératosthène, lettre à Ptolémée III (citée par Eutocius)
|
Eudoxe... de Cnide! Pourquoi ne pas commencer par une visite virtuelle de sa cité natale? Il ne faudrait pas oublier le volet tourisme de nos pages, quand même! De lui n'y subsiste guère qu'un cadran solaire qui lui est attribué, certes, mais l'esprit des lieux, le souvenir de l'Aphrodite de Praxitèle ne sont-ils pas une excellente mise en condition relaxante pour faire un peu de géométrie?
| Cnide
(aujourd'hui Datça, en Turquie): le port de commerce, le cadran, le
port militaire... un petit avant-goût pour vous y inviter! |
||
|
"Eudoxe de Cnide (408-355 av. J. C) [...] s'est signalé par l'invention d'une courbe destinée à la solution du problème de Délos et qu'il appela du terme général de kampyle ( [mot qui signifie] infléchie). Malheureusement Eutocius n'a pas compris la solution d'Eudoxe qui subsistait encore de son temps, et, la trouvant erronée, ne nous l'a pas conservée. On est donc réduit, sur la nature de la kampyle, à des conjectures sans appui.[...]
J'ai supposé [...] qu'il s'agissait de l'une des projections des courbes gauches de la solution d'Archytas. " P. TANNERY, Notes pour l'Histoire des Lignes & Surfaces Courbes dans l'Antiquité,
in Bulletin des Sciences Mathématiques et Astronomiques 2e série, tome 8, n°1 (1884), p. 101-112 |
Il semble que, chez les géomètres grecs, le mot kampyle désignait très généralement une ligne qui n'était ni une droite, ni un cercle, un objet au dessin plus capricieux, dont la courbure pouvait varier, au contraire de la droite et du cercle, pour qui elle est constante. Une courbe qui peut aussi s'infléchir -d'où l'étymologie... Mais Eudoxe l'emploie pour désigner une courbe très particulière.
Commençons par nous dire que si l'on veut trouver une solution sans sortir du plan, il est assez naturel, plutôt que redémarrer de zéro, de songer à partir de la solution de l'espace et de la projeter. Raison supplémentaire: Eudoxe était l'élève d'Archytas, donc bien placé pour connaître sa solution et s'efforcer de poursuivre la route... de nos jours, c'est comme cela que les thésards obtiennent leur sujet. Mais la courbe d'Archytas, parce qu'elle est sur le cylindre, se projette sur son cercle de base, ce qui est peu intéressant: tous les points de la verticale, celui qui est solution comme tous les autres, viennent "s'écraser" sur le même point de ce cercle; impossible dès lors de distinguer celui qui nous intéresse, il faut autre chose.
Voici alors notre stratégie en vue d'une résolution dans le plan: une nouvelle idée peut consister à regarder différemment l'intersection des 3 surfaces, le cylindre (C ),le tore (T ) et le cône (K) :
en coupant la courbe d'Archytas par le cône, nous avons réalisé
Observons que trouver R dans l'espace ou S dans le plan (répondant à leurs spécifications respectives) revient rigoureusement au même: quand on connaît R, sa verticale nous amène en S sur le cercle de base; et si l'on a trouvé S, on monte sur sa verticale jusqu'à rencontrer le cercle méridien du tore en R. Nous avons donc transformé le problème en un problème plan équivalent, et nous aurons ainsi complètement évacué la géométrie dans l'espace... à condition de savoir déterminer et tracer(χ ) .
Cette fois, nous commencerons par le calcul analytique, parce que Tannery indique en note l'équation de la courbe : ce sera le moyen d'être sûr qu'on est en accord avec lui, car il n'a précisé dans sa présentation, ni quelle courbe gauche, ni quelle projection il considérait!
| Et pour les amateurs d'équations ...( bis) On trouve facilement l'équation du cône à partir de sa méridienne dans le plan de base (Ox,Oy), qui est formée de deux droites symétriques par rapport à Ox. Cette méridienne s'écrit
(y - x tan ω ). (y + x tan ω ) = y² -x² tan²ω = y² -x² [ a²/b² - 1] = 0
L'axe de révolution étant Ox, il nous suffit de remplacer y² par y² + z² d'où l'équation de (K ) y² + z² - x² [ a²/b² - 1] = 0 Nous obtenons alors pour la courbe ( Χ ) le système formé par les deux équations (K ) b² ( x² + y² + z² ) - a²x² = 0
(T ) ( x² + y² + z² )² - a²( x² + y² ) = 0 Combinant les deux de manière à éliminer z, on a immédiatement le support de sa projection horizontale... la kampyle (χ ) ! 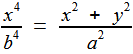 (χ
)
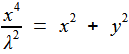 et (χ
) et (χ
) 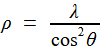
N.B. : support seulement, parce qu'on a éliminé z² et non z; de ce fait, l'existence réelle d'un z correspondant à un point de (χ
) n'est pas garantie. De fait, on va voir que la kampyle a des branches infinies, ce qui n'est pas possible pour ( Χ
), portée par le tore, qui est borné.
|
Un problème historique subsiste toutefois, et de taille: si c'est bien la courbe considérée par Eudoxe, comment a-t-il fait pour la tracer en se passant des équations?
Les considérations analytiques qui précèdent sont chronologiquement hors jeu. Il faut imaginer des constructions géométriques simples permettant un tracé point par point -mais autant que l'on voudra- afin de se faire une idée de l'allure de (χ ).
Voici une possibilité qu'entrevoit le Mathouriste : certes, cela s'apparente à une technique de géométrie descriptive avant l'heure, mais il y a eu d'autres antécédents (Dürer avant Monge, et de manière bien plus poussée que ce que nous allons faire ici). Eudoxe pourrait être le Monsieur Jourdain de cette histoire... Qu'il soit bien clair qu'à l'instar de Tannery, nous propsons là une "conjecture sans appui", un travail qui est dans les moyens d'Eudoxe à son époque, et rien de plus. Si vous avez déjà applati un carton d'emballage (3D) pour le faire rentrer (en 2D) dans votre poubelle, vous disposez de tout le backgroud scientifique pour piger cette construction!
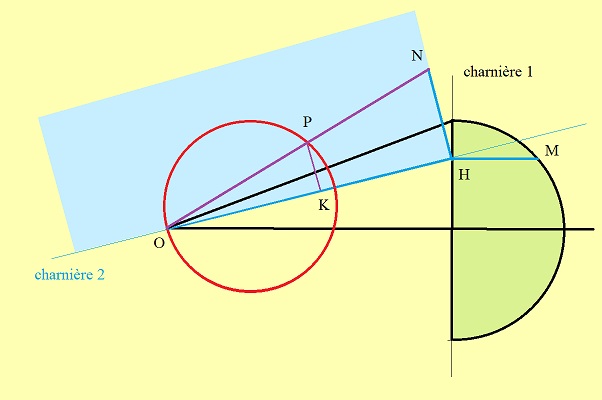 |
L'idée est de couper toute la figure par un plan méridien du tore (vertical), qui pivote autour de (Oz),
comme nous l'avons fait pour étudier la courbe d'Archytas. Ainsi,
autant de positions considérées, autant de points construits des
courbes ( Χ
) et (χ
).
En effet, chacun de ces
plans a une intersection très simple avec chacune des deux surfaces en
jeu: un cercle méridien pour le tore (T ), et un couple de génératrices pour le cône de révolution (K), puisqu'il contient le sommet. Ainsi, dans ce plan auxiliaire (Π
), l'affaire se résume à une intersection droite-cercle.
Le cercle méridien est connu, de rayon fixe et tangent en O à (Oz); le seul travail est donc de construire l'intersection du plan (Π ) avec le cône. On choisit un plan arbitraire (V) perpendiculaire à l'axe de révolution, à la fois Vertical et Vert... d'où son nom. (Π ) le coupe selon une verticale issue du point H. Quand on rabat ce plan sur le plan horizontal, c'est à dire qu'on le fait tourner de 90° autour de "charnière 1", on voit en vraie grandeur HM où, par rotation, M est le point sur la génératrice de (K) qui se trouve dans (Π ). Dans un deuxième temps, on rabat (Π ) -en bleu- autour de "charnière 2" pour lire en vraie grandeur ce qui s'y passe. HM = HN , car M =et N ne font qu'un dans l'espace, ce qui permet de tracer ON, génératrice de (K) qui se trouve dans (Π ). Elle rencontre le cercle méridien -rouge- de (T ) en P, qui est donc un point de ( Χ ) , dont la projection orthogonale K est un point de la kampyle (χ ). |
|
Vous n'avez plus, pour
mieux voir dans l'espace, qu'à découper la figure, et remonter votre
carton d'emballage dans l'espace en pliant suivant les pointillés!
L'ouvrage de Knorr [17] donne une autre explication possible, ainsi qu'un procédé de génération par points (c'est à dire, un moyen de construire des points de la courbe, autant que l'on voudra) . |
|
Ménechme, par les Coniques
|
" [...] Mais à tous il arriva de donner la
démonstration sans qu'ils pussent la réaliser
effectivement et en faire l'application pratique, à l'exception
de Ménechme qui
y réussit un peu, d'une manière
laborieuse."
Ératosthène, lettre à Ptolémée III (citée par Eutocius)
|
Ménechme (circa 380 av. J.-C., circa 320 av. J.-C.) est, selon Apollonius et tous ses suiveurs, l'inventeur des coniques (ou, peut-être devrait-on dire, le découvreur en réalisant les diverses sections du cône) et, toujours selon Eutocius dans ses commentaires d'Archimède, il les a utilisées de deux façons pour résoudre le problème des moyennes proportionnelles. Dit d'une façon moderne, cela consiste à présenter la suite d'égalités
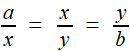
sous diverses formes équivalentes, en groupant différemment les termes 2 par 2. C'est ainsi qu'il propose deux solutions, chacune étant donnée par l'intersection de deux courbes:
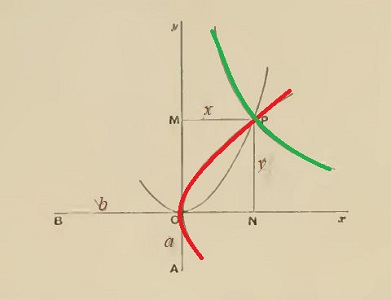
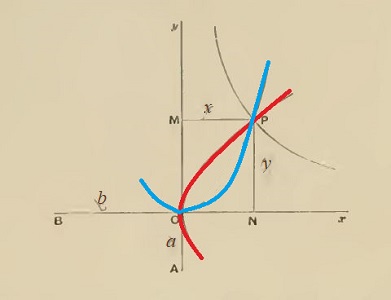
| Solution 1 | Solution 2 |
| a / x = y / b et x / y = y / b | a / x = x / y et x / y = y / b |
| xy = ab et y² = bx | x² = ay et y² = bx |
 |
|
| hyperbole et parabole |
parabole et parabole |
Bien sûr, il n'emploie pas de coordonnées; l'hyperbole, par exemple, est décrite comme ensemble des points laissant constante l'aire du rectangle OMPN, égale à l'aire du rectangle construit sur OB et OA, ce qui se traduit par
En revenant aux rapports, il réalise bien l'égalité demandée, lorsque le point P est à l'intersection des deux courbes -dont l'existence est considérée comme évidente.Bien sûr, on na aucune ma,nière de construire exactement ce point à la règle et au compas; on peut construire exactement autant de points que l'on voudra de ces paraboles, mais tout ce qu'on pourra faire pour déterminer P est une interpolation à vue; c'est sans doute en cela qu'Ératosthène la trouve "laborieuse". Son avantage, par rapport aux deux précédentes, est de faire intervenir les courbes les plus simples après la droite et le cercle.
Statue d'Omar Khayyam au parc Laleh (Téhéran) Dans la douceur d'une nuit persanne... |
Cette solution 2, par intersection de deux paraboles, est aussi celle qu'emploie Omar Khayyam pour résoudre l'équation fondamentale du troisième degré, x3 = c. En effet, tirant y=x²/a de la première et reportant dans la seconde, on a, en écartant la solution triviale x=0, x3 = a²b . Il fait référence explicitement à Apollonius et à l'intercalation de moyennes. Mais s'il se place ainsi dans la continuité des géomètres grecs, il va beaucoup plus loin en étendant la résolution par intersection de coniques à toutes les équations du troisième degré. L'histoire de cette grande première est à retrouver dans notre page spéciale, en compagnie de ses poèmes et de miniatures persannes illustrant une édition iranienne de ses fameuses Rubayyiat. |
N.B. : la Simplicité selon Mersenne
Mersenne, que nous avons déjà vu à l'œuvre sur les moyennes proportionnelles au début du tome 2 de son Harmonie Universelle (voir page précédente),
y revient bien plus loin dans son traité... à propos de l'accord des
orgues! (Livre X); la question reste la même: diviser un intervalle
sonore en parties égales.Il se propose, après avoir expliqué en quoi, selon la tradition ancienne initiée par Pappus, la solution de Ménechme est la plus simple (il cite onze auteurs, mais sans expliciter leurs méthodes), donc est en cela supérieure à toutes les autres et doit leur être préférée... on peut encore faire mieux, et made in France, s'il vous plaît!
Il nous faut, pour suivre son discours, nous initier à son vocabulaire et à sa hiérarchie de complexité, que nous présentons en croissant:
- lieux plans : les droites et les cercles (résolutions par la règle et le compas, donc)
- lieux solides : les autres coniques (ellipse, parabole, hyperbole)
- lieux linéaires : autres courbes (conchoïdes, cissoïdes, spirales, etc... dont nous reparlerons plus loin)
Voici donc son canon esthétique:
| "[...] comme les anciens, au rapport de Pappus, ont estimé que c'estoit une grande faute de résoudre par les lieux solides, ou linaires, un Problème qui de sa nature pouvoit être résolu par les seiuls lieux plans; j'estime semblablement que la faute n'est pas moindre de résoudre par des lieux linaires, ou [...] par des descriptionss à tâtons, un Problème qui de sa nature pouvoit être résolu par par les lieux solides." |
Entendons nous bien (mais avec humour): ce n'est pas une faute mathématique, c'est pire: c'est une faute de goût! Un avis que partage Descartes, dont on peut constater qu'il ne tient pas un langage fondamentalement différent... et que cela conduit à définir les équations des courbes.
C'est donc une condamnation esthétique des solutions à venir par des courbes de degré plus élevés: cissoiïde (3), conchoïde (4), assortie d'un credo qui tout à la fois tient du rasoir d'Ockham et anticipe, par l'appel à la nature, le principe d'énergie minimale:
| "[...] puisqu'à l'imitation de la nature, nous devons tout faire par les moyens les plus simples." |
Mais comme dans sa hiérarchie, employer un cercle est préférable à une conique, il vante, en créditant son auteur, une solution par le couple parabole-cercle plutôt que le couple parabole-parabole de Ménechme:
 |
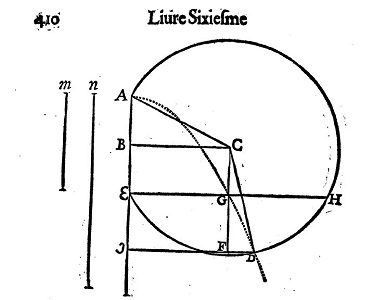 |
| Oui, le célèbre Gilles Personne de Roberval (1602-1675) celui de la balance à deux plateaux... | démonstration complète: pp 410-411 |
 à la Bibliothèquz Sainte Geneviève, Paris |
 |
Descartes reprend l'idée dans la Géométrie, et l'applique à toute équation du troisième degré. Cercle et parabole pour tout le monde!
Le principe de Khayyam simplifié, en somme (grâce à la considération de coefficients négatifs, ce qui évite la prolifération des cas), mais pas mal d'années après. |
| On
remarque que le problème des moyennes proportionnelles (mais aussi,
plus loin, la trissection de l'angle) est explicitement mentionné comme
cas d'application. |
Nicomède et la Conchoïde
Dioclès et la Cissoïde
( La suite en
construction... )



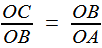 , soit
, soit 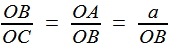 (1)
(1)
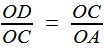 , soit
, soit 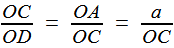 (2)
(2)