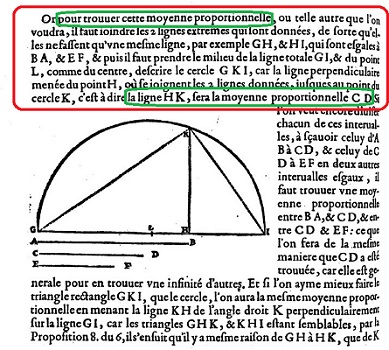
Solutions par des Machines


Platon Mécanicien ? 

C'est encore Eutocius, le transcripteur de la lettre d'Ératosthène (voir la page précédente) qui prête à Platon la première idée d'une machine destinée à résoudre la question des moyennes proportionnelles, c'est à dire construre deux .longueurs x et y vérifiant, pour les longueurs a et b données: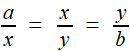

Il s'appuie sur la figure suivante, où les angles entre les droites rouges , en H et K, sont supposés droits; en ce cas, l'égalité à prouver est réalisée avec a, b, x, y positionnés comme indiqué sur la figure; et on va le montrer grâce à un lemme très simple sur les triangles rectangles. Et très utile, on va le voir...
La Propriété
 Le Lemme



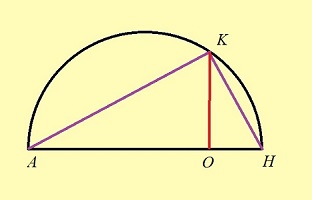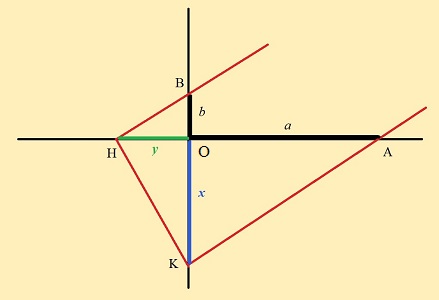
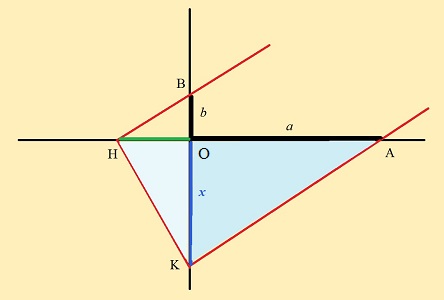
 Lemme : On soppose le triangle AKH rectangle en K. (Le cercle évoque ce fait par une propriété bien connue, mais elle ne sera pas utilisée ici; nous la retrouverons... pour la solution par des courbes, en page suivante!).
                 Alors, OK / OA = OH / OK

 >  Preuve: les angles OAK et OKH sont égaux, parce qu'ils ont leurs côtés perpendiculaires (importance de l'angle droit en K!). Donc les triangles, rectangles OAK et OKH sont semblables, d'où l'égalité à prouver. On peut aussi dire que les deux angles égaux OAK et OKH ont donc la même tangente, exprimée par ce rapport. <

et, savez vous où l'on peut le retrouver, ce lemme? Dans le deuxième tome de ce qui est sans doute le premier grand traité de musique, l'Harmonie Universelle du père Marin Mersenne. Et cela ne surprendra pas les mathématiciens ou les physiciens, mais seulement, comme l'écrit le bon père, "ceux qui ne sçavent pas la géométrie".

Car diviser un intervalle musical en deux intervalles égaux, c'est exactement insérer une fréquence nouvelle entre deux fréquences données, et, parce que notre perception s'organise autour des rapports de fréquences, de telle manière que
 f2 / f = f / f1 .

C'est à dire, un problème de moyennes proportionnelles! Puis diviser en 3 requerra deux moyennes proportionnelles -comme notre problème de duplication du cube. Quant à la division de l'octave en douze intervalls égaux (qui fut envisagée, à défaut d'être retenue)... comptez vous-même!

ci-contre: le père Mersenne à l'écoute de Desargues, pendant que Descartes discute avec Pascal (de dos)
Peinture murale à la Sorbonne (Paris), et tous les détais sur ce quatuor dans notre page dédiée.





l'ouvrage de Mersenne extraits  des pages 65 et 66 du traité, consacrées à ce lemme.
 
Preuve de la propriété des moyennes proportionnelles :
> On applique deux fois de suite ce sympathique petit lemme!
 
Appli n°1
 Appli n°2




Une première fois, dans le triangle AHK pour établir, en considérant les deux triangles bleus, 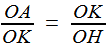, soit  ;
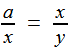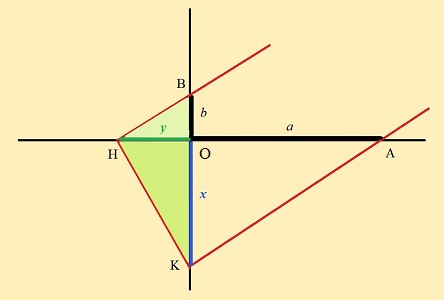
une deuxième fois, dans le triangle KHB pour établir, en considérant les deux triangles verts, 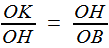 , soit .
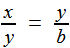On peut remarquer qu'une seule application fournissait un moyen d'extraire la racine carrée d'un nombre a (en ce cas, se donner y=1). Ainsi, l'idée d'insérer une deuxième égalité similaire devient assez naturelle, et c'est sans doute à partir de ce constat qu'elle est venue à Hippocrate de Chios (mais nous n'avons, de lui, aucun texte pour le confirmer).
Les deux égalités s'enchaînent pour donner le résultat désiré. <

Application effective : le plus rudimentaire, et probablement ce qui fut fait à l'époque, est d'utiliser deux équerres de charpentier que l'on fait coulisser l'une sur l'autre, de manière à placer leurs angles droits respectifs sur les axes tout en les faisant passer par les points A et B donnés.
On peut par exemple "essayer" n'importe quelle position de H tout en mainteant le passage par B donné, voir le point K obtenu et y poser la deuxième équerre, avec un côté sur HK. L'autre coupera l'axe des abcisses en "ratant" le point A (sauf miracle de chance!), et on tentera de modifier la position de H pour s'approcher de A, qui est fixe...

Travaux pratiques conseillés (mais oui!) : le meilleur moyen de voir que ce n'est pas si facile -même pour trouver à peu près la solution- c'est d'essayer vous-même: portez a et b sur des axes perpendiculaires, et découpez dans un carton un peu épais les deux équerres (en forme de "L" épaissi). Et essayez de remplir toutes les conditions!
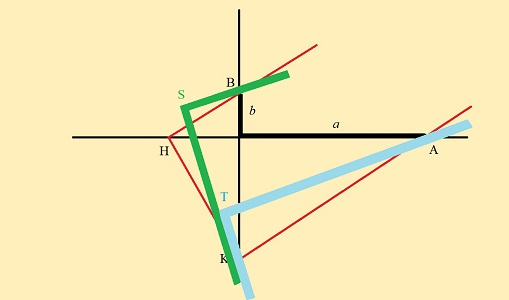
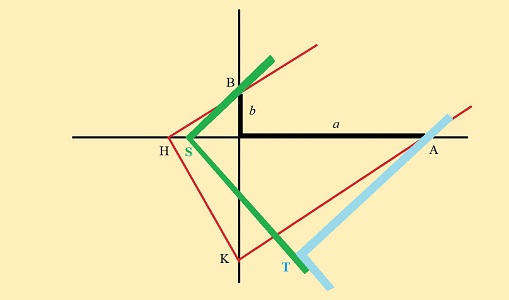
Voici deux exemples où ça bloque après avoir satisfait une partie des contraintes; l'équerre bleue coulisse sur la verte, leurs côtés restant collés selon une même direction :
Ratage n°1
 Ratage n°2

 
Ici, on a veillé à faire passer un bras de la verte par B, un bras de la bleue par A, mais du coup on a raté le positionnement de S et T sur axes.
 Là, on a fait passer un bras de la verte par B, tout en positionnant le sommet S sur l'axe des abcisses.
Mais alors, ou on fait passer un bras de l'équerre bleue par A, et on rate le positionnement de T sur l'axe (ci-dessus), ou on fait glisser l'équerre bleue sur la verte pour amener T sur l'axe des ordonnées... et on rate le passage par A! (ci-dessous)



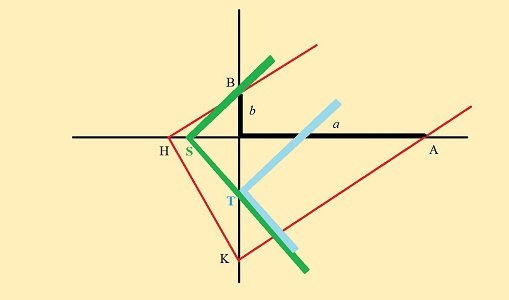Ainsi l'on constate qu'il n'est pas possible de fixer la position d'une équerre d'abord, puis de faire coulisser l'autre; il faut vraiment les bouger simultanément! À vous de conclure après votre petite séance expérimentale sur la commodité du procédé. Certes, avec un peu d'entraînement, on parviendra à quelque chose d'acceptable... à la précision d'un charpentier, mais certainement pas d'un géomètre grec dont l'éthique exige une construction exacte aux instruments.

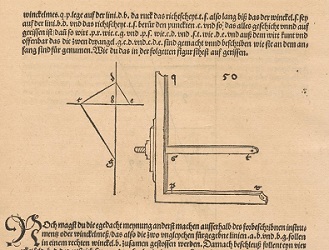
Platon "son" appareil
(dans une version moderne du Musée de Modène)		 le premier réalisateur supposé, Albrecht Dürer
Underweysung der Messung, p168;
à voir intégralement sur la bibliothèque numérique e-rara


Mais justement, cette solution mécanique est-elle bien en phase avec l'idéal platonicien? Il est permis d'en douter, et encore plus si on lit ce commentaire de Plutarque (1er siècle après J.-C.):
"Les premiers essais de cette mécanique si prisée et si vantée sont dûs à Eudoxe et Archytas, qui voulurent agrémenter joliment la géométrie et appuyer par des expériences sensibles et instrumentales des problèmes qu'il n'est pas facile de résoudre par une démonstration logique et géométrique. Tel est le problème des deux moyennes proportionnelles. [...] Tous deux l'appliquèrent à des instruments appelés mésographes [...]
 Mais Platon s'indigna et leur reprocha énergiquement de perdre et ruiner l'excellence de la géométrie, qui désertait avec eux les notions abstraites et intelligibles pour passer aux objets sensibles et revenait à l'utilisation d'éléments matériels, qui demandent un long et grossier travail manuel. La mécanique déchue fut ainsi séparée de la géométrie, et longtemps méprisée par la philosophie, elle devint une branche de l'art militaire."
Plutarque, La Vie de Marcellus in Les Vies des hommes illustres

Il se peut donc qu'Eutocius  ait fait un contresens en attribuant à Platon ce que ce dernier fustigeait. D'un autre côté, nous verrons, à la page suivante, les noms de ces deux mathématiciens accolés des solutions par des courbes, mais sans allusion aucune à un moyen mécanique associé: est-ce, cette fois, Plutarque qui mélange auteurs et procédés? Et peut-être aussi Eudoxe et Ératosthène, à en croire l'allusion au mésographe, que nous présentons ci-dessous... Malheureusement, nous manquons cruellement de documents qui viendraient éclaircir cette zone d'ombre.

Le mésolabe d'Ératosthène

Il s'agit de l'appareil tant vanté à Ptolémée. Comme l'astro-labe permet (étymologiquement) d' "attraper les étoiles", le méso-labe permet... d'attraper les moyennes!


"L'instrument construit est une plaquette de bois, d'ivoire ou de bronze comportant trois tablettes égales aussi minces que possible. Celle du milieu est fixe, les autres peuvent être déplacées dans des rainure. [...] Il faut veiller avec soin à ce que, dans le déplacement des tablettes, tout reste parallèle et que les différentes pièces soient parfaitement ajustées."
Érathosthène, Lettre à Ptolémée


a et b étant donnés, il s'agit de placer les trois triangles égaux (rouge, vert, bleu sur le schéma de principe) de manière à aligner les points d'intersection "hauteur/hypothénuse du suivant" le long de la "ficelle" (jaune sur le schéma). La figure comporte alors deux jeux de triangles homothétiques (le centre de l'homothétie  est  le point d'intesection entre les droites noire et jaune, en bas et à droite), ce qui conduit facilement à la réalisation des moyennes proportionnelles. 


Le mésolabe (réalisé au Musée de Modène)  Son principe: réaliser les Moyennes Proportionnelles
 
                          

Il faut reconnaître que, dans l'optique d'une détermination pratique, l'appareil est techniquement réussi, bien plus simple et plus prompt à donner le résultat que le jeu avec deux équerres.
[démonstration animée au Musée de Modène, étude approfondie (en Italien)]

Un certain Descartes

statue de Descartes
Institut de France, Paris
 		Discours de la Méthode, édition originale (1637)
La Géométrie en est une annexe de mise en application de la Méthode...
Arithmeum, Bonn (Allemagne)
 Descartes, La Géomtrie, édition séparée(italienne)  avec commentaires
Arithmeum, Bonn (Allemagne)

Dans le Livre II, Descartes s'intéresse en priorité aux courbes. S'il revient sur les inventions des Grecs, il n'y mentionne pas explicitement la duplication du cube, ni même l'intercalation de moyennes proportionnelles entre deux longueurs données. Ce qui l'intéresse à ce stade, ce sont les courbes décrites par D, F et H (en pointillés sur sa figure), dont il affirme qu'elles sont "de plus en plus composées" ; traduisons; "de degrés de plus en plus élevés", 4 pour D, 8 pour F... ou "utilisant de plus en plus d'équerres", le mot composé n'étant pas clairement défini.




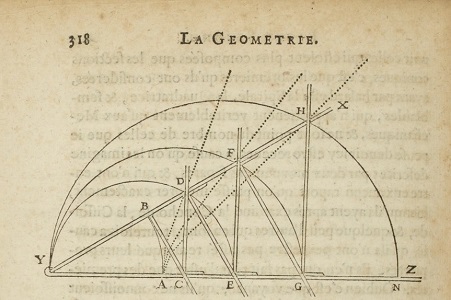Le bras YZ est fixe, YX mobile, en rotation de centre Y. En ouvrant de plus en plus l'angle entre eux, B, qui est fixe, décrit un cercle, et BC, perpendiculaire à YX, pousse le pied C de la verticale CD, qui pousse à son tour la parallèle DE à BC, etc...La ressemblance avec le le mésolabe -que Descartes connaissait- saute aux yeux: deux familles de triangles, et le même jeu de similitudes; d'ailleurs Descartes explicite la succession des rapports égaux.
Donc l'appareil est apte à résoudre le problème des moyennes proportionnelles, et il y vient dans le Livre III, affirmant en toute modestie qu'il n'y a pas de façon plus facile... que d'employer son appareil! Qu'il n'a pourtant jamais construit ou fait construire, à ce que l'on sait; pourtant, indéniablement, l'ajustement par un mouvement continu évite le tâtonnement inhérent au mésolabe (l'alignement de points sur la ficelle).





 C'est l'occasion de discourir sur la simplicité des moyens à mettre en œuvre pour résoudre un problème donné. Fort bien, fort louable, encore faudrait-il être plus clair sur le mot genre (s'agit-il du degré, lorsqu'ensuite il va mettre ses courbes en équations?). Simplicité de la courbe elle-même, apparamment, non de son appareil traceur ou de la facilté qui en résultera pour le problème étudié... C'est une question qui avait donné lieu à des échanges avec Mersenne, et plus tard à l'opposition de Newton et Leibniz, partisans quant à eux des critères repoussés par Descartes.

Puisque c'est une affaire qui touche aux courbes plus qu'aux machines, nous y reviendrons dans la page suivante... mais en fait, on y découvrira un lien, a priori surprenant, entre courbes et machines.






Revenir à la Home Page du Mathouriste