| modèle (x² +
y² +z² + R² - r² )² - 4R² (x² +
y² )=
0 |
Mais, en termes de
génération, c'est ce qu'il y a de
plus simple
après... la sphère! On fait toujours tourner un
cercle de
rayon r,
mais, au lieu de
prendre pour axe de révolution un diamètre, on
dépalce celui-ci parallélement à
lui-même
d'une distance R.
Le
résultat obtenu est une forme plus familière
à
beaucoup de non mathématiciens que les quadriques
propres:
un pneu, une bouée, un bracelet vous en font voir tous les
jours.
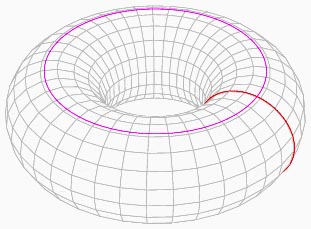
de l'article Tore de Wikipedia
de l'article Tore de Wikipedia
Cette surface est
d'ailleurs connue
depuis l'antiquité Grecque: Perseus est
crédité le
premier de l'étude de ses sections planes (vers 250 avant
J.-C.), et Archytas de Tarente (IVème
siècle avant J.-C.) y fait implicitement appel dans sa
solution de la duplication du cube!
Qu'il se fasse élément de décoration ou élément de maçonnerie, c'est d'abord comme "forme naturelle" que le tore s'introduit dans les monuments...
Milet (Turquie): aspect général du théâtre
Milet: les couloirs, vue intérieure
Milet: les couloirs, vue supérieure
Rome (Italie): théâtre de Marcellus (13 avant J.-C.)
Rome (Italie): intérieur du Colisée(70-80 après J.-C.)
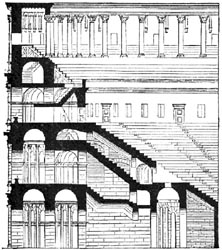
Coupe du Colisée montrant les vomitoires (source : Wikipédia)
Qu'il se fasse élément de décoration ou élément de maçonnerie, c'est d'abord comme "forme naturelle" que le tore s'introduit dans les monuments...
Le Tore Décoratif
Il est présent à la base des colonnes des temples; plus exactement la portion engendrée par le demi-cercle "extérieur" vient elle border un dique plein qui soutient la colonne; il peut d'ailleurs recevoir une décoration à motifs répétitifs. |
 |
 |
| Aphrodisias (Turquie) | Didymes (Turquie), temple d'Apollon | Didymes (Turquie) |
Une telle
maîtrise dans la facture témoigne qu'il s'agit de
monuments relativement tardifs - IIIème
siècle avant J.-C. pour Didymes, IIème
siècle avant J.-C. pour Aphrodisias; on pourra
vérifier que dans les temples "archaïques" du Vème
siècle avant J.-C. (Ségeste, Agrigente en Sicile,
par
exemple), le fût est posé à
même le sol. En
revanche, la colonne Romaine adoptera ce style de base.
Et bien sûr, c'est la forme idéale pour un bracelet... témoin, ce superbe exemple, d'origine Carthaginoise.
Musée du Bardo, Tunis
Et bien sûr, c'est la forme idéale pour un bracelet... témoin, ce superbe exemple, d'origine Carthaginoise.
Musée du Bardo, Tunis
Les Voutes Toriques
De la Grèce à Rome
Cette fois, place à un tore géant! Le plus ancien site nous vient du Monde Grec, à Milet, patrie de Thalès (aujourd'hui en Turquie);il est plus que probable que les couloirs de circulation situés en dessous, dont le plafond constitue naturellement un demi-tore, proviennent de la transformation Romaine ( IIème siècle après J.-C.) du site créé au IIIème siècle avant J.-C. En effet, l'accès aux théâtres Grecs se faisait toujours extérieurement, par les gradins; ces vomitoriums, ou vomitoires, sont une invention des Romains.
Milet (Turquie): aspect général du théâtre
Milet: les couloirs, vue intérieure
Milet: les couloirs, vue supérieure
On retrouvera la
même forme de
voute dans les théâtres Romains, qui conservent le
plan en
demi-cercle hérité de la Grèce (sans
toutefois
s'adosser à une colline, comme on le voit ci-dessous).
Rome (Italie): théâtre de Marcellus (13 avant J.-C.)
On observe nettement,
à droite, la section semi-circulaire engendrant le (demi-)
tore par rotation. Le théâtre a un
diamètre (extérieur) de 111m, tandis que cette
galerie est large de 2 à 3m: notre qualificatif de tore
géant n'est donc en rien usurpée!
À titre de comparaison, puisque les accélérateurs de particules ont une chambre torique (mais bien moins facile à visiter...), le Cosmotron, premier synchrotron construit (1953) avait un diamètre de 23m environ (anneau); celui de la section était de quelques dizaines de centimètres. Bien sûr, on a fait beaucoup plus grand depuis: anneau du CERN à Genève (diamètre de 8,6 km) mais l'ordre de grandeur est comparable à l'ESFR de Grenoble (diamètre 320m).
[voir une liste des accélérateurs]
On peut aussi comparer au plus grand tokamak actuel, le JET (Joint European Torus, le titre est on ne peut plus explicite) dont les deux rayons sont 2,96m et 1,25m... (en n'oubliant tout de même pas que le record visé par tous ces beaux appareils concerne l'énergie, pas la taille!)
la chambre torique du Jet, vue de l'intérieur:
cliché EDF-JET mis à disposition de Wikipédia
À titre de comparaison, puisque les accélérateurs de particules ont une chambre torique (mais bien moins facile à visiter...), le Cosmotron, premier synchrotron construit (1953) avait un diamètre de 23m environ (anneau); celui de la section était de quelques dizaines de centimètres. Bien sûr, on a fait beaucoup plus grand depuis: anneau du CERN à Genève (diamètre de 8,6 km) mais l'ordre de grandeur est comparable à l'ESFR de Grenoble (diamètre 320m).
[voir une liste des accélérateurs]
On peut aussi comparer au plus grand tokamak actuel, le JET (Joint European Torus, le titre est on ne peut plus explicite) dont les deux rayons sont 2,96m et 1,25m... (en n'oubliant tout de même pas que le record visé par tous ces beaux appareils concerne l'énergie, pas la taille!)
la chambre torique du Jet, vue de l'intérieur:
cliché EDF-JET mis à disposition de Wikipédia
Le "Problème" des Amphithéâtres... encore!
Et si on remplace le théâtre circulaire par un amphithéâtre elliptique? Retournons au Colisée de Rome, déjà évoqué à la page Cylindres & Cônes. On peut y voir des galeries de circulation voutées du même type. La vue centrale, malgre les échafaudages, a au moins l'intérêt de situer la position de ces couloirs par rapport au cône des gradins, partiellement reconstitué..
Rome (Italie): intérieur du Colisée(70-80 après J.-C.)
Coupe du Colisée montrant les vomitoires (source : Wikipédia)
Et si nous disons que le
problème de la forme esr reposé de facto, c'est
que... si
la courbe lieu des centres des cercles (formant les sections de la
voute) est une ellipse, les exrémités des
diamètre
décriront, eux, des courbes
paralléles à l'ellipse!
Ôtons d'emblée des illusions aux naïfs:
ce ne sont
pas des ellipses, mais des courbes de degré 8
appelées toroïdes.
Toutefois, si l'ellipse a été approchée par une quadrarc de Serlio, c'est à dire une succession de 4 arcs de cercle, nos couloirs sont autant de portions toriques mises bout à bout... et le tore reste bien présent, pluôt que d'avoir recours à une surface notablement plus compliquée.
Insistons enfin sur le fait que la différence entre ellipse et quadrarc, mesurée sur le rayon de courbure à l'ellipse, n'excède pas 1,5%. Elle n'est donc évidemment pas appréciable à l'œil nu... pour ne rien dire sur les "tolérances" qui sont d'usage, encore aujourd'hui, dans le bâtiment!
Des couloirs à voute cylindrique "alimentaient" cet anneau de circulation. De sorte que dans un bâtiment intact, on aurait sans doute pu admirer une intersection tore-cylindre (courbe de degré 8)... dont il nous semble voir une esquisse à l'endroit fléché.
Toutefois, si l'ellipse a été approchée par une quadrarc de Serlio, c'est à dire une succession de 4 arcs de cercle, nos couloirs sont autant de portions toriques mises bout à bout... et le tore reste bien présent, pluôt que d'avoir recours à une surface notablement plus compliquée.
Insistons enfin sur le fait que la différence entre ellipse et quadrarc, mesurée sur le rayon de courbure à l'ellipse, n'excède pas 1,5%. Elle n'est donc évidemment pas appréciable à l'œil nu... pour ne rien dire sur les "tolérances" qui sont d'usage, encore aujourd'hui, dans le bâtiment!
Des couloirs à voute cylindrique "alimentaient" cet anneau de circulation. De sorte que dans un bâtiment intact, on aurait sans doute pu admirer une intersection tore-cylindre (courbe de degré 8)... dont il nous semble voir une esquisse à l'endroit fléché.
Il ne restera donc plus
qu'à découvrir... un
amphithéâtre en meilleur état. Et le
Mathouriste recevra avec un
plaisir gourmand les suggestions de ses lecteurs, pour vous en montrer
encore plus un jour prochain!
Mais au fait, ça ressemble à quoi, une section bitangente ?
C'est facile... en théorie. En pratique, bonne chance, mais vous allez forcément comprendre... ce que vous devriez obtenir; la suite ne dépend que de votre adresse. Prenez un superbe tore, bien appétissant, oui, celui-ci, sur le sommet de la pile:
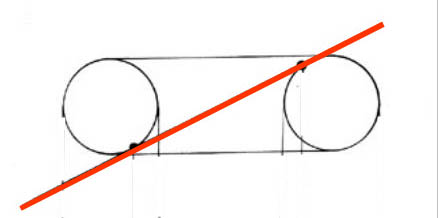
Puis, passez une lame de couteau à travers l'anneau, en lui faisant toucher le beignet dessus et dessous, comme sur ce schéma. Vous n'avez plus qu'à couper dans cette direction, de part en part du tore: sous vos yeux, deux cercles sécants! (dans le plan rouge, celui de la lame) À vous de jouer...
Quel rapport avec le tourisme et l'architecture? De tels cercles sont visibles sur l'escalier en colimaçon du Musée de l'Œuvre Notre Dame, à Strasbourg (attenant à la Cathédrale).
Photo tirée de l'article de Marcel Berger pour BibNum. Cette découverte l'avait surpris et émerveillé...
Et ce qui est hautement remarquable, c'est que cette sculpture a été réalisée par Thomas Uhlberger, vers 1580: l'artiste a précédé le mathématicien!
Yvon Villarceau (1813-1883) était essentiellement un astronome. On ne sera donc pas surpris de trouver la rue qui lui rend hommage, à Paris, à proximité de celles dédiées à Copernic et Galilée.
Un inconscient a garé son scooter sous la plaque, exposant ses pneus aux lames avides d'expériences géométriques amusantes...
Les Sections Circulaires du Tore: une Géométrie... à déguster!
L'image d'accueil de cette page mettait en évidence deux familles de cercles "immédiates", que l'on peut appeler méridiens et parallèles, par analogie avec la sphère terrestre: Mais il y en a deux autres familles, moins évidentes... pour ne pas dire: bien cachées! On les obtient en coupant le tore par un plan bitangent, et c'est le théorème de Villarceau (1848), que Marcel Berger, fasciné depuis son enfance par ce résultat, vous présente sur BibNum en commentant et développant le minuscule article (une demi-page!) de l'auteur.Mais au fait, ça ressemble à quoi, une section bitangente ?
C'est facile... en théorie. En pratique, bonne chance, mais vous allez forcément comprendre... ce que vous devriez obtenir; la suite ne dépend que de votre adresse. Prenez un superbe tore, bien appétissant, oui, celui-ci, sur le sommet de la pile:
Puis, passez une lame de couteau à travers l'anneau, en lui faisant toucher le beignet dessus et dessous, comme sur ce schéma. Vous n'avez plus qu'à couper dans cette direction, de part en part du tore: sous vos yeux, deux cercles sécants! (dans le plan rouge, celui de la lame) À vous de jouer...
Quel rapport avec le tourisme et l'architecture? De tels cercles sont visibles sur l'escalier en colimaçon du Musée de l'Œuvre Notre Dame, à Strasbourg (attenant à la Cathédrale).
Photo tirée de l'article de Marcel Berger pour BibNum. Cette découverte l'avait surpris et émerveillé...
Et ce qui est hautement remarquable, c'est que cette sculpture a été réalisée par Thomas Uhlberger, vers 1580: l'artiste a précédé le mathématicien!
Yvon Villarceau (1813-1883) était essentiellement un astronome. On ne sera donc pas surpris de trouver la rue qui lui rend hommage, à Paris, à proximité de celles dédiées à Copernic et Galilée.
Un inconscient a garé son scooter sous la plaque, exposant ses pneus aux lames avides d'expériences géométriques amusantes...
En guise de conclusion...
Terminons sur une question pratique: vous ne savez sûrement comment ranger vos tores... Aussi, le le Mathouriste a déniché pour vous la solution idéale, à Istanbul (où avaient déjà été photographiés les tores proposés ci-dessus à vos couteaux):