Apollonius de Pergé, section souvenir(s)

( Conics' Trip)

Apollonius (262 avant J.C.- 190 avant J.C., dates approximatives) a beau être l'un des mathématiciens grecs les plus renommés, on ne sait pratiquement rien de sa vie, si ce n'est son lieu de naissance, grâce à l'usage par lequel on distinguait les personnages homonymes en précisant leur origine géographique. Ainsi, par exemple, on ne risquait pas de confondre le mathématicien Hippocrate de Chios avec le célébrissime médecin Hippocrate de Cos; de même plusieurs célébrités historiques portaient le nom d'Apollonius... sans compter les autres.

     Exemple d'homonymie: stèle funéraire portant l'inscription: "à Apollonius, fils d'Alexandre, adieu!"
Musée archéologique d'Arfyon (Turquie)

Même en restant dans le cadre de la science, l'homonymie n'est pas à exclure. Ainsi, alors qu'il est courament considéré comme l'inventeur du système déférente - épicycle développé par Ptolémée, R. d' Hollander (Sciences Géographiques dans l'Antiquité, I.G.N.) n'exclut pas que référence soit faite à un autre, à savoir Apollonius Myndien, qui aurait vécu une cinquantaine d'années auparavant. Pourtant, Ptolémée se conforme à l'usage, en précisant son lieu de naissance, mais ne pourrait-il pas avoir lui-même confondu deux homonymes? Cette mention apparait lorsqu'il présente le mouvement rétrograde des planètes (Mars, par exemple)
"Plusieurs mathématiciens, et parmi eux Apollonius de Pergé, ont étudié une des deux inégalités, à savoir celle qui dépend de la position relative du soleil; s'ils l'ont représenté au moyen de la théorie épicyclique, ils ont fait se mouvoir l'épicycle dans le sens direct du zodiaque, tandis que l'étoile décrit l'épicycle  à une  vitesse égale à celle de l'anomalie... ."
Ptolémée, Syntaxe, Livre XII
C'est donc par ses commentateurs (principalement Eutocius, mais aussi Pappus) que l'on connait cet unique élément biographique. Pappus précise en outre qu'il a longtemps étudié auprès des disciples d'Euclide à Alexandrie, mais on ignore à quel âge il quitta sa ville natale pour se rendre dans cette cité où il est également décédé.

LE traité fondateur de la Théorie des Coniques, source principale de sa célébrité.
Cette édition reprend le fronstispice de la traduction de Halley, montrant des naufragés rassurés, en s'échouant
sur une plage, d'y voir tracées des coniques: "Ouf! Nous sommes chez des civilisés", disent-ils en substance....  

A Pergé... qu'espérer?

Visiter un beau site antique est toujours agréable; mais on ne peut ici espérer voir des  traces de notre homme, à la fois par manque total d'informations sur sa vie, et par le peu d'éléments subsistant de l'époque hellénistique, la sienne: la majeure partie des ruines visibles aujourd'hui sont d'époque romaine (II ème siècle après J.C.).

(source: Wikipedia)

Sur la côte sud de la Turquie, dans une région dénommée à l'époque Pamphylie et non loin d'Antalya, le site de Pergé (prononcer: "Pergué"!) est installé en retrait (17km) de la mer. Il s'organise autour d'une longue voie à colonnes comportant un aqueduc central dont le but est d'alimenter un beau nymphée, au fond.

la longue voie à colonnes (depuis l'entrée du site); la porte hellénistique, un des rares vestiges d'époque grecque.
A l'entrée, le panneau de présentation mentionne Apollonius comme plus illustre personnage de la ville, "célèbre pour avoir été le premier à étudier les propriétés des ellipses" et "précurseur de la théorie planétaire de Ptolémée". La première expression est sans doute un peu approximative, puisque loin de se limiter à l'ellipse, il a fait l'étude de toutes les coniques, et qu'il n'est pas vraiment le premier: c'est Ménechme (380 avant J.C.- 320 avant J.C. environ) qui les introduisit pour résoudre le célèbre problème de Délos, une solution devant laquelle  Ératosthène (276 av J.-C., 194 av J.-C.) faisait quelque peu la moue:  "Ménechme y réussit un peu, d'une manière laborieuse."
Mais restons indulgent: il n'est déjà pas fréquent qu'un site archéologique mentionne un mathématicien! Et voilà que lle long de cette voie, les Dieux ont fait un signe au Mathouriste: une colonne s'est brisée avec une section impeccablement plane, illustrant, sinon la section du cône, du moins celle du cylindre de révolution, inscrivant en ces lieux une ellipse commémorative!



sous tous les angles... et même sous le regard complice d'Artémis, particulièrement vénérée dans la cité.
à moins qu'il ne s'agisse d'un discret rappel de la contribution d'Apollonius à la théorie Ptoléméenne?
Une autre colonne, fracturée aussi nettement suivant un plan, suggère toutefois une explication mécanique, le sectionnement selon une strate du marbre. Si c'est le cas, soyons heureux que les colonnes aient été taillées en oblique par rapport à celles-ci!

Une planéiété proche de la perfection...
Et il y a de quoi inspirer des architectes d'aujourd'hui!

Aquarium à New-Orleans, Louisiana (U.S.A.)
...ou d'hier, comme en témoigne cet angle d'une maison: l'angle du mur est coupé à 45° pour y inscrire une horloge. La partie concave est un cylindre de révolution, d'axe horizontal, à 45° sur chacun des pans de murs... qui offrent donc une section elliptique à notre regard.

Vieille ville de Varsovie, angle de la place du marché et de la rue Zapiecek

Le Traité des Sections Coniques

Rome, unique objet de mon ressentiment...

On nous  présentait autrefois, à l'École Primaire, Rome et la Grèce comme père et mère de notre civilisation. Le propos était laudatif... mais on avait singulièrement "oublié" les côtés sombres de cette hérédité: ni plus ni moins, en matière scientifique, qu'une douzaine de siècles de stagnation et de régression! Car non seulement les Romains n'ont rien fait pour les Mathématiques - d'ailleurs, que peut-on espérer d'un peuple dont le système de numération fait de la moindre addition une épreuve redoutable? - mais, indifférents à ce trésor, ils n'ont même pas été capables de nous conserver l'héritage Grec, dilapidé, perdu, égaré... Et quand l'Empire s'est effondré, la domination chrétienne et la chappe papale ont pris le relais et maintenu l'ignorance acquise: il y eut de grands érudits... mais pas en Sciences. Pendant ce temps-là, la civilisation de l'Islam, partie de rien (une conquête foudroyante par des tribus nomades analphabètes), retrouvait, sauvegardait et prolongeait la Science Grecque. C'est donc du monde arabe qu'elle devait nous revenir...

L'histoire du Traité des Sections Coniques d'Apollonius est  une illustration exemplaire de cette loi générale. Il était composé de 8 livres, dont seul les 4 premiers nous sont parvenus directement, et fort tardivement: la première traduction du grec au latin ne fut entreprise qu'en 1537, à Venise.  Un orientaliste de Leyde, un certain Golius, ramena en 1644 , pour la première fois en Europe, l'ensemble des 7 premiers livres, et les signala au père Mersenne: cette version arabe semble avoir été entreprise dès 830, dans le cadre de la célèbre Maison de la Sagesse du calife Al-Mahmoun, par les  frères Banu Musa  (IX ème siècle ) pour les 4 premiers livres -ceux qui étaient connus- complétée par Thabit Ibn Qurra (836-901) pour les 3 suivants, et soigneusement révisée par Nasir al Din al Tusi vers 1250. Mais, en dépit de l'obtention ou de la découverte d'autres exemplaires arabes, la première traduction/édition de l'ensemble ne se fit qu'à partir de 1706, sous la direction d'Edmund Halley.  Le huitième livre n'a jamais été retrouvé par les Arabes, et Halley en tenta une restitution, d'après descommentaires et des figures trouvées dans Pappus.


Exemples de pages du traité d'Apollonius en Arabe

Mais au fait, comment savait-on le nombre de livres? Fort simplement, par Apollonius lui-même, dans son introduction au Livre I:
"Apollonios salue Eudème.
[... ]
À l'époque où nous nous fréquentions à Pergame, je pouvais constater le vif désir que tu avais de prendre connaissance des travaux que j'avais conduit sur les Coniques ; c'est pourquoi je t'envoie le premier livre après correction, et te ferai tenir les autres lorsque j'en serai satisfait.
Je t'avais dit, et je ne pense pas que tu l'aies oublié, que j'avais entrepris de traiter cette matière à la demande du géomètre Naucatrès, quand il était venu à Alexandrie pour suivre mon enseignement; je t'avais dit aussi que j'avais traité le sujet en huit livres, dont je m'étais dépêché de lui donner communication sans les avoir corrigés, parce qu'il devait prendre le bateau, et que j'avais simplement mis par écrittoutes les idées qui m'étaient venues, dans l'intention d'y revenir plus tard.

Saisissant l'occasion qui m'est offerte maintenant, je rends publique la version corrigée au fur et à mesure de son achèvement."

Autre point intéressant, il délimite clairement sa part d'innovation: les quatre premiers livres sont essentiellement une compilation de résultats plus où moins connus, tandis que la suite est entièrement originale. Ce qui ne veut pas dire qu'il n'y a pas mis beaucoup de lui: comme Euclide pour les fondements de la Géométrie (voir l'emploi du mot éléments), il organise méthodiquement et complète un corpus de résultats épars, introduit le vocabulaire qu'il fixe définitivement, qu'il s'agisse du nom des sections, des diamètres, etc...
"Sur les huit livres, les quatre premiers rentrent dans l'exposition des éléments. Le premier comprend le mode de génération des trois sections et des sections opposées, ainsi que leurs propriétés fondamentales, qui font l'objet d'un traitement plus détaillé et plus général que sous la plume des autres auteurs."

Jeter les bases: le Livre I

La définition est donc posée de manière unifiée par l'étude des sections planes du cône de révolution, d'où le titre de l'ouvrage; plus tard, Sections Coniques sera abrégé en Coniques. La Proposition 1 pésente le cas de la parabole, la Proposition 2 celui de l'hyperbole (ou plutôt d'une branche d'hyperbole, le cône étant limité à sa nappe inférieure), la Proposition 3 celui de l'ellipse. L'hyperbole complète apparaît à la  Proposition 4, sous le nom de sections opposées.


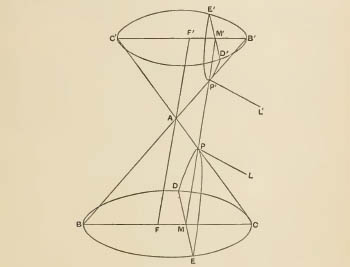figures des propositions 1,3,4 du Livre I (édition anglaise, Heath, 1896)

Cette défintion, le touriste, qu'il soit mathématicien ou non, a bien des occasions de la rencontrer! La nature, pour commencer, peut lui offrir en cadeau des sections elliptiques quasi parfaites sur certains volcans, nous allons expliquer pourquoi. Il est moralement impossible de commencer ailleurs que près de Clermont-Ferrand, avec une pensée pour Blaise Pascal, auteur à 16 ans d'un Essai pour les Coniques, hélas perdu. La forme, très caractéristique, du Puy de Dôme évoque une section plane, et la vision de haut des cratères d'autres volcans de la chaîne des Puys suggère plus souvent une ellipse dans un plan légèrement incliné qu'un cercle, qu'elle serait si le plan de section était horizontal, perpendiculaire à l'axe du cône de révolution qui est, en première approximation, la forme du volcan.

Le Puy de Dôme,et  d'autres Puys tout près, que le randonneur peut voir d'en haut...
Pourquoi? L'expérience montre qu'un tas de sable réalisé par écoulement vertical à partir d'un point unique, sur le plan horizontal, est un cône de révolution qui a toujours le même demi-angle au sommet. Cela résulte des propriétés mécaniques du sable, de son comportement lors des écoulements, de fait la pente est d'environ 30°. Si l'on perce la plaque support, on crée un deuxième cône, "en creux", cette fois, mais même demi-angle au sommet. Suivant la position du trou (aligné verticalement avec le sommet du tas ou non), on obtient un cercle ou une ellipse... Si on veut le démontrer rigoureusement, ce n'est pas très difficile, à condition de savoir qu'un cône a une équation du type z²  = k. ( x² + y² ) dans un repère bien choisi; ce qui est très important, c'est que k est le même pour les deux cônes, car il ne dépend que de la pente.

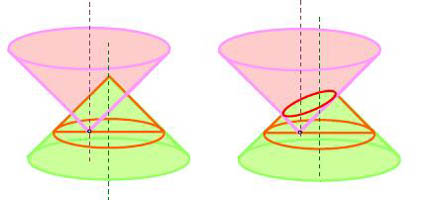
Images extraites d'un remarquable travail de lycéens : "La Géométrie du Tas de Sable", réalisé dans le cadre des ateliers "Maths en Jeans"
Sur un volcan, les chose se passent de même, s'il s'est constitué par accumulation de cendres, notamment. Qu'après un repos une nouvelle cheminée se perce... pas exactement sur le trajet de la première, et le tourr est joué: un effondrement des cendres conique se produit, et on obtient notre ellipse! La perfection initiale s'altère avec l'érosion, parfois inégale, mais on en garde une assez bonne impression, même sur un exemple de bien plus grande taille que les précédents!


Le cratère de Vulcano (Iles Éoliennes, Italie).
Vous pouvez faire la promenade tout autour pour bien sentir que la courbe est dans un plan incliné; la deuxième photo est prise depuis le point le plus haut.

Que manque-t-il pour mieux voir le phénomène? Sans doute un peu de hauteur! Voici donc un moyen très agréable d'admirer la définition d'Apollonius: monter à bord d'une montgolfière! Et, si cela ne permet pas de dominer un volcan, pourquoi ne pas regarder l'ombre portée sur le plan du sol de la demi-sphère constituant la partie supérieure du ballon ? (négligeons l'effet de "tranches" produit par les cordages...) Le soleil matinal allonge les ombres, le cône d'ombre (qui est le cône circinscrit à la sphère) coupe nettement le plan suivant une ellipse!

Soleil matinal sur les montgolfières en Cappadoce (Turquie).
À gauche, l'ombre de la demi-sphère supérieure vient précisément  d'atteindre le plan horizontal du plateau.

On trouvera la section parabolique sur des cadrans solaires hellénistiques, donc contemporains de notre héros (voir les détails géométriques sur notre page consacrée au cadran d'Eudoxe) 

Le "cadran d'Eudoxe", à Cnide: un cône dont la section horizontale est parabolique.

enfin l'hyperbole apparait à foison grâce à des modèles un peu plus tardifs, cadrans verticaux ou horizontaux: le mouvement apparent du soleil étant un cercle, l'extrémité du style un point fixe jouant le rôle de sommet pour le cône des rayons, sa trace dans le plan du cadran est, pour un jour donné, une branche d'hyperbole dénommée arc diurne : c'est exactement la définition du Livre I qu'on applique alors!  Ses les positions extrêmes, obtenues aux deux solstices sont toujours figurées sur le cadran; parfois s'y ajoutent les arcs de quelques dates d'entrée du soleil dans un signe du zodiaque.

Hyperboles "extrêmes" sur un cadran vertical (Institut de France, Paris), horizontal (Gavarnie, Hautes Pyrénées)

Avec plusieurs hyperboles intermédiaires, correspondant à d'autres entrées du Zodiaque. (Görlitz, Allemagne)

Un cas d'exception apparaît -qu'Apollonius n'a pas oublié dans son traité: si le sommet est dans le plan de section, cette trace sera une portion de droite; c'est ce qui arrive lors des équinoxes de printemps et d'automne.


Cadran solaire de la Sorbonne (Paris)
Journée du Patrimoine, un 21/09... soit, à très peu près, à l'équinoxe !

De la définition d'Apollonius, les mathématiciens Iraniens du X ème siècle Al-Quhi, puis Al-Sijzi ont dérivé le principe d'un instrument capable de tracer -en théorie du moins!- toutes les coniques, et que l'on a appelé pour cette raison compas pafait.

une réalisation moderne du compas parfait
Quand le bras supérieur, à angle droit de l'axe, décrit un cercle, le point S reste fixe; à l'extrémité de la tige figurant la génératrice, une pointe feutre coulisse librement dans le tube, restant toujours au contact du plan (P); en fonction de l'inclinaison réglable de celui-ci, la pointe trace la conique section selon la définition d'Apollonius.
[ Plus de précisions et une animation sur cette page du "Theatrum Machinarum" du Musée de Modène. ]

Remarque touristique: Jusqu'ici, nous n'avons évoqué que des cas où c'est la définition d'Apollonius qui se donnait en spectacle, mais il y a de nombreuse autres occasionsde voir des coniques. Ainsi, la parabole est très fréquente, au service cette fois d'une propriété mécanique: il suffit d'observer le câble supérieur d'un pont suspendu. (Attention, ce n'esgt PAS un arc de chaînette, qui est la forme prise par un fil pesant sous l'action de son seul poids -ce qui n'est clairement pas le cas du pont, dans lequel elle est négligeable devant celui du tablier.)


Pont suspendu à Wroclaw (Pologne)

L'ellipse a servi de modèle de base pour les amphithéâtres dés l'antiquité Romaine, avant d'inspirer Bernini à la Renaissance pour la place Saint-Pierre, ou Charles L'Enfant à Washington pour The Ellipse. (beaucoup de détails historico-mathématiques en suivant ce lien.)

Amphithéâtre Romain à El-Jem (Tunisie) The Ellipse à Washington; photo provenant du site... [cliquez sur l'image!]

Mais... s'agit-il vraiment d'ellipses, ou... d'approximations? Pour en savoir plus sur cette question, plus délicate qu'on ne croirait au premier abord, rendez-vous sur notre page relative aux cylindres où vous trouverez la position du problème et des liens.

Revenons donc pour conclure à l'ellipse parfaite: vous avez sûrement regretté de ne pas la  trouver ci-dessus sur un cadran solaire. Mais c'est possible: il suffit pour cela de changer... de type de cadran! Passons au cadran analemnatique, souvent dénommé, en France, cadran de Brou (voir aussi cette page), en raison du plus célèbre et plus ancien connu du genre, celui de l'église du XVI ème siècle d'un petit village de l'Ain. Par un bienheureux hasard, c'est à Bourg-en-Bresse que naquit celui qui devint un astronome réputé et le restaura à ses frais en 1757, Jérôme de Lalande (1732-1807 ). Il en publia deux études mathématiques, en 1757 et 1783. Ce n'est pas ici l'objet de le décrire entièrement ; précisons seulement ceci pour notre propos:
tout cadran est une projection du cadran équatorial, circulaire et divisé en tranches égales de 15°. (la base circulaire du cône de révolution, qu'on coupe par des plans horizontaux et verticaux différents, comme on l'a vu précédemment.)  Au lieu d'employer une  projection conique, revenons à la projection cylindrique. Le cercle dans un plan incliné se projette suivant une ellipse: autrement dit, cela se passe comme pour la sectionde colonne vue à Pergé en début de page, mais cette fois, le cercle est dans le plan incliné, et l'ellipse dans le plan horizontal. Les divisions horaires régulières sur le cercle se projettent aux points de l'ellipse matérialisés par les plots métalliques (techniquement, un rabattement du cercle sur le plan horizontal permet de construire aisément ces points par l'affinité qui envoie le cercle sur l'ellipse). Une particularité de ce cadran est que le gnomon dont la projection indiquera l'heure est... l'observateur lui-même, qui devra se placer en un point, variable selon la date, de la projection du méridien, c'est pourquoi celui-ci est gradué.
Était-il un meilleur lieu que celui qui vit Apollonius écrire son traité pour observer cette nouvelle application de sa définition des coniques?

Alexandrie (Egypte), parvis de la Nouvelle Bibliothèque Portrait de Jérôme Lalande,
Obsevatoire de Paris

Aujourd'hui, n'importe quel touriste, en prenant une photograhie d'un cercle sous un angle différent de 90°, applique sans le savoir la définition d'Apollonius: le résultat vu sera une ellipse! Voici un exemple qui devrait parler... à votre imagination.

New York (U.S.A.), au cœur de Central Park : in Memoriam John Lennon...

Remarques sur le style, l'esprit, la méthode du Traité

On l'a déjà dit: le style est celui d'Euclide, qui n'a pas fini de marquer des générations de mathématiciens! Définitions et propositions s'enchaînent impeccablement, et, si les démonstrations sont sans reproches, jamais il ne dit un mot sur ce qui l'a guidé dans la découverte.

Mais Apollonius n'est pas qu'un suiveur d'Euclide, il est aussi un précurseur de Descartes: sa présentation équivaut souvent à l'emploi de coordonnées cartésiennes obliques! Pas de  ( x , y ), certes, mais, dit en longueurs de segments bien choisis, cela revient strictement au même, et permet une transcription moderne relativement aisée . Par exemple, dans la proposition 1 sur la section parabolique, l'équation, au lieu d'être notée
y² = 2px
s'écrira, avec les longueurs de segments repérés sur la figure (voir ci-dessus les notations) et sous forme d'égalité des aires d'un carré et d'un rectangle
QV² =PL.PV
Un simple coup d'oeil suffit pour contrôler que PV est l'abacisse, QV l'ordonnée, PL étant une longueur fiixe.

Enfin, son approche visionnaire s'exprime lorsqu'il défend l'étude des mathématiques pour elles-mêmes en se dégageant d'une utilité immédiate:
"D'ailleurs, indépendamment d'une telle utilité, les démonstations sont dignes d'être admises pour elles-mêmes, car nous admettons de même beaucoup d'autres propositions dans les mathématiques pour elles-mêmes et non pour d'autres raisons."
Préface au Livre IV
La récompense de cette sagesse sera éclatante, lorsqu'en 1609, Kepler découvrira enfin, après huit ans de labeur acharné sur la tajectoire de Mars et des calculs, dit-il, recommencés 70 fois, que l'orbite des planètes est... une ellipse, ce que démontrera Newton en 1687 à partir de sa loi de gravitation universelle.


Les héros ultérieurs de l'ellipse ( site philatélique de Jeff Miller )

Pourquoi faire simple quand on peut faire compliqué? (Pr. Schadocko) 

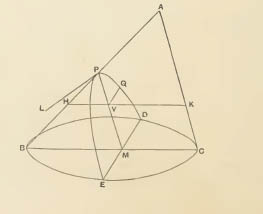
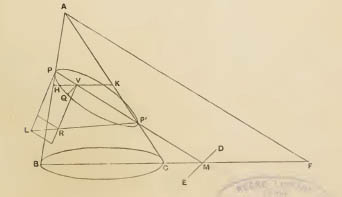
La suite du Livre I donne la définition classique des diamètres: sur la figure ci-dessous, les cordes parallèles à QQ' (ex: BB') ont leur milieu sur une droite, le diamètre  PP'. Et la tangente en P est ensuite définie comme... parallèle à  QQ' passant par P, autrement dit: "corde qui coupe en deux points confondus en un seul"!

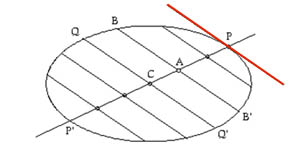En rouge, définition de la tangente selon Apollonius
Il n'y a rien à redire... sinon que c'est bien compliqué! Bien sûr, objecterez vous, quand le calcul infinitésimal n'a pas encore été inventé, rien de tel n'est simple... Mais Apollonius aurait pu utiliser sa merveilleuse définition, en disant:
1) je sais définir la tangente à un cercle (perpendiculaire au rayon);
2) utilisons le cône: elle se projette coniquement en la tangente à l'ellipse, hyperbole ou parabole section (selon l'inclinaison de son plan).
Les choses simples n'ont qu'un défaut: il est difficile de les découvrir, si évidentes puissent-elles paraître après coup. Une fois utilisé l'espace pour définir les coniques, Apollonius ne s'en est plus servi... et ce point de vue attendra pas mal d'années pour que son intérêt soit perçu:  Desargues et Pascal au XVII ème siècle seront les pionniers, et l'idée trouvera sa consécration au XIX ème siècle seulement avec Poncelet et son Traité des Propriétés Projectives des Coniques.

Les autres Livres fondamentaux ( II à IV )

Rendons la parole à l'auteur pour présenter, toujours dans l'adresse à Eudème qui ouvre le Livre I, la suite de son travail. Ses commentateurs (notamment Pappus qui le juge arrogant envers Euclide dont il critique le caractère partiel de certaines solutions) lui reprocheront parfois de manquer de modestie, mais il était fier de ses apports et conscient de leur réel intérêt :

"Le second livre traite des diamètres, des axes et des asymptotes  [...] ; le troisième livre contient beaucoup et d'admirables théorèmes [...] , la plupart sont beaux et nouveaux. [...] Le quatrième livre apprend de combien de manières les coniques peuvent se rencontrer entre elles et avec la circonférence, et beaucoup de propositions appartenant à une théorie complète, ce qui n'a jamais été publié par aucun de nos devanciers."
Entre autres merveilles, le Livre III -dont la préface propre est hélas perdue- contient tous les théorèmes usuels relatifs aux foyers; citons seulement
 -  la définition bifocale de l'ellipse, lieu des points M  tels que MF + MF' = 2a, qui permet le "tracé du jardinier";
 -  celle, similaire, de l'hyperbole: lieu des points M  tels que MF - MF' = 2a ou MF' - MF = 2a, qui permet...  une construction similaire (mais un peu moins connue)
 -  la propriété de réflexion des rayons lumineux ou sonores d'un foyer vers l'autre.
Construction bifocale de l'hyperbole avec un traceur en fils tendus:
 réalisation moderne du "Theatrum Machinarum" du Musée de Modène.		 En 1636, dans l'Harmonie Universelle, Mersenne connait la propriété de réflexion et l'applique à l'écho.

Curieusement, le cas de la parabole, connu de son prédécesseur Archimède (ses célèbres miroirs ardents) est passé sous silence;  la génération par  foyer et directrice n'est pas non plus mentionnée.

La Chaise-Dieu : quand la géométrie... préserve le secret de la confession
Même s'il y a loin de Pergé au fin fond de la Haute-Loire, il est possible d'expérimenter cette propriété avec les ondes sonores, dans la célèbre -et bien nommée- Salle de l'Écho de l'abbaye de La Chaise Dieu. L'endroit est désomais mondialement connu grâce au festival de musique qu'y fonda, en 1966, Georges Cziffra, tombé amoureux du lieu. La salle n'est ni dans l'église, ni dans le cloître; elle fait partie d'un ancien bâtiment conventuel, sur la gauche de l'église et bénéficie d'un accès séparé...place de l'écho.
l'église Saint-Robert Allure de l'ensemble; flèche sur l'entrée de la salle de l'Écho
(d'après un dépliant de l'Office de Tourisme)		 Entrée de la salle de l'Écho,
sur la place éponyme.

Le plafond est orné de deux lignes décorées, à la verticale des diagonales de la salle. Elles sont réputées être deux demi-ellipses; chacune d'elle permet de converser à voix basse d'un coin au coin opposé en diagonale, sans être entendu des autres personnes présentes dans la salle. Ce qui fonctionne très bien; en particulier, si les quatre coins sont occupés, chacune des deux conversations se déroule sans même soupçonner la présence d'une discussion selon l'autre plan diagonal. Ainsi, deux confessions pouvaient-elles être menées simultanément, tout en garantissant le secret de chacune vis à vis de l'autre comme vis à vis des personnes de passage dans la salle. On sait que l'abbaye comportait trois salle du même modèle; une seule a été conservée.
Vue générale: la salle et deux quarts d'ellipse "diagonaux"

On a autrefois avancé l'idée, aujourd'hui discutée, d'un ingénieux confessionnal pour les lépreux: ainsi, le prêtre aurait-il pu remplir son devoir de conscience... sans prendre le risque sanitaire d'approcher le pénitent. Une objection historique sérieuse est qu'à l'époque de la construction (XVIIème siècle), la lèpre était partout en régression, et ne menaçait pas particulièrement la région. D'un autre côté, pourquoi imaginer un dispositif si compliqué? Deux confessionnaux usuels prennent bien moins de place! 


On peut être légèrement surpris de la position des expérimentateurs amateurs, très près des sommets de l'ellipse. Toutefois, le fort applatissement du plafond (que montre l'image ci-dessus) donne, à l'estimation, une excentricité à coup sûr supérieure à 0.9, et probablement de l'ordre de 0.95. Ce qui siginifie que le foyer (point idéal de l'expérience) est distant du sommet de moins de 1/10ème de la demi-diagonale, soit moins d'un mètre. De plus, l'onde sonore émise n'est pas unidirectionnelle, ce qui laisse une petite latitude de placement...

Les voûtes forment deux cylindres elliptiques, dont l'intersection consiste en ces deux ellipses (Mieux le voir dans notre page: Intersection de Quadriques). Ce n'était en tout cas ni le plus facilele, ni le plus rapide à réaliser.
Simple plaisir de l'architecte, alors? La Salle de l'Écho garde encore quelques secrets par devers elle.


Le Livre IV est consacré à l'étude des intersections des coniques entre elles, ou, précise-t-il avec un cercle: c'est donc une discussion complète du nombre de points d'intersection des courbes du second degré, un sujet qui, à sa connaissance, n'a été traité de manière complète et satisfaisante par aucun de ses prédécesseurs. Il  en souligne l'intérêt pratique pour la résolution des problèmes menant à des équations du troisième degré (qu'on appellait alors problèmes solides), ceux pour lesquels Ménechme avait introduit ces courbes, et juste après l'intérêt théorique de l'étude du problème pour lui même: c'est dans ce contexte qu'apparaît la citation donnée plus haut.
Nul n'aura mieux compris la portée de ces vues qu'Omar Khayyam (1048-1131), dans ce qui est le tout premier ouvrage sur la résolution systématique des équations du troisième degré. Simplement intitulé Traité d'Algèbre et d'Al Muqabala, il classifie systématiquement les équations du troisième degré avant de résoudre chacun des cas géométriquement par l'intersection de deux coniques judicieusement choisies. Présentant son travail, il dit

"Il faut bien savoir que ce traité ne sera compris que de ceux qui maîtrisent le livre d'Euclide sur les Éléments et son livre sur les Données, ainsi que les deux [premiers] livres de l'ouvrage d d'Apollonius sur les Coniques. Celui à qui la connaissance d'un de ces trois livres fait défaut ne peut avoir accès à la compréhension de ce traité. Je me suis du reste appliqué, avec peine, à ne renvoyer dans ce traité qu'à ces trois livres."
"Ce qu'on peut démontrer par les propriétés du cercle, je veux dire par les deux ouvrages d'Euclide, les Éléments et  les Données, démontrons le en tâchant de le rendre facile. Et qu'on ne peut démontrer que par les sections coniques, démontrons le par les deux livres des Coniques. "
Le sens de ce deuxième extrait est le suivant: ce qui est du simple ressort d'une équation du second degré peut être résolu élémentairement, à l'aide d'intersections de cercles et de droites; tout l'outillage nécessaire à cette fin est dans Euclide. Ne recourons aux coniques que lorsqu'on y est impérieusement contraint... et en ce cas, notre référence sera Apollonius. À chaque usage, on le verra d'ailleurs mentionner les références précises des propositions employées.


Première page d'un manuscrit du Traité de la Division du Quart de Cercle, ouvrage antérieur -et préparatoire- au Traité d'Algèbre et d'Al Muqabala
Khayyam emploie l'intersection d'un cercle et d'une hyperbole; il cite, pour la seule analyse du problème (cette page) quatre propositions du Traité des Coniques d'Apollonius.

Les derniers Livres  ( V à VIII )

Le Livre V est, selon Terquem, l' "honneur de l'esprit humain, et le plus beau reste de la science antique" ; il traite des minima et maxima de la distance d'un point à une conique. Bien sûr, il les localise sur des normales à la courbe, dont il discute le nombre. Ce qui le conduit à la mise en évidence du centre de courbure et de la développée de celle-ci!
Suggérons l'idée, sous une forme simplifiée, sur la parabole -quoiqu'elle soit de nouveau absente du texte à ce point- parce que la figure est plus lisible. Sur une normale (N) à la parabole, il détermine un point J partagenat la perpendiculaire (D) abaissée sur  l'axe en deux portions, suivant le nombre de normales, 1 ou 3, que l'on peut mener à la courbe selon l'ordonnée sur  (D). Par cette propriété, il vient de mettre en évidence le centre de courbure J et son lieu quand (N) varie, qui est la développée de la conique. Heath, dans son édition d'Apollonius, montre que l'équation de la développée s'en déduit immédiatement dans le cas d'une ellipse; on obtient une astroïde allongée.

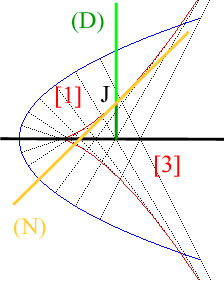
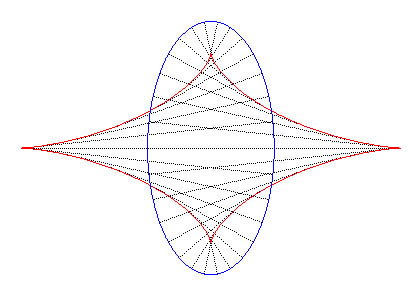Figures "supports" (traits fins noirs, bleus, rouges) issues de la page "Développée" du site MATHCURVE

Certains commentateurs plus récents (Fried & Ungaru) contestent quelque peu cette relecture, soutenant que Heath a beau jeu, connaissant les théories ultérieures, de les "projeter" rétroactivement dans le traité. Qu'il soit clair que la notion de courbure (par exemple, sous forme de recherche d'un cercle "optimal" parmi les cercles tangents à la conique et centrés sur la normale: Apollonius avait le moyen, sinon de résoudre, du moins de poser la question en ces termes) n'est jamais abordée par le savant grec, pas plus que celle d'enveloppe des normales: la développée est  pour lui une courbe séparatrice relative au nombre de normales issues d'un point. Sans avoir la prétention d'arbitrer ce débat, concluons que même si Heath "pousse" un peu, il n'a pas tort de remarquer que "tout est déjà là!"

Le Livre VI étudie l'égalaé et la similitude des coniques, tandis que le Livre VII revient sur les diamètres conjugués. L'auteur indique au Livre VI comment construire un cône (de révolution) dont une section elliptique est donnée.


Du Livre VIII, on ne connait que des tentatives de restitution.

Conclusion: peut-on encore s'intéressser à ces vieilleries?

Les Coniques n'ont rien perdu de leur attrait, ni de leur utilité... on pourrait même observer que l'Informatique et la Géométrie Algorithmique leur ont redonné un coup de jeunesse; dans nos liens, un cours élémentaire de Géométrie fait... par un spécialiste de ces domaines en témoignera. Et si l'on est parfois contraint à faire de tels cours "tardivement" dans les cursus, c'est parce qu'en dépit de leur importance on ne les enseigne plus assez au lycée...
Après la nécessité, le plaisir:  un des (LE?)  plus grands Physiciens du XX ème siècle, Richard Feynman, s'amuse à rebâtir, pour offrir un dernier cours moins scolaire à ses étudiants, les démonstrations géométriques de Newton pour établir le mouvement elliptique des planètes. C'est plus élémentaire (pas de calcul différentiel), ce qui, fait-il remarquer, ne siginifie pas plus facile. Mais il y prend un plaisir gourmand (même en rencontrant quelques obstacles...), alors... pourquoi pas nous?

Extraits choisis:

"Ce n'est pas difficile de démontrer que c'est une ellipse quand on sait manier les équations différentielles et les résoudre. [...] Normalement, on laisse au Département de Mathématiques le soin de prouver que c'est une ellipse, pour qu'ils aient quelque chose à faire là-bas avec leurs équations différentielles." [Rires]
"En revanche, au début de notre science -c'est à dire à l'époque de Newton- la méthode d'analyse géométrique, dans la tradition historique d'Euclide, était vraiment la seule façon de faire les choses. Et d'ailleurs, les Principia de Newton sont écrits de façon presque entièrement géométrique -tout ce qui est calcul différentiel était fait à partir de diagrammes géométriques. "
"Je veux vous faire conduire une buggy, pour son élégance, plutôt qu'une voiture sophistiquée.  [...] C'est bien plus facile à faire avec du calcul différentiel, mais vous allez le faire comme ça quand même, et vous devez vous rappeler que c'est pour la beauté du geste. "
"Le reste de la démonstration ne vient pas de Newton parce que je n'arrivais pas à très bien la suivre moi-même, parce qu'elle fait appel à trop de propriétés des coniques. J'en ai donc concocté une autre. "

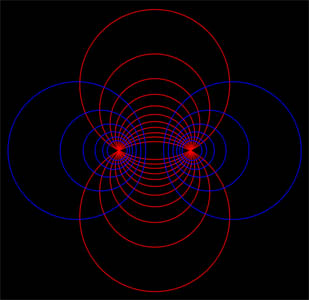
Feynman (couverture de l'édition Américaine et de la première édition Française) et les Principia de Newton;
entre les deux, un des diagrammes manuscrits provenant de ses notes de cours, reproduit dans le livre (voir réf.)

Les Cercles d'Apollonius

Apollonius est également célèbre pour avoir découvert que le lieu des points M tels que MA / MB = k est un cercle; quand k varie pour A et B fixés, ces cercles forment une famille, appelée faisceau à points limites ( A est obtenu pour k =0, B est obtenu pour k infini ). On les nomme cercles d'Apollonius; chaque cercle de la famille est orthogonal à chaque cercle de la famille des cercles passant par A et B . On peut en voir sur toutes les astrolabes: ce sont les cercles d'égale hauteur sur l'horizon, ou almucantarats. La famille orthogonale est celle des arcs d'égal azimut;  l'orthogonalité de ces familles sur la sphère céleste est conservée par le caractère conforme (conservation des angles) de la projection stéréographique, qui envoie la sphère sur le plan de l'équateur (visualiser dans l'espace).


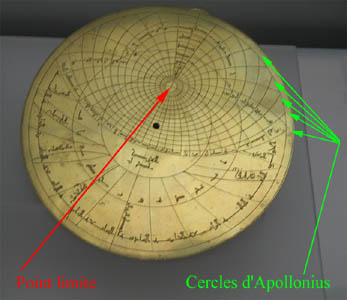Astrolabe andalouse, XIV ème siècle

Lorsque cadrans solaires et astrolabes verront leur gloire se faner, les cercles d'Apollonius ne disparaîtront pas, demeurant bien en évidence sur... les cadrans des horloges astronomiques. Celles de Prague et Strasbourg sont justement célèbres, en voici une autre, remarquable, mais moins connue, où nous retrouverons, à l'évidence, le même type de tympan:

Cathédrale de Saint-Omer (Pas de Calais); au dessus de la porte qui vit entrer... le Roi-Soleil !
On retrouve bien les deux familles de cercles orthogonaux précédents, almucantarats et cercles d'égale hauteur.
Le point limite visible est le zénith du lieu, l'horizon est le cercle délimitant la partie blanche (visible) de la noire (invisible).

Terminons sur une badinerie: bien sûr, le modèle théorique de ces cerclages en bois entassés est un faisceuau de cercles tangents... mais, en raison de l'épaisseur des lattes, convenez qu'on jurerait avoir découvert dans ce souk des faisceaux de cercles d'Apollonius!

Surprise au bazar égyptien d'Istanbul...

Bibliographie et Liens

En ligne

Livres

Si un lien est indiqué, des extraits peuvent être consultés sur Internet.
Revenir à la Home Page du Mathouriste