Non décomposée (lucarne à gauche de l'image)       Décomposée (chapeau de cheminée)    
             

Attention, ce ne serait pas la célèbre fenêtre de Viviani, car elle n'est pas sphérique... Sa projection horizontale serait certes une lemniscate (courbe en forme de 8), mais du modèle
Ajoutons qu'un seul nœud ne fait pas la décomposition: il en faudrait deux, et cela n'arrive que si les deux cylindres sont de même rayon. Cette chose rare architecturalement, plus encore que la décomposition, le Mathouriste pense l'avoir trouvée dans les vomitoires du théâtre de Milet: la courbe est nodale (on n'en voit qu'une portion -à droite-, puisque le cylindre défini par la voute de l'escalier ne se prolonge pas au dela de l'intersection), et pour autant qu'il se souvienne, les cylindres n'étaient pas isométriques!

Lorsque le matériau est la pierre, le travail exige une grande expertise dans la coupe: en témoignera l'Observatoire de Paris, de l'architecte Claude Perrault.

Intersections de Cylindres: Génératrices Horizontales et Verticales 

Le Mathouriste a eu l'heureuse surprise de découvrir un exemple plus ancien à Ostie, le port de la Rome antique. L'emploi de la brique a permis un travail précis sur la courbe d'intersection -qu'on en juge par les détails ci-dessous- sans faire appel à une expertise  sur les coupes de pierre qui, pas mal d'années après (voir plus haut nos images de l'Observatoire de Paris), mobilisera des géomètres aussi fameux que Desargues et Monge... Ce bâtiment date probablement du II^ème ou III^ème siècle de notre ère.

Avec des Cylindres Elliptiques...

La Salle de l'Écho, à l'abbaye de La Chaise-Dieu, a pour plafond une voute formée de deux portions de cylindres elliptiques, d'axes perpendiculaires. Ils ont été construits pour que leur intersection soit décomposée en la réunion de deux ellipses, dans les plans verticaux ayant pour bases les diagonales de cette salle rectangulaire: c'est ce qui permet d'exploiter la propriété bifocale de l'ellipse pour garantir le secret des conversation. (voir cet encadré de notre page Apollonius à Pergé). Le caractère cylindrique est évident au premier regard: les maçons ont manifestement travaillé avec des règles, et c'est naturel. Dès lors; chacune des surfaces est un cylindre, et, les génératrices s'appuyant sur une des deux ellipses de l'intersection voulue,les deux cylindres sont elliptiques.
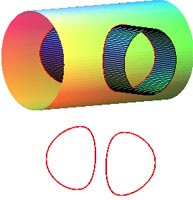
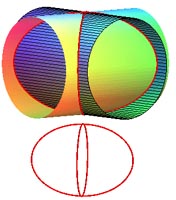
Nous en avons aidé la visulisataion sur l'image de droite, en coloriant en rouge les génératrices de l'un, en bleu celles de l'autre :

vue latérale	vue de face	illustration des génératrices des deux cylindres

Les génératrices rouges, quasi frontales, conservent leur parallélisme dans l'image, tandis que les bleues, elles-aussi parallèles entre elles, par effet de perspective de la photo, convergent vers un point de fuite approximativement situé en bas et à droite (sur le montant droit de la fenêtre).
Ces deux cylindres ont une une intersection décomposée en les deux ellipses dont le tracé est matérialisé par les décorations du plafond; ce sont elles dont on utilise la propriété de réflexion d'un foyer à l'autre pour transmettre deux conversations à voix basse (confessions), inaudibles des autres points de la salle. Il s'agit donc dans ce cas d'une propriété des courbes, et non des surfaces (cylindres elliptiques, ou ellipsoïdes).

Quand le Soleil décompose les Intersections...

Cône et Sphère

Supposons qu'un cône et une sphère aient un cercle en commun. L'application du théorème initialement rappelé fait qu'ils auront une deuxième conique en commun. Et comme celle-ci est une section plane de la sphère... ce sera un deuxième cercle!
La figure est banale si le cône est de révolution, et la sphère centrée sur son axe: les deux cercles sont parallèles. Elle l'est beaucoup moins lorsque le cône est quelconque et oblique! Or, il existe un endroit où l'on peut admirer ce cas, et où il résulte de la volonté architecturale. Beaucoup de gens le voient chaque année, ... mais bien peu en voient la géométrie: c'est le Panthéon de Rome. Son ouverture sommitale circulaire définit, avec le soleil pour sommet, un cône de lumière... qui recoupe la coupole sphérique suivant un autre cercle, quelle que soit l'heure (et l'inclinaison du soleil, qui correspond à un déplacement apparent du sommet du cône). Il faudra bien sûr, pour cela, faire abstraction des caissons décoratifs.


" J’avais voulu que ce sanctuaire de tous les Dieux reproduisît la forme du globe terrestre et de la sphère stellaire, du globe où se renferment toutes les semences du feu éternel, de la sphère creuse qui contient tout. [...] Ce temple ouvert et secret était conçu comme un cadran solaire. Les heures tournaient en rond sur ces caissons soigneusement polis par les artisans grecs ; le disque du jour y resterait suspendu comme un bouclier d’or. "
Ainsi peut-on écrire un roman à succès, gagner une place à l'Académie Française, et n'avoir pas vu l'essentiel... pour un mathématicien.

Cône et Cylindre

Un grand bon dans le temps va nous mener à un temple... de l'art contemporain, le Hirshhorn Museum de Washington (USA), œuvre de l'architecte Américian Gordon Bunshaft (1974). Extérieurement, le musée apparait comme un cylindre sans ouverture...
... mais c'est en fait un double cylindre, les espaces d'exposition se trouvant entre les deux cylindres coaxiaux. Le visiteur féru d'Art et de Géométrie y fera d'ailleurs d'intéressantes rencontres, et le Mathouriste compte bien vous en reparler prochainement, et tout particulièrement d'Hnery Moore.
Pour l'instant, contentons nous de pénétrer dans sa cour centrale, où un jet d'eau matérialise l'axe des cylindres concentriques.
Au soleil du soir -ou du matin (il faut, pour apprécier au mieux, une certaine inclinaison des rayons du soleil), le cône de lumière coupe le cylindre intérieur selon son cercle sommital, et le recoupe donc suivant une deuxième conique -une ellipse, cette fois, puisque c'est une section oblique du cylindre. Voici le résultat!


Le grand diamètre de l'ouverture interdit de voir l'ellipse dans sa totalité -il faudrait pour cela que le bâtiment soit beaucoup plus haut.  La portion  tracée permet de bien se rendre compte de sa nature, y compris d'en apprécier la planéité, en se positionnant sur son axe projeté, et en jetant alternativement son regard à droite et à gauche.

Remarque:

L'ensemble des rayons solaires frappant le cercle sommital peut aussi être considéré comme un cylindre (rayons parallèles: le cylindre n'est qu'un cône dont le sommet est rejeté à l'infini.)
Cela ne change rien aux résultats énoncés: l'intersection est décomposée (deux quadriques ayant une conique commune), et l'intersection reste une ellipse au Hirshhorn, un cercle au Panthéon, parce qu'il reste section plane de la sphère!

Vers les autres sections: