Vincenzo VIVIANI
et sa célèbre fenêtre
Comme le
célèbre sextuor de Tchaïkovski, cela
pourrait s'intituler Souvenir
de Florence, puisque ce mathématicien y passa
toute sa vie (1622-1703). Vous la trouverez
présentée ici ou là, mais pourquoi ne
pas la savourer dans un style "d'époque", avec l'Éloge
de Monsieur Viviani que Fontenelle,
Secrétaire Perpétuel, présenta
à
l'Académie des Sciences pour lui rendre un hommage posthume.
C'est donc dans divers lieux de cette ville que nous vous invitons à découvrir les traces de sa présence. Quant à sa célèbre courbe... c'est, comme on le découvrira, ailleurs qu'il conviendra de la chercher!
Viviani a donc 17 ans quand il devient secrétaire et disciple de Galilée; et il le restera 3 ans, jusqu'à la mort de son mentor. Après quoi, il veillera à ses funérailles et à la conservation de sa mémoire... Dès lors, c'est en se livrant à un "Parcours Galilée" dans la ville (encore de bien belles promenades: il faudra que le Mathouriste prenne le temps de vous les faire partager...) qu'on rencontrera Viviani.

Tito Lessi, Galileo & Viviani, 1892 (Musée Galileo, Florence)
Cette demeure fut conçue par l'architecte Giovan Battista Nelli au XVème siècle, ornée d'un buste de Galilée en 1610, œuvre deGiovanni Caccini ; Viviani y fit installer les panneaux gravés en 1693. Elle st aujourd'hui occupée par SACI Studio Art Centers International, organisation Américaine à but non lucratif pour l'enseignement artistique.

Élévation de la façade, XVIIIème siècle (source: page Wikipedia Italienne).
Voici ce qu'en dit Fontenelle:
Quelques remarques s'imposent:
On peut imager l'opération de manière très simple: et très parlante pour le non-mathématicien: c'est le résultat de l'action d'un dénoyauteur à cerises (indispensable à la réalisation d'un bon clafoutis), (S1) sur la figure ci-dessus, dont la perforation n'est pas centrée sur un axe de la sphère (S2), mais la frôle tangentiellement...
On donne souvent la description équivalente: lieu
des
points dont la longitude est égale à
la latitude. Un bateau qui naviguerait dans l'Océan
Pacifique (choisi pour qu'il y ait la place...) en suivant toujours
cette règle décrirait une fenêtre de
Viviani. C'est d'ailleurs la manière choisie par Jakob
Bernoulli pour la décrire, en la donnant comme solution du
problème; mais ni lui, ni Viviani n'explicitent leur calcul
d'aire; ils se contentent d'affirmer le résultat.
Pour les amateurs d'équations, précisons ces deux formes, en coordonnées cartésiennes d'origine O, centre de la sphère, puis en coordonnées sphériques: θ, φ désignant respectivement longitude et latitude, il suffit de faire θ = φ dans la représentation de la sphère en coordonnées sphériques.
Une combinaison évidente (retrancher à la première deux fois la seconde) permet de définir la courbe comme intersection du cylindre et d'un cône, reconnu comme promis à l'homogénéité de l'équation
Reste à en voir l'intérêt. C'est une technique inventée par Monge, dans sa Géométrie Descriptive, pour trouver les tangentes à l'intersection de deux surfaces en un point où elles ont même plan tangent. Clairement, en ce cas, le théorème : " La tangente en M à la courbe d'intersection de deux surfaces est l'intersection de leurs plans tangents respectifs en M" ne s'applique plus; c'est ici le cas en S.
Monge a alors l'idée de prouver que "la tangente au sommet du cône à un arc tracé sur celui-ci est encore une génératrice du cône". C'est facile analytiquement, mais un argument "d'époque" -si l'on ose dire- est le suivant: pour tout point P de la courbe voisin de S, la sécante SP est une génératrice; sa limite, qui est la tangente en S, en est encore une.
Dès lors, la tangente à tout arc passant par S est située:
1) sur le cône de sommet S et directrice la courbe de Viviani (nous venons d'en obtenir l'équation par manipulation élémentaire);
2) dans le plan tangent en S au cylindre (commun avec la sphère).
Les tangentes sont donc les génératrices d'intersection du cône avec ce plan, ce qui en fournit la construction sans aucun calcul!
Néanmoins, trouver dans un monument une intersection sphère-cylindre exactement positionnée reste un défi intéressant, que le Mathouriste n'a pas encore été capable de relever. Examinons de plus près les contraintes:

Paris, Grand Palais. Deux cylindres, une sphère, une rencontre... mais pas celle que l'on souhaite!
En effet, si l'on observe la structure tubulaire (photo de droite), on constate qu'à chaque point où ces lignes rencontrent les méridiens, l'angle est manifestement de 45°. .
Les côtés des quadrilatères curvilignes forment une version discrétisée d'une courbe qui vérifierait cela en tout point; naturellement seul l'éloignement crée l'illusion visuelle d'une courbe lisse! Les architectes qui cherchent un tel effet ne s'en cachent pas (voir par exemple [5]); c'est la longue tradition qui part du calcul de π par Archimède et aboutit à l'illusion de voir des courbes lisses sur nos écrans d'ordinateur (et plus l'acran comporte de pixels, meilleure elle est) en passant par la définition du ds² selon Leibniz, qui applique à un triangle curviligne infinitésimal le théorème de Pythagore pour un triangle ordinaire.
Le modèle à chercher est donc une courbe dont le vecteur unitaire tangent en tout point ferait lun angle de 45° avec les méridiens (ou les parallèles); un calcul en coordonnées sphériques fournit.
Ces courbes ne sont pas algébriques (en raison de la présence du ln, notamment) et ne s'obtiennent donc pas par intersection de surfaces du second degré; ce qui interdit qu'il s'agisse de courbes de Viviani.
"VINCENZIO VIVIANI, Gentilhomme
Florentin, naquit à Florence le 5 Avril 1622.
À l'âge de 16 ans, son Maître de
Logique, qui
étoit un Religieux, lui dit qu'il n'y avoit point de
meilleure
Logique que la Géométrie, & comme les
Géomètres qui encore aujourd'hui ne sont pas fort
communs, l'étoient beaucoup moins en ce tems-là,
il n'y
avait alors dans la Toscane qu'un seul Maître de
Mathématique, qui étoit encore un Religieux, sous
lequel
M. Viviani commença à étudier."
C'est donc dans divers lieux de cette ville que nous vous invitons à découvrir les traces de sa présence. Quant à sa célèbre courbe... c'est, comme on le découvrira, ailleurs qu'il conviendra de la chercher!
  |
|
 |
|
| Portrait par Pietro Stoppioni,1806 (Musée Galilée, Florence) | |
| Médaillon à La Specola (Museum d'Histoire Natrurelle, Florence) | |
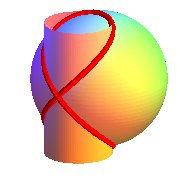
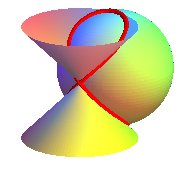
| Fenêtre de Viviani, diverses intersections (site Mathcurve.com de Robert Ferréol) | |
Les Lieux
Rien n'explique mieux où le rencontrer que de poursuivre la lecture de l'Éloge de Fontenelle:"Le
grand Galilée étoit alors fort
âgé, & il
avoit perdu, selon sa propre expression, ces yeux qui avoient
découvert un nouveau Ciel. Il n'avoit pas cependant
abandonné l'étude; ni son goût, ni ses
étonnants succès ne lui permettaient de
l'abandonner. Il
lui falloit auprès de lui quelques jeunes gens, qui lui
tinssent
lieu de ses yeux, & et qu'il eût le plaisir de
former. M
Viviani à peine avoit
étudié la Géométrie un an,
qu'il fut digne
que Galilée le prît chez lui, & et en
quelque
manière l'adoptât. Ce fut en 1639."
Viviani a donc 17 ans quand il devient secrétaire et disciple de Galilée; et il le restera 3 ans, jusqu'à la mort de son mentor. Après quoi, il veillera à ses funérailles et à la conservation de sa mémoire... Dès lors, c'est en se livrant à un "Parcours Galilée" dans la ville (encore de bien belles promenades: il faudra que le Mathouriste prenne le temps de vous les faire partager...) qu'on rencontrera Viviani.
Deux (ou trois) Musées...
D'abord, le nouveau -et splendide- Musée Galilée (il s'appelait Museo di Storia della Scienza avant 2010) abrite, outre le portrait ci-dessus, un tableau représentant Galilée en compagnie de Viviani. On reconnait mieux le premier que le second, mais puisque c'est le site Internet du musée qui le dit....Tito Lessi, Galileo & Viviani, 1892 (Musée Galileo, Florence)
Sur l'autre rive de
l'Arno -l'Oltrarno comme
on l'appelle là-bas, le Museo di Storia Naturelle La Specola,
installé dans le palais Torrigiani sur la Via Romana, non
loin
du très connu Palais Pizzi, possède une salle
remarquable
dénommée Tribune
de Galilée (Tribuna di Galileo)
décorée de sculptures et peintures à
la gloire de
Galilée et ses disciples. Il s'agit d'un ensemble
pensé
de façon globale, homogène, voulu par Leopold II, Grand Duc de Toscane,
installé en 1841 dans ce lieu (qui était un
musée depuis
1771, destiné à abriter les collections
d'instruments de
physique et d'espèces naturelles accumulées par
les
Médicis); l'inauguration eut lieu à
l'occasion du
troisième Congrès des Sciences Italiennes.
Viviani, par Domenico
Tempesti (1690)
| |
|
| Buste de Viviani |
Galilée et ses deux plus célèbres disciples: Toricelli et Viviani |
| Tribune de Galilée (Musée La Specola, Florence) | |
Le buste de Viviani
est du sculpteur Luigi Magi; la statue de Galilée de
Aristodemo Costoli, à qui l'on doit aussi celle de laTribune
des Offices.
Le portrait le plus fréquemment montré (pages Wikipedia) est présenté à la Galerie des Offices; il a l'avantage d'avoir été peint de son vivant..
Le portrait le plus fréquemment montré (pages Wikipedia) est présenté à la Galerie des Offices; il a l'avantage d'avoir été peint de son vivant..
...et un Palais!
Viviani habitait
près de l'église Santa Maria Novella (et donc,
aujourd'hui, près de la gare centrale) le Palazzo dei
Cartelloni, parfois désigné en
Français comme Palais
des Placards. Il avait fait décorer la
façade de sculptures représentant des affiches
(les placards),
sur lesquelles est écrit en Latin un texte à
la
gloire de son maître, dont un buste orne le portail. La rue
Sant'Antonino est particulièrement étroite, on
regrette
donc le manque de recul pour admirer cette façade, l'une des
plus originale de Florence!
| |
La rue Sant'Antonino et l'entrée du Palais. |
| |
||
| |
Détail : buste de Galilée au dessus du porche | Le "placard" de droite |
Cette demeure fut conçue par l'architecte Giovan Battista Nelli au XVème siècle, ornée d'un buste de Galilée en 1610, œuvre deGiovanni Caccini ; Viviani y fit installer les panneaux gravés en 1693. Elle st aujourd'hui occupée par SACI Studio Art Centers International, organisation Américaine à but non lucratif pour l'enseignement artistique.
Élévation de la façade, XVIIIème siècle (source: page Wikipedia Italienne).
Vincenzo
était d'une famille bien implantée à
Florence, depuis le 12ème siècle au moins; les armes de la famille sont visibles
près du Palais Strozzi.
La Fenêtre dans le Dôme
Un Curieux Problème...
C'est avec une certaine facétie -au point d'user d'un pseudonyme- que Viviani pose, en 1692, le problème dit de la Voûte quarrable, dont la célèbre courbe sera solution: il s'agirait de pratiquer des ouvertures dans un dôme hémisphérique, de façon à laisser subsister une portion de sphère quarrable : par là, il faut entendre que son aire s'exprime algébriquement en fonction de son rayon. (Rappelons qu'en l'absence d'ouverture, l'aire d'une hémisphère de rayon R s'exprime par 2πR2 et fournit un exemple "non quarrable" au sens donné par Viviani, quoique l'irrationnalité de π ne soit pas encore prouvée! )Une traduction (avec
quelques coquilles sur le nom de l'auteur)
Voici ce qu'en dit Fontenelle:
"Ce
problème de la Voute quarrable faisoit partie d'un Ouvrage
que
M. Viviani donna la même année 1692,
intitulé :
La Struttura, & Quadratura esatta dell'intero, e delle parti
d'un
nuovo Cielo ammirable, ed uno degli antichi, delle volte regolari degli
Architetti. Il y traite
tant en
Géométre, qu'en Architecte, des Voutes anciennes
des
Romains, & d'une Voute nouvelle qu'il avoit
inventée, &
qu'il nommoit Florentine.
Il
avoit souvent rappelé la Géométrie
à
l'usage des Arts, & il en préféroit
l'utilité
à une excessive sublimité ."
Quelques remarques s'imposent:
- A.D. PIO LISCI PUSILLO GEOMETRA est un anagramme de POSTREMO GALILAEI DISCIPULO. Galilée aimait ce genre de jeux -dans sa correspondance avec Kepler, par exemple- et Pascal avait lui aussi eu recours à un pseudonyme en lançant son défi sur la cycloïde.
- Ce texte est un défi de "géomètre à l'ancienne" (déjà!) à ceux de la nouvelle vague, tenants du Calcul Différentiel naissant (et loin d'être alors d'une limpidité à toute épreuve): c'est le sens à donner au premier paragraphe. On en perçoit l'ironie, puisque Viviani, tenant de la "Pure Géométrie" a une solution dans sa poche...
- Si le problème figure dans un ouvrage à vocation architecturale, le problème n'en est pas moins... imaginaire. On évoque parfois l'étude de la coupole du Duomo de Florence: il suffit de l'observer (notre fond de page) pour voir qu'elle n'a rien d'hémisphérique; d'autre part elle fut conçue en 1418 par Brunelleschi... Que Viviani ait, souvent, été consulté par les Médicis sur des questions de travaux publics ne peut justifier un tel anachronisme! Un "temple à la Féconde Géométrie" est encore une façon pour l'auteur d'affirmer le camp qu'il a choisi.
- Tel qu'il est posé, le problème est en fait très indéterminé. La solution de Viviani aura pour aire 4R2, ce qui répond au problème; mais on conçoit qu'au prix de courbes "plus compliquées" on puisse obtenir d'autres multiples rationnels de R2 .
"La" Courbe Solution
Le mérite de Viviani est d'obtenir sa solution de manière très élémentaire, par intersection de deux surfaces les plus simples possibles: une sphère et un cylindre tangents dont les rayons sont dans un rapport de 2 à 1. L'opération est symétrisée avec un deuxième cylindre tangent en un point diamétralement opposé de la sphère, afin d'obtenir les quatre ouvertures souhaitées. |
|
| Courbe de Viviani; (S1)
et (S1)
sont tangentes en S. (dessin manuel de l'auteur) |
Application
au "temple de la féconde Géométrie" Image de R. Caddeo, S. Montaldo et P.Piu dans [ 3 ] |
On peut imager l'opération de manière très simple: et très parlante pour le non-mathématicien: c'est le résultat de l'action d'un dénoyauteur à cerises (indispensable à la réalisation d'un bon clafoutis), (S1) sur la figure ci-dessus, dont la perforation n'est pas centrée sur un axe de la sphère (S2), mais la frôle tangentiellement...
Pour les amateurs d'équations, précisons ces deux formes, en coordonnées cartésiennes d'origine O, centre de la sphère, puis en coordonnées sphériques: θ, φ désignant respectivement longitude et latitude, il suffit de faire θ = φ dans la représentation de la sphère en coordonnées sphériques.
|
|
||
| Coordonnées
cartésiennes d'origine O |
Paramétrage |
Du
paramètrage, on tire facilement
R x = R2
(1 - sin2 θ)
= R2 - z2
ce
qui place la courbe sur un cylindre parabolique de direction (Oy). On obtient
d'ailleurs le même résultat en retranchant membre
à membre les deux équations
cartésiennes du cylindre et de la sphère. On
connait ainsi deux projections, sur (xOy) et (xOz); on
achève la détermination de la projection frontale
-ie sur (yOz) en
éliminant x
entre les deux équations; il suffit pour cela de prendre le
système sphère-cylindre parabolique
définissant la courbe de manière
équivalente
et de reporter la deuxième dans la première; on trouve la définition équivalente
dont la première équation montre que la projection frontale est une lemniscate (nom générique des courbes en forme de 8), certes, mais pas de Bernoulli comme on pourrait être tenté de répondre trop impulsivement...
C'est ce qu'on appelle la lemniscate de Gerono ; toutefois son paramétrage y = (R/2) sin (2θ) ; z = R sin θ permet de la reconnaître aussi comme courbe de Lissajous particulière.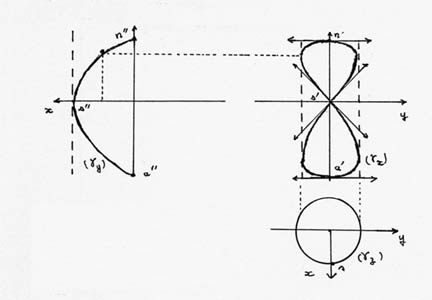
Une représentation "à la Monge", par l'épure des trois projections.
Quant au défi...apprenons ce qu'il en fut en reprenant notre lecture de la lecture de l'Éloge de Fontenelle:
Bref, en ce tournant de siècle, le Calcul Infinitésimal (plutôt le Calcul Intégral que le Calcul Différentiel, d'ailleurs, preuve que pour Fontenelle emploie indifféremment les trois dénominations) affirme son écrasante supériorité sur les méthodes géométriques basées sur des découpages, qui ont faitt les beaux jours des calculs d'aires planes d'Archimède à Cavalieri, en passant par Roberval et Pascal pour la Cycloïde). S'il a cru mettre les "Analistes" en difficulté, Viviani en est pour sa tentative... et Fontenelle de conclure avec élégance:
Quel joli nom pour le Calcul Infinitésimal, il est vrai inventé bien plus au Nord par Leibniz et Newton! Quant au calcul proprement dit, vous pouvez le trouver ici (fin de la page), par exemple, ou dans [2].
[2] montre également plusieurs façons d'usiner un modèle:
| x2 + y2 + z2 = R2 R x = R2 - z2 |
et de reporter la deuxième dans la première; on trouve la définition équivalente
| z4 + R2 ( y2 - z2
) = 0 R x = R2 - z2 |
dont la première équation montre que la projection frontale est une lemniscate (nom générique des courbes en forme de 8), certes, mais pas de Bernoulli comme on pourrait être tenté de répondre trop impulsivement...
C'est ce qu'on appelle la lemniscate de Gerono ; toutefois son paramétrage y = (R/2) sin (2θ) ; z = R sin θ permet de la reconnaître aussi comme courbe de Lissajous particulière.
Une représentation "à la Monge", par l'épure des trois projections.
Quant au défi...apprenons ce qu'il en fut en reprenant notre lecture de la lecture de l'Éloge de Fontenelle:
"Il marquoit que l'on attendoit
cette Solution de la Science secrète des illustres Analistes
du tems. Ce qu'il entendoit par cette Science
secrète, étoit sans doute , la
Géométrie des Infiniments petits, ou le Calcul
différentiel, quà peine connaissoit-on de
Réputation en Italie.
Le Problème de M. Viviani fut en effet bientôt expédié par cette Méthode. M. Leibnits [sic] le solut le même jour qu'il le vit, & le donna dans les Actes de Leipsic [sic] en une infinité de manières, aussi bien que M. Bernoulli de Bâle. Le nom de M. le Marquis de l'Hôpital ne parut point alors dans les Actes, parce que la guerre l'avoit empêché de recevoir ce Journal. Mais l'envoyé de Florence à Paris lui ayant proposé cette Enigme qui étoit sur une feuille volante, M. de l'Hôpital lui en donna aussitôt trois solutions, & lui en auroit donné une infinité d'autres, sans la trop grande facilité qu'il y trouva ."
Le Problème de M. Viviani fut en effet bientôt expédié par cette Méthode. M. Leibnits [sic] le solut le même jour qu'il le vit, & le donna dans les Actes de Leipsic [sic] en une infinité de manières, aussi bien que M. Bernoulli de Bâle. Le nom de M. le Marquis de l'Hôpital ne parut point alors dans les Actes, parce que la guerre l'avoit empêché de recevoir ce Journal. Mais l'envoyé de Florence à Paris lui ayant proposé cette Enigme qui étoit sur une feuille volante, M. de l'Hôpital lui en donna aussitôt trois solutions, & lui en auroit donné une infinité d'autres, sans la trop grande facilité qu'il y trouva ."
| |
|
| Croquis de Leibniz |
Croquis de Bernoulli |
Bref, en ce tournant de siècle, le Calcul Infinitésimal (plutôt le Calcul Intégral que le Calcul Différentiel, d'ailleurs, preuve que pour Fontenelle emploie indifféremment les trois dénominations) affirme son écrasante supériorité sur les méthodes géométriques basées sur des découpages, qui ont faitt les beaux jours des calculs d'aires planes d'Archimède à Cavalieri, en passant par Roberval et Pascal pour la Cycloïde). S'il a cru mettre les "Analistes" en difficulté, Viviani en est pour sa tentative... et Fontenelle de conclure avec élégance:
"Il
est facile de juger qu'avec de pareilles dispositions, quoiqu'il
eût été nourri dans l'ancienne
Géométrie, & qu'il fut d'un Pays si plein
d'esprit,
il auroit reçu sans répugnance, s'il eut
vécu plus
long tems, la nouvelle Géométrie du Septentrion
[...]."
Quel joli nom pour le Calcul Infinitésimal, il est vrai inventé bien plus au Nord par Leibniz et Newton! Quant au calcul proprement dit, vous pouvez le trouver ici (fin de la page), par exemple, ou dans [2].
[2] montre également plusieurs façons d'usiner un modèle:
- la manière de Viviani d'abord, à partir d'un bloc de bois parallélépipédique dans lequel on a percé deux trous cylindriques tangents, l'extérieur étant ensuite poli pour obtenir la sphère;
- une réalisation récente en aluminium.
Aussi sur un Cône, Pourquoi?
On peut, certes, continuer à manipuler les équations. Celles des cônes étant plus aisées à établir... ou à reconnaître (annulation d'une fonction homogène) quand l'origine est au sommet, on commence par translater le repère en S (R,0,0) ; notant X, Y, Z les coordonnée dans ce nouveau repère, les équations de la sphère et du cylindre deviennent
|
|
| Coordonnées
cartésiennes d'origine S |
Une combinaison évidente (retrancher à la première deux fois la seconde) permet de définir la courbe comme intersection du cylindre et d'un cône, reconnu comme promis à l'homogénéité de l'équation
|
|
| Coordonnées cartésiennes d'origine S |
Reste à en voir l'intérêt. C'est une technique inventée par Monge, dans sa Géométrie Descriptive, pour trouver les tangentes à l'intersection de deux surfaces en un point où elles ont même plan tangent. Clairement, en ce cas, le théorème : " La tangente en M à la courbe d'intersection de deux surfaces est l'intersection de leurs plans tangents respectifs en M" ne s'applique plus; c'est ici le cas en S.
Monge a alors l'idée de prouver que "la tangente au sommet du cône à un arc tracé sur celui-ci est encore une génératrice du cône". C'est facile analytiquement, mais un argument "d'époque" -si l'on ose dire- est le suivant: pour tout point P de la courbe voisin de S, la sécante SP est une génératrice; sa limite, qui est la tangente en S, en est encore une.
Dès lors, la tangente à tout arc passant par S est située:
1) sur le cône de sommet S et directrice la courbe de Viviani (nous venons d'en obtenir l'équation par manipulation élémentaire);
2) dans le plan tangent en S au cylindre (commun avec la sphère).
Les tangentes sont donc les génératrices d'intersection du cône avec ce plan, ce qui en fournit la construction sans aucun calcul!
Quelle réalité architecturale?
Commnençons par un constat amusé: la propre demeure de Viviani se prêtait fort mal à un passage à l'acte architectural de son idée; il s'en est donc bien gardé. Il n'est pas sûr qu'il y ait songé; ce n'était pour lui qu'un plaisant exercice de l'esprit.Néanmoins, trouver dans un monument une intersection sphère-cylindre exactement positionnée reste un défi intéressant, que le Mathouriste n'a pas encore été capable de relever. Examinons de plus près les contraintes:
- En extérieur, très peu de monuments exhibent une coupole sphérique. Il y a bien une intersection entre une sphère et deux cylindres... au Grand Palais à Paris; mais la biquadratique d'intersection des deux surfaces n'a pas de point double! Et notons que cela ne suffit pas: si les rayons ne sont pas dans le rapport 2:1 , on obtient "seulement" une hippopède d'Eudoxe...

Paris, Grand Palais. Deux cylindres, une sphère, une rencontre... mais pas celle que l'on souhaite!
- En intérieur, on peut observer beaucoup d'intersections cylindre-cylindre avec un point double et un plan tangent commun; mais la courbe d'intersection (bicylindrique) n'est pas sphérique et ne ressemble à celle de Viviani que par son aspect nodal! Mais beaucoup de coupoles à l'intérieur des églises, des mosquées....ont, en revanche, la forme sphérique, symbole de la perfection céleste, alors que leur aspect externe est plus allongé. Il n'y a plus qu'à leur faire rencontrer tangentiellement un cylindre de rayon moitié...
- Les auteurs de [ 3
] mentionnent -ils ne sont pas les seuls- l'intérieur de
l'église San Fedele à Milan.
La seule image disponible ne montre hélas
pas clairement la
chose -et du reste ne prétend pas la montrer (on la verra plus bas,
comparée à une photo de l'intérieur), c'est le moins qu'on puisse dire!
Le Mathouriste avait en vain lancé, en 2013, un appel aux nombreux mélomanes partis célébrer le bicentenaire de Verdi
à
la Scala de Milan, excellente occasion car
San Fedele en est à moins de deux minutes à pied, encore moins de la
galerie commerciale Vittorio Emmanuelle II, à peine plus du Duomo...
Les fanatiques verdiens ne doivent pas connaître With a littrle help from my friends, puisqu'aucune réponse ne lui parvint, et il ne restait plus au Mathouriste que
la solution d'y aller voir lui-même. Avec au cœur une légère
accélaration, il s'approcha de la place, dut ronger son frein et une
portion de pizza pour attendrela réouverture de l'église (les églises
italiennes ont la fâcheuse habitude de fermer pendant deux heures au
moins à l'heure du déjeuner...)
| Piazza San Fedele: vue générale, avec
au fond la façade d'entrée de l'église |
|

|
Aucun doute en entrant: on est
bien dans l'église représentée sur la gravure, tous les détails
coïncident: arches, colonnes, fenêtres à l'étage supérieur, petit
"kiosque" derrière l'autel, voutes sphériques (du moins peut-on
raisonnablement le supposer), décoration du plafond.... Mais où diable (si tant est que le mot convienne à l'endroit...) pourrait-il y avoir une fenêtre de Viviani? Ce dessin est, au demeurant, de bonne qualité dans sa représentation en perspective. S'il en fait voir une, cest que deux arcs dessinés se rejoignent à gauche de l'image, non par illusion perspective, mais dans la réalité; de quoi laisser sceptique avant même d'avoir fait le voyage. Pour être franc, leMathouriste n'a jamais été convaincu que cette gravure montrât quoi que ce soit, mais l'intime conviction n'a pas cours en mathématiques, et quel juge trancherait sur un dossier aussi léger, où l'unique pièce ne se laisse guère lire cliarement? |
|
| "Le" dessin de l'intérieur de San Fedele (source inconnue) |
Mais une quasi-réalité sculpturale!
Il n'y a
quand-même pas que l'Italie, pas que la vieille Europe... Une
fenêtre de Viviani, le Mathouriste
en a trouvé une (ou presque) devant le nouvel Hôtel de ville de Dallas
(conçu par I.-M.
Pei
en 1964 et achevé en 1978). Et même deux! C'est
une sculpture flottante
signée par Marta
Pan, artiste Française d'origine
Hongroise, qui n'en était pas à son premier essai
du genre.
Bon, on sait ce que le lecteur sourcilleux va dire: ce n'est pas tout à fait une fenêtre de Viviani. Il objectera que l'angle de la photo cherche à favoriser l'illusion. Mais cette illusion n'est rien d'autre que celle que produit l'éloignement de l'oeil, naturel quand on déambule autour du plan d'eau. D'ailleurs, le Mathouriste n'a rien à cacher, et, au prix d'un peu de patience (la rotation des sphères sur elle-même se fait aux caprices de l'eau et du vent, et cela fait partie du charme même de l'œuvre), il a pu réaliser une vue frontale du nœud:
On nous accordera que ce n'est pas loin du tout, et qu'il faut prendre en compte les contraintes mécaniques de la réalisation (trop de fragilité au point nodal). Le Mathouriste serait prêt à parier que l'intention de l'artiste, le premier croquis avait un point nodal. Et il est clair qu'une génératrice du cylindre est un diamètre de la sphère. Bref, c'est indiscutablement la réalisation artistique la plus proche!
Que les amateurs de surfaces ne quittent pas les lieux sans aller caresser l'autre sculpture, d'Henry Moore (à gauche sur la vue centrale)...
| |
||
| Dallas, Texas (USA): le City Hall et la sculpture flottante de Marta Pan | ||
Bon, on sait ce que le lecteur sourcilleux va dire: ce n'est pas tout à fait une fenêtre de Viviani. Il objectera que l'angle de la photo cherche à favoriser l'illusion. Mais cette illusion n'est rien d'autre que celle que produit l'éloignement de l'oeil, naturel quand on déambule autour du plan d'eau. D'ailleurs, le Mathouriste n'a rien à cacher, et, au prix d'un peu de patience (la rotation des sphères sur elle-même se fait aux caprices de l'eau et du vent, et cela fait partie du charme même de l'œuvre), il a pu réaliser une vue frontale du nœud:
On nous accordera que ce n'est pas loin du tout, et qu'il faut prendre en compte les contraintes mécaniques de la réalisation (trop de fragilité au point nodal). Le Mathouriste serait prêt à parier que l'intention de l'artiste, le premier croquis avait un point nodal. Et il est clair qu'une génératrice du cylindre est un diamètre de la sphère. Bref, c'est indiscutablement la réalisation artistique la plus proche!
Que les amateurs de surfaces ne quittent pas les lieux sans aller caresser l'autre sculpture, d'Henry Moore (à gauche sur la vue centrale)...
Des confusions à éviter
La courbe de Viviani est si présente dans l'esprit des mathématiciens qu'on a envie de la voir dès qu'une forme un peu ressemblante saute aux yeux. Gare donc aux "fausses amies":- les intersections cylindre-cylindre mentionnées ci-dessus;
- les loxodromies d'une sphère (courbes faisant un angle constant avec les lignes de niveau, ici à 45°; ou encore avec les méridiens.).
- les hélices sphériques (courbes faisant un angle constant de 45° avec la verticale, ou les plans horizontaux.)

|
 |
| Source: Article Wikipedia |
Source: Arup, constructeur du musée |
En effet, si l'on observe la structure tubulaire (photo de droite), on constate qu'à chaque point où ces lignes rencontrent les méridiens, l'angle est manifestement de 45°. .
Les côtés des quadrilatères curvilignes forment une version discrétisée d'une courbe qui vérifierait cela en tout point; naturellement seul l'éloignement crée l'illusion visuelle d'une courbe lisse! Les architectes qui cherchent un tel effet ne s'en cachent pas (voir par exemple [5]); c'est la longue tradition qui part du calcul de π par Archimède et aboutit à l'illusion de voir des courbes lisses sur nos écrans d'ordinateur (et plus l'acran comporte de pixels, meilleure elle est) en passant par la définition du ds² selon Leibniz, qui applique à un triangle curviligne infinitésimal le théorème de Pythagore pour un triangle ordinaire.
Le modèle à chercher est donc une courbe dont le vecteur unitaire tangent en tout point ferait lun angle de 45° avec les méridiens (ou les parallèles); un calcul en coordonnées sphériques fournit.
|
|
|
θ = - ln (tan φ/2) + θ0 |
Ces courbes ne sont pas algébriques (en raison de la présence du ln, notamment) et ne s'obtiennent donc pas par intersection de surfaces du second degré; ce qui interdit qu'il s'agisse de courbes de Viviani.
Références
- La Fenêtre de Viviani, sur le site www.mathcurve.com (Robert Ferréol)
- R. CADDEO, G. FRANZONI, Building Viviani's Windows (Conférence Aplimat 2006)
- R. CADDEO, S. MONTALDO, P. PIU, The Möbius Strip and the Viviani's Windows in Math Intelligencer , vol 23, 2001
- B. FONTENELLE, Éloge de Monsieur Viviani sur le site de l'Académie des Sciences .
- M. FREIBERGER, Perfects Buildings: the Maths of Modern Architecture in Plus Magazine .
- F. GOMES TEXEIRA, Traité des Courbes Spéciales Remarquables, tome 2 (Gabay)
- IREM, Aux Origines du Calcul Infinitésimal (Ellipses)
- D. LANNIER, La Nouvelle Analyse et la Géométrie ou Enquête sur la Fenêtre de Viviani. (1987)
Revenir à la Home Page du Mathouriste