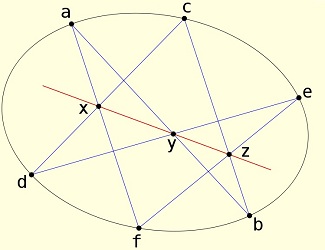
À quoi rêve donc Pascal?
Quel objet prioritaire est celui de sa méditation, dans
l'instant capté par l'artiste?
Tournons doucement autour du héros pour le
découvrir...
Mais oui! Sa vedette est une courbe géométrique:
la
Cycloïde,
ou, comme il l'appelait, la
Roulette.
Quand il s'y intéresse, en 1658, voilà longtemps
qu'il
n'a plus rien publié en Mathématiques; il est
retiré en religion et sa production est exclusivement
littéraire: Pensées et Lettres, toutes
ces choses
qu'il vient de délaisser brutalement, nous
suggère Pajou,
pour reprendre la Géométrie. Le lvret de
l'exposition de
1785 présentait les choses ainsi, orthographe curieuse
garantie
authentique (pourrait-on l'inventer?):
"Pascal
paraît occupé de la Sicloyde tracée sur
une table
qu'il tient de la main gauche, à ses pieds sont des feuilles
éparses contenant ses pensées, à
droite , un livre
ouvert où sont les Lettres."

|
Augustin Pajou (1730-1809), auteur de la statue de Pascal.
Selon les codes de son époque, il a
"résumé"
dans une seule sculpture les divers domaines d'activité du
personnage étudié.
Buste par son
contemporain et élève Philippe-Laurent Roland
(1746-1816)
Terre cuite
(1797), Musée du Louvre, Paris. |
Marguerite Périer, sa nièce, a
rapporté, dans ses
Mémoires sur son oncle, une anecdote largement
passée
à la postérité:
"il arriva qu'il lui vint un
très-grand mal de dents. Un soir M. le duc de Roannez le
quitta dans des douleurs très-violentes il se
mit au lit, et son mal ne faisant qu'augmenter, il s'avisa, pour
se soulager, de s'appliquer à quelque chose qui
pût lui faire oublier son mal. Pour cela, il pensa à
la proposition de la Roulette faite autrefois par le P. Mersenne,que
personne n'avait jamais pu trouver et à
laquelle il ne s'était jamais amusé. Il y pensa si bien qu'il en
trouva la solution et toutes les démonstrations.
Cette application sérieuse détourna son mal de dents, et quand il
cessa d'y penser il se sentit guéri de son mal. M.de Roannez étant
venu le voir le matin, et le trouvant sans mal, lui demanda ce qui
l'avait guéri. Il dit que c'était la
Roulette qu'il avait cherchée et trouvée"
Voici donc le moment de présenter cette courbe, son
histoire, et son lien avec Pascal.
Qu'est ce qu'une cycloïde?
Le
dispositif suivant, présenté dans l'exposition
Au delà du Compas, la
Géométrie des Courbes
conçue par F. Conti (Scuala Normale Supériore,
Pise) et
E. Giusti (Université de Florence) permet
à tout un
chacun d'en faire l'expérience:

|
Sur un disque, on marque un
point du bord (en rouge). On fait rouler sans
glisser
le disque sur la règle en bois du bas (celle du haut ne sert
qu'à caler le dispositif!) : le point, fixe sur le disque,
décrit sur le fond une courbe en arches successives (un tour
complet de la roue correspond à une arche). Ou,
comme le dit Pascal:
"La roulette est
une ligne si commune
qu'après la droite et la circulaire, il n'y en a point de si
fréquente;
et elle se décrit si souvent aux yeux de tout le monde,
qu'il y a lieu
de s'étonner qu'elle n'ait point été
considérée par les anciens, dans
lesquels on ne trouve rien: car ce n'est autre chose que le
chemin que
fait en l'air le clou d'une roue, quand elle roule de son mouvement
ordinaire, depuis que ce clou commence à s'élever
de terre, jusqu'à ce
que le roulement continu de la roue l'ait rapporté
à terre, après un
tour entier achevé. " |
 |
 |
Autrement dit, c'est ce que voit un spectateur immobile de la valve
d'une roue de bicyclette en mouvement uniforme.
On peut
voir des animations (et une
étude mathématique complète) sur le
site de Robert Ferréol,
www.mathcurve.com
ou
au musée Galilée
de Florence.
Elle n'était pas connue des Grecs, qui, pourtant, avaient
basé toute leur astronomie sur le mouvement analogue cercle
sur
cercle (la règle basse est remplacée par un
contour
circulaire); il est vrai qu'ils n'ont pas exhibé les courbes
du
mouvement, qui ne leur étaient pas utiles en soi.
Petite histoire de la Cycloïde
Pascal lui-même s'est chargé d'en
écrire une,
faisant le point avant son intervention, en quelque sorte. Ce texte est
daté du 10 Octobre 1658
On y retrouve, sans surprise, les protagonistes du débat sur
le
vide... les physiciens sont aussi mathématiciens! Lisons
donc
Pascal:
"Le
Feu Père Mersenne, minime, fut le premier qui la remarqua
environ l'an 1615, en considérant le roulement des
rouës, ce
fut pourquoi il l'appela la Roulette. Il voulut ensuite en
reconnoître la nature et les
propriétés, mais il ne
put y pénétrer. [...]
Il proposa
donc la recherche
de la nature de cette ligne à tous ceux de l'Europe qu'il en
crut capables, entre autres à Galilée; mais aucun
ne put
y réussir, et tous en
désespérèrent."
Au fait, quelles propriétés d'une courbe
cherche-t-on? Et
à quelles techniques modernes se rattachent-elles?
Les trois principales sont:
| Générales
|
Cycloïde |
Type
(moderne) du problème |
| Aire |
entre
une arche et la base |
calcul
intégral |
| Longueur |
d'une
arche |
calcul
intégral |
| Tangente
en point |
en
un point quelconque de la courbe |
calcul différentiel |
Oui, mais.... le calcul différentiel et intégral
ne sera
inventé qu'un peu plus tard, par la
génération
suivante de mathématiciens: Newton, Leibniz. Il faut donc
faire
preuve de beaucoup d'ingéniosité; l'un des
procédés les plus courants alors est la
Méthode
des Indivisibles de Cavalieri: c'est, en gros, celle que va employer le
premier vainqueur, Roberval, en 1634, pour la question de l'aire:
"En
effet M. de Roberval y réussit; il démontra que
l'espace
de la roulette est triple de la roue qui la forme. [...]
Il dit au père que sa question étoit
résolue, et
lui déclara même cette raison triple, en exigeant
néanmoins qu'il la tienne secrète durant un an,
pendant
lequel il proposeroit de nouveau cette question à tous les
géomètres.
Le père, ravi de ce succès, leur
écrivit à
tous, et les pressa d'y repenser, en leur ajoutant que M. de Roberval l'avait
résolue, sans leur dire comment.
L'année et plus étant passée, sans
qu'aucun en
eût trouvé la solution, le père leur
écrivit
pour la troisième fois, et leur déclara alors la
raison
de la roulette à la roue, comme 3 à 1.
En
1635, sur
ce nouveau secours, il s'en trouva deux qui donnèrent la
démonstration: on reçut leurs solutions presque
en
même temps, l'une de M. de Fermat, conseiller au parlement de
Toulouse, l'autre de feu M. Descartes, et toutes deux
différentes l'une de l'autre, et encore de celle de M.
Roberval."
Voilà un style typique des correspondances de ce
siècle,
qui perdurera aux débuts du calcul infinitésimal:
celui
du défi. On annonce avoir trouvé, on met les
autres au
défi d'en faire autant, et, grand seigneur (ou malicieux),
quand
ils sèchent, on les aide d'un petit renseignement
supplémentaire (ici, la solution du problème de
l'aire)...
Pascal mentionne alors la résolution de la question des
tangentes, à nouveau par Roberval:
"Ainsi,
la chose devint publique, et il n'y eut personne en France, de ceux qui
se plaisent à la géométrie, qui ne
sût que M. de Roberval étoit
l'auteur de cette solution, à laquelle il en ajouta en ce
même temps deux autres: l'une [...],
l'autre, l'invention des touchantes à cette ligne, par une
méthode qu'il trouva alos, et qu'il divulga incontinent,
laquelle est si générale, qu'elle
s'étend aux
touchantes de toutes les courbes: elle consiste en la composition des
mouvements."
C'est
ensuite le Pascal polémiste à l'humour cinglant
-bref, l'auteur des
Provinciales!-
que l'on retrouve dans la suite de son histoire:
"En 1638, feu M. de Beaugrand envoya [les solutions de
Roberval et Fermat] à Galilée, sans en nommer les
auteurs [...]. Galilée mourut
peu après, et M. de
Beaugrand aussi. Torricelli succéda à
Galilée, et
tous ces papiers lui étant venus entre les mains, il crut
qu'il
y avoit assez de temps passé pour faire que la
mémoire en
fût perdue, et ainsi il pensa à en profiter.
Il fit donc imprimer son livre en 1644, dans lequel il attribue
à Galilée ce qui est dû au
père Mersenne,
d'avoir formé la question de la roulette; et à
soi-même ce qui est dû à M. de
Roberval , d'en avoir donné le premier la
résolution: en
quoi il fut non seulement inexcusable, mais encore
malheureux; car ce fut un sujet de rire en France, de voir que Torricelli s'attribuoit en 1644, une invention qui
étoit publiquement et sans contestation reconnue depuis huit
ans pour être de M. de
Roberval, et dont il y avoit, outre une infinité de
témoins vivants, des témoignages
imprimés, et
entre autres un écrit de M. Desargues, imprimé
à
Paris au mois d'août 1640, avec privilège,
où il
est dit, que la roulette est de M. de Roberval, et que la
méthode de maximis et minimis est de M. de Fermat."
Certains
auteurs affirment toutefois que Galilée avait
posé le problème avant
Mersenne, vers 1600, voire même 10 ans plus tôt, en
l'appliquant aux
arches de ponts... On apprécierait une source
précise de ce point. Ne
se contentent-ils pas de reproduire ce qu'écrit d'Alembert
dans l'Encyclopédie?
"La
cycloïde est une courbe assez moderne ; & quelques
personnes en
attribuent l'invention au P. Mersenne, d'autres à
Galilée ; mais le
docteur Wallis prétend qu'elle est de plus ancienne date ;
qu'elle a
été connue d'un certain Bovillus vers
l'année 1500, & que le
Cardinal Cusa en avoit même fait mention long-tems
auparavant,
c'est-à-dire avant l'an 1451.
Il
est constant, remarque M. Formey, que le P. Mersenne divulgua le
premier la formation de la cycloïde, en la proposant
à tous les
géomètres de son tems, lesquels s'y appliquant
à l'envi, y firent alors
plusieurs découvertes; en sorte qu'il étoit
difficile de juger à qui
étoit dû l'honneur de la premiere invention.
Delà vint cette célebre
contestation entre MM. de Roberval, Toricelli, Descartes, Lalovera,
&c. qui fit alors tant de bruit parmi les savans."
|
Pascal et la Cycloïde
Évasif sur les circonstances de sa méditation
-plus que
sa nièce, en tout cas- voici comment Pascal introduit sa
propre
contribution au sujet. Il s'agit encore de questions qu'on
réglera après par l'emploi du calcul
intégral: la
détermination de divers centres de gravité de
portions de
courbes ou de surfaces dans lesquels intervient la fameuse courbe.
"La connaissance de la roulette
ayant été portée jusque-là
par M. de
Roberval, la chose étoit demeurée en cet
état
depuis quatorze ans; lorsqu'une occasion imprévue m'ayant
fait
penser à la géométrie que j'avois
quittée
il y avoit longtemps, je me formai des méthodes pour la
dimension et les centres de gravité des solides, des
surfaces
planes et courbes, auxquelles il me sembla que peu de choses pourroient
échapper: et pour en faire l'essai sur un sujet des plus
difficiles, je me proposai ce qui restait à
connoître de
la nature de cette ligne; savoir les centres de
gravité de ses solides, et des solides de ses parties , la
dimension et les entres
de gravité des surfaces de tous ces solides. [...]"
Fidélité à la tradition des
défis? Raison
de polémique religieuse comme le rapporte sa
nièce?
"M. de Roannez lui dit qu'il y
avait bien un meilleur usage à en
faire; que dans le dessein où il était de
combattre les
athées, il fallait leur montrer qu'il en savait plus qu'eux
tous
en ce qui regarde la géométrie et,ce qui est
sujet
à la démonstration et qu'ainsi s'il se soumettait
à ce qui regarde la foi, c'est qu'il savait jusques
où
devaient porter les démonstrations et sur cela, il lui
conseilla
de consigner soixante pistoles et de faire une espèce de
défi à tous les mathématiciens habiles
qu'il
connaissait et de proposer ce prix pour celui qui trouverait la
solution du
problème."
Toujours est-il que Pascal lance lui aussi un
défi, et redouble de malice en le faisant, plutôt
que sous
son identité propre, sous un nom d'emprunt. Et pas n'importe
lequel:
Amos
Dettonville, c'est-à-dire un anagramme
de
Louis
de Montalte... son pseudonyme d'auteur des
Provinciales!
Les contributions viennent effectivement de toute l'Europe -du
"réseau
Mersenne". En particulier, l'architecte de Saint-Paul à
Londres,
Christopher Wren, dont il ne faut pas oublier qu'il fut aussi
mathématicien, se distingue en résolvant le
problème de la longueur.... que Pascal n'avait pas
posé,
quoiqu'il ne fut pas encore résolu. Il ne manque pas de le
saluer élogieusement:
"Elles
sont de deux sortes. Les unes prétendent d'avoir
résolu
les problèmes proposés, et ainsi avoir droit aux
prix; [...]
Les autres n'ont point voulu prétendre à ces
solutions,
et se sont contentés de donner leurs premières
pensées sur cette ligne.
J'ai trouvé de belles choses dans leurs lettres, et des
manières fort subtiles de mesurer le plan de la roulette, et
entre autres dans celles de M. de Sluze, chanoine de la
cathédrale de Liège; de M. Richi, Romain; de M Huguens, Hollandois [...]
Mais entre tous les écrits qu'on a reçus de cette
sorte,
il n'y a rien de plus beau que celui qui a été
envoyé par M. Wren;
car outre la belle manière qu'il a de mesurer le plan de la
roulette, il a donné la comparaison de la ligne courbe
même et de ses parties avec la ligne droite: sa proposition
est
que la ligne de la roulette est quadruple de son axe, dont il a
envoyé l'énonciation sans
démonstration. Et comme
il est le premier qui l'a produite, c'est sans doute à lui
que l'honneur de la première invention en appartient."
Mais personne ne résoud les problèmes, et
Dettonville publie sa solution.
Un exemplaire...
adjugé chez Christie's New York pour 90
500 $ (Juin 1998)
Voici ce qu'en dit sa nièce:
" M.Pascal le crut et
consigna les soixante pistoles
entre les mains de M ****, nomma des examinateurs pour juger des
ouvrages qui viendraient de toute l'Europe et fixa le temps
à
dix-huit mois au bout desquels personne n'ayant trouvé la
solution suivant le jugement des examinateurs, M. Pascal retira ces
soixante pistoles et les employa à faire imprimer son
ouvrage
dont il ne fit tirer que cent-vingt exemplaires."
Marguerite
Périer
En écrivant à Huyghens, le 6 Janvier 1659, Pascal
entretient encore -jeu?- le mystère, et se retranche
derrière les problèmes techniques de la poste
pour ne
dévoiler, dans un premier temps, qu'une partie des
informations:
"
Tout ce que je puis est de vous envoyer autant qu'il vous plaira
d'exzmplaires du Traité de la Roulette, où
l'anonyme a
résolu les problèmes qu'il avait
lui-même
posés. Je ne vous en mets ici que qulques avant-coureurs,
car le
paquet serait trop gros pour la poste. Je m'informerai de nos libraires
de la voie qu'il faut tenir pour en envoyer commodément."
N'y voyons aucune rétention de l'information scientifique,
mais
une petite jouissance à exciter la curiosité de
son
correspondant. Un de ces jésuites qu'il combattit
infatigablement eût-il mieux tourné l'argument?
Pas
sûr... Huyghens, apparamment pas dupe, entre dans le
jeu et
répond le 5 Février
" à Monsieur Pascal,
sieur d'Ettonville"!

|

|
| Pajou
semble n'avoir pas bien observé la verticalité
des
tangentes aux extrémités de l'arche... |
et... Gournier non plus! |
Il semble
que le monument
Clermontois évoque la propriété de
Roberval:
étant donnée l'aire du disque qui roule, on la
double en
considérant un
demi-cercle
de rayon double, puis on la triple avec la roulette!
Actualité (2010):
Un manuscrit mathématique (en fait, un brouillon) de Blaise
Pascal a été découvert
parmi ceux des
Pensées
récemment par Dominique Descotes, professeur à
l'université de Clermont-Ferrand-CNRS. C'est la seule trace
écrite des preuves lié aux travaux sur
la
roulette dans les
Lettres
de A. Dettonville.
En savoir plus:
Chroniques de la BnF, n°56, p24
(2010).
Une Note Amusante -ou pathétique, pour finir:
Le titre
Histoire de la
Roulette,
joint à l'intérêt de Pascal pour le
Calcul des
Probabilités dans les jeux de hasard, a
égaré plus
d'un auteur de page web... C'est ainsi qu'on lit en de nombreux
endroits que la roulette (jeu de casino) a été
inventée par Pascal en 1655 (année de son
Histoire de la Roulette,
évidemment) alors qu'il semble plus raisonnable de la dater
du
XIXème siècle, en dépit
d'ébauches plus
anciennes de jeux du même genre. Mais en France, le mot
n'apparait pour la première fois qu'en 1716 (Hôtel
de Soissons, Paris). On n'aura pas la cruauté d'en
dénoncer
un en
particulier (encore que ceux qui affirment, dans leur délire
euphorique, qu'il était alors à la recherche d'un
mouvement perpétuel, le mériteraient bien!). On
s'étonnera presque qu'aucun n'ait fait le lien entre la
fameuse
rage de dents... et l'instrument du dentiste.
La Cycloïde après Pascal
L'histoire de la courbe ne s'arrête cependant pas
là: deux
autres problèmes,issus de la mécanique,
totalement
indépendants de la définition
géométrique
donnée, vont mener à
sa rencontre; par ordre d'apparition: celui de la
courbe
tautotochrone. celui de la
courbe
brachystochrone.
Retour n°1: la Tautochrone
C'est justement en Décembre 1659 que
Huyghens
(qui, rappelons le, a échangé des lettres avec
Pascal sur
la cycloïde depuis le début de l'année)
découvre deux propriétés, l'une
géométrique,
l'autre mécanique, de la
cycloïde dont il pense tirer parti pour améliorer
les
horloges à pendule. En effet, on saitdepuis 1638 (Mersenne)
que
les
oscillations d'un pendule
classique
ont une période qui dépend de l'amplitude
initiale, sauf
dans le cas des petites oscillations (mais ce n'est qu'une
approximation); d'autre part, l'amortissement pose le
problème
de la manière d'entretenir les oscillations (poids, puis
ressorts)
- Géométrie:
les normales à la cycloïde sont
elles-même tangente
à une cycloïde de mêmes dimensions
(mathématiquement, on dit que la développée
d'une cycloïde est une autre cycloïde). Sa
démonstration est purement géométrique
.
- Mécanique:
si l'extrémité d'un pendule décrit une
cycloïde, ses oscillations sont isochrones,
c'est à dire indépendantes de l'amplitude. On dit
que la cycloïde est une courbe tautochrone. En
ce cas, l'amortissement
n'et plus un problème!
La propriété géométrique
donne une moyen
d'avoir ce résultat Il suffit pour cela que le
fil soit guidé par deux joues cycloïdales:
Huyghens, qui
d'abord avait pensé à des joues circulaires,
rélise le parti qu'il peut tirer de l'
Histoire de la Roulette que
lui a communiqué Pascal!

|
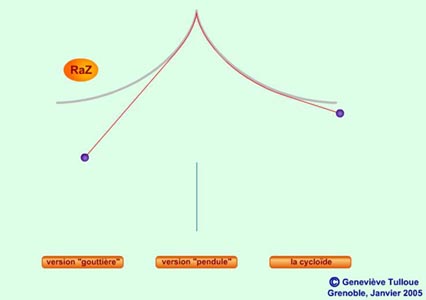
|
Dans l'Astronomie
Populaire
de François Arago . |
Démonstration
animée par G.Tulloue (Université de Nantes)
Partant de position choisies par
le lecteur (cliquer sur RaZ, dépklacer les boules), les deux
pendules se croisent toujours sur la ligne!
|
Voici des
images de
Huyghens lui-même, montrant les fameuses joues (n'hésitez pas à
aller les voir... chez lui!).
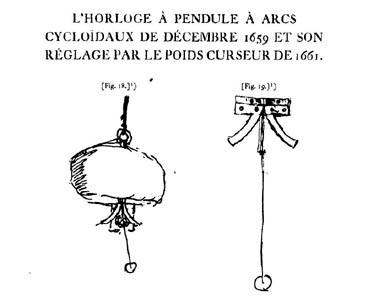
|

|
 |
| Croquis manuscrits de Huyghens
(Œuvres); figure in Horologium
oscillatorium sive de motu pendularium (1673) |
Noter que
le problème résolu était
(relativement!) facile:
partir de la
cycloïde, et constater qu'elle a ses
propriétés.
Il aurait été bien plus redoutable
- de poser le problème "
chercher les
courbes ayant cette propriété" (sans
idée préalable du résultat);
- de prouver que c'est
la seule
courbe ayant cette propriété
C'est précisément un problème de ce
type que l'on
va rencontrer maintenant, et, comme on va le constater, la
non-connaissance a priori de la solution va rendre le travail bien plus
périlleux.
De plus, pour aller au delà de deviner le
résultat, l'outil du calcul différentiel sera
indispensable.
"It was in the left hand try-pot of
the Pequod, with the soapstone diligently circling round me, that I was
first indirectly struck by the remarkable fact, that in geometry all
bodies gliding along the cycloid, my soapstone for example, will
descend from any point in precisely the same time."
Herman Melville, Moby Dick,1851
Cette référence littéraire vous surprend? Lisez
cet article de Michèle Audin (site
Images des Mathématiques, CNRS)
Retour n°2: la Brachystochrone
Il s'agit de découvrir la courbe de plus rapide descente
entre
deux points fixés: quelle forme donner au toboggan pour
être le premier en bas? Là, pas de toute:
Galilée
est le tout premier à aborder le problème, en
1635. Mais
si Pascal ne le mentionne pas, il y a une bonne raison: à ce
moment là, la cycloïde est totalement hors jeu!
"Au premier coup
d'œil, on est porté à croire que la
ligne droite, comme le plus court chemin d'un point à
l'autre,
doit être aussi le chemin de la plus vite descente; mais le
géomètre attentif s'abstient de prononcer,
lorsqu'il
considère que, dans une courbe concave, décrite
d'un
point à l'autre, le mobile descend d'abord plus
verticalement,
et acquiert par conséquent une plus grande vitesse que sur
le
simple plan incliné, ce qui produit une compensation et peut
faire arriver le corps plus promptement suivant la ligne courbe que
suivant la ligne droite. La métaphysique seule ne peut donc
pas résoudre la question, et il fallait absolument
recourir
à un calcul précis."
La fausse solution de
Galilée:
Elle figure
dans son étude du
mouvement uniformément
accéléré, dans la
"troisième journée" de ses Discours sur deux Sciznces
Nouvelles.
Elle commence par une preuve, tout à fait correcte,
comparant
les temps mis pour joindre les deux extrémités de
la
corde sous-tendant un quart de cercle et d'une ligne brisée
de
deux segments.
 |
 |
"Si
du point le plus bas d'un cercle vertical on
élève un
plan incliné sous-tendant un arc égal
à un
quadrant, et si des extrémités de ce plan on
mène
deux autres plans vers un point quelconque de l'arc, alors le temps de
descente le long de ces deux derniers pris ensemble sera plus bref que
sur le premier plan, ou que sur l'un des deux seulement, à
savoir le plan inférieur"
Avec
les notations de la figure, le temps de parcours de DB puis BC est plus
court que le long de DC.
(les autres notations et construction servent à sa preuve
géométrique)
|
| frontispice |
Proposition
et figure associée |
|
C'est ensuite que les choses se gâtent:
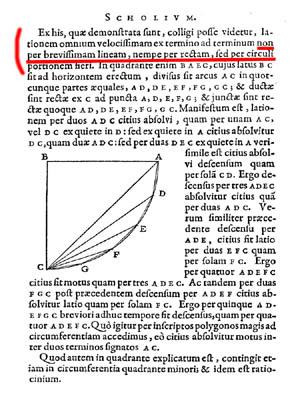
|
"SCHOLIE:
D'après les démonstrations
précédentes, il
semble possible de conclure que le mouvement le plus rapide entre deux
points n'a pas lieu entre la ligne la plus courte, soit la droite, mais
par un arc de cercle."
Galilée
partage le quart de cercle en arcs égaux, AD, DC,...GC. Le
résultat acquis lui permet de dire que l'on va plus vite le
long
de AD puis DC que selon AC;
"Mais si le
mobile part
du repos en A, il parcourt plus rapidement DC que les deux cordes AD et
DC, et partant toujours du repos en A, il est vraisemblable qu'il
descend plus vite le long des deux cordes DE et EC que le long de DC
seul; il franchit par conséquent plus rapidement les trois
cordes AD,DE,EC, que les deux cordes AD et DC. [...]
et ainsi la descente a lieu plus rapidement le long des cinq cordes
ADEFGC que le
long des quatre cordes ADEFC. On voit donc que plus on se rapproche de
la circonférence en augmentant le nombre des
côtés
des polygones inscrits, plus le mouvement s'accomplit rapidement entre
les deux points donnés A et C.
|
D'abord, il y a
le passage de 2 côtés à 3: on part de D avec une vitesse
initiale, alors que sa comparaison pour AC et ADC se faisait
à vitesse initiale nulle.
Et de toutes façons, le procédé de
"passage
à la limite géométrique", pour
ingénieux
qu'il soit (mais il remonte à
Archimède) peut tout
juste prouver que la descente sur le cercle est plus rapide que sur
tous les polygones, pas que c'est
LA plus rapide! Elle minimise parmi un ensemble
restreint de trajectoires possibles (polygones et cercle),
pas parmi
toutes les trajectoires possibles.
|
En 1697,
Johann Bernoulli
(1667-1748) pose le problème à ses pairs; il
s'agit cette
fois de tester la puissance du calcul différentiel
naissant...
et l'habileté de ceux qui le manient. Dans la forme,pas de
différence avec l'époque de l'Académie
de
Mersenne, c'est un défi, à tous en
général,
à
son frère Jakob
(1654-1705) en particulier!
"Les
sciences ont donc une obligation de la plus haute importance
à Jean Bernoulli, d'avoir attiré l'attention des
géomètres sur cette théorie
générale, en leur proposant le
problème de la
Brachistocrone [...]."
"Leibniz résolut le problème le jour
même qu'il reçut le programme de Jean
Bernoulli, à qui il donna aussitôt avis: tous deux
convinrent de tenir leurs solutions cachées, et d'accorder
un an
aux autres géomètres pour s'exercer sur une si
belle
question. Ce délai fut annoncé dans les journaux
et dans
une feuille volante que Jean Bernoulli envoya de tous
côtés.
Il n'était pas encore expiré, lorsqu'outre les
solutions de
Jean Bernoulli et de Leibnitz, il en parut encore trois autres, dont
les auteurs étaient étaient Neuton [sic!], le
marquis de
l'Hôpital et Jacques Bernoulli. Celle de Neuton parut anonyme
dans les Transactions Philosophiques de la
Société Royale
de Londres, mais Jean Bernoulli devina l'auteur [...]. Le marquis de
l'Hôpital eut beaucoup de mal à trouver la sienne [...]. Enfin Jacques
Bernoulli donna, avant l'expiration du terme prescrit par son
frère, une solution où il démontre que
la courbe
demandée est un arc de cycloïde."

|

|
Dispositif
montrant que la cycloïde "bat la droite": deux billes sont
lâchées simultanément par un volet, en
haut de
l'appareil. On juge l'arrivée en un point bas
réglable...
il n'y a vraiment pas photo!
(conçu et réalisé par E. Giusti et F.
Conti pour l'exposition Au delà du Compas. ) |
La solution... intuitive
de Johann Bernoulli:
 |
La solution initiale de Johann
Bernoulli repose sur une idée classique en calcul intégral: découper le plan
en fines lamelles (discrétisation, puis
passage à la limite)
dans lesquelles la trajectoire est si petite qu'on peut
considérer que
c'est un segment.
Mais comment passer d'une tranche à l'autre? Il a
l'idée d'appliquer les lois
de la réfraction de Snellius et Descartes,
parce qu'elles guident la lumière dans les milieux
inhomogènes, selon le principe d'optimalité de
Fermat:
"si nous
voulions employer dans cette recherche ce principe si commun et si
établi que la
nature agit toujours par les voies les plus courtes, nous
pourrions facilement y trouver notre compte."
Ce n'est
donc qu'une analogie
ingénieuse entre deux problèmes
d'optimisation, l'un optique, l'autre mécanique... mais elle
lui fournit la solution!
|
|
La solution initiale de Jakob Bernoulli était meilleure, il
en
était persuadé, et comme sur un terrain de rugby,
le
défi entre
gentlemen...
vira à la bagarre!
"La
rivalité de gloire qui divisait depuis longtemps les
frères Bernoulli se déploya toute
entière en cette
occasion: elle avait été d'abord un peu
tempérée par l'habitude de se voir, au moins de
temps en
temps, et par l'entremise d'amis communs; mais le cadet ayant
été nommé professeur de
mathématiques
à Groningue, en 1695, ils ne consevèrent
bientôt
plus de relations particulières; ils ne se parlaient plus
que
dans les journaux, et c'était poue se proposer les
problèmes les plus difficiles. Jean Bernoulli
était l'agresseur; mais peut-être son
frère
avait-il montré un peu trop de hauteur dans sa
première
réponse qu'il lui fit [...]. Dans ces dispositions, Jacques
Bernoulli voulant enfin se venger d'une manière
éclatante, mais en même temps utile à
la
géométrie, provoqua nomminativement son
frère
[...].
Johann, inconscient de ses propres insuffisances et du
caractère
beaucoup plus général de son frère, le
"chambrait"
sur son délai de réponse:
"Quelques
difficiles que ces problèmes paraissent, je 'ai pas
manqué de m'y attacher à l'instant même
que je les
ai reçus; mais voyez avec quel succès! Au lieu de
trois
mois que l'on me donne pour sonder le gué, et au lieu de
tout le
reste de cette année pour trouver la solution, je n'ai
employé, en tout, que trois minutes de temps pour tenter,
commencer et achever d'apporfondir tout le mystère."
Jakob était assez sûr de lui pour proposer des
paris en
espèce sonnantes; Johann rectifia sa solution en
concédant
"une
trop grande précipitation", ce qui ne calma pas
Jakob:
"Je
prie mon frère de repasser tout nouveau sur sa
dernière
solution, d'en examiner attentivement tous les points, et de nous dire
ensuite si tout va bien, lui déclarant qu'après
que
j'aurai donné la mienne, les prétextes de
précipitation ne seront plus écoutés"
Le ton monta encore, et, comme au rugby, on dut faire appel
à
l'arbitre, M. Leibniz, et à ses assistants, MM. Newton et de
l'Hôpital. On reconnut la meilleure qualité et la
plus
grande généralité du travail de Jakob;
mais il
faudrait attendre ceux d'Euler et Lagrange pour parvenir à
la
solution moderne du problème ("Calcul des Variations").
"Ainsi, Jean Bernoulli trouva, par analogie,
une solution accidentelle d'un problème. Jacques
Bernoulli développa une méthode
géométrique
pour la résolution des problèmes analogues. Euler
généralisa à la fois les
problèmes et la méthode géométrique.
Lagrange enfin se
libéra complètement de la
considération des figures et donna une méthode
analytique."
E. Mach,
La
Mécanique,Exposé Historique et Critique de son
Développement (1883)
La Cycloïde aujourd'hui
On en parle encore!
D'abord, dans des articles récents (2011,2012) de
R.M. Mottola relatifs à la construction des violons des célèbres luthiers de Cremone:
article 1,
article 2 dans le
Savart Journal (Science and technology of stringerd musical instruments).
Ensuite, dans le choix architectural des voûtes du
Kimbell Art Museum de Fort Worth (Texas, USA), conçu en 1966 (achevé en 1972) par
Louis Kahn. Ce qui a fait l'objet d'un
article du
Mathematical Intelligencer.
 (source Wikipedia)
(source Wikipedia)Références
Générales, Sources
- Blaise PASCAL, Œuvres Complètes, édition 1779 (Bossut ed), tome 5: Mathématiques (Google)
- Blaise PASCAL, Œuvres Complètes, édition 1864, tome 3: Physique et Mathématiques (Google)
- Blaise PASCAL, Histoire de la Roulette et... Suite de l'Histoire de la Roulette (Gallica BnF)
- Blaise PASCAL, Récit de l'examen et du jugement des escrits envoyez pour les prix, proposez publiquement sur le sujet de la "roulette... (Gallica BnF)
- Blaise PASCAL, Lettres
de A. Dettonville : contenant quelques-unes de ses inventions de
geometrie. (Gallica BnF)
Coniques, Hexagramme mystique
- Blaise PASCAL, Essay pour les Coniques (Gallica BnF)
- Jean LEFORT, Pascal (IREM Strasbourg). Pour voir la V.O. de l'hexagramme... quand il n'était qu'un quadrilatère!
- P. COSTABEL, Notes de Leibniz sur les "Coniques" de Pascal in Revue d'histoire des sciences et de leurs applications, 1962, Tome 15 n°3-4. pp.253-268.
- Jean ITARD, «L'introduction à la Géométrie » de Pascal in Revue d'histoire des sciences et de leurs applications, 1962, Tome 15 n°3-4. pp. 269-286
- René TATON, L'Œuvre de Pascal en Géométrie Projective, in Revue d'histoire des sciences et de leurs applications, 1962, Tome 15 n°3-4. pp. 197-252
Cycloïde
- La Cycloïde, sur Wikipedia: animations, courbes "voisines", liens.
- La Cycloïde, sur le site www.mathcurve.com (Robert Ferréol)
- P. COSTABEL, Essai sur les Secrets des Traités de la Roulette in Revue d'histoire des sciences et de leurs applications, 1962, Tome 15 n°3-4. pp. 321-350.
- L. SCHELER, Les Lettres de Dettonville offertes à Jean-Baptiste Colbert in Revue d'histoire des sciences et de leurs applications, 1962, Tome 15 n°3-4. pp. 351-365.
- C. MERKER, Le Chant du Cygne des Indivisibles, le Calcul Intégral dans l'Œuvre de Pascal (PUF): pour mieux suivre Pascal et sa manière.
- J.-L. VERLEY, Autour de la Cycloïde (congrès Maths en Jeans 1994)
- P. AUDIN, Brachistochrone, la Naissance du Calcul des Variations Quadrature n°1 (Novembre-décembre 1989)
- J.-L. CHABERT, Le Problème Brachystochrone in IREM, Histoire de Problèmes, Histoire de Mathématiques (Ellipses)
- J. COOLIDGE, A History of Geometrical Methods (Dover)
- F. GOMES TEXEIRA, Traité des Courbes Spéciales Remarquables, tome 2 (Gabay)
- R. PROCTOR, A Treatise on The Cycloid and all forms of Cycloidal Curves (en ligne, Cornell University)