Retour
à Metz
De 1815 à 1825 à Metz, il revient à
l'École d'application de l'Artillerie et du Génie
de Metz, comme officier du
génie -capitaine en 1822 lorsque parait la
première édition de son livre- mais aussi comme
ingénieur mécanicien, puis, à
l'initiative d'Arago, Professeur de
Mécanique en 1824 ; il laisse d'ailleurs son nom
à un système de pont-levis et surtout
à une
turbine à aubes courbes
Pour plus de détails sur ce point, voir cet
historique (et plus
généralement ce
site) concernant les
généralités, et sur
l"apport de notre héros, téléchargez,
en suivant le lien ci-dessous, l'article de Bruno BELHOSTE et Louis
LEMAITRE
J.-V.PONCELET, Les Ingénieurs
Militaires et Les Roues et Turbines
Hydrauliques .
Poncelet participe activement à la vie de sa ville. En
particulier, il est, dès sa fondation le 14 Mars 1819,
membre de la
Société
Académique de Metz.

|

|

|
| Depuis sa fondation, la
Société a toujours eu son siège au 20
en Nexirue, à Metz |
Son
Bulletin (numéro contenant l'hommage
à Poncelet) |
Il en est
même le
président en 1823-24; il y fait de nombreuses communications
sur la Géométrie et la Mécanique.

Le 1er Mai 1848, lors de l'élection des
représentants à l'Assemblée
Constituante, le département de Moselle le nomme
représentant du peuple, à la quasi
-unanimité, et sans qu'il l'ait demandé!
Aussi,
un mois à peine après son
décès, le Conseil Municipal
"par un vote unanime du 25
Janvier 1868, approuvé par décret
impérial du 8 Février suivant, a
décidé que la rue sur laquelle est l'École d'application,
et la plus voisine de celle où habitait le
Général, porterait désormais le nom de
Rue Poncelet.
"
La Rue Poncelet, à
l'extrémité qui donne sur l'École
d'application de l'Artillerie et du Génie. Remarquer la
plaque commémorative sur le pilier droit.
La demeure de Poncelet à laquelle fait allusion le texte
précédent se trouvait 18, rue de l'Esplanade:
elle bordait l'esplanade (sur laquelle est située la statue
du maréchal Ney). Celle-ci est, par la suite,
devenue Avenue Winston Churchill... et, comme l'allure s'est
passablement modifiée, il n'y a plus aucune trace de la
maison de Poncelet. Pas même un numéro 18,
d'ailleurs!
La Rue Poncelet, à
l'extrémité qui donne sur l'École
d'application de l'Artillerie et du Génie. Remarquer la
plaque commémorative sur le pilier droit.
et Paris,
pour finir
Puis, en 1838 il est chargé de
créer le cours de Mécanique Physique et
Expérimentale à la Sorbonne à Paris.
Dés lors, sa carrière se poursuit dans la
capitale; il est nommé général le
1/07/1848 par Arago et, dix jours plus tard, Commandant de
l'École Polytechnique de
1848 à 1851. On y trouve son buste... quelque peu
caché, dans la bibliothèque (sous-sol).

Ces mêmes
anées, il
enseigne au Collège de France; il fait aussi partie de
l'Assemblée Constituante en 1848!. Ne désertant
jamais le
terrain du concret, il préside de 1851 à 1858 la
"Classe
des Machines & Outils" aux Expositions
Universelles de Londres et
Paris. Il est d'ailleurs chargé d'un rapport sur ces
machines,
et de "
Voyages
d'exploration dans les filatures et tissages de soie, de
lin et de chanvre en France, entrepris pour constater l'état
de
ces branches d'industrie". Tout cela, c'est lui qui nous
l'apprend dans
l'avertissement de la deuxième édition (1865) du
Traité, pour justifier l'écart entre les deux
parutions.
Après avoir décliné un premier
parrainage en 1831:
"En m'exprimant ainsi
sur la fin
d'une longue et pénible carrière sicentifique, la
reconnaissance me fait un devoir sans réserve, ni fausse
modestie, qu'Arago si contraire au développement des
idées géométriques abstraites, avait
bien voulu,
lors de sa visite d'examen à Metz, en 1831, me proposer, au
nom
de mes illustres et honorés maîtres,
Ampère,
Fourier, Lacroix, Legendre, Poinsot et Poisson, à la
candidature
à la place laissée vacante par l'auteur de
la Mécanique céleste,
candidature
extrêmement flatteuse pour l'amour-propre d'un modeste
officier
du Génie, mais que je n'osais ni ne pouvais accepter par
divers
motifs inutiles à expliquer, et qui, à mon refus,
a
été dévolue à M. Libri."
J-V. P , Avertissement
à la seconde Édition du
Traité
il avait
été élu
Membre de l'Académie des Sciences le 17 mars 1834 (section
de mécanique). Il en était le
Président du 11 mai
1840 à la fin de l'année et en 1842.
Décédé le 22/12/1867 à
Paris, il est enterré au Cimetière du
Montparnasse (
27-éme Division , avenue de l'Est,
1-ère ligne).



Le
Mathouriste
remercie Roland Brasseur, qui lui a fourni toutes les indications
utiles pour trouver la sépulture... et s'est
montré plus
malin, ou mieux outillé que lui, pour photographier,
à
travers la grille, la plaque commémorative
complète
à l'intérieur du monument!

 Le
problème...
...et la
solution!
Le
problème...
...et la
solution!
Curieusement, la plaque
indique le 23
Décembre pour date du décès; plusieurs
biographies
donnant le 22. Dans la séance du 23
décembre 1867 de
l’Académie des Sciences,son Président,
Chevreul, "fait
part à l’Académie de la perte
douloureuse
qu’elle vient de faire dans la personne de M. Poncelet,
décédé le 22 Décembre"
.
Un hommage à signaler -peut-être inattendu: celui
de Raoul Dufy dans sa gigantesque fresque,
la
Fée Électricité, peinte
en 1937 et exposée en
permanence au Musée d'Art Moderne de la Ville de Paris:

 Poncelet, en uniforme
d'officier
Poncelet, en uniforme
d'officier
Mais après tout, même s'il était plus
porté
sur la Mécanique que sur l'Électricité
quand il
s'occupait d'autre chose que de Mathématiques, il ne
faudrait
pas oublier que son modèle de turbine a
équipé
jadis des centrales hydro-électriques, telle celle des
Vernes
(Livet et Gavet, Isère), classée monument
historique. Or,
c'est bien parmi ceux qui ont travaillé aux applications et
à l'industrialisation, à droite de l'usine dans
son
tableau, que Dufy l'a installé!
Le
Traité des Propriétés Projectives des
Figures
 Édition de
1822, en ligne à
l'Université Louis Pasteur à
Strasbourg .
Édition de
1822, en ligne à
l'Université Louis Pasteur à
Strasbourg .
Pour vous faire une (petite!)
idée de cet ouvrage fondateur, de ses buts, de ses
méthodes, à travers son introduction et trois
théorèmes choisis, suivez ce lien. ...
et revenez ensuite!
Les
Théorèmes de Pappus, Pascal et de Poncelet, dans
le Traité
des Propriétés Projectives
Splendeurs
et Misères de la
Géométrie Projective
Suiveurs et... petites
querelles
Des
suiveurs, Poncelet en eut surtout... en Allemagne! Au tout
premier rang, on mettra Plücker,
inventeur des
coordonnées
homogènes, mais aussi Steiner
et Von
Staudt. En France,
l'accueil fut plus que réservé, se
réglant sur le
scepticisme d'un Cauchy
qui n'aimait guère tout ce qui ne
venait
pas... de lui-même, et ne réserva pas aux travaux
de
Poncelet un meilleur accueil qu'à ceux d'Abel
ou Galois.
"Le Mémoire
de M. Poncelet
est
précédé d'un discours
préliminaire qui
offre une sorte de résumé de ses recherches sur
la
Géométrie [.../...]. Dans le discours
préliminaire, l'auteur insiste de nouveau sur la
nécessité d'admettre en
Géométrie ce qu'il
appelle le principe de continuité. Nous avons
déjà discuté ce principe, dans un
Rapport fait il y a plusieurs années sur un autre Mémoire de M. Poncelet , et nous
avons reconnu que ce principe n'était, à
proprement
parler, qu'une forte induction qui ne pouvait être
indistinctement appliquée à toutes sortes de
questions de
Géométrie, ni même en
Analyse. Les raisons
que nous avons données pour fonder notre opinion ne sont pas
détruites par les considérations que l'auteur a
développées dans son
Traité
des Propriétés Projectives.
Quoiqu'il en soit, nous
pensons que le Mémoire de M. Poncelet sur
les centres de moyenne harmoniques fournit de nouvelles preuves de la
sagacité de son auteur, dans la recherche des
propriétés des figures et qu'il
mérite, sous ce
titre, l'approbation de l'Académie."
Cauchy, rapporteur d'un
Mémoire à l'Académie des Sciences
(1824)
"[.../...] Ces paroles
sentencieuses, [.../...]
reproduites tant de fois par des esprits
irréfléchis,
vaniteux ou peu bienveillants à mon égard, ont
fait un
véritable tort à ma réputation dans un
certain
monde scientifique. Rapprochées du but exclusivement
géométrique que je me proposais, [.../...]ainsi
que des dissertations algébriques où le
Rapporteur se
montre, comme d'habitude, enclin à établir sa
supériorité sur l'auteur auquel les
réglements
académiques interdisent toute réplique, ces paroles, ces
dissertations, [.../...] prouvent, mieux que je
n'ai pu le faire [.../...], que M. Cauchy ne
possédait qu'imparfaitement le sentiment de la
véritable Géométrie [.../...]
Pour montrer, par un exemple d'autant plus frappant que je ne doute en
aucune façon de la bienveillance de l'auteur, combien M.
Cauchy a fait illusion, même à des savants qui
passent
avec raison pour de très habiles algébristes, je
citerai
l'un de mes confrères déjà
célèbre,
de
l'Académie des Sciences, qui dans un séduisant
article, en apparence très flatteur pour moi, sur
le Traité
des Propriétés Projectives,
[.../...] est venu
néanmoins soutenir les jugements
irréfléchis portés par M.
Cauchy sur la partie philosophique, à mes yeux la plus
importante de cet ouvrage et que cet illustre académicien
n'a
pas comprise ni voulu comprendre en refusant de m'accorder une
heure d'audience avant la rédaction de son rapport de 1820 [.../...]."
Poncelet, Section Supplémentaire
du Traité
(t. II)
Dans
l'indifférence et l'incompréhension
Françaises, une
très notoire exception, Michel Chasles (1793-1880), lui
aussi Polytechnicien: il est entré à
l'École en 1812, au moment même où la
débâcle de la Grande Armée a conduit
Poncelet en
prison
.

Buste de
Chasles (École Polytechnique)
Néanmoins,
leurs rapports ne
sont pas toujours au beau fixe. Certes, Chasles salue Poncelet dans la
préface de son Traité
de Géométrie Supérieure
(1852) et son Discours
d'Inauguration du Cours de Géométrie
Supérieure à la Faculté de Paris
(1846, mis en annexe à son Traité );
mais il tient aussi à s'en démarquer:
"Je me suis
étendu sur les
ouvrages de Monge et de Carnot, parce que je les regarde comme ayant
ranimé en France l'esprit des méthodes
géométriques et inspiré les jeunes
mathématiciens qui bientôt sont entré
dans cette
voie.
À leur tête se présentent MM. Ch. Dupin
et
Poncelet, dont les remarquables travaux attestent cette heureuse
impulsion. [.../...]
La théorie des transversales
est le principe fondamental du Traité
des Propriétés Projectives des Figures
de
M. Poncelet, où l'on trouve, ave une foule de
résultats
du plus haut intérêt, cette méthode
merveilleuse de
la théorie des polaires
, et le mode de
déformation des figures à trois dimensions [.../...];
méthodes qui, en donnant le moyen de créer
à
volonté, d'une manière en quelque sorte
mécanique,
des théorèmes fort divers et pourtant
dérivés d'un seul, forment les sources les plus
fécondes de la Géométrie moderne."
Chasles,
Discours d'Inauguration
"De la sorte, les
démonstrations impliquent les cas où certaines
parties d'une figure [.../...]
deviennent imaginaires, sans qu'on soit obligé d'invoquer le
principe de continuité dont M. Poncelet
a fait un si heureux usage dans son savant Traité
des Propriétés Projectives des Figures, mais qui ne pouvait
répondre aux vues qui m'ont dirigé dans la
méthode
suivant laquelle je traite la Géométrie."
Chasles, préface au
Traité de
Géométrie Supérieure
Quant à Poncelet, s'il se met, nous l'avons vu, en retrait
derrière ses prédécesseurs, il le fait
sans doute
avec une fausse humilité, n'attendant... qu'un traitement
similaire à son égard de la part des autres, et
protestant à coups de vigoureuses réclamations
quand le
piédestal sur lequel il compte ne lui est pas servi!
"En citant à
plusieurs reprises, dans l'introduction du Traité
des Propriétés Projectives des Figures (t. I
er),
avec
les noms de Desargues, Pascal, de Monge, Livet, Dupin, Brianchon,
Servois ou autres, le nom de M. Chasles comme étant celui de
l'un des précurseurs des méthodes de projection,
de
transformation des figure; en négligeant maladroitement d'y
faire valoir mes propres inventions, je ne m'attendais
guère,
après quatorze années d'un silence regrettable [.../...] que M. Chasles
viendrait prendre pied sur mon propre terrain [.../...]
[.../...] mais, quoique M.
Chasles mentionne mes derniers écrits et se serve
même
avec habileté de la théorie des polaires
réciproques et des centres d'homologie, il ne
s'aperçoit
pas encore que les sécantes communes [.../...] peuvent passer tout
entières à l'infini. [.../...] Évidemment
M. Chasles avait horreur de l'infini ou n'osait pas encore s'y fier,
tout en se perdant dans une série de corollaires
censés
jusque là inconnus. [.../...]
En présentant ses divers Mémoires à
l'Académie de Bruxelles et non à celle de Paris,
M.
Chasles s'évitait l'ennui de discussions
scientifiques,
répendait promptement à l'étranger, en
Angleterre
et en Belgique surtout, et cela au détriment de ses
concurrents,
ses propres travaux, et obtenait d'un seul coup, en 1830, le titre de lauréat
et de membre
de la jeune Académie
de Bruxelles, alors dirigée pr M. Quételet."
Poncelet,
Section Supplémentaire
du
Traité
(t. II)
Heureusement, il y a ce
bon M.
Eiffel et sa tour pour réconcilier Poncelet et Chasles... en
les
faisant figurer sur la même face. Qui n'est pas
-heureusement!-
celle où il a fait inscrire Cauchy!

Cette
Section
Supplémentaire est
truffée de telles controverses de priorité avec
ceux qui,
peu ou prou, touchèrent au même sujet à
la
même époque.
Plücker,
pas mieux loti, doit aussi se justifier:
"M. le docteur
Plücker a donné, t. XVII, p. 37 et 69 des Annales,
divers problèmes et théorèmes sur les
contacts des sections coniques
fort intéressants en eux-mêmes, mais dont, ce me
semble, il aurait dû
citer plus scrupuleusement
les auteurs: par exemple, le théorème
cité au bas de la page 71 et la
construction qui en dérive pour le cercle osculateur des
sections
coniques, sont, si je ne me trompe, bien les mêmes que le théorème
du n° 336, p180 du Traité
des Propriétés Projectives des Figures
, et que la solution
donnée au n° 405, p. 224 et 225 de
cet ouvrage; le théorème
du n° 404, dont elle a été
déduite, est
même plus généra que celui de M. Plücker [.../...] "
Poncelet, lettre aux Annales de Gergonne, 1826
"C'est
d'une lettre de Berlin que j'ai appris, il y a trois ou quatre mois,
avoir été l'objet des injustes attaques
de M. Poncelet. Je n'ai pu y
répondre parce que je n'avais aucune connaissance du fait. M. Poncelet,
infatigable à reproduire toujours les mêmes
accusations contre moi, se
présente de nouveau pour donner les preuves de ce qu'il
avance.[.../...]
J'ai
reconnu dès le premier moment (en parcourant les Annales
) l'importance des travaux de M. Poncelet.
Je m'en suis prononcé dans la préface du premier
volume, et si, après
cela, je n'ai pas consulté son traité, c'est
uniquement parce que je ne
pouvais me le procurer sur le champ, et parce que le titre de mon
ouvrage me permettait de le faire plus tard."
Plücker,
lettre au Bulletin des
Sciences de Férussac, 1828
Le plus amusant -si l'on prend le parti d'en rire- est que ce
même Poncelet cite ce même Plücker en exemple
d'honnêteté intellectuelle quand il s'agit de s'en
prendre... à Steiner!
"[.../...]
quant au livre de Jacob Steiner, dis-je, il est aisé
d'apercevoir par l'introduction et dès les
premières
pages du texte que, laissant entièrement de
côté le
Traité
des Propriétés Projectives des Figures
, mes Mémoires de
1824, et même de 1831, dès lors
imprimés dans le Journal de Crelle
, l'auteur n'entendait nullement
tenir compte du bienveillant avis du Dr Crelle
et des graves repoches de son antagoniste M. Plücker
, mieux éclairé, plus équitable alors
envers ces
mêmes écrits. Le mutisme, le mauvais
vouloir de M.
Steiner sont ici, en effet, poussés jusqu'au point de placer
le
principe de dualité avant celui de la réciprocité
polaire [.../...]"
Poncelet, 1865
Fallait-il le rappeler, les grands hommes sont aussi... des hommes!
Avec leurs mesquineries, leurs sensibiltés à
fleur de
peau; et la victime bien réelle n'est jamais loin de tomber
dans
la névrose obsessionnelle d'un complexe de
persécution...
L'Oubli, le Renouveau
Les publications de Von Staudt (1847, 1856, 1860) marquent la fin de la
période prolifique de la Géométrie
Projective. Selon Coolidge, les cinquante années qui
suivirent virent une grande activité, mais plus dans la
déduction de nouvelles applications que de nouvelles
méthodes, et le sujet n'intéressa plus les
chercheurs, même si les coordonnées
homogènes n'ont cessé d'être
employées en Géométrie
Algébrique.
Signe de désaffection certain, les Espaces Projectifs
disparurent des programmes de Mathématiques
Supérieures et Spéciales en 1974.
Pourtant,
la fin du XXème
siècle a connu une spectaculaire réactivation des
concepts projectifs et des coordonnées
homogènes, à la fois en
"Mathématiques
Pures" et en "Mathématiques Appliquées". (Les " "
ne sont là que pour souligner le caractère
stupide de cette ultime forme de ségrégation...)
Le premier grand courant
est lié à l'étude des
courbes
elliptiques, dont les espaces projectifs restent
l'indispensable toile de fond, et qui sont au cœur de trois
résultats récents et... essentiels:
Le
second concerne les applications des
Mathématiques à la CAO et à
l'Infographie:
- Courbes
Rationnelles: Depuis les années 1980,
les courbes de Bézier se sont imposées dans la
CAO, puis toutes les applications de l'informatique. Ce sont, on le
sait, des courbes polynômiales par morceaux, et les ennuis
commencent dès qu'on veut représenter un
"bête" cercle: il faudra raccorder de nombreux morceaux! Or
un cercle est paramétrable rationnellement; par exemple,
dans le cas où le centre est O et le rayon 1:
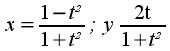
Pour retrouver des
polynômes, il suffit... de passer aux coordonnées
homogènes de
la Géométrie Projective,
puisqu'en posant
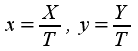
on parvient au
paramétrage, cette fois polynomial
qui ramène
dans le monde des représentations de Bézier.
- Photogrammétrie
: cette technique de reconstitution
de volumes à partir de deux photographies planes,
si elle a été envisagée dès
1849 (historique ici), connait
aujourd'hui de spectaculaires
développements
grâce à l'apport de l'informatique. Qui fait une photo... fait
de la Géométrie
Projective sans le savoir, puisque cela envoie les points de l'espace
sur un plan (celui du film, ou, désormais, des capteurs CCD)
par une projection centrale (le centre focal de l'objectif). Un vrai
retour aux sources et à Poncelet! Alors, vous pensez, si
l'on en fait deux...
Mais soyons sérieux: les formules "consomment"
énormément de coordonnées
homogènes et transformations projectives; et les cours
spécialisés commencent par une initiation
géométrique des étudiants. On enseigne
donc désormais la Géométrie
Projective à des étudiants en Architecture, en
Sciences Géographiques: bien malin qui l'aurait dit il y a
vingt ans! (voir cet exemple de cours de Géométrie
Projective appliquée à l'Analyse des Images)
Quant à son
utilité, nous n'en donnerons qu'un exemple
emblématique: l'Institut de Géodésie
et Photogrammétrie de l'
ETH
de
Zürich l'a
employée
avec succès pour fournir toutes les données
permettant de reconstruire à l'identique les fameux Bouddhas
de Bamiyan (Afghanistan), dynamités en 2001 par
les talibans! Des maquettes en 3D ont été
réalisées pour attester ce que les calculs
pouvaient faire. Il n'y manque plus que la volonté politique
et financière; mais la
Géométrie
Projective aura, quant à elle, fait tout ce qui
était en son pouvoir pour que ce crime échoue
dans son intention fanatique: faire disparaître ces
merveilles de la vue et de la mémoire des hommes.

 ?
?
 aujourd'hui
demain?
aujourd'hui
demain?
Images de reconstructions virtuelles (y compris la vallée)
empruntées
au siteThe Bamiyan
Project : visitez-le!
Références
Introduction
à la Géométrie Projective
Application
à la Géométrie Algébrique
et aux Courbes Elliptiques
- Y. HELLEGOUARCH, Invitation
aux Mathématiques de Fermat-Wiles (Dunod)
- A. KNAPP, Elliptic
Curves
(Princeton University Press)
- M. REID, Undergraduate
Geometry (Londo Mathematical Society, n°12)
- J. SILVERMAN, J.TATE, Rational
Points on Elliptic Curves (Springer-Verlag)
Application
aux Courbes Rationnelles
- J.-C. FIOROT, P.JEANNIN, Courbes et Surfaces Rationnelles
(Masson)
Application
à la Photogrammétrie, à l'Analyse
d'Images et à la Vision par Ordinateur
Tout d'abord, signalons un
article
introductif particulièrement accessible et
motivant, que les auteurs ont eu la gentillesse
de mettre à la disposition des étudiants sous
forme de fichier téléchargeable; qu'ils en soient
ici remerciés!
R.MOHR, M.DOUZE, P. STURM:
Géométrie
Projective, Analyse Numérique et Vision par Ordinateur
, Bulletin de l'UPS (Union des Professeurs de Spéciales)
n°219, Juillet 2007.
Pour continuer, queques autres références
à télécharger:
Dédicace
in Mémoriam
Le
Mathouriste
dédie
cette page à la mémoire de son
vénéré professeur de
Spéciales, grand
amateur de Géométrie (en
général) et de
Projective (en particulier).
Comment pourrait-il oublier cette incroyable prophétie,
formulée comme une triste confidence en 1972, alors qu'on ne
pouvait deviner les applications récentes qu'il vient
d'évoquer :
"Les
coniques et la projective vont disparaître des programmes...
Mais vous verrez, elles reviendront!"

Gilbert
Péronny (1923-1996)
en cliquant sur l'image, vous irez à une page
complémentaire de souvenirs.



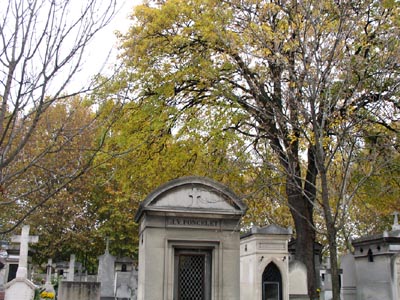




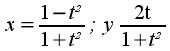
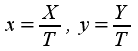

 ?
?

