Ce
qui fut fait... sans même inscrire la localisation sur ses notes
de correction, sûr de sa mémoire; elle fonctionna
parfaitement pour l'y guider dans les jours qui suivirent, interroger
la pierre aussi pieusement que Claude Nougaro questionnant la maison de
Jacques Audiberti... Mais 30 ans plus tard, c'était plus
critique: où pouvait
bien se trouver ce fichu monument?
Du Bac au ... backstage!
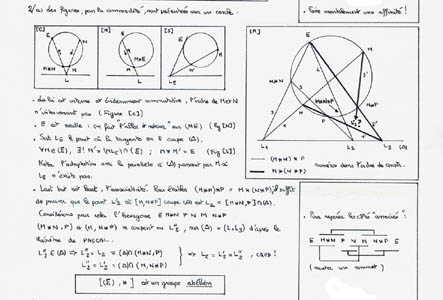
Le
sujet du Capes Interne 1991 reprend loi de groupe et
théorème de Pascal, mais, en quelque sorte, il inverse le
point de vue (question d'époque, sans doute...). On prouve le
théorème géométrique d'abord, on en
déduit l'associativité : la Géométrie
prouve l'Algèbre, cette fois!
Passé de l'autre côté... de l'estrade et de la
craie, l'ancien hypotaupin s'est appliqué un peu plus pour faire
sa figure, cette fois! Mais il est vrai qu'il n'opérait plus en
temps limité... voici donc un extrait du corrigé proposé à ses étudiants.
 |
 |
loi de groupe: preuve complète
|
zoom sur l'associativité
|
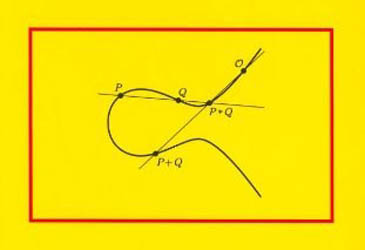
Mais d'où sort cette mystérieuse loi de groupe?
Tout s'éclaire si l'on regarde la réunion du cercle et de la droite comme un
cas particulier de courbe cubique. L'équation de la réunion est de la forme (repère ua centre du cercle)
| ( x² + y² - R² ) . ( a x + b y +c ) = 0 |
ce qui, développé, est une équation du troisème degré.
Or, il y a une loi de groupe sur une cubique (qu'on note, d'usage, additivement), dont
l'associativité consiste... en un magnifique
théorème d'alignement!
|
|
 |
| cercle et droite, dans la copie |
cubique propre, en couverture d'un excellent ouvrage |
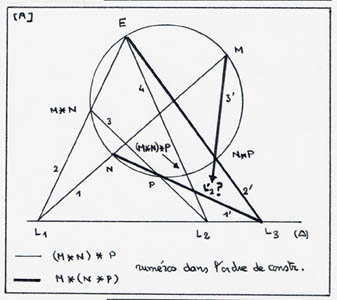
La comparaison entre les deux cas ne nécessite qu'un petit dictionnaire entre les notations des deux figures, que voici
| Copie
|
B |
C |
a |
O |
B * C |
| Livre |
P |
Q |
P * Q |
I |
P + Q |
On constate qu'il s'agit bien de la même construction!
Petit Commentaire : (auquel l'auteur de ces lignes ne peut résister...)
Dans
les années 1970-80, beaucoup qualifiaient ce genre de résultats de
résultats démodés, sans intérêt. Ce à quoi les années qui suivirent
infligèrent un sérieux démenti: factorisation elliptique (Lenstra,
1985), indépendance algébrique de π et exp (π)
(Nesterenko, Philippon, 1995) et... preuve du Grand Théorème de Fermat
(Wiles, 1994-95) utilisent cette fameuse loi de groupe, et une bonne dose
de Géométrie Projective, c'est dire... exactement la manière de passer
du cercle à une conique quelconque, l'esprit même de Desargues et
Pascal!
S'il restait à
illustrer la difficulté de lire l'avenir avec clairvoyance,
voilà de quoi le faire, et de belle manière...
|
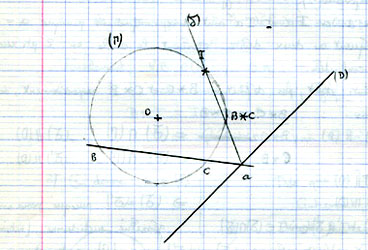
Preuve n°2 : sur le cercle, avec le théorème de
Ménélaüs (corrigé du devoir)... comme Pascal?
"Je vous parle d'un temps que les moins de vingt ans ne peuvent pas connaître..."
En ce temps-là, pas de corrigé photocopié et
distribué par le professeur! Celui-ci fait une correction "au
tableau", et l'élève note... comme il peut! Ce n'est en
aucun cas une excuse, mais une simple explication au caractère
peu soigné des deux pages de notes ci-dessous, que le souci de
l'ambiance d'époque nous pousse à laisser telles quelles:
la figure "tombe" plus ou moins bien, le point K de la figure de droite
s'envole trop loin et irait s'immiscer dans celle de gauche,
raté pour obtenir un bel alignement!
Faut-il rappeler que pour faire une belle figure, bien
disposée... il faut souvent en avoir préalablement
raté au moins une, souvent plusieurs?
C'est la preuve la plus élémentaire qu'on puisse
donner, et la plus probablement utilisée par Pascal. En
effet, elle ne nécessite que l'emploi du théorème
de
Ménélaüs (
démonstration interactive
ici), parfaitement en sa possession. Dans les années 1960-70,
c'était un résultat que devait connaître, et savoir
exploiter, un élève de Terminale C.
Et, suggère l'énonce de Capes 1991, notre bachelier doit
pouvoir en déduire le théorème de Pascal sur
l'ellipse, comme sur le monument de Gournier. Il suffit de
considérer l'ellipse comme affine de son cercle principal; cette
transformation conserve les alignements et concours, puisque l'image
afine d'une droite est une droite.
Preuve n°3 : un parfum de Géométrie Projective
On l'a dit en préambule: disposant de la preuve dans le cas
particulier du cercle, Pascal n'a plus qu'à appliquer les
idées de Desargues (
principe détaillé à cet endroit de notre page Desargues ) .
Mais on peut faire mieux dans le genre, en
partant d'une situation encore plus particulière, mais suffisante pour engendrer toutes les situations par projection conique. Nous empruntons à J. GRAY,
Worlds Out of Nothing: A Course in the History of Geometry in the 19th Century
(Springer-Verlag) la preuve suivante, qui nécessite, en
contrepartie de son extrême simplicité, de connaître
quelques rudiments de Géométrie Projective :
On suppose de plus que la droite
est la droite de l'infini (ensemble de toutes les directions du plan ,
T = 0 en coordonnées homogènes). Dire que deux droites
AC' et
A'C se coupent en
Q sur la droite de l'infini, c'st dire qu'elles sotnt parallèles; de même
AB' et
A'B en
R. Le théorème de Pascal pour cet hexagramme particulier dit que
BC' et
B'C se coupent en
P aligné avec
Q et
R , c'est à dire sur la droite de l'infini: il s'agit donc d'établir que
BC' et
B'C sont
parallèles, et c'est un jeu très simple à l'aide
des angles alternes-internes et de l'égalité des angles
interceptant un même arc de cercle.
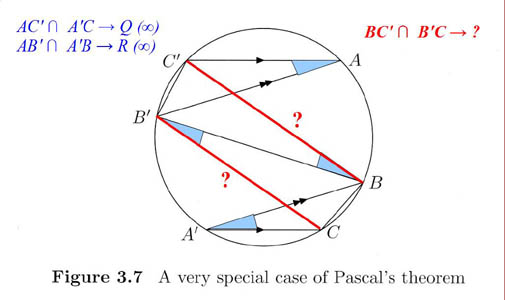Une version "colorisée" de la figure du livre de J. Gray
On peut montrer que tout couple
(conique, droite) peut être projectivement envoyé sur le
tout couple (conique, droite de l'infini), ce qui achève la
preuve (nous ne détaillons pas ce point technique)
Preuve n°4 : une fragrance de Géométrie Algébrique
[voir par exemple J. SILVERMAN, J.TATE,
Rational
Points on Elliptic Curves (Springer-Verlag), évoqué plus haut]
Tout repose sur le
Lemme :
Soient deux cubiques (C1) et (C2) ayant 9 points d'intersection. Alors, toute cubique (Γ) passant par 8 de ces points passe par le neuvième. |
Preuve du Lemme :
(Γ) a
une équation de la forme (selon le système de
coordonnées, cartésiennes usuelles ou homogènes):
| Cartésiennes
|
f (x, y) = a x3 + b x2 y + c x y2 + d y3 + e x2+ f x y +g y2+ h x+i y + j = 0 |
| Homogènes |
F (X, Y, T) = a X3 + b X2 Y + c XY2 + d Y3 + e X2T + f XYT +g Y2T + h XT2 + i YT2 + j T3 = 0 |
Les cubiques passant par 8 points distincts sont donc déterminées par un système linéaire de 8 équations à 10 inconnues: a, b, ... j. Ce
système est de rang 8 pour des points d'intersection deux
à deux distincts (point technique sans difficulté, mais
dont nous omettons les détails), et par suite admet un espace de
dimension 2 de solutions, dont on peut prendre pour base les
sysstèmes correspondant à (C1) et (C2) . (Γ) a donc une équation de la forme
F (X, Y, T) = λ F1 (X, Y, T) + μ F2 (X, Y, T) = 0
d'où le passage par le neuvième point pour qui, comme pour les 8 premiers, F1 (X, Y, T) = F2 (X, Y, T) = 0.
CQFD .
Preuve du Théorème :
En préalable, observons que, de façon similaire à
la réunion d'une droite et une conique vu plus haut, la
réunion de trois droites définit une cubique, comme on le
constate en développant le produit
( u1 X + v1 Y + w1 T ) . ( u2 X + v2 Y + w2 T ) . ( u3 X + v3 Y + w3 T ) = 0
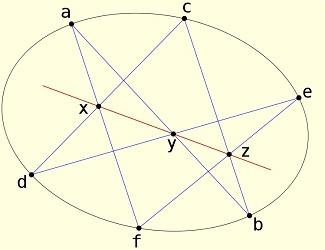
On considère les deux cubiques formée chacune de la réunion de 3 droites:
∪
(cd) ∪
(ef) et
(C2) = (bc) ∪
(de) ∪
(fa) .
Que leur intersection soit composée de 9 points est
élémentaire (à condition d'adoptet le point de vue
projectif pour lequel deux droites distinctes se coupent toujours,
fût-ce à l'infini, en un point unique), car chaque droite
rencontre la cubique "adverse" en 3 points (3 intersection
droite-droite). Ce sont a,
b,
c, d ,
e,
f bien sûr, mais aussi
x,
y,
z dont l'alignement est à prouver.
Soit
(Γ) la cubique réunion de la conique donnée et de la droite (xy) . Elle a 8 points en commun avec chacune des cubiques
(C1) et
(C2) , donc passe par le neuvième, c'est à dire z. Et comme z ne peut être sur la conique (car alors, la droite (bc) la couperait en trois points b, z, c , soit un de plus que ne le permet le degré) , il est sur la droite (xy) .
