Vous trouverez
le
texte complet présenté
et analysé sur le site
BibNum
.
Mais voici qu'en 2011, l'auteur de cette présentation doit
avouer sa perplexité :
"Seulement, le titre est une
chose, le texte en est une autre. L’amphigouri qui fait le
charme du premier disparaît totalement du second. On n'y
trouve plus que de la géométrie et, qui plus est,
rédigée de façon sèche.
[...]Or je n'ai pas grand goût pour la
géométrie (j’étais
spécialisé en théorie des nombres). Du
coup, essayer de décrypter le texte m'intéresse
peu. Somme toute, le titre m'a entraîné sur une
fausse piste. Je m'attendais à une langue plaisante parce
que fleurie, je tombe sur des coups de trique !
Parcourant néanmoins le Brouillon Projet, je me suis senti comme Fabrice
à Waterloo. Si les professeurs, les
encyclopédies, les dictionnaires, ne
répétaient pas à l'envi qu'il est
fondateur, je ne m'en serais jamais rendu compte. C'est que, pour
estimer l'apport de Desargues et évaluer son influence, il
faut connaître bien l'état de la
géométrie avant lui et l'état
après lui, puis les comparer. Une telle entreprise exige une
érudition qu’on n’atteint
guère que si on est historien professionnel des
mathématiques. "
Vous voilà prévenus: si vous vous
confrontez au texte brut, ne vous étonnez pas si vous vous
senez en difficulté. Le père de la
Géométrie Projective, Poncelet, rappelle
l'incompréhension quasi générale en
son temps:
"DESARGUES,
qu'on peut appeler, à plus d'un titre, le MONGE
de son siécle, que les biographes n'ont point assez connu,
ni
assez compris; DESARGUES , enfin, que des contemporains,
indignes du
beau titre de géomètre, ont noirci,
persécuté
et dégoûté, pour n'avoir pu se mettre
á la
hauteur de ses idées et de son génie, fut, je
crois, le
premier, d'entre les modernes qui envisagea la
Géométrie
sous le point de vue général que je viens de
faire
connaitre. "
Seuls Pascal et
Fermat saluent l'ouvrage:
"Nous
démontrerons aussi (fig.1) la
propriété suivante, dont le premier inventeur est
M. Desargues, Lyonnois, un des grands esprits de ce temps, et des plus
versés aux mathématiques, et entre autres aux
coniques, dont les écrits sur cette matière,
quoiqu'en petit nombre, en ont donné un ample
témoignage à ceux qui auront voulu en recevoir
l'intelligence. "
"J'estime beaucoup M. Desargues
et d'autant plus qu'il est lui seul inventeur de ses coniques. Son
livret qui passe, dites vous, pour jargon m'a paru très
intelligible et très ingénieux. "
Fermat, lettre
à Mersenne
Quelques liens complémentaires
Un Théorème de Desargues...
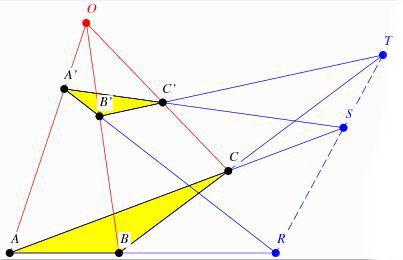
Voici un exemple à la fois simple et typique. Ce
théorème stipule ceci (Fig 1):
Soient dans un plan,
les triangles ABC
et A'B'C',
tels que AA', BB' et CC'
concourent en O.
Alors, les points R = AB ∩ A'B', S= AC ∩ A'C',
T= ABC ∩ B'C', sont alignés. |
Si l'on sait former
des équations de droites, on peut le vérifier par
des calculs idiots (et pénibles). On l'aura
prouvé,
certes... mais on n'y aura rien
compris;
et de toutes façons, on n'aurait pas pu le
découvrir: il faut que quelqu'un (qui, lui, sait le
résultat) nous dise:
"Démontrez que"....
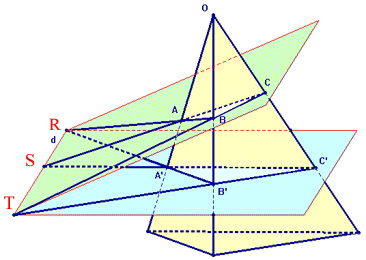
Si, au contraire, on réalise que ce n'est que la projection
d'une configuration de l'espace où les triangles sont dans
deux plans sécants,
R,
S, T se trouvent nécessairement sur la droite
d'intersection... et tout s'éclaire! (Fig 2)
|
|
|
| Fig 1:
Théorème de Desargues, dans le plan |
Fig 2: Quand tout s'explique...
par l'espace! |
|
- Pour voir une introduction douce à la
Géométrie Projective, inclaunt le
théorème de Desargues (en Anglais):
 Video de N.J Wildberger
(cliquer sur l'image)
Video de N.J Wildberger
(cliquer sur l'image)
... et ce qu'a pu en faire Pascal
Dans cette
projection centrale de centre O,
nom savant pour ce qui est le principe de la Perspective en art et...
celui de l'appareil photo (O est l'oeil, ou le centre optique du
système de lentilles,
A'B'C' le
plan du sujet,
ABC
celui du film ou du capteur), les alignements se conservent,
les droites se transforment en droites... et tout
théorème parlant de concours ou d'alignement dans
un plan "source" sera vrai dans le plan "image".
Maintenant, imaginons qu'
on remplace
les triangles de l'espace par diverses sections d'un cône:
c'est appliquer la défintion même des coniques,
selon
Apollonius
de Pergé.
On peut faire l'expérience suivante:
matérialisons un cône de révolution par
le cône de lumière issu d'un abat-jour,
posé sur une table horizontale. La section par le plan
vertical du mur est une magnifique hyperbole...
 un
Mathouriste
trouve
ça facilement dans sa chambre d'hôtel!
un
Mathouriste
trouve
ça facilement dans sa chambre d'hôtel!
Il n'y aurait plus
qu'à prendre un papier calque, y dessiner le
théorème de Pascal sur un cercle de
même diamètre que l'abat jour... au mur se
trouverait projeté le théorème de
Pascal sur l'hyperbole, tandis qu'au plafond, on le verrait encore sur
le cercle...
NB: en fait, les deux branches de l'hyperbole étant
utilisées; il faudrait un abat-jour cylindrique, la source
lumineuse rigoureusement à mi-hauteur. Sur note image, on
voit bien que haut et bas appartiennent à des hyperboles
différentes.
C'est ce principe qu'applique Pascal, en lecteur avisé de
Desargues, que reprendra
Poncelet en 1813, et c'est
pourquoi Desargues apparait bien comme le
précurseur
de la Géométrie Projective.