LAMBERT à Mulhouse
Souvenirs
Johann-Heinrich Lambert (1728-1777) est né à Mulhouse, pendant l'époque où cette ville était Suisse (1515-1798); il y a vécu toute sa jeunesse, jusqu'à 18 ans, dans une maison encore visible aujourd'hui, place... Lambert, dans le prolongement de la rue Lambert. Le Mathouriste est heureux de vous proposer quelques clichés dûs à son amie Janine Taillé, Mulhousienne d'origine...

Maison Natale de Lambert (source inconnue)
Par rapport à
cette photo,
hors cadre sur la droite, se trouve la colonne Lambert,
érigée en 1828 pour commémorer le
centenaire de sa
naissance. Célébrant avant tout l'astronome, elle
porte
une analemme et elle est surmontée d'un globe...
céleste,
ce qui rend savoureuse l'enseigne commerciale à
l'arrière-plan!



Base de la colonne: détail des inscriptions.


Échantillon des impresions:
"On m'a, pour ainsi dire, presque forcé de prendre la plus maussade créature qui soit dans l'univers pour la mettre dans notre Académie. Il se nomme Lambert, et, quoique, je puisse attester qu'il n'a pas le sens commun, on prétend que c'est un des plus grands géo- mètres de l'Europe. Mais, comme cet homme ignore les langues des mortels et qu'il ne parle qu'équations et Algèbre, je ne me propose pas de sitôt d'avoir l'honneur de m'cntretenir avec lui. En revanche, je suis très-content de M. Toussaint, dont j'ai fait l'acquisition. Sa science est plus humaine que celle de l'autre. Toussaint est un habitant d'Athènes, et Lambert un Caraïbe ou quelque sauvage des côtes de la Cafrerie. Cependant, jusqu'à M. Euler, toute l'Académie est à genoux devant lui, et cet animal, tout crotté du bourbier de la plus crasse pédanterie, reçoit ces hommages comme Caligula recueillait ceux du peuple romain, chez lequel il voulait passer pour dieu. Je vous prie que ces petites anecdotes de notre Académie ne sortent pas de vos mains."
"M. Lambert, sur qui vous souhaitez de savoir mon sentiment, est sans contredit un des meilleurs sujets de notre Académie ; il est très-laborieux et soutient presque seul notre Classe de Physique. Il possède assez bien l'Analyse, mais son fort est la Physique [...]. Au reste, il a quelque chose de singulier dans son maintien et dans sa conversation qui déplaît au premier abord, et je ne suis pas surpris que le roi ne l'ait pas goûté, ayant eu moi-même de la peine à m'accommoder à ses manières. Il était ou du moins il me parut si plein de lui-même, lorsque j'arrivai ici, que je pris le parti de ne pas le fréquenter, mais en même temps de ne laisser échapper aucune occasion de le rabaisser; cela l'a rendu beaucoup plus traitable, et à présent nous sommes assez bons amis."


Théorie...et pratique, par J.-H. Lambert


Début de l'article de Lambert, montage de l'article d'Euler.

Traduisons ce résultat en langage familier: π n'est pas le quotient de deux entiers. π n'est pas égal à 3,14 (car ce serait la fraction 314/100), pas plus qu'il n'est égal à 22/7 (célèbre valeur approchée dans les écoles primaires de jadis...), ni davantatge à 355/113 (approximation de Metius). On avait beau s'en douter depuis l'Antiquité (et les Grecs avaient su prouver l'irrationalité d'autres nombres, tels que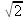 , diagonale du carré de côté 1), il a
fallu attendre jusque là pour en apporter la preuve
irréfutable... à telle enseigne que Lambert prend
des précautions vis à vis de son lecteur!
, diagonale du carré de côté 1), il a
fallu attendre jusque là pour en apporter la preuve
irréfutable... à telle enseigne que Lambert prend
des précautions vis à vis de son lecteur!
Il y a plus: la fondation d'une nouvelle théorie arithmétique, celle de la Transcendance. Après avoir étendu la preuve d'irrationalité de e donnée par Euler (1737) à celle de toutes ses puissances, Lambert, qui emploie pour la première fois ce mot, formule la conjoncture de la transcendance de e: non seulement ses puissances sont irrationnelles, mais encore aucune combinaison entière de celles-ci ne peut être annulée.

Le moment fatidique, où Lambert parle pour la première fois de transcendance, empruntant le mot à Leibniz.
Celui qui prouvera le résultat, Hermite, en 1873 (voir notre page Hermite
pour plus de détails), ne cessera de rendre hommage
à celui qui a montré la voie:

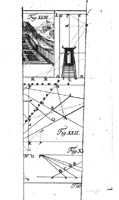
La pièce maîtresse: le développement en fraction continue de la fonction tan x
En haut de la page 277 (à droite), le calcul des réduites lui fournit... des approximants de Padé!
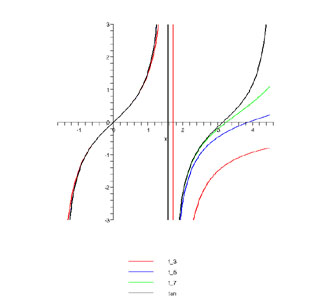
la fonction tan x et ses premiers approximants:
une convergence bien meilleure que celle de la série entière!
Enfin, au passage, Lambert y définit ce que nous appelons
aujourd'hui les fonctions
hyperboliques, en justifiant, figure
à l'appui, que l'on parle d'une trigonométrie
hyperbolique.
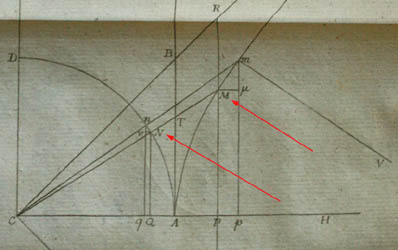
Le cercle x²+ y² = 1, l'hyperbole x²- y² =1 , et les projections associées: illustration (hors texte) de son article
Après cette brève présentation, vous brûlez sûrement d'en savoir plus! Or, le texte intégral commenté du mémoire de Lambert est accessible en ligne:
le texte de Lambert sur l’irrationalité de π (1761) sur le site BibNum .
à télécharger en complément, pour replacer le travail de Lambert dans la continuité historique :
Alain Juhel: Irrationalité et Transcendance: État des Lieux avant Hermite , conférence aux journées Padé (Lycée Faidherbe, Lille, 1994).
Et pour prolonger, avec toutes les preuves ultérieures de l'irrationnalité de π :
Denis Roegel, Lambert’s proof of the irrationality of Pi: Context and translation (2020)
Base de la colonne: détail des inscriptions.
En matière
d'urbanisme...
faire et défaire, c'est toujours travailler. C'est ainsi que
la
colonne, érigée près de la maison de
Lambert, fut
déplacée rue de Belfort, puis vint retrouver sa
localisation d'origine.


D'autres photos... un peu plus
ensoleillées, provenant d'un site sur les cadrans solaires,
très riche en images.


Liens biographiques
- Biographie à l'Université Saint-Andrews
- Biographie sur Wikipedia
- sur
le site de l'AMUSS (Physiciens en Almsace)
Quelques motifs de célébrité.
Autodidacte (obligé d'arrêter ses études à 12 ans pour aider son père, tailleur), Lambert était assez conscient de sa valeur : tant Lagrange que Frédéric II de Prusse l'avaient remarqué dès son arrivée à Berlin (1764). Mais il y avait de quoi, car son génie s'est appliqué avec succès à une grande variété de domaines.Échantillon des impresions:
"On m'a, pour ainsi dire, presque forcé de prendre la plus maussade créature qui soit dans l'univers pour la mettre dans notre Académie. Il se nomme Lambert, et, quoique, je puisse attester qu'il n'a pas le sens commun, on prétend que c'est un des plus grands géo- mètres de l'Europe. Mais, comme cet homme ignore les langues des mortels et qu'il ne parle qu'équations et Algèbre, je ne me propose pas de sitôt d'avoir l'honneur de m'cntretenir avec lui. En revanche, je suis très-content de M. Toussaint, dont j'ai fait l'acquisition. Sa science est plus humaine que celle de l'autre. Toussaint est un habitant d'Athènes, et Lambert un Caraïbe ou quelque sauvage des côtes de la Cafrerie. Cependant, jusqu'à M. Euler, toute l'Académie est à genoux devant lui, et cet animal, tout crotté du bourbier de la plus crasse pédanterie, reçoit ces hommages comme Caligula recueillait ceux du peuple romain, chez lequel il voulait passer pour dieu. Je vous prie que ces petites anecdotes de notre Académie ne sortent pas de vos mains."
Frédéric
II à d'Alembert
"M. Lambert, sur qui vous souhaitez de savoir mon sentiment, est sans contredit un des meilleurs sujets de notre Académie ; il est très-laborieux et soutient presque seul notre Classe de Physique. Il possède assez bien l'Analyse, mais son fort est la Physique [...]. Au reste, il a quelque chose de singulier dans son maintien et dans sa conversation qui déplaît au premier abord, et je ne suis pas surpris que le roi ne l'ait pas goûté, ayant eu moi-même de la peine à m'accommoder à ses manières. Il était ou du moins il me parut si plein de lui-même, lorsque j'arrivai ici, que je pris le parti de ne pas le fréquenter, mais en même temps de ne laisser échapper aucune occasion de le rabaisser; cela l'a rendu beaucoup plus traitable, et à présent nous sommes assez bons amis."
Lagrange à
d'Alembert
Œuvres...
- en Astronomie, on luit doit une méthode de calcul pour les orbites des comètes: texte explicatif n°1, texte explicatif n°2. (voir également H. DÖRRIE, 100 Great Problems of Elementary Mathematics, Dover - problème 88) . "Le Théorème de Lambert, par sa simplicité et par sa généralité, doit être regardé comme l'une des plus ingénieuses découvertes qui aient été faites dans l'étude du système du monde", écrivait Lagrange.
- en Cartographie, sa méthode de projection conforme conique (dite Projection Lambert) est toujours appliquée; de1948 à 2000, la France était découpée en 4 zones, chacune cartographiée avec une projection de ce type. En 2000 un nouveau système de projections, Lambert 93 a été rendu obligatoire par décret (calculs associés).
- en Physique, la loi de Lambert régit empiriquement à l'absorption de lumière selon le milieu traversé; elle est la base du modèle informatiques le plus simple de rendu des surfaces. (voir par exemple cette page)
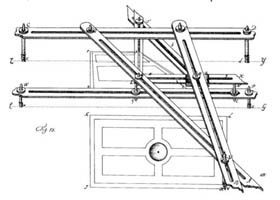
- en Géométrie, il étudie le postulat des parallèles (postulat d'Euclide), et il réalise une étude de la perspective en ne négligeant pas l'aspect pratique , puisqu'il conçoit une machine pour faire la représentation en perspetive des figures, le perspectographe. ( voir aussi un texte avec des figures originales du manuscrit). On pourra aussi cosulter cette étude en deux parties: Perspective, géométrie et esthétique chez Lambert (Partie I, Partie II) sur lesite web: Images des Mathématiques, du CNRS.




Théorie...et pratique, par J.-H. Lambert
- en Analyse, la fonction W de Lambert est l'Arlésienne d'un célèbre article sur les séries (1758), dans lequel il se préoccupe de développer en série entière les racines de certaines équations, algébriques d'abord, puis transcendantes.En effet, W n'y apparaît pas! La résolution de x = f(w) = wew qui définit la fonction W telle que W(x)eW(x) = x, est un exemple pris par Euler dans un article (1783) où il salue, d'entrée de jeu, l'ingéniosité de son compatriote et nomme séries de Lambert de telles séries.


Début de l'article de Lambert, montage de l'article d'Euler.
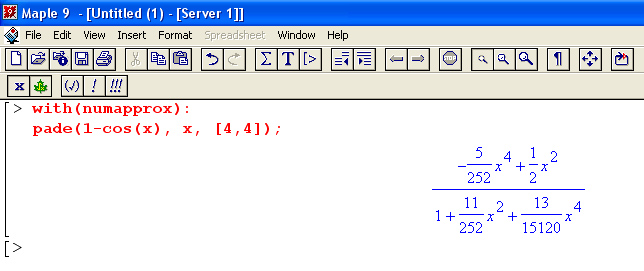
- et l'on trouve dans cet article une autre idée importante: la définition directe (ie, comme fraction rationnelle approchant le mieux la fonction à degrés du numérateur et du dénominateur imposés, des approximants de Padé ! L'exemple 1 - cos x est traité, on pourra comparer le résultat avec un ordre d'une ligne dans un logiciel de calcul formel...


- Œuvres complètes en ligne : index chronologique, index thématique .
- Un article sur le site de Culture Maths : Jean-Henri Lambert (1728-1777): les 15 problèmes de géométrie de la règle .
- Œuvres numérisées à l'Université de Strasbourg
... et Chef-d'-œuvre!
Mais la pièce la plus fascinante de Lambert (du point de vue du Mathouriste) est sans hésitation la preuve d'irrationnalité du nombre π, publiée dans les Mémoires de l'Académie de Berlin (1761).Traduisons ce résultat en langage familier: π n'est pas le quotient de deux entiers. π n'est pas égal à 3,14 (car ce serait la fraction 314/100), pas plus qu'il n'est égal à 22/7 (célèbre valeur approchée dans les écoles primaires de jadis...), ni davantatge à 355/113 (approximation de Metius). On avait beau s'en douter depuis l'Antiquité (et les Grecs avaient su prouver l'irrationalité d'autres nombres, tels que
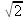 , diagonale du carré de côté 1), il a
fallu attendre jusque là pour en apporter la preuve
irréfutable... à telle enseigne que Lambert prend
des précautions vis à vis de son lecteur!
, diagonale du carré de côté 1), il a
fallu attendre jusque là pour en apporter la preuve
irréfutable... à telle enseigne que Lambert prend
des précautions vis à vis de son lecteur!" Car s'il y fallait une
fraction fort composée, quelle raison y aurait-il, pourquoi
telle plutôt que telle autre? Quelque
vague que soit ce raisonnement, il y a néanmoins des cas
où on ne demande pas davantage. Mais ces cas ne sont pas
ceux de la quadrature du cercle."
Il y a plus: la fondation d'une nouvelle théorie arithmétique, celle de la Transcendance. Après avoir étendu la preuve d'irrationalité de e donnée par Euler (1737) à celle de toutes ses puissances, Lambert, qui emploie pour la première fois ce mot, formule la conjoncture de la transcendance de e: non seulement ses puissances sont irrationnelles, mais encore aucune combinaison entière de celles-ci ne peut être annulée.
| Il n'existe pas de polynôme P à coefficients entiers relatifs tel que P(e) = 0. |
Le moment fatidique, où Lambert parle pour la première fois de transcendance, empruntant le mot à Leibniz.
"Tout ce que je
puis, c'est de refaire ce qu'a déjà fait Lambert,
seulement d'une autre manière..."
Non seulement ce texte occupe une position
charnière dans l'histoire de l'Irrationalité et
de la Transcendance, mais aussi il frappe par sa rigueur impeccable.
Utilisant, comme Euler, le merveilleux outil des fractions continues,
il ne se contente pas de découvrir, il accompagne cette
découverte, dans un deuxième temps, d'une
démonstration d'une rigueur bien supérieure
à celle du magistral prédécesseur,
Euler... et à celle se son "suiveur", Legendre, qui
perfectionnera le résultat pour établir
irrationnalité du nombre π²,
publiée en 1795, en partant d'une série
parachutée sans l'ombre d'une indication sur son
inspiration. La pièce maîtresse: le développement en fraction continue de la fonction tan x
En haut de la page 277 (à droite), le calcul des réduites lui fournit... des approximants de Padé!

la fonction tan x et ses premiers approximants:
une convergence bien meilleure que celle de la série entière!

Le cercle x²+ y² = 1, l'hyperbole x²- y² =1 , et les projections associées: illustration (hors texte) de son article
Après cette brève présentation, vous brûlez sûrement d'en savoir plus! Or, le texte intégral commenté du mémoire de Lambert est accessible en ligne:
le texte de Lambert sur l’irrationalité de π (1761) sur le site BibNum .
à télécharger en complément, pour replacer le travail de Lambert dans la continuité historique :
Alain Juhel: Irrationalité et Transcendance: État des Lieux avant Hermite , conférence aux journées Padé (Lycée Faidherbe, Lille, 1994).
Et pour prolonger, avec toutes les preuves ultérieures de l'irrationnalité de π :
Denis Roegel, Lambert’s proof of the irrationality of Pi: Context and translation (2020)
Revenir
à la Home
Page du
Mathouriste
