Omar KHAYYAM
du Septième Ciel auTroisième Degré ...
#3 : le Traité des Équations Cubiques
 |
 |
| illustration de Dulac pour les Rubáiyáts | copie du traité d'algèbre (source inconnue) |
Ouvrage essentiel? Bien évidemment, car c'est un chaînon longtemps manquant entre Al-Khwarizmi, qu'il prolonge remarquablement, et d'une part les algébristes italiens de la Renaissance, qu'il précède, mais d'autre part -faut-il dire surtout?- Descartes dans l'interaction entre Algèbre et Géométrie.
C'est en effet très tard, en 1851, que cet ouvrage est rendu accessible à des lecteurs occidentaux ne pratiquant pas la langue arabe. Il est vrai que le Khayyam des Rubayiats n'avait été "révélé" qu'ne 1823! Ce premier traducteur, Woepke, nous révèle les six siècles d'oubli total de ce travail... et le siècle supplémentaire passé sans qu'il suscite un véritable intérêt:.
Prélude en Forme de Brève Histoire
En ouverture, Khayyam délivre une brève histoire du sujet, qui motive son travail et en justifie par avance la nouveauté: oui, on a déjà rencontré quelques problèmes du troisième degré , mais de façon disparate; non, personne n'a jamais tenté une étude générale et systématique. Voici ses premières phrases:
Petite incise pour comprendre la délicieuse image potagère qui l'accompagne: le traité d'Archimède
est si fameux (il contient une démonstration des volumes de ces deux
solides par comparaison et un problème de découpage par un plan
de la sphère en deux parties, qui mène à cette équation du troisième
degré) que son tombeau était, dit on, orné d'une sphère et d'un
cylindre. Disparu des mémoires, il fut effectivement retrouvé par
Cicéron, dont voici le témoignage:
Hélas, un nouvel effacement des mémoires advint, et ce que l'on présente aujourd'hui à Syracuse comme tombeau d'Archimède est bien douteux. Quant à Cicéron, son titre de gloire est ... celui de la honte de Rome, car il est considéré, à juste titre, comme la seule contribution aux mathématiques de la civilisation romaine. "Civilisation" à qui nous sommes donc redevables d'une triste quinzaine de siècles de retard et d'obscurantisme par la perte de l'héritage grec qu'auront su conserver et faire fructifier les mathématiciens du monde arabo-musulman, et tout particulièrement les Persans.
Reprenons, là où nous l'avons laissé, le texte de Khayyam, pour quelques propos qui seraient bien difficiles à dater si l'on gommait le nom de l'auteur (ainsi, Fourier n'aura-t-il pas à se plaindre, sept siècles plus tard, des vicissitudes du temps qui ont longtemps retardé la publication de sa Théorie Analytique de la Chaleur? ... pour ne rien dire des soucis des chercheurs contemporains...)
Avec ces mots, nous voilà dans notre objet.
Dit en langage moderne, Khayyam introduit, après l'inconnue x , toutes ses puissances, sans limite a priori:
Enfin, il précise avec soin les prérequis:
Un peu d'Ordre, pour commencer...
Khayyam dresse d'emblée une liste exhaustive des équations qu'il va étudier, qui ne contient pas moins de 25 cas différents! Rien d'étonnant en fait -même si cela peut surpendre le lecteur d'aujourd'hui- car deux raisons l'expliquent:
Nous vous proposons donc, à titre de comparaison, le texte très littéraire d'Omar Khayyam, et le tableau synoptique que nous pouvons en dresser avec les notations qui nous sont familères:
Les Cas connus et ceux qui s'y ramènent immédiatement
L'auteur reprend dans sa liste les six cas (du scond degré) envisagés par Al-Khowarizmi : [1], [2], [4], [7], [8], [9],
Le Cas du Problème d'Archimède
Notre dernière sélection, parmi les équations trinômes, est incontournable, puisqu'il
s'agit de celle issue du problème d'Archimède. Petit rappel du
propos cité dans l'introduction:
et commençons par le commencement, un coup d'œil à ce qu'a vraiment écrit Archimède, pour constater qu'il est encore très loin d'une formulation algébrique. Soyez attentif, car, d'une certaine manière... il va nous rouler!
La Solution à la Manière d'Omar Khayyam
Voici, d'une façon plus proche du texte source, la partie synthèse du raisonnement
| " Lorsque j'étais questeur à Syracuse, alors que tous autour de moi disaient ignorer où gisaient les restes d'Archimede, je résolus néanmoins de retrouver sa sépulture. Je savais en effet, par mes lectures, que le tombeau du grand géomètre était décoré d'une sphère et d'un cylindre. Je me mis à le chercher. Moi-même remarquai, au milieu d'un terrain vague qui tournait au sous-bois, après des jours de vaine quête, ce qui ressemblait, d'entre les buissons, à un tombeau couronné d'une boule de lierre. J'envoyai mes compagnons couper à la serpe le maquis et dégager l'ouvrage. Ensuite, avec l'émotion qu'on imagine, n'osant croire à mon bonheur, je m'approchai à petits pas. La base était nette de ronces, déjà, grâce à un zèle dont je félicitai chacun ; j'y lus une épitaphe, évanide, mais que je sus déchiffrer. C'était bien le monument du grand homme. Et c'est moi, ton frère, Marcus Tullius, qui suis né dans le modeste bourg d'Arpium, qui ai mis au jour et rendu à la lumière et à l'admiration des hommes un des plus poignants témoignages du génie humain." Cicéron, Lettre à son frère Quintus in Les Tusculanes
|
Hélas, un nouvel effacement des mémoires advint, et ce que l'on présente aujourd'hui à Syracuse comme tombeau d'Archimède est bien douteux. Quant à Cicéron, son titre de gloire est ... celui de la honte de Rome, car il est considéré, à juste titre, comme la seule contribution aux mathématiques de la civilisation romaine. "Civilisation" à qui nous sommes donc redevables d'une triste quinzaine de siècles de retard et d'obscurantisme par la perte de l'héritage grec qu'auront su conserver et faire fructifier les mathématiciens du monde arabo-musulman, et tout particulièrement les Persans.
Reprenons, là où nous l'avons laissé, le texte de Khayyam, pour quelques propos qui seraient bien difficiles à dater si l'on gommait le nom de l'auteur (ainsi, Fourier n'aura-t-il pas à se plaindre, sept siècles plus tard, des vicissitudes du temps qui ont longtemps retardé la publication de sa Théorie Analytique de la Chaleur? ... pour ne rien dire des soucis des chercheurs contemporains...)
"Quant
à moi, j'ai désiré et désire encore ardemment connaître avec certitude
toutes leurs espèces, et distinguer, par des démonstrations, parmi les
formes de chacune d'elles, les cas possibles des cas impossibles: je
sais en effet qu'on en a un besoin très urgent lorsqu'on est aux prises
avec les difficultés d'un problème. Je
n'ai pu cependant me consacrer exclusivement à la quête de ce bien, ni
y penser avec persévérance, détourné que j'en étais par les
vicissitudes du temps. Car nous avons été éprouvés par le
dépérissement des hommes de science, à l'exception d'un groupe aussi
petit en nombre que ses afflictions sont grandes, et dont le souci est
de saisir le temps au vol pour se consacrer pendant ce temps à
l'achèvement et à la connaissance certaine de la science. Or, la
plupart de ceux de notre temps qui font les savants, déguisent le vrai
en faux, ne dépassent jamais les limites de l'imposture et de
l'ostentation savante, et n'emploient la quantité de science qu'ils possèdent qu'à des fins corporelles et viles." [...]
Avec le concours de Dieu et Sa précieuse assistance, je dis: l'art de l'algèbre et d'al-muqabala est un art scientifique dont l'objet est le nombre absolu et les grandeurs mesurables, en tant qu'inconnus mais rapportés à une chose connue par laquelle on peut les déterminer [...]; l'accomplir consiste à connaître les méthodes mathématiques par lesquelles on peut saisir cette espèce évoquée de déterminations des inconnues, numériques ou géométriques." O. K. , Traité d'Algèbre
|
Avec ces mots, nous voilà dans notre objet.
"
Les grandeurs sont les quantités continues, qui sont quatre: la ligne,
la surface, le corps et le temps, comme on le trouve exposé d'une
manière globale dans les Catégories [d'Aristote]. [...]
Il n'est pas d'usage de de mentionner le temps au nombre des sujets des
problèmes de l'algèbre; mais si on l'avait fait, ç'eût été légitime. Il
est de coutume, chez les algébristes, de nommer dans leur art
l'inconnue qu'on veut déterminer «chose», son produit par elle-même «carré», son produit par son carré, «cube», le produit de son carré par son semblable «carré-carré», le produit de son cube par son carré «carré-cube», le produit de son cube par son semblable «cubo-cube», et ainsi de suite aussi loin qu'on veut."
O. K. , Traité d'Algèbre
|
| " Pour représenter l'inconnue
dans ce traité d'algèbre, Khayyam utilise le terme arabe chai, qui
siginfie «chose»; ce mot,
orthographié Xai dans les ouvrages scientifiques espagnols, a été
progressivement remplacé par sa première lettre, x, devenue symbole
universel de l'inconnue. " Amin
Maalouf,
Samarcande.
|
Dit en langage moderne, Khayyam introduit, après l'inconnue x , toutes ses puissances, sans limite a priori:
x , x2 = x × x , x3 = x2 × x , x4 = x2 × x2 , x5 = x3× x2 , x6 = x3 × x3 , .....
mais il ne va pas tarder à se restreindre, par pragmatisme, aux trois premières "Et si l'algèbriste emploie le carré-carré,
dans des problèmes de géométrie, c'est métaphoriquement, , et non pas
proprement, étant donné qu'il est impossible que le carré-carré fasse partie des grandeurs. Ce qui se trouve dans les grandeurs, c'est d'abord une seule dimension, c'est à dire la racine, ou, rapporté à son carré, le côté. Puis les deux dimensions, c'est à dire la surface -le carré dans les grandeurs est donc la surface carrée. Enfin, les trois dimensions, c'est à dire le corps -le cube dans les grandeurs est le solide limité par six carrés.. Or, comme il n'existe aucune autre dimension, ne font partie des grandeurs ni le carré-carré, ni, à plus forte raison, ce qui lui est supérieur." O. K. , Traité d'Algèbre
|
Enfin, il précise avec soin les prérequis:
" Il faut bien savoir que ce traité ne sera compris que de ceux qui maîtrisent le livre d'Euclide sur les Éléments et son livre sur les Données, ainsi que les deux premiers livres de l'ouvrage d'Apollonius sur les Coniques . Celui à qui la connaissance d'un de ces trois livres fait défaut ne peut avoir accès à la compréhension de ce traité. Je me suis du reste appliqué, avec peine, à ne renvoyer qu'à ces trois ouvrages." O. K. , Traité d'Algèbre
|
|
| exemplaire des Coniques d'Apollonius en langue arabe |
Un peu d'Ordre, pour commencer...
"Les solutions en algèbre ne s'effectuent que par l'équation, je veux dire en égalant ces degré les uns aux autres, comme on le sait bien." O. K. , Traité d'Algèbre
|
Khayyam dresse d'emblée une liste exhaustive des équations qu'il va étudier, qui ne contient pas moins de 25 cas différents! Rien d'étonnant en fait -même si cela peut surpendre le lecteur d'aujourd'hui- car deux raisons l'expliquent:
- il sépare d'abord en trois familles, selon le nombre de termes présents dans l'équation;
- il suit le principe posé par Al-Khowarizmi pour le second degré dans son Traité d'Algèbre, en discutant selon le nombre de termes présents de part et d'autre de la "balance" qu'est le signe =.
- x2 + x - 2 = 0 mais x2 + x = 2 ;
- x2 - x + 2 = 0 mais x2 + 2 = x ;
Nous vous proposons donc, à titre de comparaison, le texte très littéraire d'Omar Khayyam, et le tableau synoptique que nous pouvons en dresser avec les notations qui nous sont familères:
| Traité d'Algèbre, dans la traduction de Woepke |
||
| binômes |
trinômes | quadrinômes | groupe |
[1] bx = c [2] ax2 = c [3] x3 = c [4] ax2 = bx [5] x3 = bx [6] x3 = ax2 | [7] x2 + bx = c [8] x2 + c = bx [9] x2 = bx + c [10] x3 + ax2 = bx [11] x3 + bx = ax2 [12] x3 = ax2 + bx |
[19] x3 + ax2 + bx = c [20] x3 + ax2 + c = bx [21] x3 + bx + c = ax2 [22] x3 = ax2 + bx + c |
I |
" Nous ignorons tous deux les secrets absolus. Ces problèmes jamais ne seront résolus. Il est bien question de nous derrière un voile; Mais quand il tombera, nous n'existerons plus. " |
[13] x3 + bx = c [14] x3 + c = bx [15] x3 = bx + c [16] x3 + ax2 = c [17] x3 + c = ax2 [18] x3 = ax2 + c |
[23] x3 + ax2 = bx + c [24] x3 + bx = ax2 + c [25] x3 + c = ax2 + bx |
II |
N.B.: nous avons respecté, à l'intérieur de chaque espèce, les groupes faits par l'auteur.
en gras, les équations dont la résolution est nouvelle; en couleur, celles auxquelles nous limiterons cette présentation.
en gras, les équations dont la résolution est nouvelle; en couleur, celles auxquelles nous limiterons cette présentation.
Les Cas connus et ceux qui s'y ramènent immédiatement
L'auteur reprend dans sa liste les six cas (du scond degré) envisagés par Al-Khowarizmi : [1], [2], [4], [7], [8], [9], Un Binôme
 |
[3] x3 = c | ||
|
|||
|
Ainsi, Khayyam sépare très clairement la preuve (en l'occurence géométrique) d'existence de racines d'une équation (de façon générale) de leur calcul numérique:
loin de nier l'importance de celui-ci (en qualité d'astronome, il sait
mieux que quiconque que ce métier requiert des tables trigonométriquesprécises, et que sin 1° s'obtient à partir de sin
3° en résolvant une équation du troisième degré). La meilleure preuve
en est son affirmation : il a sur ce sujet écrit un traité... qui,
hélas, est demeuré introuvable, certainement perdu! Après cette
fugitive indication, il ne parlera plus ici que de la théorie des
équations.
x3 = c, la plus simple -mais la mère de toutes les équations du troisième degré- est ramenée par lui à l'intersection de deux paraboles,
de même sommet et d'axes perpendiculaires. Pour le dire rapidement, il
regarde l'unique racine positive comme l'intersection, hors le sommet,
des deux paraboles:y= x2 ; y2 = cx
Mais littéralement, les choses sont
dites de façon un peu plus compliquée... au moins pour nous, lecteurs
d'aujourd'hui. Cette intersection de courbes est donnée comme solution
du puisque le report de la première dans la seconde fournit x4 = cx.
Diable! Qu'est-ce que cela signifie-t-il? Qu'étant donnés AB (ici, de longueur c) et BC (ici, de longueur 1) , on cherche x = BI et y = BH tels que 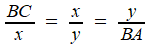 (*) (*)Un point D est sur la parabole " de sommet B, d'axe AB, et de côté droit AB" dans la terminologie d'Apollonius, reprise par Khayyam, signifie que ses projections I sur AB, H sur BC sont telles que AB.DH = DI2 (nous écririons c.x = y2 -en rouge, ce qui est connu, c= 2p dans la représentation "usuelle" y2=2px... mais défense, avant Descartes, de recourir aux coordonnées du point! )
S'il est aussi sur la parabole " de sommet B, d'axe BC, et de côté droit BC", BC.DI = DH2, et, avec DI = BH,, BI = DH il vérifie: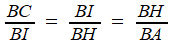 |
|||
Cette écriture en proportion continue (*) rappelle, et pour cause, l'approche d'Hippocrate de Chios pour le problème de Délos, alias la Duplication du Cube!
Lequel revient à la résolution de
x3 = 2
Apollonius crédite Ménechme de la
première utilisation, à cette fin, de l'intersection de 2
paraboles; son contemporain Ératosthène juge plutôt sévèrement: "Ménechme y réussit un peu, d'une manière laborieuse." Mais sans doute avec partialité, puisqu'il a sa propre machine à proposer, solution "mécanique" plutôt que géométrique. Notons que Khayyam ne dit rien de ces glorieux prédécesseurs dans son résumé historique.
|
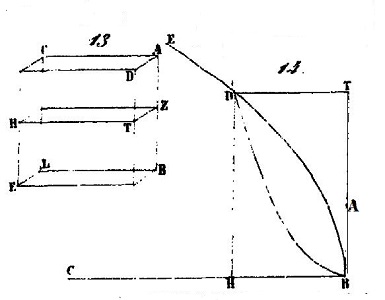 |
||
Quelques Trinômes
 |
[13] x3 + bx = c
|
|||
| On s'en doute, D est le point solution (plus précisément, son abcisse), et Khayyam va le démontrer. Mais peut-être est il utile de décrypter préalablement ce qu'il vient de dire, tout en traçant la figure correspondante. | ||||
Le nombre des racines désigne le coefficient de x (la racine, ou la chose), c'est à dire b. On l'assimile à l'aire d'un carré, pour que bx soit homogène à un volume; ainsi l'addition au cube de l'inconnue sera cohérente, et comparée au volume c, celui d'un paraléllépipède de base le carré d'aire b, ce qui en fixe la hauteur BC=c/b.
Khayyam fait sa synthèse de façon moins rapide, puisqu'il n'emploie pas les coordonnées; comme précédemment il use de proportions continues. AB est donc la racine carrée de b. Avec le même vocabulaire que dans le cas [3]. Khayyam affirme que la solution sera donnée par l'intersection:
| 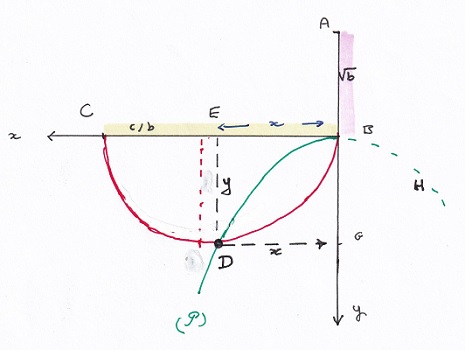 |
| Une autre manière de le dire rapidement, à
notre façon moderne, serait d'augmenter d'une unité le degré de
l'équation, en lui ajoutant la racine "factice" 0, dont on ne tiendra
pas compte. [13 bis] x4 + b x2 = c x
qui invite à poser y.√b= x2 pour retrouver une équation de cercle ( y = x2 serait
sans doute la première idée qui vienne, mais on déboucherait sur une
équation d'ellipse, courbe "plus compliquée" à tracer qu'un
cercle!) .
|
|
 |
[14] x3 + c = bx | |
|
||
|
... et ce point E fera
notre affaire. On remarque que tout le début de son discours (la mise
en place de la parabole) est similaire au cas [13]; le changement (en rouge) consiste à remplacer le cercle par une hyperbole. Cela apparaît clairement lorsque, par la voie la plus directe, on forme
[14 bis] x4 + c x = b x2
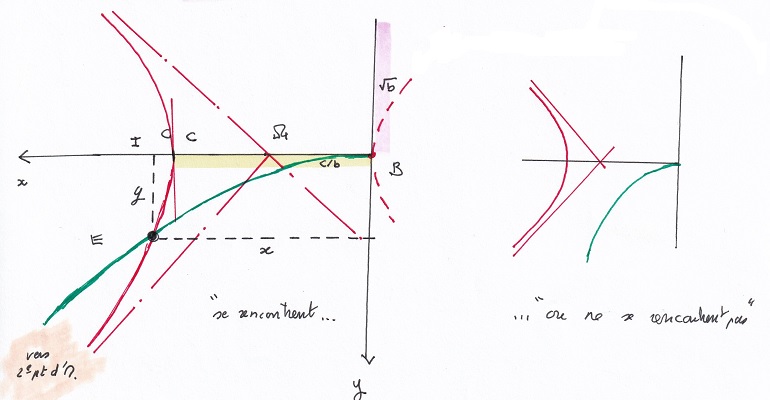 N.B. : lorsque Khayyam dit qu'une courbe est de position connue, cela signifie qu'elle est entièrement déterminée par les éléments donnés. La présence d'un deuxième point d'intersection 'une deuxième racine positive) est clairement mentionnée. L'adaptation, on le voit, a été réalisée de la manière la plus économique possible. |
||
Le Cas du Problème d'Archimède
Notre dernière sélection, parmi les équations trinômes, est incontournable, puisqu'il
s'agit de celle issue du problème d'Archimède. Petit rappel du
propos cité dans l'introduction:  |
[17] x3 + c = ax2 |
|
|
||
et commençons par le commencement, un coup d'œil à ce qu'a vraiment écrit Archimède, pour constater qu'il est encore très loin d'une formulation algébrique. Soyez attentif, car, d'une certaine manière... il va nous rouler!
 |
 |
| page-titre |
début du livre II, lettre introductrice. Il y signale notamment le fameux résultat sur le volume de la sphère! |
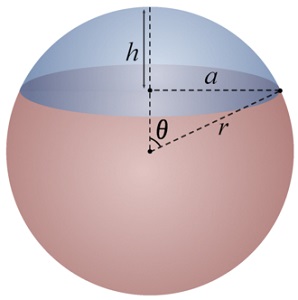 paramètres d'une calotte sphérique (image source: Wikimedia Commons) |
Sans
lire plus avant Archimède (cela peut être intéressant, mais la
digression serait trop longue!),voyons directement la mise en équation
du problème. Avec les notations ci-contre, le volume de la calotte
sphérique est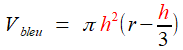 [voir cette page Wikipedia] [voir cette page Wikipedia]et par différence avec le volume de la sphère complète 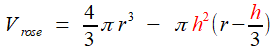 Demandons que le rapport du premier au second soit λ , nous aurons l'équation 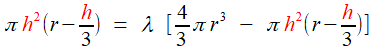 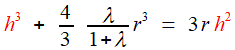 | |
|
[17] x3 + c = ax2
|
||
| Khayyam commence par poser c = H3,
par souci d'homogénéité: on additionne ainsi deux volumes, que l'on
compare avec un volume. Ce souci d'homogénéité "géométrique", que l'on
a remarqué plus haut dans le traitement de [13], est constant dans
l'ensemble du traité; on ne peut comparer que ce qui est comparable! Et s'il peut introduire ce nombre H, c'est par application de la résolution de [3], qui lui sert ici de lemme préparatoire. Il remarque ensuite (toujours dans l'optique: les coefficients et les racines ne peuvent être que des nombres positifs) que H < a. Le plus simple pour cela est d'écrire [17] sous la forme
[17 bis] H3 = x2 (a - x)
La racine cherchée sera nécessairement telle que 0 < x < a, d'où H < a par report. Puis, comme cette équation peut encore s'écrire H.H2/ x2 = (a - x) , il est naturel de faire intervenir * l'hyperbole 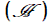 y = H2/ x , ou encore x y = H2 ( le carré est là pour l'homogénéité) ; y = H2/ x , ou encore x y = H2 ( le carré est là pour l'homogénéité) ;* la parabole 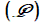 y2 = H (a - x) y2 = H (a - x)
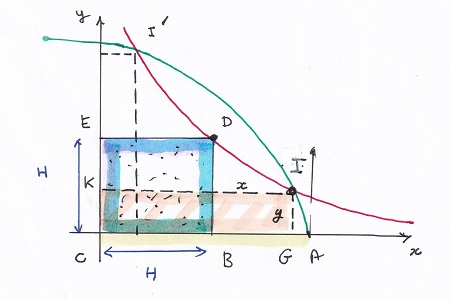
[ 17 bis] donnant, de manière évidente, les abcisses d'intersection des deux courbes. Khayyam construit 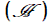 à l'aide d'un carré de côté BC = H : le point D (H , H) définit naturellement l'hyperbole avec les deux asymptotes. La parabole à l'aide d'un carré de côté BC = H : le point D (H , H) définit naturellement l'hyperbole avec les deux asymptotes. La parabole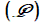 est, quant à elle, définie par AC = a. est, quant à elle, définie par AC = a. |
||
La Solution à la Manière d'Omar Khayyam
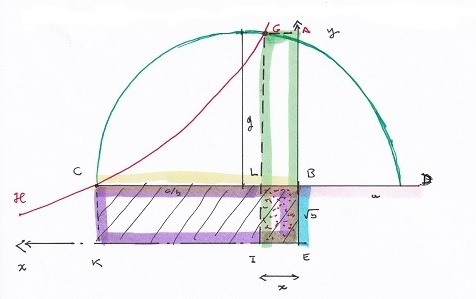
Voici, d'une façon plus proche du texte source, la partie synthèse du raisonnement Khayyam décrit les coniques à la manière d'Apollonius, c'est à dire, M étant le point courant dont les coordonnées seraient (x , y) , G et K leurs projections sur les axes.
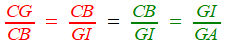 sur l'hyperbole sur la parabole Effectuons le produit des deux derniers, on aura grâce à la simplification des GI 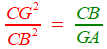 |
 |
|||||||||
| ça y est! Il tient par l'intersection des deux coniques la solution du lemme dont Archimède admettait implicitement le résultat! Il n'y a plus qu'à réécrire ceci CB3 = CG2. GA, soit c = H3 = x2 (a - x) |
||||||||||
Mais qu'en est-il de l'existence d'une solution? Est-elle vraiment prouvée, autrement dit: peut-on justifier que les deux courbes se coupent? Khayyam
est suffisamment convaincu de la nécessité d'argumenter sur ce point
pour l'articuler en trois cas. La discussion, basée sur la comparaison
des longueurs BC et CA, est quelque peu artificielle, mais elle a l'avantage de démarrer sur un cas particulièrement évident. Suivons le!
|
||
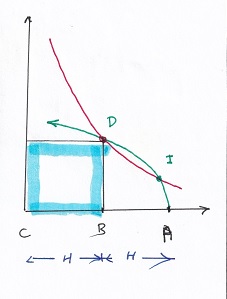 |
C'est l'avantage annoncé: le point D (introduit, rappellons le, pour définir complètement l'hyperbole) est solution évidente de l'intersection. Le "moindre examen" esprime
l'idée intuitive que l'hyperbole, passée sous la parabole, devra la
recouper pour se diriger vers son asymptote avant que le sommet de la
parabole ne soit rencontré. C'est plus ou moins un argument de valeur
intermédiaire, perçu comme évident (n'oublions pas qu'il le sera
jusqu'à la fin du XIXème siècle...)
|
|
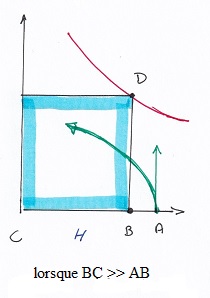 |
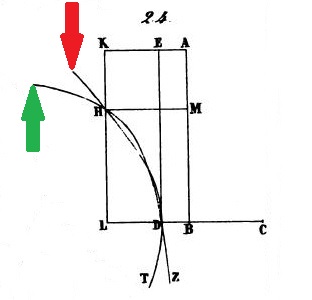
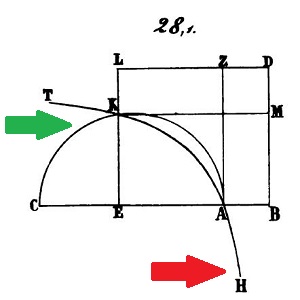
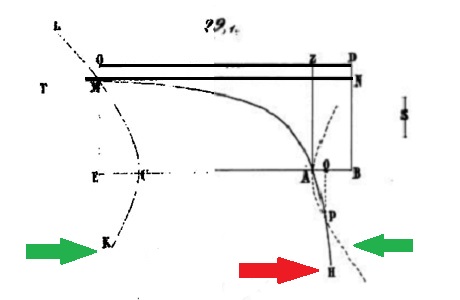
Celui que cite Khayyam n'a vu que le cas manifeste illustré ci-contre... Mais si l'on réfléchit bien en regardant "la première figure", une légère augmentation du côté du carré H déplace le point D vers le haut et la droite tout en maintenant deux points d'intersection (sauf dans le cas limite du contact tangentiel, fugacement évoqué par notre auteur). C'est le cas du contact tangentiel qui sépare les cas possibles des cas impossibles; mais ce n'est jamais dit explicitement. On pourra s'exercer à déterminer la condition sur a et c pour qu'il se produise... |
|
C'est la figure que nous avons choisie pour illustrer la résolution de Khayyam. |
||

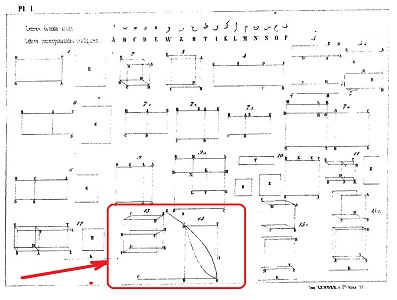





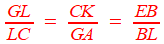
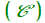
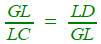
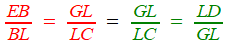
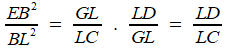



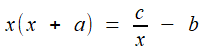
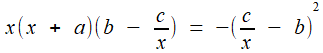
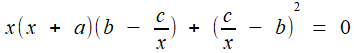
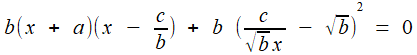
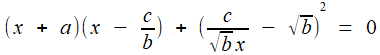
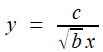 ;
; 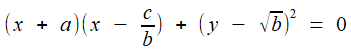
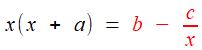
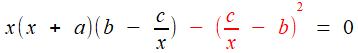

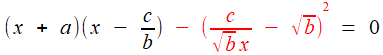
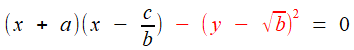

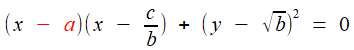


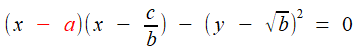


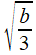 , et
, et 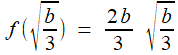 , que l'on compare à
, que l'on compare à 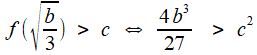
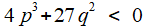
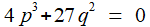 signe la présence d'une racine double.
signe la présence d'une racine double. 

