Fin (s?) de l'histoire...
Le Mémoire de Wantzel
Reçu à l'École Polytechnique en 1832, Laurent
Wantzel (1814-1848) poursuit ses études à
l'École des Ponts &
Chaussées (1834-1837). C'est alors qu' il résoud enfin la
question
initiale, jusque là sans réponse, constituant avec les
deux suivantes le legs de la Grèce Antique:- (Q1) La Duplication du Cube est elle résoluble à la Règle et au Compas?
- (Q2) La Trisection de l'Angle est elle résoluble à la Règle et au Compas?
- (Q3) La Quadrature du Cercle est elle résoluble à la Règle et au Compas?
- (Q4) Quels sont exactement les problèmes dont les solutions sont constructibles à la Règle et au Compas?
Le début de l'article de Wantzel dans le Journal de Mathématiques Pures et Appliquées,
dit Journal de Liouville
Il
apporte ainsi la preuve d'un résultat que l'on conjecture depuis
Descartes,
mais à qui il manquait essentiellement une formulation
précise:
"...ainsi l'inconnue principale du problème s'obtiendra par la résolution d'une série d'équations du second degré dont les coefficicients seront fonctions rationnelles des données de la question et des racines des équations précédentes. D'après cela, pour reconnaître si la construction d'un problème de Géométrie peut s'effectuer avec la règle et le compas, il faut chercher s'il est possible de faire dépendre les racines de l'équation à laquelle il conduit de celles d'un système d'équations du second degré composées comme on vient de l'indiquer."
"En somme, à l'époque de Descartes, on savait que toute expression algébrique, ne contenant que des radicaux carrés, est constructible à l'aide de la règle et du compas et inversement.
Nous allons maintenant préciser cet énoncé encore très vague: il faut indiquer par rapport à quoi l'expression est algébrique et quelles sont les données. Cela ne fut exprimé clairement qu'au xtx" siècle par l'introduction de la notion de domaine de rationalité "
Ce résultat est aujourd'hui un classique de la Théorie des Corps, mais on pourra constater à la lecture des textes que non seulement il n'est formulé qu'en termes d'équations par Wantzel, mais que la rédaction de Lebesgue, pour impeccable qu'elle soit, est encore très éloignée de celle qu'on peut proposer de nos jours en Licence de Mathématiques!
Lire l'article original de Wantzel (grâce à Wikisource)
N.B.:Avant lui, seul Gauss avait apporté une contribution nouvelle aux problèmes de constructibilité, en déterminant exactement quels sont les polygones réguliers constructibles. On trouvera dans cette page des corrélations Mathouristiques assez inattendues!
"...ainsi l'inconnue principale du problème s'obtiendra par la résolution d'une série d'équations du second degré dont les coefficicients seront fonctions rationnelles des données de la question et des racines des équations précédentes. D'après cela, pour reconnaître si la construction d'un problème de Géométrie peut s'effectuer avec la règle et le compas, il faut chercher s'il est possible de faire dépendre les racines de l'équation à laquelle il conduit de celles d'un système d'équations du second degré composées comme on vient de l'indiquer."
Wantzel, Recherche sur les Moyens [...]
"En somme, à l'époque de Descartes, on savait que toute expression algébrique, ne contenant que des radicaux carrés, est constructible à l'aide de la règle et du compas et inversement.
Nous allons maintenant préciser cet énoncé encore très vague: il faut indiquer par rapport à quoi l'expression est algébrique et quelles sont les données. Cela ne fut exprimé clairement qu'au xtx" siècle par l'introduction de la notion de domaine de rationalité "
Ce résultat est aujourd'hui un classique de la Théorie des Corps, mais on pourra constater à la lecture des textes que non seulement il n'est formulé qu'en termes d'équations par Wantzel, mais que la rédaction de Lebesgue, pour impeccable qu'elle soit, est encore très éloignée de celle qu'on peut proposer de nos jours en Licence de Mathématiques!
Lire l'article original de Wantzel (grâce à Wikisource)
N.B.:Avant lui, seul Gauss avait apporté une contribution nouvelle aux problèmes de constructibilité, en déterminant exactement quels sont les polygones réguliers constructibles. On trouvera dans cette page des corrélations Mathouristiques assez inattendues!
De l'autel de Délos... au
tapis de Sierpinski!
Il est intéressant, pour
finir, de constater combien l'analyse des erreurs peut être
fructueuse. De ce que nous disent Socrate et Eratosthène à la notion moderne de dimension fractale, si chère
à Benoît Mandelbrot (voir aussi sa HomePage),
il n'y a en
fait qu'un pas!
Considérons pour cela cet objet fractal qu'est le tapis de
Waclaw Sierpinski (1882-1969): il est construit en
retirant à la surface "pleine" d'un triangle
équilatéral le triangle construit sur les mileux des
côtés, et en réitérant à l'infini le
procédé sur les nouvaux triangles ainsi
définis.
Nous ne disons ni courbe (i.e.
de dimension 1), ni surface (i.e. de dimension 2), car nous ignorons
de quelle nature est cet objet, et notre but est
précisément de découvrir sa dimension, si tant est qu'il soit
raisonnable de lui en attribuer une! Nous parlerons donc de sa mesure. Comment la mesure m varie-t-elle dans une homothétie de rapport 2? Nommons M la nouvelle mesure:
- Courbe (dim =1)
:
M = 2.m
- Surface (dim =2)
:
M = 22.m = 4.m (voir Socrate!)
- Volume (dim =3) : M = 23.m = 8.m (voir Ératosthène!)
Comme le carré de
Socrate, le cube d'Ératosthène, le tapis de Sierpinki S est déduit du "petit" S1 par une homothétie de rapport 2.
On attend donc
M = 2d.m
Mais puisque le tapis S est réunion de 3 petits tapis
disjoints identiques à S1, on doit aussi avoir:
M = Mes (S) = Mes
(S1) + Mes
(S2) + Mes
(S3)= 3.Mes
(S1)
= 3.m
et par suite2d= 3
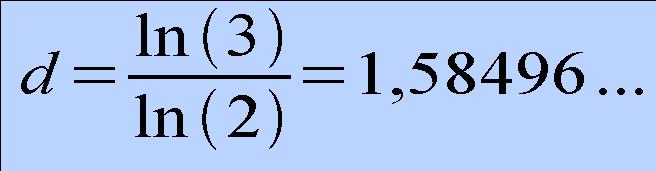
soit
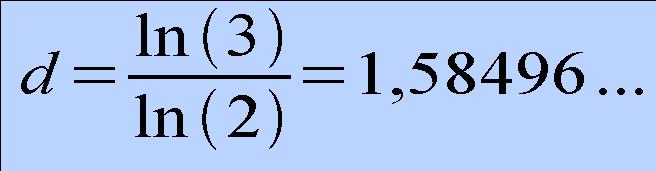
Le tapis de Sierpinski n'est donc ni
une courbe, ni une surface: la dimension qu'il est "raisonnable
de lui
attribuer" est clairement intermédiaire entre 1 et 2!



Revenir
à la Home Page du
Mathouriste