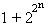Symétries
Polygonales d'Ordre Impair
On a déjà mentionné la
rareté de la
symétrie pentagonale; a fortiori s'étend-elle au
cas des
autres polygones d'ordre impair!
Symétrie
Triangulaire
Il est assez surprenant
tout de
même que cette rareté commence à
s'exercer... avec
un objet aussi commun que le triangle
équilatéral.
Certes, rien n'habite plus les objets de tous les jours que la
symétrie d'ordre 3: trépieds divers, du tabouret
de ferme
à la table de bistrot en passant par la suspension des
plateaux
de balance (telles qu'on en voyait encore beaucoup sur les
marchés de France dans les années 1960: il faut
aujourd'hui aller les chercher plus loin!)... et autres accessoires.
Bakhtapour
(Népal)
Mais existe-t-il des
bâtiments
ou corps de bâtiments en forme de prisme triangulaire? Sans
doute
l'angle aigu, et la perte d'espace à meubler qu'il implique,
ont-ils eu un rôle dissuasif...
Dans l'Antiquité
Voici néanmoins deux beaux monuments antiques de taille
respectable invariants par les groupes R
3 et
D
3, en
commençant par le plus célèbre,
édifié vers 330 av J.C.:
Musée
de
Delphes (Grèce): colonne des danseuses
Oui,
R3 et non D3, si l'on porte
bien attention à la position levée d'un des deux
bras!
En fait, on ne voit
là que la
partie supérieure d'une
colonne dont la hauteur est estimée à 13m : on
trouvera
plus de précisions
ici, et surtout
un intéressant
projet
de
reconstruction virtuelle qui ne manquera pas
d'intéresser
ceux qui, comme le Mathouriste, ont un petit penchant pour
l'Informatique Théorique: il exploite une structure de
données avancée, les
quadtrees!
(télécharger le document proposé:
dossier de
presse du 20/11/2003). Mais ce document permettra aussi de situer
l'emplacement de cette colonne géante dans le site, selon
une
perspective reconstruite.
Le second le bat en hauteur (23m), mais se signale avant tout par son
originalité: il s'agit d'un monument de style Carthagineois
(II-ème siècle avant J.C.), marquant
l'emplacement du
tombeau d'une riche famille. Or, la célèbre
imprécation
Delenda
est
Carthago ayant été prise au mot, peu
de
témoignages de cette brillante civilisation nous sont
parvenus!
Sabratha (Lybie):
Mausolée B,
Punique
À la Renaissance
C'est en 1642 que Francesco
Borromini
(1599-1667;
voir
aussi cette
biographie en Italien, c'est la version la plus
complète) signe, avec la
chapelle Sant'Ivo de l'Université La Sapienza à
Rome, un surprenant
(à plus d'un titre, on le verra dans ces pages!) chef
d'œuvre baroque: la symétrie triangulaire est le
principe
fondateur du monument.
Rome, Sant'Ivo de la
Sapienza (Italie) et son architecte Francesco Borromini
Rien ne le fait donc
soupçonner de l'extérieur. Mais entrez (ce qui
n'est pas
si facile: elle n'est ouverte que le Dimanche
matin, de 9h à 12h!); levez les yeux vers sa coupole. La
première perception
est hexagonale:
Regardez mieux, pour commencer, l'alternance des motifs
décoratifs: il y en a deux différents, chacun se
répétant trois fois: on est donc bien en
présence
d'une symétrie D
3! Laissez
descendre le regard vers les corniches, le meilleur est à
venir:
Les six "tranches" ont des bases alternativement convexes (en
demi-cercle) et concaves (un petit arc de cercle). Il y a donc 3
tranches du premier type, organisées en un triangle
équilatéral, et 3 du second, formant un
deuxième
triangle équilatéral, déduit du
premier par un
demi-tour.
Afin de vous aider à mieux saisir, nous avons
ajouté les
deux triangles servant de point de départ à cette
construction sur une photo prise avec un objectif "très
grand
angle" (cette coupole n'est pas très haute, contrairement
à la plupart de ses congénères
romaines, et rend impossible toute prise de vue d'ensemble à
l'aide des zooms équipant usuellement les appareils).
L'ensemble est donc bien invariant par le groupe D3,
puisqu'il est groupe de symétrie commun à ces
deux triangles.
L'image de fond de cette construction,
le
Mathouriste
l'a emprunté à ce
blog... que l'auteur soit ici
remercié de son invitation à aller admirer cette
église, qui prouve que l'on peut faire baroque et
léger,
alors que Rome a tôt fait de vous persuader de
l'incompatibilité des deux... Le propos de
Borromini
était bel et bien de
créer
une architecture refondée sur les principes de
l'antiquité, notamment la symétrie. [un autre
lien sur Sant'Ivo]
Motifs Décoratifs
Redonnons la parole à notre mentor, pour deux exemples
explicitement mentionnés dans son livre, le premier par le
texte seulement, le second acccompagné d'une photographie en
noir et blanc:
"L'exemple le plus
simple de symétrie de rotation [est] le trépied.
Si l'on veut éliminer la symétrie
réflexive qu'il possède, il suffit d'ajouter de
petits traits au bout des branches: on obtient alors le
triquètre, vieux symbole magique. Les Grecs l'ont
dessiné avec, au centre, la tête de la
méduse et en ont fait le symbole de la Sicile triangulaire."
(H.W.)
Les trois jambes symbolisent
ses trois
caps. Une aubaine pour trouver un exemple de groupe de
symétrie R
3
! En voici un exemple, qui décore
l'entrée d'une demeure du XIX-ème
siècle, devenue
un hôtel de luxe.
"Sur l'escalier au
dessin harmonieux de la chaire de la cathédrale
Saint-Étienne, la Stefankirche, à Vienne, un
cercle orné d'un triquètre alterne
avec un cercle
orné d'une croix gammée ." (H.W.)
Nous proposons deux autres exemples décoratifs; le premier
remonte à l'antiquité Romaine
Ostia Antica (Italie,
port de la Rome antique): plaque d'écoulement des eaux.
Le second, qui est aussi le plus récent (
XVIII-ème
siècle) , est l'originale girouette du château de
Peterhof,
résidence
estivale des tsars proche de Saint-Petersbourg. L'emblème de la Russie était alors un aigle
à deux
têtes, symétrique par rapport à son axe
médian (et il l'est redevenu). Pour qu'il soit vu ainsi de
n'importe quelle direction, et quelle que soit la direction du vent...
on a eu l'idée de construire un aigle à 3
têtes et
trois corps, chacun dans le plan vertical des hauteurs d'un triangle
équilatéral. L'illusion est saisissante!
Saint Petersbourg,
Peterhof (Russie)
Le Mathouriste reste en attente de
nouvelles découvertes...
Un Heptagone
Décoratif !
D7:
Gauss
a caractérisé dans ses
Disquisitiones
Arithmeticae (1801) les polygones réguliers
constructibles à l'aide de la règle et du compas:
pour n
< 25, voici le début de la liste:
3 , 4 , 5 , 6 , 8 , 10 ,
12 , 15 , 16
, 17 , 20 , 24 , ...
En fait, parce qu'on
sait construire
facilement la bissectrice d'un angle, et partant doubler le nombre de
côtés, on peut se restreindre aux nombres impairs,
et
même aux nombres premiers en employant un peu
d'arithmétique élémentaire. Ce qui
restreint la
liste ci-dessus à
3 , 5 ,17 , 257 , 65537 ,
...
et tous les
nombres
de Fermat
Fn =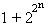 
à condition
qu'ils soient
premiers: ce brave
Fermat
croyait la chose automatique, mais il n'en était rien (pas
de
chance: après
n
= 0,1,2,3,4
qui fournissent les nombres ci-dessus,
n = 5, 6, 7
engendrent des F
n non
premiers; c'est
Euler
qui a découvert le premier, en 1732, que 641 divise F5)
Mais revenons à nos polygones: 7 est absent de la liste,
seule
une construction approchée peut être
effectuée.
D'autre part, pas plus que le pentagone, l'heptagone ne peut paver le
plan à lui tout seul. C'est donc un "plus mauvais candidat"
encore que le déjà rare pentagone.
Pourtant, regardez cet iwan... Le Mathouriste
a pris volontairement cette photo... mais
pour le
beau motif d'ordre 10 au fond et en face, sur le mur vertical. Quelle
n'a pas été sa surprise en
découvrant
sur l'image ce qu'il n'avait pas remarqué in
situ: la
partie qui se resserre en plafond, où plusieurs
étoiles régulières à 7
branches sont
présentes!
Mosquée
Jameh, Yazd (Iran)
Moralité:
méfiez vous
des belles chose, redoublez
d'attention: à observer le magnifique, vous risquez de
passer
à côté de l'exceptionnel!
Trouver la
symétrie
heptagonale sur une église est encore plus rare:
c'est
pourtant le cas sur une face de la cathédrale de Palerme.
Construite après la phase Arabe de l'histoire Sicilienne
(831-1071),
lors de la consolidation du régime des Rois Normands, de
1170
à 1190, elle conserve une part importante
-et surprenante- de décoration
géométrique. Il
faut dire que les souverains
Normands, s'ils étaient catholiques de religion, avainet
été fascinés par l'art de vivre
oriental, tant des
Byzantins que des Arabes: cette cathédrale, et celle de
Monreale, dont on reparlera un peu plus bas, en portent la marque par
un mélange de styles unique, mais sans faute de
goût.
Entouré d'une profusion de motifs à
symétries
d'ordre 4 et 8 (essentiellement), 6 parfois, apparait
une seule fois,
sur la façade arrière de l'église
(à droite
de l'abside, mais pas à gauche!) un motif à
symétrie D
7. Raté de
construction
ou...volonté
délibérée?
Abu
Al-Wafa (940-998) donnait dans son
Livre
des Constructions Géométriques
Nécessaires
à l'Artisan un procédé
approché de
construction de l'heptagone qui aurait pu suffire: affaire
à suivre...
Cathédrale de
Palerme (Sicile)
Et un dernier exemple artisanal, bien Français... mais dont
on
ne sous-estimera pas la valeur culturelle; d'ailleurs, n'a-t-il pas
été photographié dans un lieu
"à la
hauteur"?
Tastevin,
Musée des Hospices de Beaune (21)
R7:
Le groupe R
7 est encore plus discret, on s'en
doute... Le
Mathouriste
a fini par en dénicher deux exemples. Le premier dans le
portail
latéral de la cathédrale
précédente (qui
est un ajout postérieur du XV-ème
siècle):
Cathédrale de
Palerme (Sicile)
R
3
! Enfin le décor latéral présente une
invariance
par un R
n , où
n
est assez grand...
mais pas facile à évaluer de façon
certaine sans
ouvrir la vitrine, hélas...
Palerme (Sicile),
Musée
Archéologique
Et finalement... de
l'Architecture Heptagonale!
Le
Mathouriste
ne croyait plus en trouver un exemplaire quand il a eu la stupeur d'en
découvrir un. De surcroit, il n'est pas caché du
tout, et mieux: beaucoup de touristes passent juste à
côté de lui, sans porter attention à sa
particularité! Pourquoi? Parce qu'il se situe à
l'ombre du célèbre Platane
d'Hippocrate (voir aussi l'article
de
Wikipedia), dans l'île de Kos (Grèce).
Et la foule n'a d'yeux que pour l'arbre,
vénérable certes, mais tout de même pas
contemporain du Père de la Médecine...
C'est une petite
fontaine à ablutions: la photo en fait apparaître
tous
les piliers, vous pouvez donc vérifier! Le bassin
intérieur possède, lui, 14 panneaux de marbre, ce
qui constitue un doublement sans surprise. Un guide Turc nous a
assuré que des monuments similaires peuvent être
vus à Istanbul, mais
le
Mathouriste avoue son septicisme:
d'accord, on y trouve (presque) autant de fontaines polygonales que
de mosquées, mais la plupart sont octogonales, quelques
unes hexagonales... et s'il a eu le bonheur d'y voir un cas
décagonal,
aucune
réplique du modèle de Kos. La ville est grande, les
mosquées y sont nombreuses, il serait bien présomptueux
de prétendre avoir tout vu. Disons que l'heptagone ne se
présente pas au sein des monuments historiques les plus
marquants; si jamais il en est de plus secrètes... ce site
attend vos dons au cas où le hasard les
placerait sur vos promenades!
Mais en fait... n'y en aurait-il pas eu en France, tout simplement?
L'œuvre de Vauban semble plaider pour une réponse
positive, quoique nuancée: analyse en trois temps!
1) Oui catégorique si l'on se fie à cette gravure
de 1642.
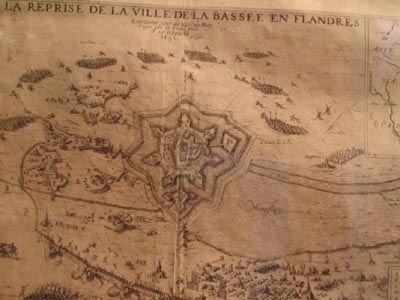Fortifications de La
Bassée (59) au XVIIème siécle
2) Mais
reflète-t-elle exactement la réalité?
Confrontée à un plan qui la montre sous forme
d'un octogone fort peu régulier, la
représentation
ci-dessus est suspecte quant à sa
fidélité.
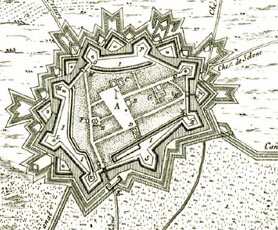Article
La
Bassée (59)
de Wikipedia
3) En revanche,
présent dans le "Jeu des Fortifications" (
voir la
page des
Symétries Pentagonales)
au même titre
que
le pentagone et l'hexagone, l'heptagone parait bel et bien
considéré
comme "citadelle théorique". Que l'on trouvera
réalisée avec une assez remarquable approximation
sur le
site de Maubeuge!
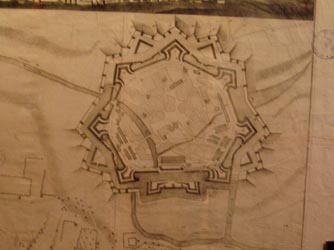Jeu des
Fortifications.... et réalisation concrète
à Maubeuge
Le lecteur peut
certes contester: un polygone "presque
régulier" n'est mathématiquement pas du tout
régulier! Mais avec six côtés
égaux
dès le premier coup d'œil, ce plan n'exprime-t'il
pas la volonté
de faire régulier,
quitte à ce qu'un ultime ajustement rendu
nécessaire par
l'adaptation au terrain en altère la lettre plus que
l'esprit?
Nous prendrons le rique de le penser.
L'Ennéagone,
lui aussi...
Encore
plus rare, pas davantage constructible: le polygone à 9
côtés.
Al-Biruni
(973-1048), notamment, s'était attaqué
en vain à sa détermination exacte, et
avait algébrisé le problème en le
ramenant
à une
équation du troisième degré
x³
+ 1
= 3
x
avant de parvenir
à une valeur
approchée.
L'ennéagone figure
en unique
exemplaire
sur l'abside de la cathédrale de Monreale, près
de
Palerme (à droite de l'abside, pas à gauche).
Cette
singularité n'a pas plus d'explication que celle de Palerme
ci-dessus: ces deux églises présentent des
similitudes...
jusque dans ces curieuses particularités.
Monreale (Sicile): motif
d'ordre 9 et
vue générale de l'abside
L'Heptadécagone
enfin
démasqué !
Revenons à Gauss et aux polygones
réguliers
constructibles. Il avait commencé
par découvrir la construction du polygone à 17
côtés dès 1796, à 19 ans. [
voir une méthode
possible ]
Il n'est cependant pas courant d'en observer un, ou, ce qui revient au
même, une division du cercle en 17 parties égales,
et le Mathouriste
n'aurait osé espérer seulement qu'on lui
indique où aller voir. Et puis, le jour où il s'y
attendait le moins...
Kremlin d'Aleksandroskaya Sloboda (Russie), Musée
Il s'agit du cadran
d'une horloge
conservée au musée du
Kremlin
d'Aleksandroskaya Sloboda, d'où Ivan IV le
Terrible dirigea
toute la Russie de1547 à1584. L'édification en
avait
été décidée par Basile III,
grand duc
Moscovite et oncle d'Ivan; elle était devenue
résidence
des tsars dès 1513, mais Ivan IV en avait fait son poste de
commandement principal.
Kremlin d'Aleksandroskaya Sloboda (Russie)
Pourquoi
la
division en 17? Parce qu'en ce lieu, la durée
maximale du
jour en été (ou de la nuit en hiver) est de... 17
heures.
Il n'a hélas pas été possible
d'obtenir sur place
plus de détails sur son fonctionnement, mais on
peut
supposer que l'horloge était
"réinitialisée" tous
les jours
(et toutes les nuits?..); sinon, comment faire?
Le cadran extérieur et/ou le cadran intérieur
était il-mobile, afin qu'ajustant les deux quadrants l'un
à l'autre
chaque jour, on puisse lire l'heure "classique" et savoir
où l'on en était de la durée du jour
(ou de la
nuit)? Pas évident, puisqu'ils sont tous deux
gradués en
17 parties.
Ce qui est sûr, c'est qu'en Russie les cadrans
d'église,
du
XVI-ème au XVIII-ème siècle, n'avaient
qu'une
seule aiguille, celle des heures, et que leur cadran était
marqué par des lettres, comme le cadran extérieur
de
celle-ci. (voir un
exemple
au Monastère Saint-Euthyme, à Suzdal, Russie).
Or, le A
correspond à 1 heure, le B à deux, etc... dans
l'ordre de
l'alphabet alors en usage. Que l'on voit bien face à face,
comme
s'il s'agissait seulement de donner le dictionnaire entre le code
alphabétique et le code numérique.
On peut tenir pour très probable que l'artisan a
utilisé
une division approchée plutôt que la fameuse
construction:
il n'y a pas de date apparente, mais l'objet semble
antérieur au
dix-neuvième siècle.
Une vue un peu plus large fait voir une partie du mécanisme,
...
dont on ne tire pas à première vue d'information
décisive.
Le
Mathouriste
remercie les guides du
musée, qui l'ont autorisé à prendre
ces
clichés.
Toute information
complémentaire sera évidemment
accueillie avec une grande reconnaissance!
N.B.: On peut voir au
Musée
des Arts et Métiers à Paris une
curieuse
horloge révolutionnaire, possédant une
double
graduation, l'une en 24h, l'autre en 10 parties: il s'agissait d'une
tentative -certains diraient: d'un excès de zèle-
pour
appliquer au temps la division décimale à
l'époque
de l'instauration du système métrique. C'est
complètement différent de notre cas,
où l'heure
demeure la 24-ème partie de la journée.
Mais il y a plus étonnant encore. Le bassin des Aghlabides
à Kairouan est formé par deux
réservoirs de forme
polygonale: le grand bassin est un polygone régulier
à 48
cotés, inscrit dans un cercle de diamètre 128m ,
et
le petit bassin,
de
décantation, inscrit dans un cercle de diamètre
37,4 m,
est un polygone
à 17 cotés:
or la construction date du
IX-ème siècle (achevé en 862)! Nous
empruntons les
deux
vignettes-plans ci-dessous à
ce
site.
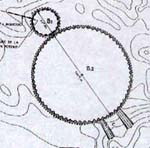
Kairouan (Tunisie)
Grâce
à la complicité de Roger Hanoune,
archéologue
(Université de Lille-III), le
Mathouriste
est désormais en mesure d'en apporter la
preuve par
l'image:
Vue
Générale
Plan de Kairouan: les
bassins sont en
haut!
Les 2 bassins
Kairouan (Tunisie): le
bassin
à 17 côtés
On
distingue mieux la forme à l'intérieur, car
à
l'extérieur, outre des contreforts aux angles, les murs en
possèdent un supplémentaire à chaque
milieu de
côté; en face, à
l'intérieur, se trouve une
petite niche.
Selon le géographe qui en a rapporté la
construction,
El-Bekri, sa construction est à porter au
crédit
d'Abu Ibrahim Ahmed, fils de Mohammed l'Aghlabide. Il était
alimenté par un aqueduc long de 36km.
N.B: Qui sont les Aghlabides? : notre lien vers la
réponse
de
Wikipédia.
