Si vous n'êtes
pas féru de trigonométrie,
vous pouvez bien sûr sauter le petit calcul qui suit; mais
retenez quand même ce
point-clé, tant de l'astronomie que de la
géodésie: il est (relativement) facile de
mesure des angles, et difficile (voire impossible) de mesurer des
distances.
D'où l'intérêt de mesurer les premiers,
et d'en
déduire par le calcul les secondes! La
trigonométrie
n'est pas un plaisir vicieux, (ah... ces méchantes formules
à apprendre! Et le prof' qui va vous coïncer...)
mais un
outil précieux.
| Déterminer le Rayon
de la Terre... |
... grâce à
la détermination préalable de la hauteur
d'une montagne |
|
|
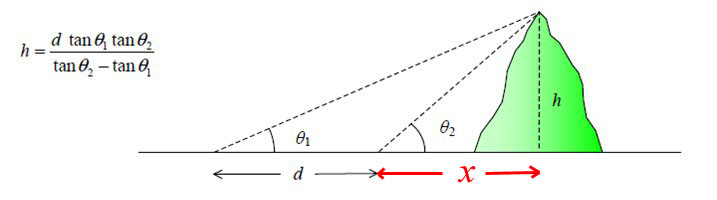
Dans un premier temps,
on détermine h
à l'aide de deux points au niveau de la mer, distants de d mesurée
précisément. On réalise pour cela deux
visées (à l'astrolabe) du sommet de la montagne
à
partir de ces deux points; toute la figure doit rester dans un
même plan vertical. Les angles θ1
et θ2
sont alors connus, ainsi que d; par contre la
distance x
ne l'est pas, et sa mesure est de surcroît impraticable. Mais
on a, en comparant les deux:
h = (d + x) tan
θ1
= x tan
θ2
Des
deux dernières, on tire x
en fonction de d, on
reporte... c'est fini!
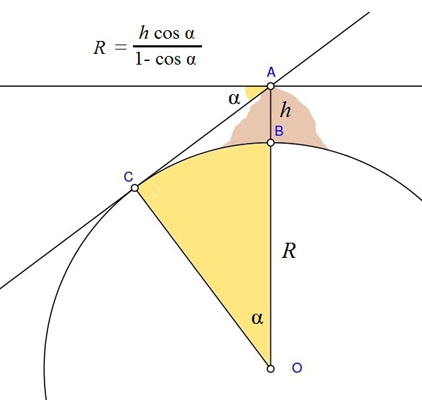
Dans
un deuxième temps,
on se place en haut de la montagne; avec un fil à plomb, on
a la
verticale, donc l'horizontale. On vise l'horizon selon AC,
définissant ainsi un angle α
mesuré avec l'astrolabe.
Grâce à l'égalité
des angles à côtés
perpendiculaires, on trouve
R = (R + h) cos α
dont
on tire la valeur de R.
|
Et
c'est ainsi qu'il trouva pour valeur R =
6339km (convertie au système
métrique); la valeur moyenne de
référence d'aujourd'hui est
R =
6371km !
|
Indépendamment,
il fit une mesure d'un degré de méridien
terrestre, entre Gorgan (aujourd'hui en Iran, à la
pointe Sud-Est de la Mer Caspienne)
et Ghuzz (Dihistan, Turquie); là encore, comme plus tard
avec
Delambre et Méchain pour la définition du
mètre,
point de salut hors de la trigonométrie. Cette mesure devait
être reprise et précisée, mais son
mécène d'alors, Qabus,se
désintéressa du projet. Ce prince Ziyaride avait
attaché Al-Biruni à sa cour, à Gorgan
; Al-Biruni lui avait dédié sa
Chronologie des Peuples Anciens,
ouvrage de référence pour la connaissance des
calendriers
anciens: grec, perse, arabe, qui y sont étudiés
et
comparés avec grande précision. Sans lui, le
calendrier
soghdien serait demeuré incompris, et l'histoire du Khorezm
avant la conquête arabe totalement méconnue.
Peu de témoignages nous restent de cette période,
sinon l'extraordinaire tour funéraire que le prince
se fit
construire de son vivant (1006-1007), et qui a la double
particularité d'être
la plus haute tour en briques au
monde, et un monument à
base décagonale,
ce qui est particulièrement rare (et lui vaudra
bientôt les honneurs de
notre page dédiée).
Le
Courrier de l'Unesco
n'ayant pas hésité
à vous
en proposer l'image dans son numéro spécial du
millénaire d'Al-Biruni, le
Mathouriste
ne résistera pas à l'envie de le concurrencer
quelques années plus tard... et en couleurs!
Le
Gonbad-e-Qabus, à
Gorgan (Iran); carte issue de Wikipedia.
 |
"L'Alborz
commençait maintenant à s'incurver devant nous,
déterminant une baie de verdure. Au centre de cet espace,
à trente kilomètres de distance, une fine
aiguille
crème se détachait sur le bleu des montagnes -la
tour de
Kabous. [...] La tour, au nord du bourg, prend son élan vers
le
ciel à partir d'un petit monticule vert de forme
irrégulière -mais artificiel, très
ancien.
[...]
Dedans, il n'y a
rien. La
dépouille de Kabous se trouvait ici, dans un cercueil de
verre
accroché sous le toit. Kabous mourut en 1007. Mille ans
durant,
ce phare a rappelé l'existence du souverain et le
génie
de la Perse aux peuples nomades de la mer d'Asie Centrale. [...]
Les termes hyperboliques utilisés par les voyageurs pour
décrire des objets qu'ils ont vu, mais que n'ont pas vu les
autres, ont bien souvent quelque chose de suspect. Je le sais, pour
m'être déjà rendu coupable de ce
péché. Mais relisant ce journal à deux
ans de
distance
[...], je persiste dans l'idée que j'avais conçue
avant de partir pour la Perse; [...] à savoir que le Gonbad-e-Kabous est
à mettre au rang des plus hautes réalisations
architecturales de l'humanité."
|