Al Tusi,
d'Alamut à Maragheh
Nasir al-Din al-Tusi (1201-
1274) a quitté les ruines fumantes d'Alamut; il a su se
montrer
convaincant auprès du prince seldjoukide Hulagu Khan: non
seulement il a été épargné,
mais il a
gagné sa confiance, au point d'obtenir qu'on lui construise
un
observatoire à Maragheh.Est-ce en promettant au souverain de
lui
faire des horoscopes fiables s'il peut observer les astres avec
précision? Il ne serait ni le premier, ni le
dernier...
Deux petites observations sur ce joli timbre, centré sur son activité d'astronome:

Deux petites observations sur ce joli timbre, centré sur son activité d'astronome:
- Notez le lutrin sur lequel repose un livre; l'objet est typique d'Asie Centrale (Iran, Ouzbékistan, Azerbaïdjan...)
- Ce timbre a été émis par la république d'Azerbaïdjan, qui le considère donc comme un de ses hommes illustres. Or, Tus, Alamut et Maragheh sont toutes situées dans l'Iran actuel... mais Maragheh est dans la région de l'Azerbaïdjan Iranien, ce qui légitime d'une certaine manière cette fierté nationale, au delà des frontières modelées par une histoire turbulente.
Épisode II : le Magicien de Maragheh
Les Bâtiments de l'Observatoire
L'arrivée au site... provoquera un choc au visiteur non préalablement averti! Mais qu'est-ce que cette espèce de dôme géodésique à la Buckminster Fuller (voir notre page sur les sphères en architecture) fait là?Il s'agit en fait d'une
construction
de l'époque du dernier shah, obsédé
par le
modèle américain dans son désir de
modernité... Elle remplit sa mission: protéger le
peu qui
reste du bâtiment principal, mais 'adaptation au site est
évidemment (plus que) discutable, même pour qui
apprécie les dômes
géodésiques ( et le Mathouriste
est plutôt de ce camp-là. De là
à en mettre
n'importe où...). Encore que ce soit, à tout
prendre,
moins laid que les toits en tôle ondulée qui
gênent
le regard sur beaucoup de sites archéologiques.
Les deux stèles au premier plan présentent le plan du site -fort utile- et un historique sommaire (en Persan seulement).
Un terrain de 280m sur 220m fut choisi et aplani au sommet d'une colline dominant la ville. La construction ommença en 1259 pour s'achever en 1263: Al-Tusi avait donc su convaincre rapidement son nouveau protecteur , non seulement du bien-fondé de sa requête, mais aussi de diligenter les travaux. L'activité en est enregistrée de 1265 à 1316, date de la mort de son dernier directeur connu, Asil-al-Din, qui avait pris ses fonctions en 1304. D'autres témoignages attestent un état de ruine en 1350, dont l'origine pourrait être des tremblements de terre successifs. Et, malheureusement, dès qu'un bâtiment se dégrade, voire simplement n'est plus utilisé, il est fréquent qu'il soit traité comme une simple carrière où l'on vient se fournir en pierres!
De ce qui fut le plus grand observatoire de son époque nous restent donc de nettes implantations au seul niveau du sol.
Les deux stèles au premier plan présentent le plan du site -fort utile- et un historique sommaire (en Persan seulement).
Un terrain de 280m sur 220m fut choisi et aplani au sommet d'une colline dominant la ville. La construction ommença en 1259 pour s'achever en 1263: Al-Tusi avait donc su convaincre rapidement son nouveau protecteur , non seulement du bien-fondé de sa requête, mais aussi de diligenter les travaux. L'activité en est enregistrée de 1265 à 1316, date de la mort de son dernier directeur connu, Asil-al-Din, qui avait pris ses fonctions en 1304. D'autres témoignages attestent un état de ruine en 1350, dont l'origine pourrait être des tremblements de terre successifs. Et, malheureusement, dès qu'un bâtiment se dégrade, voire simplement n'est plus utilisé, il est fréquent qu'il soit traité comme une simple carrière où l'on vient se fournir en pierres!
De ce qui fut le plus grand observatoire de son époque nous restent donc de nettes implantations au seul niveau du sol.
Fondations de
bâtiments 9 et 10 (voir plan)
Même en ruines, l'observatoire impressionnera et inspirera fondamentalement un visiteur et grand astronome : Ulugh-Beg lui-même, qui tracera les plans de l'observatoire de Samarcande à partir de ceux de Maragheh. Il inspirera aussi le rsouverain Moghol Jaï-Shing, qui fera construire, toujours sur ce modèle, l'observatoire de Jaïpur. Celui-ci, fort bien conservé (promis, le Mathouriste vous en reparlera plus longuement un jour prochain...), donne une idée de l'aspect imposant des instruments de Maragheh.et Samarcande.

Al-Tusi entouré de son équipe à l'observatoire de Maragheh
Source: blog de Parviz Tarikhi, physicien iranien.
Notre héros était loin d'être seul dans
son
laboratoire: contrairement à ce qui devait se passer par la
suite en Europe, où Copernic, Tycho-Brahé et
Képler
ne travaillaient guère qu'avec quelques aides non
qualifiés, et un ou deux disciples (ce fut le cas de
Képler auprès de Tycho) quand ils
n'étaient pas
seuls, il était entouré d'une équipe
scientifique
de très haut niveau, si bien qu'on a pu parler d'une
École de Maragheh. On relève les noms de
Muayyid a-Din-e Orouzi, Fakher
a-Din-e Maraghi, Fakher a-Din-e Ekhlati, Najm a-Din-e Dabiran et, tout
particulièrement, Muayyid
al-Din-al Urdi., principal responsable de la construction des
instruments. Al-Tusi souhaitait lancer un programme d'observation sur
30 ans (période de révolution de Saturne), comme
à
l'observatoire d'Isfahan dirigé par Omar Khayyam, d'autant
que
ce dernier ne les avait pas atteint en durée de
fonctionnement..
Mais il avait dû réduire ses ambitions
à une
durée de 12 ans, soit la période de Jupiter.
Car tout cela avait un coût important: bâtiments, instruments, entretiens, salaires du personnel... Hulagu Kahn innova économiquement, en finançant tout cela grâce aux biens de main morte (ou waqf: en droit islamique, donation à perpétuité d'un particulier pour financer une œuvre d'utilité publique).
Outre le grnad quadrant méridien évoqué, voici le type d'instrument qui devait équiper les petites tours adjacentes ( repères 9 du plan):
L'instrument 1 est classique, on le trouvait déjà à Ravy ou Isfahan; Avicenne le décrit également. Le bras A peut tourner de 360° autour de l'axe de la tour, tandis que le bras B se meut dans le plan vertical de A (grâce à la coulisse C); la combinaison des deux permet de viser n'importe quel astre. mesure l'azimut de l'étoile, On mesure alors l'azimut avec A (observer que le haut de la tour est gradué) et la hauteur sur l'horizon avec B. Ces deux angles sont un peu moins familiers que les coordonnées longitude et latitude ne le sont aujourd"hui; pourtant il s'agit du même principe de coordonnées orthogonales sur une sphère, comme le petit tableau qui suit vous le rappelle.
Tout le génie de l'astrolabe consiste d'ailleurs à automatiser le passage d'un système de coordonnées sphériques à l'autre, en ayant aplati le tout en deux dimensions grâce à une projection bien chosie.
L'instrument 2 a été conçu par Al-Urdi pour cet observatoire; il permet de mesurer simultanément, selon le principe de l'instrument1, deux positions d'astres différentes (l'une avec le quart de cercle A, l'autre avec B) -sans doute pour conduire plus rapidement les calculs de comparaison. Ces quarts de cercles remplacent la coulisse C de .l'instrument 1; ils décrivent entièrement une hémisphère lorsque lon fait varier l'azimut. C'est moins rustique, plus précis, mais sans doute bien plus cher à la fabrication!
Le résultat fut la constitution des tables Ilkhanides (Zīj-i Īlkhānī), ainsi nommées en l'honneur de la dynastie d'Hulagu; de fait, elles ne furent publiées que sous le règne de son fils, en 1272. Soit quasi immédiatement après la réalisation du programme de 12 ans lancé à la mise en fonction! Leur qualité leur valut d'être traduite du Persan vers l'Arabe et d'être utilisée jusqu'au XVème siècle. La précession des équinoxes (page anglosaxonne beaucoup plus riche) calculée était de 51" d'arc par an;, la valeur établie aujourd'hui est de 50",2 et la précision de l'évalutaion de Maragheh reste saluée comme remarquable par toutes les histoires de l'astronomie.
Le manuscrit donne, à la manière d'une chronophotographie, les passages aux 4 instants qui divisent le temps de parcours sur le cercle noir en 4 intervalles égaux; la valve se trouve alors aux extrémités du diamètre du cercle noir, où elle va rebrousser (mais sur le même support: le segment), ou au centre (deux fois, une dans chaque sens). Et voici l'énoncé par son auteur
Il y a essentiellement deux raisons, héritées de l'astronomie grecque:
Il insiste bien sur la nature de la trajectoire
Suit une démonstration rigoureuse. On peut se demander, en regardant le manuscrit, si les copistes ont lu ce qu'ils écrivaient avant de faire la figure! Ce qui amène Carra de Vaux à ajouter une note et refaire la figure:
Al-Tusi termine en montrant que son système correctif du déférent circulaire peut, plus généralement, s'appliquer aux autres planètes:
Malgré son ingéniosité, son système ne percera pas les caprices de Mercure. Pas plus que celui de Leverrier bien plus tard: une planète pertubatrice inconnue jusqu'alors (ce sera Neptune) expliquait les anomalies d'Uranus, pourquoi ne pas en imaginer une qui troublerait Mercure? Son nom était prêt, mais on ne la trouva jamais, et la longue résistance de Mercure ne devait être vaincue que par... la Relativité Générale d'Albert Einstein!

La figure du couple apparait clairement sur ce timbre.
(L'Azerbaïdjan considère aussi Al-Tusi comme un de ses illustres ressortissants)
Le couple d'Al-Tusi se retrouvera... dans le De Revolutionibus
de Copernic! Moins simplificateur que
mécaniquement
cohérent (c'est là la vraie Révolution
Copernicienne), le système de Copernic
ne supprimait pas les
épicycles, et ce fut d'ailleurs un handicap
supplémentaire pour son adoption. Même lemme,
mêmes
notations (ou presque): Copernic a-t-il eu accès
à
l'ouvrage d'Al-Tusi (mais par quel canal? ) ou a-t-il
réinventé le fameux lemme face à
la
nécessité (L'histoire des sciences abonde en
doubles
découvertes indépendantes)? La question est
encore
ouverte et la curiosité des historiens piquée;
elle
risque le demeurer longtemps si l'on ne découvre pas de
nouveaux
documents.
D'ailleurs, cette propriété sera encore retrouvée de nombreuses fois, par Jérôme Cardan (1501-1576) en 1570, puis par Philippe de La Hire (1640-1718), qui a étudié de façon plus approfondie les roulements d'une courbe sur une autre (Traité des Roulettes, 1706).. Et le lemme d'Al-Tusi se fond ainsi dans le. théorème de La-Hire, dont il n'est qu'un cas particulier.
(Aggrandissements sur le site
de philatélie mathématique de Jeff
Miller)
Le plus
intéressant se trouve,
bien sûr, sous le dôme: ce sont les restes du
cadran
géant. Les fondations, bien en
évidence, forment un cercle de 28m de diamètre.
Une image d'archive
montre l'aspect
du site avant qu'il n'ait été couvert. ;Le
bâtiment
avait 4 étages, compte tenu de la hauteur
nécessaire pour
loger le grand quadrant.
 |
 |
| photo ancienne (date inconnue): avant couverture | restitution en élévation |
| Source de ces images: blog de Parviz Tarikhi, physicien iranien. | |
On découvre
ensuite le plus
beau vestige, ce qui reste du quadrant et permet de se faire
une bonne
idée de sa taille: le rayon du cercle dépassait
18m!.
Ce quadrant est
aligné sur le
méridien du lieu, qui était à
l'époque,
pour l'empire d'Hulegu Kahn, ce qu'est pour le monde actuel le
méridien de Greenwich. Voici une maquette, plus ou moins
fidèle (sextant plutôt que quadrant, curieux
rapport des
distances: hauteur supérieure au
diamètre, ce qui
parait vraiment peu probable!). Du moins a-t-elle le mérite
de
concrétiser l'implantation d'un tel appareil dans une tour.
Source: Musée pour l'Histoire des
Sciences et Techniques en Pays d'Islam, Istanbul (Turquie)
Même en ruines, l'observatoire impressionnera et inspirera fondamentalement un visiteur et grand astronome : Ulugh-Beg lui-même, qui tracera les plans de l'observatoire de Samarcande à partir de ceux de Maragheh. Il inspirera aussi le rsouverain Moghol Jaï-Shing, qui fera construire, toujours sur ce modèle, l'observatoire de Jaïpur. Celui-ci, fort bien conservé (promis, le Mathouriste vous en reparlera plus longuement un jour prochain...), donne une idée de l'aspect imposant des instruments de Maragheh.et Samarcande.
Ce qu'on y fit
Avec qui, et avec quels moyens
Al-Tusi entouré de son équipe à l'observatoire de Maragheh
Source: blog de Parviz Tarikhi, physicien iranien.
Car tout cela avait un coût important: bâtiments, instruments, entretiens, salaires du personnel... Hulagu Kahn innova économiquement, en finançant tout cela grâce aux biens de main morte (ou waqf: en droit islamique, donation à perpétuité d'un particulier pour financer une œuvre d'utilité publique).
Des observations soignées
Pour faire de bonnes observations, il faut:- un ciel bien dégagé; il est d'une grande pureté dans l'Azerbaïdjan Iranien;
- des assistants sûrs qui se relaient aux postes d'observation nuit après nuit;
- de grands instruments (au moins en ce temps-là).
Outre le grnad quadrant méridien évoqué, voici le type d'instrument qui devait équiper les petites tours adjacentes ( repères 9 du plan):
 |
|
| Instrument 1 | Instrument 2 |
| Source: Musée pour l'Histoire des Sciences et Techniques en Pays d'Islam, Istanbul (Turquie) | |
L'instrument 1 est classique, on le trouvait déjà à Ravy ou Isfahan; Avicenne le décrit également. Le bras A peut tourner de 360° autour de l'axe de la tour, tandis que le bras B se meut dans le plan vertical de A (grâce à la coulisse C); la combinaison des deux permet de viser n'importe quel astre. mesure l'azimut de l'étoile, On mesure alors l'azimut avec A (observer que le haut de la tour est gradué) et la hauteur sur l'horizon avec B. Ces deux angles sont un peu moins familiers que les coordonnées longitude et latitude ne le sont aujourd"hui; pourtant il s'agit du même principe de coordonnées orthogonales sur une sphère, comme le petit tableau qui suit vous le rappelle.
| repérage absolu | repérage local (de l'observateur) | observations |
| équateur | horizon | grand cercle de la sphère |
| pôle Nord | zénith | sur la perpendiculaire élevée du centre au plan du grand cercle |
| méridien Greenwich | méridien du lieu | définit la mesure 0 pour les angles longitude et azimut |
| longitude | azimut | |
| latitude | hauteur |
Tout le génie de l'astrolabe consiste d'ailleurs à automatiser le passage d'un système de coordonnées sphériques à l'autre, en ayant aplati le tout en deux dimensions grâce à une projection bien chosie.
L'instrument 2 a été conçu par Al-Urdi pour cet observatoire; il permet de mesurer simultanément, selon le principe de l'instrument1, deux positions d'astres différentes (l'une avec le quart de cercle A, l'autre avec B) -sans doute pour conduire plus rapidement les calculs de comparaison. Ces quarts de cercles remplacent la coulisse C de .l'instrument 1; ils décrivent entièrement une hémisphère lorsque lon fait varier l'azimut. C'est moins rustique, plus précis, mais sans doute bien plus cher à la fabrication!
Le résultat fut la constitution des tables Ilkhanides (Zīj-i Īlkhānī), ainsi nommées en l'honneur de la dynastie d'Hulagu; de fait, elles ne furent publiées que sous le règne de son fils, en 1272. Soit quasi immédiatement après la réalisation du programme de 12 ans lancé à la mise en fonction! Leur qualité leur valut d'être traduite du Persan vers l'Arabe et d'être utilisée jusqu'au XVème siècle. La précession des équinoxes (page anglosaxonne beaucoup plus riche) calculée était de 51" d'arc par an;, la valeur établie aujourd'hui est de 50",2 et la précision de l'évalutaion de Maragheh reste saluée comme remarquable par toutes les histoires de l'astronomie.
| Source: Gallica BnF, tables d'Al-Tusi (disponibles en ligne) | |
Et du travail théorique
L'observation nocturne n'était pas, loin s'en faut, le seul travail qui s'y faisait. Il y avait de quoi s'occuper Night and Day: c'est là qu'ont été passés au crible les modèles théoriques de l'astronomie Ptoléméenne, qu'ils ont été critiqués, enfin qu'is ont été améliorés. La bibliothèque était réputée contenir 400000 ouvrages! Al-Tusi en a produit énormément lui-même: on dénombre 150 livres dont il est l'auteur, en comptant des ouvrages de morale, de religion.... sans qu'on connaisse exactement la répartition de ses écrits entre Alamut et Maragheh. Pour ce qui concerne les Mathématiques et l'Astronomie, il a notamment assuré la traduction en Persan ou en Arabe, assortie d'un travail de révision mathématique de nombreux classiques grecs, comme les Éléments d'Euclide, le Traité de la Mesure du Cercle d'Archimède (Taḥrīr al-Mutawassiṭāt) ou les Sphériques de Théodose de Bithynie. Et, bien sûr, l'Almageste de Ptolémée, la référence canonique de l'astronomie hellénistique.| Al-Tusi, Commentaire
sur le Traité de la Sphère et du Cylindre
d'Archimède (Tahrir
kitab al-kura wa'l-ustuwanal Arshimidis) Copie manuscrite,
XVème (vente Sotheby's)
|
Al-Tusi, Exposition des Éléments d'Euclide.Copie manuscrite, XVème (vente Sotheby's) | Al-Tusi, Commentaire
sur l'Almageste (Tahrir
al-Majisti) de
Ptolémée. Copie manuscrite, XIVème (vente Sotheby's) |
Célèbre pour... son couple!
En dépit de
ce titre quelque peu people,
ne croyez pas que l'on va vous parler de sa vie privée...
mais
plutôt d'une trouvaille qui l'a rendu
célèbre. Il
s'agit d'une idée géométrique
permettant
d'engendrer un mouvement
rectiligne à partir de deux
mouvements circulaires uniformes.
Il est assez facile de s'en faire une idée rien qu'en réfléchissant un petit peu. Avec un rayon r = R/4, la valve a fait un tour complet sur la roue en décrivant un quart de cercle seulement sur la piste. Comme elle reste à l'intérieur du grand cercle, elle rebrousse et décrit une trajectoire similaire, mais déduite par une rotation de 90°. Elle rebroussera donc 4 fois pour que tout le grand cercle soit décrit, et un stylo fixé à cette valve dessinerait sur le fond une sorte d'as de carreau: c'est la courbe que les mathématiciens nomment astroïde. Avec r = R/3, l'allure serait du même type, mais avec seulement 3 points de rebroussement, puisque la valve décrirait en un tour de roue le tiers de la piste: on l'appelle deltoïde (elle ressemble à la lettre grecque delta). Et toutes ces courbes sont des hypocycloïdes, parce qu'un cercle roume "sous" (dans) un cercle.
D'ailleurs... vous pouvez le tester vous-même, à l'aide du célèbre jouet Spirograph. Version "à l'ancienne", si vous en avez un dans votre grenier, ou contemporaine grâce à de nombreux sites Internet dédiés!
Le Mathouriste vous suggère de faire vos propres expériences sur celui-ci, qui est d'un emploi très simple: R et r ont la siginification que nous leur avons donnée; prenez enfin d = r ( plus généralement, on peut marquer sur la roue un point à une distance d du centre de la roue)
C'est très facile à prouver à partir des équations générales des hypocycloïdes, un plaisir qu'on laisse aux lecteurs avertis.
Les jeux sont faits, rien ne va plus... voici les résultats!
Un peu de mécanique (terre à terre) préalable...
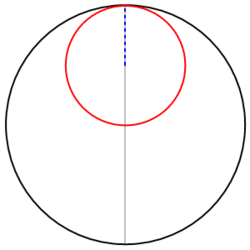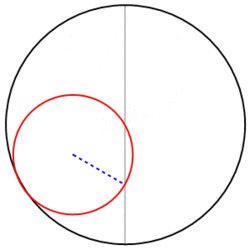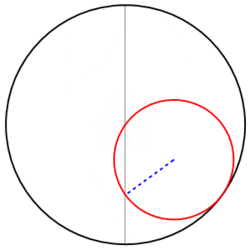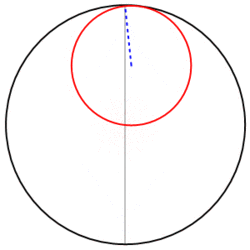
De façon générale, on peut poser le problème de mécanique suivant:| Une roue de vélo (son rayon sera nommé r) roule à l'intérieur d'un cercle de rayon R : quelle trajectoire suit la valve de la roue de vélo? |
Il est assez facile de s'en faire une idée rien qu'en réfléchissant un petit peu. Avec un rayon r = R/4, la valve a fait un tour complet sur la roue en décrivant un quart de cercle seulement sur la piste. Comme elle reste à l'intérieur du grand cercle, elle rebrousse et décrit une trajectoire similaire, mais déduite par une rotation de 90°. Elle rebroussera donc 4 fois pour que tout le grand cercle soit décrit, et un stylo fixé à cette valve dessinerait sur le fond une sorte d'as de carreau: c'est la courbe que les mathématiciens nomment astroïde. Avec r = R/3, l'allure serait du même type, mais avec seulement 3 points de rebroussement, puisque la valve décrirait en un tour de roue le tiers de la piste: on l'appelle deltoïde (elle ressemble à la lettre grecque delta). Et toutes ces courbes sont des hypocycloïdes, parce qu'un cercle roume "sous" (dans) un cercle.
D'ailleurs... vous pouvez le tester vous-même, à l'aide du célèbre jouet Spirograph. Version "à l'ancienne", si vous en avez un dans votre grenier, ou contemporaine grâce à de nombreux sites Internet dédiés!
Le Mathouriste vous suggère de faire vos propres expériences sur celui-ci, qui est d'un emploi très simple: R et r ont la siginification que nous leur avons donnée; prenez enfin d = r ( plus généralement, on peut marquer sur la roue un point à une distance d du centre de la roue)
Le célèbre lemme
Et maintenant, qu'adviendra-t-il si
r = d = R/2?
Raisonnons "avec les mains", comme disent les
mathématiciens. (Cela veut dire que vous donnez
une idée de la preuve, pas une
preuve au sens de la rigueur de la corporation. En gesticulant, en
quelque sorte, d'où l'expression!) . La courbe rebroussera
deux
fois seulement, aux extrémités du
diamètre, et va
garder des symétries par rapport au diamètre et
à
sa perpendiculaire, que
voulez-vous que ce soit d'autre qu'un segment? (C'est
là que la rigueur manque, bien sûr).C'est très facile à prouver à partir des équations générales des hypocycloïdes, un plaisir qu'on laisse aux lecteurs avertis.
Les jeux sont faits, rien ne va plus... voici les résultats!
 |
 |
| en animation: si une roue de vélo (rouge) tourne dans un cercle de rayon double (noir), la valve décrit un diamètre de ce cercle. | sur un manuscrit, Bibliothèque du Vatican |
| source commune des deux images: page Al-Tusi dans Wikipedia | |
Le manuscrit donne, à la manière d'une chronophotographie, les passages aux 4 instants qui divisent le temps de parcours sur le cercle noir en 4 intervalles égaux; la valve se trouve alors aux extrémités du diamètre du cercle noir, où elle va rebrousser (mais sur le même support: le segment), ou au centre (deux fois, une dans chaque sens). Et voici l'énoncé par son auteur
| "Lemme: deux cercles sont dans un même plan; le diamètre de l'un est la moitié du diamètre de l'autre; on les donne tangents intérieurement, et l'on donne un point sur le plus petit, le point de contact; puis on fait mouvoir ces deux cercles de mouvements réguliers, en sens opposés, tels que le mouvement du petit soit double du mouvement du grand; le petit accomplit deux tours pendant que le grand en accomplit un. On démontre que le point donné se meut sur le diamètre du grand cercle, qui passait au départ par le point de contact, allant et venant entre ses deux extrémités." |
Mais... pour quoi faire?
Tout cela peut légitimement paraître bien compliqué à qui n'est pas averti. Pourquoi se compliquer ainsi la vie?Il y a essentiellement deux raisons, héritées de l'astronomie grecque:
- La perfection (supposée) des mouvements des astres devait ne se faire que sur des cercles (la courbe parfaite par excellente, tous ses points étant équidistant du centre), avec des mouvements uniformes (à vitesse angulaire constante). Hélas, la complexité des trajectoires observées (Mars, par exemple, rétrogradait dans le ciel à certains moments ), qui avait valu aux planètes du nom poétique d'astres errants, avait conduit les théoriciens grecs, au moins depuis Apollonius de Pergé, à "empiler les mouvements circulaires": la planète décrit uniformément un cercle (l'épicycle: le préfixe épi signifie autour), dont le centre, lui même mobile sur un autre cercle, plus grand (le déférent), tourne autour de la terre à vitesse constante. Le mouvement combiné fait décrire à la planète une épicycloïde (famille proche de celles des hypocycloïdes déjà rencontrées,équations très ressemblantes). Et ceci n'était que le cas le plus simple, car il fallait parfois réitérer le dispositif pour affiner des corrections successives. La qualité mathématique prédictive de ce modèle pourtant sans justification physique vraisemblable ne devait voir son explication que beaucoup plus tard, avec la théorie des séries de Fourier (1807): comme on le disait alors joliment, ce modèle sauvait les phénomènes.
- Malgrè tout cela, Ptolémée avait dû introduire, afin de supprimer certains cercles qui compliquaient trop ses modèles, une sorte de tricherie, le point équant: le mouvement était uniforme... mais pas vis à vis du centre du déférent. Vis à vis d'un nouveau point, symétrique de la terre par rapport à ce centre. Au passage, la terre perdait son rôle de centre des mouvements uniformes des déférents! Bref, l'efficacité augmentait, mais d'épicycles en équant, la perfection théorique était... de moins en moins parfaite: que d'entorses et contorsions!
Al-Tusi entreprend, au
chapitre XI de
son Memento d'Astronomie, de s'attaquer à ces
problèmes.
Voici comment il commence son chapitre:
| "La première difficulté est celle qui a été mentionnée dans la théorie de la lune: il s'agit ici de celle qui consiste en ce que le centre du mouvement uniforme n'est ni au centre du monde, ni au centre du cercle déférent. Sur ce point, je n'ai rien reçu de ceux qui sont venus avant moi, et j'ai moi même inventé ce que je vais rapporter ici. Énonçons d'abord un lemme." |
et c'est là
qu'il
enchaîne sur l'énoncé posé
plus haut. Le
mécanisme précédent,
généralisé sans peine à des
sphères,
est incorporé dans un ensmble plus complexe de 4
sphères
tangentes (et pas seulement 2, comme dans le lemme).: le couple
d'al-Tusi est celui des sphères (3) et (4) de sa figure. Le
tout, qu'on peut lire in extenso avec le commentaire de M. Carra de
Vaux dans le livre de Paul Tannery, Recherches
sur l'Histoire de l'Astronomie Ancienne (pp
337-361), donne à la lune une
trajectoire cycloïdale plus complexe, mieux apte à
rendre
compte de son mouvement réel, qui a toujours
été
un souci pour les mathématiciens, même les
meilleurs:
Newton n'affirmait-il pas plus tard que c'était le seul
problème qui lui donnait mal à la tête?
| manuscrit: page et détail de la figure | figure corrigée par Carra de Vaux | |
| source: BnF, Figures du Ciel, catalogue de l'exposition 1998-99 | in P.
Tannery, Recherches sur l'Histoire de l'Astronomie ancienne |
|
Il insiste bien sur la nature de la trajectoire
| "Nous avons dit que la courbe décrite par le centre de l'épicycle ressemblait à un cercle. Cela ne veut pas dire qu'elle est un cercle, car elle n'en est pas réellement un. En effet, [...]." |
Suit une démonstration rigoureuse. On peut se demander, en regardant le manuscrit, si les copistes ont lu ce qu'ils écrivaient avant de faire la figure! Ce qui amène Carra de Vaux à ajouter une note et refaire la figure:
| "Nous
avons dû corriger cette figure, très incorrecte
dans le
manuscrit. [...] La ligne marquée d'un trait fort
représente la trajectoire du centre de
l'épicycle. Le
manuscrit la montre grossièrement figurée par un
cercle." |
Al-Tusi termine en montrant que son système correctif du déférent circulaire peut, plus généralement, s'appliquer aux autres planètes:
| "C'est
là ce qui
m'appartient en propre sur ce sujet. Cette combinaison n'exige que
trois sphères de plus que l'on en compte ordinairement. [...] La même méthode peut être appliquée aux planètes supérieures et à Vénus. [...]Les difficultés sont donc résolues en ce qui concerne ces planètes par l'addition de trois sphères pour chacune d'elles, [...] Je n'ai pas ici la place de décrire convenablement le système que j'ai imaginé pour Mercure. Il faut une démonstration étendue pour expliquer le mouvement uniforme, autour d'un point, d'un ensemble de corps qui s'en rapprochent et s'en éloignent par l'effet de combinaisons compliquées. S'il plaît à Dieu, j'ajouterai cette théorie en appendice au présent chapitre." |
Malgré son ingéniosité, son système ne percera pas les caprices de Mercure. Pas plus que celui de Leverrier bien plus tard: une planète pertubatrice inconnue jusqu'alors (ce sera Neptune) expliquait les anomalies d'Uranus, pourquoi ne pas en imaginer une qui troublerait Mercure? Son nom était prêt, mais on ne la trouva jamais, et la longue résistance de Mercure ne devait être vaincue que par... la Relativité Générale d'Albert Einstein!
Et quelle postérité?
La figure du couple apparait clairement sur ce timbre.
(L'Azerbaïdjan considère aussi Al-Tusi comme un de ses illustres ressortissants)
D'ailleurs, cette propriété sera encore retrouvée de nombreuses fois, par Jérôme Cardan (1501-1576) en 1570, puis par Philippe de La Hire (1640-1718), qui a étudié de façon plus approfondie les roulements d'une courbe sur une autre (Traité des Roulettes, 1706).. Et le lemme d'Al-Tusi se fond ainsi dans le. théorème de La-Hire, dont il n'est qu'un cas particulier.
Plus insolite, Kelvin l'évoque
comme possibilté naturelle d'engendrer le mouvement oscillatoire
harmonique à partir d'un mouvement circulaire uniforme,
lorsqu'il présente sa machine à prédire les marées. Si le contexte est différent, c'est bien la même fonctionnalité mathématique que chez Copernic qui est recherchée: obtenir les
composantes harmoniques du mouvement qu'il n'y aura plus qu'à
sommer. Il est en effet important de souligner que l'usage qu'en font
Al-Tusi et Copernic est une forme primitive... de développement de Fourier!
Un dernier hommage
L'Iran a publié en 1974 un triptyque de timbres commémorant le septième centenaire du décès d'Al-Tusi (Noter que les deux langues utilisées sont le Persan et le Français!). L'illustration choisie est quelque peu énigmatique: le monument représenté, à n'en point douter, est le Gonbad-e-Sorkh (dit aussi: Tombeau Rouge) de Maragheh. On aurait pu s'attendre à une évocation de l'observatoire, alors qu'on est en présence du plus ancien tombeau monumental de la ville, édifié en 1147, vraisemblablement pour un prince kurde de la dynastie d'Ahmadi, dirigeant d'un petit royaume. Quel rapport avec Al-Tusi? Il se pourrait qu'il ait été autrefois pris pour sa sépulture, avant d'être plus correctement daté.
 |
||
| timbre 3 | timbre 2 | timbre 1 |
Un
site Internet le mentionne comme partie de l'Observatoire de Maragheh:
c'est également étonnant, puisque sa construction est
antérieure, et que le but en était
différent. Il
ne faut pas en déduire trop vite qu'il s'agit d'une erreur:
l'orientation astronomique soignée des monuments est une
longue
tradition qui remonte à la préhistoire
(Stonehenge,
Angleterre), traverse l'antiquité (Abu Simbel, Egypte) et
marque
les églises chrétiennes, et bien sûr
les
mosquées en terre d'Islam. Or, Cassini
donnera le magnifique exemple d'utilisation a posteriori d'une
église (la cathédrale de Bologne,
bientôt dans nos
pages!) comme observatoire... Néanmoins, par
élémentaire souci de rigueur scientifique et
historique, le
Mathouriste aimerait
trouver des sources d'information plus complètes sur ce
point,
et sur le choix de ce tombeau pour honorer Al-Tusi par ce timbre.
Références de l'épisode:
Livres:
- J.L.E. DREYER, A History of Astronomy from Thales to Kepler (Dover)
- R. RASHED & alias, Histoire des Sciences Arabes, t1: Astronomie, Théorique et Appliquée (Seuil)
- P. TANNERY, Recherches sur l'Histoire de l'Astronomie Ancienne (Gabay). Disponible en ligne sur Gallica.
- J.P. VERDET, Une Histoire de l' Astronomie (Seuil, points Sciences)
Articles en ligne
- P. TARIKHI, Maragheh: Heaven’s Gate (sur son blog)
- P. TARIKHI, Maragheh the biggest observatory of Middle Age, édition Internet de The Independant (02/04/2008)
- N. SIDOLI, T. KUSUBA, Nasir al-Din Al Tusi's revision of Theodosius 'Spherics'
-
E. VAN LIT, "The Measurement of the Circle” of Archimedes in Nasir al-Din Al
Tusi's revision of the 'Middle Books'
(Université d'Utrecht)
Sites:
- Hypocycloïdes et épicycloïdes sur le site de Robert FERREOL
- Déférents & épicycles sur Wikipedia
- Musée d'Histoire des Sciences et Techniques d'Istanbul (Islam Bilim ve Teknoloji Tarihi Müzesi)
Pour poursuivre dans nos pages...
Aller à l' Épisode
I : le Prisonnier d'Alamut
Revenir
à la Home
Page du
Mathouriste
