Dans la Chaleur des Séries...

... Une Promenade Fouriériste! (Partie 1)

Nous proposons au lecteur, dans cette page, de vivre "en direct" la naissance des séries de Fourier dans la Théorie Analytique de la Chaleur et certains manuscrits préparatoires de Fourier.
Il trouvera, à la fin de celle-ci, le chemin pour poursuivre la promenade dans ce merveilleux ouvrage...

La Chaleur, un Problème au Cœur de l'Époque

"Les physiciens sont partagés sur la nature de la chaleur. Plusieurs d'entre eux la regardent comme un fluide répandu dans toute la nature, et dont les corps sont plus ou moins pénétrés, à raison de leur température et de leur disosition à le retenir; [...]

D'autres physiciens pensent que la chaleur.n'est que le résultat des mouvements insensibles des molécules de la matière."



A.-L. Lavoisier, P.-S. Laplace, Mémoire sur la Chaleur
 in Mémoires de l'Académie des Sciences (1780)
Jacques-Louis David:
Lavoisier et son épouse .
Metropolitan Musem of Arts, New-York
 Pierre Simon Laplace
E.N.S. rue d'Ulm (Paris)
façade sur la cour "aux Ernests"

Le débat est vif, les participants sont nombreux, mais il ne sera tranché que bien plus tard, avec Sadi Carnot et la naissance de la thermodynamique, puis Ludwig Boltzmann. Y mettre son grain de sel, c'est risquer s'enliser... Fort intelligemment, dès les premiers mots de l'introduction de son livre, Fourier se place au dessus de la mêlée, ou plus exactement à côté, comme le faisait déjà, un peu avant lui,  Rumford. Et réenfonce le clou dès le premier chapitre:

"Sans entrer dans des recherches arbitraires et difficiles concernant la nature du feu, à l'exemple des physiciens anciens et modernes qui, à cet égard ont toujours été d'opinions diffférentes, sans entreprendre de déterminer s'il existe un fluide igné, ou s'il n'y en a pas, [...]ou si la chaleur ne provient que d'une augmentation de mouvement dans les parties de corps chauffé [...]; en un mot sans m'enfoncer avec le lecteur dans un labyrinthe de ténèbres et d'incertitudes, je bornerai mes études à des objets plus utiles[...]: de la manière la plus avantageuse de la produire, et de la diriger avec certitude et efficacité dans les différents procédés utilisés pour l'économie domestique."
Rumford, An Inquiry Concerning the Weight Ascribed to Heat (1799)
"Les causes primordiales ne nous sont point connues; mais elles sont assujetties à des lois simples et constantes, que l'on peut découvrir par l'observation, et dont l'étude est l'objet de la philosophie naturelle.
La chaleur pénètre, comme la gravité, toutes les substances de l'univers, ses rayons occupent toutes les parties de l'espace. Le but de notre ouvrage est d'exposer les lois mathématiques que suit cet élément. Cette théorie formera désormais une des branches les plus importantes de la physique générale."
Fourier, Discours Préliminaire à la Théorie Analytique de la Chaleur (1822)
"On ne pourrait former que des hypothèses incertaines sur la nature de la chaleur, mais la connaissance des lois mathématiques auxquelles ses effets sont assujettis est indépendante de toute hypothèse; elle exige seulement l'examen attentif  des faits principaux que les observations communes ont indiqués, et qui ont été confirmés par des expériences précises."
Fourier, Théorie Analytique de la Chaleur, ch I, sect. 2 ( 1822, texte écrit dès 1811)

Pour confirmer expérimentalement, il faut choisir des grandeurs que l'on peut mesurer:
"La question de la propagation de la chaleur consiste à déterminer quelle est la température de chaque point d'un corps, à un instant donné, en supposant que les températures initiales sont connues."
Fourier, Théorie Analytique de la Chaleur, ch I, sect. 1 ( 1822)

Le Plan de FOURIER 

Mathématiquement, quelle équation va caractériser cette évolution? Comme il y a au moins deux variables (une de temps, et une d'espace au moins, par exemple dans une tige rectiligne), ce ne peut être qu'une équation aux dérivées partielles. L'objet est assez nouveau à l'époque: tout au plus a-t-on résolu la plus simple d'entre elles, l'équation des cordes vibrantes. Tellement nouveau que Fourier emploie encore  l'expression équation différentielle, réservée aujourd'hui au cas d'une seule variable. Dès le Discours Préliminaire, Fourier se pose à la fois en mathématicien, en insistant sur la rigueur (il est certain qu'il a "mal digéré" les critiques à son mémoire de 1811!) et sur la construction d'un problème débarrassé de sa gangue physique, mais aussi en physicien, soucieux d'unmodèle maniable numériquement. Cette dualité ne va jamais le quitter tout au long de son travail et justifie qu'on voie en lui le père de la Physique Mathématique.
 
"Les équations différentielles de la propagation de la chaleur expriment les conditions les plus générales, et ramènent les questions physiques à des problèmes d'analyse pure, ce qui est proprement l'objet de la théorie. Elles ne sont pas moins rigoureusement démontrées que les équations générales de l'équilibre et du mouvement. [...]
Les équations du mouvement de la chaleur, comme celles qui expriment les vibrations des corps sonores, ou les dernières oscillations des liquides, appartiennent à une des branches de la science du calcul les plus récemment découvertes, et qu'il importait de perfectionner. Après avoir établi ces équations différentielles, il fallait en obtenir les intégrales; ce qui consiste à passer d'une expression commune à une solution propre assujettie à toutes les conditions données.  Cette recherche difficile exigeait une analyse spéciale, fondée sur des théorèmes nouveaux  [...]. La méthode qui en dérive ne laisse rien de vague et d'indéterminé dans les solutions; elle les conduit jusqu'aux dernières applications numériques, condition nécessaire de toute recherche, et sans laquelle on n'arriverait qu'à des transformations inutiles. "
Fourier, Discours Préliminaire à la Théorie Analytique de la Chaleur (1822)

 Voici, dans un manuscrit antérieur à la rédaction définitive, la première apparition de l'équation aux dérivées (Fourier dit: "différences") partielles, obtenue en effectuant un bilan thermique dans un volume élémentaire: sont présentés un cas unidimensionnel et un cas bidimensionnel.

Source du manuscrit: BnF

Dans le traité de 1822 apparait la stratégie qu'annonce le discours préliminaire: le problème, plutôt qu'être abordé dans le cas général, est posé dans des cas successifs à la géométrie remarquable, section par section, dans le chapitre II. Il sera ensuite résolu dans le même ordre, chapitre par chapitre, ce que résume le tableau de correspondance ci-dessous. Cette progressivité est typique de la manière de l'auteur.


 lame armille sphère cylindre prisme cube  qq
Position, section
II.1 II.2 II.3 II.4 II.5 II.6
Résolution, chapitre III IV V VI VII VIII IX

Le problème se présente, dans tous les cas, sous la forme suivante, qui fait intervenir l'opérateur laplacien à 1,2 ou 3 variables d'espace, selon le cas:

 
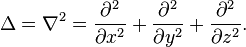
évolution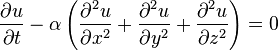
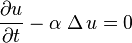donnée au bord u (P; t) = φ (P) φ donnée
P point du bord
condition initale u (x, y, z ;0) = ψ (x, y, z) ψ donnée

La Méthode de FOURIER: Séparer pour Régner!

Un cas ultra-simple: la lame à l'équilibre thermique

Suivant sa logique de gradation dans la complexité, Fourier va commencer par un cas où le temps n'intervient pas: la dérivée par rapport à t est donc nulle. C'est le régime stationnaire: il s'agit de calculer la répartition des tempréatures quand l'équilibre thermique est atteint, étant données les températures au bord.
De plus, la géométrie du domaine est la plus simple possible: un rectangle infini à droite, des températures constantes sur ses trois bords, parce que c'est aisément réalisable pour la confrontation expérimentale.

Source du manuscrit: BnF
"Ainsi la question actuelle consiste à déterminer les températures permanentes d'un solide rectangulaire infini, compris entre deux masses de glace B et C et une masse d'eau bouillante A; la considération des questions simples et primordiales est un des moyens les plus certains de découvrir les lois des phénomènes naturels, et nous voyons, par l'histoire des sciences, que toutes les théories se sont formées suivant cette méthode."
Fourier, Théorie Analytique de la Chaleur, ch III, § 164 ( 1822)
Là, on sent le mathématicien: les valeurs des températures sont "idéalisées" à 0 et 1, pas 0 et 100!
Noter également comment il défend sa méthode face au jugement de l'histoire (des sciences).


Qu'est devenu le problème complet, dans ce cas?
Moyennant un choix de reprère naturel,en voici les équations (à l'équilibre, la condition initiale n'a plus d'importance)


évolution Δ u = 0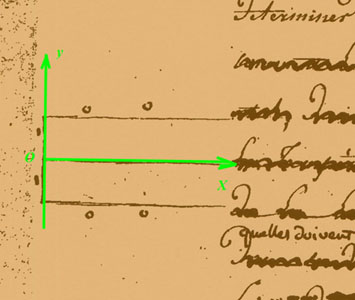
donnée au bord
(horizontal)		 u (x,  π/2 ) = 0
u (x, -π/2 ) = 0
donnée au bord
(vertical)		 u (0, y) = 1

Solutions à variables séparées

L'équation aux dérivées partielles s'est donc simplifiée: il reste une équation de Laplace, Δ u = 0. Sauf qu'elle n'est pas plus facile à intégrer!
Mais, deuxième application de son principe: "faisons des choses simples d'abord", Fourier va rechercher des solutions dont les variables coordonnées x et y interviennet "séparément" (d'où le nom de méthode de séparation des variables), c'est à dire de la forme produit de deux fonctions séparées, l'une de x, l'autre de y (comme il n'y a que 2 variables, Fourier a repris la lettre z pour la fonction inconnue)
z (x, y) = φ(x).ψ(y)



Noter l'écriture "d'époque" φx au lieu de φ(x)  (Source du manuscrit: BnF)
Cela peut paraître à la fois incroyablement restricitf et dangereusement arbitraire.
Restrictif ? Pas tant que cela, car l'auteur ne va pas en rester là: il va les combiner pour construire des solutions bien plus complexes. Un peu comme un chimiste (et la vie, tout simplement!) est capable d'élaborer des molécules très compliquées à partir des éléments C, H, O...
Arbitraire? Certes, rien ne garantit le résultat: en particularisant trop, on court le risque de laisser échapper des solutions (De fait, on sait aujourd'hui que cette technique ne donne pas des résultats à tout coup). Mais si le choix est : demeurer à l'arrêt, en gémissant que le problème est trop dur, ou tenter cette voie en se disant que si ça réussit, c'est 100% de gagné... le pragmatisme du physicien parle: qui ne tente rien n'a rien. L'attitude ne diffère en rien de celle d'un autre géant "mathématicien physicien", qui, face au problème des 3 corps en mécanique céleste (un problème dont justement, on ne peut exhiber toutes les solutions) dira de certaines solutions particulières

"D’ailleurs ce qui nous rend ces solutions périodiques si précieuses, c’est qu’elles sont, pour ainsi dire, la seule brèche par où nous puissions essayer de pénétrer dans une place jusqu’ici réputée inabordable."
Henri Poincaré, les Méthodes Nouvelles de la Mécanique Céleste, t1, ch III, 1892

C'est un pari, mais il va s'avérer gagnant et extraordinairement fructueux. Le mathématicien, qui n'aime rien tant que le rôle du Schtroumpf grognon, pourrait encore objecter:
 "Une solution, soit! Mais qui vous dit qu'il n'y en a pas d'autre?"
Allons, bon! Nous manquions de solutions, risquerions nous d'en avoir trop... et donc que celle de Fourier ne soit pas la bonne? C'est poser la question de l'unicité. Fourier n'y viendra que plus loin, sans doute parce qu'elle est "physiquement évidente": comment imaginer que, bien déterminée aux bords, la température puisse "tirer au sort" sa répartition entre diverses possibilités? Cela va à l'encontre du credo du Déterminisme Laplacien: répétée avec les mêmes conditons de départ, une expérience de physique doit retourner les mêmes solutions.
Quand Fourier la traitera, ce sera en usant de la linéarité de l'équation: la différence de deux solutions est encore solution; dès lors elle vaudrait partout 0 au bord (1-1 sur le bord "chaud" de la lame). Donc (pas plus prouvé, mais l'imtime conviction en est encore physiquement plus forte), la temrérature ne peut qu'être nulle partout, et les deux solutions sont égales!

Il est grand temps de résoudre ces équations à coefficients constants:
  • fixant y = y0,  φ vérifie  φ"(x) - λ φ(x) = 0; λ est une constante;
  • fixant x = x0,  ψ vérifie  ψ"(y) -ν ψ(y) =  0; ν est une constante;
  • fixant x = x0 ET  y = y0,  ν = - λ 
et de reformuler le problème en traduisant les conditions au bord:

φ"(x) - λ φ(x) =0 ψ"(y) + λ ψ(y) =0

ψ(- π/2) = ψ( π/2) =0

Un peu péremptoirement (au vu de nos canons de rigueur contemporains), Fourier pose  λ = m² et tire les solutions qui l'intéressent... D'abord, rappelons qu'il en a le droit: il lui suffit de trouver de quoi construire une solution! Et il justifie ses choix a posteriori: décroissance de la chaleur, contrainte des valeurs aux limites sur les bords de la lame.
Source : BnF
Conseillons tout de même à un étudiant (de prépa, par exemple) de traiter l'exercice avec un peu plus de scrupules et de méthode, pour vérifier que seules les λn= (2n+1)² sont "utiles".
[ indication: commencer plutôt par l'équation en ψ, beaucoup plus contraignante...]
Mine de rien, Fourier vient d'introduire les valeurs propres du problème: comme une corde ne pouvait vibrer librement que selon certains modes propres (propres à la corde, d'où l'appellation), le régime des températures "propres" de la lame glacée au bord fait appel à une famille dénombrable seulement de valeurs.

Sommer pour de nouvelles solutions: un peu, beaucoup, passionnément!


Source : BnF

L'équation, on l'a dit, est linéaire: toute somme, toute combinaison  linéaire de solutions est encore solution. Cela va considérablement augmenter le répertoire...
Seulement, si l'argument est parfait pour une somme finie (aussi nombreux soient les termes), il ne s'applique pas sans précaution à une somme infinie, ce qu'on appelle une série. Ces questions délicates ne seront élucidées que plus de 50 ans après, par Weierstrass (Convergence uniforme, 1871); à l'époque de Fourier, l'influence dominante est encore celle d'Euler, où tous les coups sont permis... pourvu qu'ils soient fructueux.
Précisons qu'en l'espèce, avec des coefficients bornés (un résultat immédiat quand on connait les formules... auxquelles va bientôt arriver Fourier!) cest un jeu de Taupin (si pas tout à fait un jeu d'enfant...) de légitimer la dérivation terme à terme de la série.

Acte de Naissance de la Première Série de FOURIER

Réussir une Première...

Mais une somme finie ne sera guère utile, car il reste une condition à satisfaire: la valeur 1 au bord gauche de la lame! Exemple avec une somme à 4 termes:

u (x, y) =  a e -xcos y + b e -3xcos 3y + c e -5xcos 5y + d e -7xcos 7y
1 = u (0, y) =  a cos y + b  cos 3y + c cos 5y + d cos 7y

Réaliser l'égalité pour tout y de ]-π/2, π/2[ est impossible.

Reste donc à essayer une série, puisqu'il n'y a pas le choix...

Voilà donc Fourier au pied du mur:
il faut développer 1 comme série trigonométrique.
Source : BnF
Et s'il ménage le suspense, c'est surtout parce qu'il doit être au courant des controverses qui ont agité d'Alembert, Euler et Daniel Bernoulli à ce sujet, un demi-siècle auparavant. 

Il faut maintenant s'atteler au calcul des coefficients.
Pour ce premier exemple, l'itinéraire suivi est périlleux, plein d'affirmations non justifiées, voire non justifiables. Mais qu'importe! Il s'agit de découvrir le résultat, tant pis si  la voie est dangereuse: on pourrait la comparer à celle qu'ont emprunté en 1786 Paccard et Balmat à l'assaut victorieux du Mont-Blanc: la charte de la Compagnie des Guides en interdit l'usage (au point que la reconstitution nocturne avec torches du bicentenaire était inexacte sur une centaine de mètres de dénivelé), il y a aujourd'hui un itinéraire plus sûr. De même pour les coefficients de Fourier, encore fallait-il passer une première fois.
Fourier part de l'égalité (dont il n'est même pas sûr qu'elle tienne!)
1 = a cos y + b  cos 3y + c cos 5y + d cos 7y + ...
et la dérive indéfiniment par rapport à y, avant de faire dans chaqua ligne y = 0. Cette fois, il y a de quoi brandir le carton rouge: les séries dérivées successives sont divergentes! Cela lui fournit un système d'une infinité d'équations à une infinité d'inconnues. 
On ne sait pas davantage résoudre cela; alors, pour travailler sur quelque chose de plus simple, il considère les systèmes carrés successifs obtenus par troncatures, en gardant n équations et n inconnues. Pour n=3, ce serait
1 = a +     b +     c 
0 = a + 32 b + 52c
0 = a + 34 b + 54c
On peut calculer le a de ce système: c'est en fait un a(3). Avec n=4, on obtiendrait un a(4) différent, et très généralement un a(n) . Fourier affirme que le "vrai" a, solution du système infini, est la limite de ces a(n), et qu'il en ira de même pour les coefficients suivants! Cela peut certes sembler intuitif, mais l'affirmation reste donnée comme allant de soi, sans justification supplémentaire. Tout en présentant encore ce calcul, par souci historique probablement, Lebesgue met nettement en garde le lecteur... mais, dans le fond, n'est-ce pas mieux que de laisser croire que tout était parfait dans le meilleur des ouvrages de mathématiques, que rien n'avait dû être repris depuis la découverte?

"Ce mode de résolution prête à bien des objections; d'abord il n'est pas évident que la limite des a(n) soit une solution, puis il n'est pas évident que ce soit la seule solution. [...] Il paraît d'ailleurs bien difficile  [...] de rendre rigoureux le procédé qu'emploie Fourier pour déterminer les a,b,c,... ; pour le cas simple où f = x, ce qui est le premier des exemples de Fourier, les séries qui figurent dans les équations sont divergentes."
Henri Lebesgue, Leçons sur les Séries Trigonométriques (1906)




Deux manuscrits: début et fin du calcul du coefficient a.
(Source: BnF)		 Un "sauveur" nommé John Wallis!

La fortune, dit on, sourit aux audacieux: la règle générale de formation des  a(n) apparait clairement (Théorie Analytique, ch III, sect. 2), et au bout, un signe des Dieux de l'Olympe mathématique: la célèbre formule de Wallis lui donne immédiatement a = 4/π . C'est trop beau pour être faux! Les autres coefficients s'expriment de façon similaire. Fourier a dû aimer l'esthétique de ce calcul, car il l'a maintenu dans l'édition de 1822, alors qu'il savait le faire "plus simplement" après coup. Valeur de la démarche de recherche, qu'il ne cherche pas à gommer, mais à mettre en lumière: l'écriture est aux antipodes des Éléments d'Euclide... ou de Bourbaki.


Source : BnF		 Voici  donc Fourier en possession de son développement. Avec beaucoup de précision, il en donne la validité, soulignant qu''on développe ainsi, non une constante, mais une fonction créneau, et il évoque sa convergence. Mais s'il donne pour cela une définition impeccable (D) ... il ne s'attarde pas et "laisse au lecteur" le soin de s'en occuper. Or ce n'est pas si facile: la preuve directe de la convergence -i.e. indépendamment de sa valeur requiert une méthode plutôt fine, la transformation d'Abel.

Il semble alors revenir à son objet, car il ne faut pas oublier un point essentiel:  le développement trigonométrique n'était pas une fin en soi, mais le moyen d'accéder aux coefficients de la solution du problème de la chaleur dans la lame.
On attendrait à ce moment de tout "vrai physicien" la récapitulation de la solution, pour laquelle il a maintenant tous les éléments en main...

Mais le mathématicien Fourier n'est pas décidé à finir sa promenade sans cueillir les jolies framboise au bord du chemin!
En l'occurrence, retrouver quelques sommes de séries qu'Euler a semées au long de son Introduction à l'Analyse Infinitésimale, que Fourier connaît bien, visiblement.
Dont la réponse au célèbre problème de Bâle: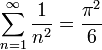

 sur lequel avaient séché Leibniz et les Bernoulli, mais qu'Euler avait résolu avec une maestria culotée (en traitant respectivement une série entière et un produit infini comme un polynôme et le produit de ses facteurs: voir ici sa solution)

Fourier commence par intégrer sa série terme à terme... calcul conduit à la Euler, de façon purement formelle.
Puis, faisant  x = π/2, il obtient la solution.

Exercice pour le temps présent (et lecteur averti):
justifier l'intégration faite par Fourier!
  • Méthode 1 : 
    • convergence uniforme sur [0,α], α <  π/2 ( encore Abel!)
    • intégration sur cet intervalle
    • limite, en faisant tendre  α vers π/2
  • Méthode 2 : 
    • utiliser un théorème de Lebesgue pour les séries
NB: il existe des méthodes plus élémentaires, ne serait-ce qu'en manipulant sommes finies de sinus ou cosinus  et restes -ce qui évite les manipulations de séries.

Source : BnF

Et revenir à la Physique!

Voici enfin, au §190, la récapitulation attendue: la série vérifie l'équation aux dérivées partielles (grâce à une dérivation terme à terme de la somme, non justifiée certes, mais aisément justifiable, on l'a dit plus haut) et les conditions aux limites, aux bords. Et quand le mathématicien a fini ce travail, il n'oublie pas le physicien qu'il est aussi, en remarquant que, grâce aux exponentielles, la convergence très rapide permet un calcul simple, avec trois termes au plus (§191): de quoi confronter facilement aux résultats expérimentaux.
On peut aussi comprendre que, si du point de vue pratique numérique la série se résume à trois termes, la question de la dérivation terme à terme ne soit pas mathématiquement brûlante: pour une somme de 3 (ou de 100, ou de 47683 termes), la simple linéarité de l'équation y pourvoit: le principe de superposition s'applique à toute somme finie.


Montage photographique des § 190, 191 afin d'éviter les sauts de page inopportuns. (Source : Théorie Analytique, BnF)

Ainsi, dans ce cas très simple, le programme mathématico-physique est parfaitement tenu. Reste, les bases de la méthode étant jetées, à élargir le champ d'action, d'abord en modifiant la répartition de température au bord gauche, puis en introduisant le temps et d'autres domaines.

Développement d'une fonction "quelconque"

 De l'Audace, encore de l'Audace, toujours de l'Audace!
Extraits du § 207. (Source : Théorie Analytique, BnF)

S'il martèle dès le départ les mots "arbitraire", "quelconque", Fourier semble nous prendre à contrepied: la fonction qu'il considère est (tout à fait implicitement) supposée développable en série entière! De nouveau, nous voilà plongés dans le style typique de Fourier, celui que nous avons comparé à la "méthode Paccard-Balmat", celui qui a fait école chez les mathématiciens du monde entier (si vous en doutez, lisez le délicieux petit ouvrage de George Polya, How to Solve it? [disponible en ligne]: pouvez vous résoudre un problème plus facile? Avec des hypothèses renforcées?). Quand on aura découvert, on pourra effacer (à l'instar d'Euclide) les traces de la recherche, et faire autrement? Ou les laisser subsister, pour que le lecteur partage le cheminement de votre pensée, et c'est le choix de Fourier.
φ(x) est développé, d'une part en série entière, de l'autre en série trigonométrique, dont chacun des termes est à son tour développé en série entière: une interversion de la double somme lui donne un deuxième développement en série entière; il peut donc identifier les coefficients, et obtenir un système similaire au premier cas traité: seuls changent les seconds membres, qui, au lieu de 1,0,0,... sont les A, B, C, ... et donc, Fourier a pleine confiance en sa capacité à le résoudre.


Le calcul est quand même loin d'être trivial: il exige beaucoup de soin (les expressions manipulées sont plus grosses), une certaines virtuosité même quand il nécessite le calcul auxiliaire des séries d'inverses des puissances paires d'entiers: on reconnait le problème de Bâle pour les carrés, évoqué plus haut, généralisé aux puissances 4,6, ... et que croyez vous que fasse Fourier? Il connait son Euler, et suit les principes de sa solution du problème de Bâle, en comparant le développement en série entière usuel du sinus à celui qu'il peut tirer du produit infini d'Euler!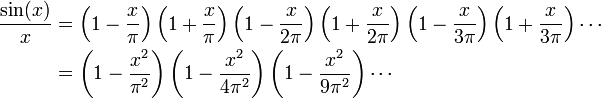

On observera que celui-ci exprime le sinus en fonctions de ses zéros, exactement comme le fait un polynôme dans le cas d'un produit fini; Fourier n'est donc pas dépaysé: n'est-ce pas ce qu'il fait depuis le début avec les séries?


(Source de l'image : Théorie Analytique, BnF)
Fourier obtient, au bout de ce (long) calcul, le coefficient de sin nx comme une série, faisant intervenir les dérivées successives en π (chacune est arrivée fort à propos pour "condenser" une série), Et voilà que notre bandit dérive... oui, vous lisez bien si vous avez aggrandi: par rapport à π!
Bon, pas de panique: on pourrait considérer les mêmes expressions avec une variable t à la place de π. D'ailleurs, si vous aimez les brigandages eulériens, il en reste encore à vous mettre sous la dent! Il dérive cette expression s(t) terme à terme, avec les mêmes justifications que d'habitude... c'est à dire aucune, vous vous en doutiez. Mais cela lui permet de trouver une équation différentielle à coefficients constants vérifiée par s(t), l'intégrer par variation des constantes (le procédé classique). Il n'y a plus qu'à refaire t = π pour trouver enfin (expression encerclée en vert) la formule intégrale du n-ième coefficient sinus.

Extraits du § 219: dans l'expression du texte S( fx.dx), S désigne évidemment l'intégrale. (Source : Théorie Analytique, BnF)

232 pages après le début du traité, 74 pages après celui du chapitre III, un coefficient de Fourier est écrit sous sa forme intégrale!

"La méthode de Fourier est intéressante surtout à cause de l'ingéniosité des transformations qu'effectue Fourier."
Henri Lebesgue, Leçons sur les Séries Trigonométriques (1906)

Et Fourier de "justifier" qu'une telle formule est applicable à une fonction quelconque, en donnant le procédé graphique de construction (faire le produit, point par point) de la courbe sous laquelle il y a évidemment une aire, qui sera le coefficient intégral de Fourier.
Une "évidence" qui aura une riche postérité: dans sa thèse sur les séries trigonométriques (1851), Riemann se demandera :
"Et d'abord, que faut-il entendre par  ?"
avant de donner sa théorie personnelle de l'intégrale en moins de deux pages.

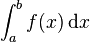 Enfin, les coefficients de Fourier!

Maintenant que l'intégrale de  φ(x).sin nx est démasquée, maintenant seulement il est naturel de repartir de cette expression, directement. Bien sur, il y aura encore une interversion série-intégrale injustifiée (pour nos yeux contemporains), mais sans état d'ême dans l'esprit eulérien (intégrale d'une somme, finie ou non, la différence nest pas perçue...). Au fil du texte, l'intégrale est toujours repérée par la lettre S (comme Somme). On notera aussi que, pour la première fois dans son texte, Fourier fait usage d'indices pour les coefficients.

Source : BnF

Une fois l'échange fait, il n'ya plus que le classique calcul par linéarisation du produit, en distinguant les deux cas selon l'égalité ou non des indices: le petit exercice que tout étudiant qui sait bien son cours doit pratiquer sans difficulté!

On parle aujourd'hui de relations d'orthogonalité, pour un produit scalaire intégral: cela allège bien agréablement les notations que d'écrire
<sin i. , sin j. > = 0
mais cette vision géométrique n'arrivera que plus tard, avec Hilbert!



Plus loin, Fourier effectuera le même travail avec une série de cosinus, puis mélangera les deux.

 Source de l'image: BnF


Il faudra attendre une bonne vingtaine de pages, pour que'au fil des exemples, Fourier introduise enfin, pour la première fois dans la communauté mathématique, le signe intégrale avec bornes; il l'assortit des classiques remarques sur les réductions par symétrie ou l'invariance par translation des coefficients.

Il faut croire que, d'emblée, cette notation parut combler un manque, car on la voit adoptée chez Cauchy -qui n'aimait guère que l'on eût inventé quelque chose avant lui- ou chez son vieux rival Poisson.


(Source de l'image : Théorie Analytique, BnF)

Donner plusieurs exemples est, à ce stade, très important: il s'agit de démontrer (au sens "commercial" du terme!) la maniabilité de ses séries, la facilité du calcul des coefficients, l'universalité dans le vaste champ des fonctions à étudier. Aussi choisit-il comme premier exemple celui qu'il a considéré 60 pages plus tôt ("Voyez comme son traitement est aisé!") et en second un cas... provocant: développer cos x en série de sinus! Ironie cruelle, c'est l'un des points qui avaient beaucoup chiffonné Lagrange, peut-être une des origines des reproches sur la rigueur faits à Fourier, alors que nous savons aujourd'hui qu'il n'y a rien à y redire, et que...c'est un exercice toujours donné, 200 ans après!


  Source : Théorie Analytique, BnF
 Manuscrit, Source : BnF
 Fourier est sûr de pouvoir traiter n'importe quel cas qu'on lui proposera. Il se pose donc en arbitre de la Contoverse des Cordes Vibrantes, et, déférence gardée envers Euler, n'hésite plus à lui donner tort en la circonstance. 
"Il résulte de mes recherches sur cet objet que les fonctions arbitraires même discontinues peuvent toujours être représentées par les développements en sinus ou cosinus d'arcs multiples, et que les [soltions de l'équation de la chaleur] qui contiennent ces développements sont précisément aussi générales que celles ou entrent les fonctions arbitraires d'arcs multiples. Conclusion que le célèbre Euler a toujours repoussée. "
Fourier (1805), cité par I. Grattan-Guinness



 (Source :Planches de la Théorie Analytique, BnF)


 Et la Convergence, dans tout ça?

 Pas de démonstration de convergence dans la Théorie Analytique, mais des affirmations appuyées.  Pourtant, autant la première montre un Fourier maîtrisant parfaitement la notion de convergence, et, plus, la notion moderne de vitesse de convergence, autant la seconde pourrait être taxée de légéreté: il referme une boîte de Pandore au contenu diabolique!

"En général, les séries auxquelles nous sommes parvenus, en développant les diverses fonctions, sont toujours convergentes; mais il ne nous a point paru nécessaire de le démontrer ici: car les termes qui composent ces suites ne sont que les coefficients  des termes qui donnent les valeurs des températures; et ces coefficients affectent des quantités exponentielles, qui décroisseent très rapidement, en sorte que ces dernières séries sont très convergentes. "
Fourier, Théorie Analytique de la Chaleur, ch III, § 228 ( 1822)

 Eh oui... la Physique a repris le dessus! L'objet du traité, ce ne sont pas les séries trigonométriques, mais la résolution de l'équation de la chaleur. Dans l'esprit de Fourier, les coefficients sont essentiels, non pour la série (notations du premier exemple)

a cos y + b  cos 3y + c cos 5y + d cos 7y +...
mais pour
a e -xcos y + b e -3xcos 3y + c e -5xcos 5y + d e -7xcos 7y+...
et là, grâce aux exponentielles, la série converge, et converge très vite (ce qui est numériquement précieux: en général, 3 termes suffiront, a-t-il dit plus haut...). L'évaluation numérique de quelques premiers coefficients permettra la confrontation théorie/expérience sur la température dans la lame; dès lors, pourquoi s'inquiéter du développement au bord? La température au bord est une donnée; une fois qu'on a pu en tirer les coefficients, il n'y a plus de raisons d'y revenir...

On pourrait croire l'auteur pris par un remords: c'est bien vers la première série qu'il revient, mais pour affirmer sans l'ombre d'une justification:

"À l'égard de celles où il n'entre que des sinus ou des cosinus d'arcs multiples, il est également facile de prouver qu'elles sont convergentes, quoiqu'elles représentent les ordonnées des lignes discontinues. [...] Or on démontre rigoureusement que les suites dont il s'agit satisfont à cette dernière condition  [Fourier a repris, juste avant, la définition rigoureuse d'une série convergente, donnée au §177, que nous avons notée D en marge] . "
Fourier, Théorie Analytique de la Chaleur, ch III, § 164 ( 1822)

Sans doute, les nombreux exemples détaillés dans le chapitre III vont tous dans le même sens. Notamment, les fonctions continues qu'il a considérées, parce qu'elles sont plus que continues (les arcs ont en tout point une tangente, ou des demi-tangentes à droite et à gauche) lui ont donné des cas dont la convergence absolue est flagrante.
A-t-il généralisé trop hâtivement? Parce que son objet d'étude l'amène ailleurs, il passe à côté d'un champ qui va prendre plus de 150 ans à explorer...

Quelle Suite dans la Théorie Analytique de la Chaleur de Fourier?


C'est un crescendo dans la difficulté et les symétries du domaine que va entamer Fourier.
Le premier cas, pour lequel on voit ci-contre le croquis manuscrit de l'auteur, sera celui d'un anneau circulaire; puis viendront la sphère, le cylindre...


et là, nous vous disons:

Manuscrit, Source : BnF

Quelle Suite dans l'Étude des Séries de Fourier?

Le "petit historique succint" que le Mathouriste vous promettait depuis mongtemps a pris... un peu trop d'ampleur pour être ici, sous peine d'allonger exagérément cette page. Car même racontée succintement, c'est une longue histoire....
Vous la retrouverez donc en suivant ce lien.

Références


Jean-Pierre Kahane: une vie au service de l'Analyse de Fourier! (Mai 2011, École Polytechnique )
On reconnait au tableau l'évocation de la naissance de la toute première série écrite par Fourier
 dans le Mémoire déposé à l'automne 1811 à l'Académie des Sciences, qui obtiendra le Grand Prix 1812.

 Dire qu'il y a des centaines d'ouvrages consacrés à l'Analyse de Fourier n'est sans doute en rien exagéré. Le Mathouriste se limitera, au moins pour l'instant, au choix amoureux de quelques ouvrages qui l'ont particulièrement séduit, et qu'il a classés par ordre d'accessibilité mathématique :
  •  B. BURKE-HUBBARD, Ondes et Ondelettes (Belin-Pour la Science)
  • G. TOLSTOV, Fourier Series (Dover)
  • H.POINCARÉ,Théorie Analytique de la Propagation de la Chaleur  (G. Carré, 1895 -disponible en ligne sur Gallica-BnF)
  • H. LEBESGUE, Leçons sur les Séries Trigonométriques (Gauthier-Villars 1906 -disponible en ligne sur Gallica-BnF)
  • C. GASQUET, P.WITOMSKI, Analyse de Fourier et Applications (Dunod)
  • E. PRESTINI, The Evolution of Applied Harmonic Analysis: Models of the Real World (Birkhaüser)
  • T. KÖRNER, Fourier Analysis (Cambridge University Press)
  • J.-P. KAHANE, P.-G. LEMARIÉ, Séries de Fourier et Ondelettes (Cassini)
On trouvera aussi sur le site BibNum:

  •  Une analyse  du chap. III, sections I & II, p. 159-177. de la Théorie analytique de la chaleur (1822)

  •  dans la page consacrée au problème de Sturm-Liouville, une présentation élémentaire de la méthode de Fourier, celle qu'il inaugure avec succès dans la Théorie Analytique: on y étudie trois exemples issus du Mémoire, en progressant du cas le plus simple au plus élaboré, respectant ainsi le modèle de démarche de son ouvrage. Le développement d'une fonction en série de fonctions orthogonales est en effet une généralisation de celui de Fourier -incontournable dans la Physique contemporaine, et l'une des preuves de l'extraordinaire fécondité de son travail.

Oeuvres de Fourier disponibles en téléchargement sur le site de la B.N.F.

 Et aussi...


Aller à la Page: l'Armille, la Sphère, le Cylindre et les Autres...  (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformée de Fourier             (Promenade dans la Théorie Analytique, #3)

Aller à la Page: Naissance de la FFT: Fast and Fourier !           (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page:  Signaux, Transformées... et Applications          (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page:  Cristallographie, Optique, Spectroscopie...        (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page:  Spectroscopie par FFT en exploration spatiale    (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page:  Brève Histoire des Séries Trigonométriques   (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page:  De Gabor aux Ondelettes                                    (Promenade dans... la suite de l'histoire, #5)
Aller à la Page:  De Pythagore à Parseval                                      (Promenade dans... la suite de l'histoire, #6)

 Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom?      (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes  (Prélude à la Théorie Analytique, #0.2)

Aller à la Page:  du Refroidissement  de la Terre à l'Effet de Serre  (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées          (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes   (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire          (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres                                       (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane                                                                 (une vie pour Fourier...)


Revenir à la Page Biographique


Revenir à la Home Page du Mathouriste