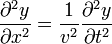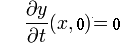Harmonique, vous avez dit: Analyse Harmonique?
... Une Promenade Fouriériste! (Partie 0.1)
Cette page est un préliminaire
à notre promenade dans la Théorie
Analytique de
la Chaleur. Sa lecture n'est pas indispensable
pour lire les suivantes, mais elle peut (en tout cas, l'auteur
l'espère) aider à mieux appréhender le
travail de
Fourier:
Nous savons faire aujourd'hui ce travail, et, magnifique retour sur investissement de la théorie de Fourier, les instruments de laboratoire qui démontent le signal acoustique pour nous révéler ses secrets ont pour fondement mathématique la transformation de Fourier (voir La Partie 3 de notre promenade), et pour implémentation informatique l'algorithme de transformation rapide (voir également La Partie 3). Voici, pour vous allécher, un exemple, que nous expliquerons mathématiquement plus loin: si, dans le saxophone, toutes les harmoniques (toutes les multiples de la fréquence de la note émise, ici un La 880Hz) sont présentes, pour la clarinette en revanche, les multiples pairs sont absents, ou négligeables! Deux tuyaux sensiblement de même longueur (si on considère le sax soprano) , le même type de bec et d'anche... à vous d'observer la (les?) différence(s), et rendez-vous en bas de page...
Ainsi donc, les problèmes de l'harmonie musicale se dessinent-ils, peu à peu, à partir des harmonies naturelles d'une corde en vibration: celles qui correspondent aux sinusoïdes des séries de Fourier. Mais, hélas, elles posent de nombreux problèmes: outre les précédents, elles rendent impossible la transposition (jouer le même air, un ton, ou une tierce au dessus, par exemple), tout simplement parce que les rapports de notes ne seraient pas conservés. Pas étonnant que Marin Mersenne étudie longuement ces questions dans son Harmonie Universelle...

Il est là, discutant avec Desargues, mais un peu caché par Pascal, le père Mersenne!
Grand escalier de la Sorbonne (Paris)
Il dépense beaucoup d'énergie pour faire le point sur ces rapports (au lieu de fréquences, il parle de battements de l'air, mais cela revient au même!)
Son travail encyclopédique a le mérite de dresser l'état des lieux à l'époque de la parution (1636), intégrant les éléments les plus récents, l'Harmonices Mundi de Kepler (1619) et ses correspondances hasardeuses entre orbites des planètes et intervalles musicaux, mais surtout les idées laissées à l'état de manuscrit par Simon Stevin (1605) sur la construction de la gamme tempérée, divisant l'octave en douze intervalles égaux -ce qui revient à prendre pour demi-ton la racine douzième de 2. Ainsi, plus aucun harmonique n'est naturel , pas même la quinte: le rapport naturel 3/2 = 1,5 se voit substituer 2 7/12 = 1,49830... (elle comporte 7 demi-tons) mais il est possible d'écrire dans toutes les tonalités, et une magistrale mise en travaux dirigés, "pour la pratique et le profit des jeunes musiciens désireux de s'instruire et pour la jouissance de ceux qui sont déjà rompus à cet art" fut proposée en deux temps (1722,1744). Conseil partial du Mathouriste: laissez Glenn Gould aux snobs, et faites votre délice de la version de Keith Jarrett ( commencez donc là : prélude 1 du livre 1et poursuivez). Ah, oui: on allait presque oublier de mentionner son auteur, mais vous l'aviez sans doute deviné...
Le sujet "Gammes et Mathématiques" est extraordinairement riche, passionnant -malheureusement trop mal connu des enseignants de théorie musicale, souvent peu ou pas préparés à répondre aux questions intelligentes d'un apprenti musicien un peu curieux. Mais il nous éloignerait trop de Fourier, ce qui nous a obligé à limiter drastiquement ce paragraphe, qu'il faut conclure ainsi: c'est bien la même notion d'harmonie qui est en jeu, mais la musique a dû s'écarter légèrement des harmonies naturelles pour assurer le tempérament. D'ailleurs, cela ne résoudra pas tout: lorsque des instruments jouent ensemble une même note (a fortiori un accord) , chacun émet aussi ses propres harmoniques naturelles... dont le mélange, pour le coup, échappe au tempérament!
Enfin les vibrations d'une corde... peuvent même, par résonance mécanique (transmise par l'air), engendrer celles d'une corde voisine, pour peu que la fréquence à vide de cette dernière soit une harmonique naturelle de la première. Descartes le remarque dans son Compendium Musicae (1618):
À l'autre extrémité de l'histoire de la musique, les compositeurs contemporains ont exploité les résonances naturelles: ainsi Luciano Berio, dans la Sequenza X pour trompette (1984), où le son de la trompette fait entrer en résonance les cordes d'un piano proche, ou encore Pierre Boulez, dans le Dialogue de l'ombre double, l'excitateur étant cette fois une clarinette (1985). Incidemment, ette œuvre est une dédicace à Luciano Beerio pour son 60ème anniversaire.
Quand on y réfléchit bien, tout est
arrivé
à cause de Lucille, ou tout au moins... d'une de ses
sœurs
un peu plus âgée. Vous ne connaissez pas Lucille?
On vous
la présente!
Le problème se présente donc sous une forme très similaire à celui que rencontrera Fourier dans l'étude de la chaleur; la différence la plus notoire porte sur la dérivée temporelle, du second ordre ici, du premier pour la chaleur. D'Alembert a de la chance: un changement de variable banal, mais physiquement pertinent eu égard à la propagation de l'onde et de l'onde réfléchie
permet d'obtenir la solution de l'équation sous la forme
Le son sec, incisif, plus rock de la Solid Body -la caisse est réduite à une planche pleine- a peu de choses en commun -la note fondamentale, tout de même...- avec celui plus riche, chaud, naturellement jazzy de la Gibson à la profonde caisse de résonance ; or les deux se jouent avec une amplification. Où se cache la différence? Dans la présence ou l'absence d'une caisse de résonance, ce qui modifie le dosage des harmoniques, évidemment: on pourrait le voir sur des spectrogrammes comme ceux de la clarinette et du sax soprano. Plus subtil encore, si vous revenez à B.B. King, vous noterez que sa Gibson est une "demi-caisse", d'épaisseur moitié par rapport à celle qu'emploie Kenny Burrell: on peut parier pour les mêmes harmoniques, en gros, mais avec un dosage légèrement différent.
N'hésitez pas à réaliser vous même, grâce à ce site, vos propres courbes de Lissajous correspondant aux intervalles musicaux évoqués plus haut (les rapports de fréquence vous sont rappelés dans la page pour plus de commodité).
Lissajous n'était toutefois que... le deuxième à découvrir "ses" courbes; un dispositif purement mécanique avait été inventé en 1815 par un "sorcier de Salem", l'américain Bowditch (1773-1838), encore afin de comparer deux fréquences, mais celles de deux pendules. Significativement, son appareil fut dénommé harmonographe!
Helmholtz écrit en 1863 une Théorie Physiologique de la Musique, traduite en Français dès 1868. L'ouvrage est remarquablement pédagogique, s'efforçant de présenter les questions abordées sous une forme lisible par tous, tout en ne concédant rien à la rigueur scientifique, cherchant à expliquer et non asséner ex cathedra: bref, l'anti Théorie de la Musique à la sauce Danhauser (conçue en 1872); les explications mathéatiques se trouvent repoussées dans des suppléments en fin d'ouvrage, dont le lecteur peut disposer à sa guise suivant son niveau d'études. Savourons, à titre d'exemple, sa présentation de la sinusoïde, courbe de base pour comprendre toute la physique vibratoire:
Il paie tribut à Lissajous quand il étudie les cordes frottées (ex: le violon), créant ce qu'il nomme "microscope à vibrations" grâce auquel il observe un petit grain placé sur la corde: une coordonée est donnée par la vibration d'un diaposon portant une loupe, l'autre par celle de la corde.
Et c'est plus loin Fourier à qui il rend hommage!
Voilà de quoi être en...harmonie avec le vibrant
plaidoyer par lequel Fourier introduit son ouvrage:
Aujourd'hui, synthétiser se fait avec un... synthétiseur. Mais avant?
D'abord, l'instrument acoustique poussant le plus loin le principe de synthèse harmonique est l'orgue. Il suscite l'intérêt théorique de ... Mersenne et Bernoulli, comme par hasard. Et, ô surprise, voyez qui, en 1865, est responsable du rapport sur la rénovation de l'orgue de Saint Sulpice, à Paris!
Néanmoins, s'il réalise, par sa mécanique de tirettes, l'utilisation simultanée de plusieurs tuyaux, il faut bien remarquer qu'il s'agit d'une synthèse de sons dont chacun est déjà composé: aucun tuyau n'émet un son pur, sinusoïdal.
Or, un synthétiseur de sons sinusoïdaux a bel et bien existé, avant l'époque des circuits intégrés, dès le temps héroïque des amplis à lampes: c'est l'orgue Hammond, conçu en 1934, dont le modèle phare B3, a fait les belles heures des églises baptistes et des petits combos jazz des années 1950-60. Avec son pivot central "The Incredible" Jimmy Smith: tendez une petite oreille (et un petit oeil) à Organ Grinder's Swing avec Kenny Burrell à la guitare, pour vous remettre en mémoire les cordes vibrantes à la Gibson, ou le non moins emblématique Midnight Special. Avant, il y a Milt Buckner et Wild Bill Davis, après, en digne fils spirituel, le jeune et bouillant Joey de Francesco (un excellent concert en compagnie de David Sanborn au sax alto)...
L'idée géniale est de construire tous les sons à partir d'une sinusoïde pure par excellence: celle du courant secteur (60Hz aux USA). Au dessus de chaque touche, des tirettes (bien visibles sur le Midnight Special recommandé, et encore mieux avec Joey de Francesco -le clavier est souvent filmé en gros plan) permettent d'ajouter à chaque son des harmoniques choisies, chacune avec 8 possibiltés de niveau différentes! C'est donc la mise en œuvre exacte de la synthèse de Fourier, l'instrument qui est le plus proche de sa théorie! Après quoi, vous n'oserez plus jamais prétendre que Fourier, ça ne swingue pas...
Mais disposons nous d'un critère objectif et scientifique pour distinguer les deux? Déjà, Helmholtz tente de répondre, toutefois assez lucide pour affirmer le caractère flou et subjectif de la frontière:
Et à une extrême, justement, il y a le bruit blanc, souvent utilisé par les acousticiens pour faire des mesures pratiques, qu'il s'agisse de qualité des salles de concert ou d'isolation phonique des logements. Il s'agit d'une émission sonore où toutes les fréquences sont présentes, (presque) au même niveau. Le ressenti à l'oreille est un bruit totalement neutre (alors que le bruit de la mer, ou celui d'une salle de concert pendant que le public s'installe, fournissent à l'oreille assez d'éléments pour les distinguer, et les identifier: il y a mélange, excès de fréquences entendues, certes, mais les inégalités de leurs amplitudes permettent de les typer).
Pourquoi blanc, au fait? Par analogie avec la décomposition de la lumière blanche, réussie par Newton à l'aide d'un prisme: tout le spectre des longueurs d'onde audible est présent dans l'un comme tout le spectre des radiations visibles dans l'autre! C'est d'ailleurs Newton qui emploie le premier ce mot dans une lettre à Oldenburg (19/02/1672) et l'officialise dans son Optique (1704)
Sur la vie du mot spectre en physique, puis en mathématiques, on pourra consulter cet article de J. Mawhin; autre agréable introduction (où l'on reparle de cordes vibrantes...), celui de San Vu Ngoc sur le site Images des Mathématiques (CNRS). Si, en mathématiques, le spectre désigne aujourd'hui l'ensemble des valeurs propres, il le doit justement aux modes propres de vibration!
- en précisant certains éléments historiques qui entourent cette découverte;
- en se plaçant dans un contexte a priori plus naturel et plus accessible parce que plus familier: celui des ondes sonores et des instruments de musique;
- la musique adoucit les mœurs... et peut être aussi les équations! (Promis, il n'y en aura pas trop)... et le Mathouriste se souvient qu'il fut aussi un Jazztouriste!
"Mais
pourquoi l'Analyse de Fourier n'est-elle pas
née de l'étude de la musique et des hauteurs
sonores? "
De fait, tous les ingrédients étaient
là... tous, sauf Fourier!
"Un seul être vous manque, et tout est
dépeuplé..."Mise en Bouche (Contemporaine)
Le son d'un instrument de musique est une vibration de l'air, elle-même engendrée une vibration d'origine mécanique, par exemple une corde (violon, guitare, piano), une lame de bois (clarinette) ou de métal (harmonica, accordéon). Un diapason émet un son "pur" qui, on le verra un peu plus loin, correspond à une sinusoïde dont la fréquence est de 440 Hertz (ou battements par secondes). Mais personne ne confondrait le La 440 d'une clarinette avec celui d'une trompette: c'est qu'il y a donc autre chose dans le son émis que cette fréquence, dénommée fondamentale. Ce qui donne à chaque instrument son timbre particulier, ce qui "colore" sa fondamentale, ce sont d'autres vibrations produites simultanément par l'instrument; elles dépendent de sa forme, de sa matière, mais ont des fréquences multiples de celle de la fondamentale: ce sont elles qu'on nomme les harmoniques. Et comme une couleur s'obtient en sélectionnant d'abord les couleurs de base qui la composeront, puis en dosant les quantités, un timbre peut se construire en choisissant les harmoniques qui l'accompagneront, puis en les dosant. Ou comme une pâtisserie s'obtient en choisissant les produits de base (farine, sucre, chocolat...) puis en dosant leur proportions respectives. Mais il y a une énome différence: si depuis toujours le peintre à partir des pigments, le cuisinier à partir des ingrédients, le parfumeur à partir des fragrances, ont synthétisé le résultat à déguster avec nos sens, il a fallu attendre le XXème siècle et l'électronique pour être capable de faire de même dans le domaine sonore. Dès l'antiquité, les physiciens ont été confronté à un problème qu'on qualifierait aujourd'hui de reverse engineering: faire l'analyse du son pour en trouver les ingrédients et le dosage.Nous savons faire aujourd'hui ce travail, et, magnifique retour sur investissement de la théorie de Fourier, les instruments de laboratoire qui démontent le signal acoustique pour nous révéler ses secrets ont pour fondement mathématique la transformation de Fourier (voir La Partie 3 de notre promenade), et pour implémentation informatique l'algorithme de transformation rapide (voir également La Partie 3). Voici, pour vous allécher, un exemple, que nous expliquerons mathématiquement plus loin: si, dans le saxophone, toutes les harmoniques (toutes les multiples de la fréquence de la note émise, ici un La 880Hz) sont présentes, pour la clarinette en revanche, les multiples pairs sont absents, ou négligeables! Deux tuyaux sensiblement de même longueur (si on considère le sax soprano) , le même type de bec et d'anche... à vous d'observer la (les?) différence(s), et rendez-vous en bas de page...
| Instruments et solistes | Signal sonore (fonction du temps) | Fréquences présentes |
| |
à Nice-Cimiez:
Brandford Marsalis (ss, 8/7/1990, 22h) et Eddie Daniels (cl, 19/7/1992)
Images des signaux et des fréquences issues du site Physics of Music
Images des signaux et des fréquences issues du site Physics of Music
Et
maintenant, apprécions la différence à
l'oreille,
et cela peut se faire sur autre chose que de mornes sons
filés.
Rien ne vaut de goûter le saxophone
soprano avec celui qui l'a inventé: Sidney Bechet,
qu'accompagnait depuis son arrivée en France... Claude
Luter,
encore à la clarinette! Idéal pour confronter les
deux
instruments.
Pour un répertoire plus authentiquement Néo-Orléanais, voir ce Saint Louis Blues: le son est de très piètre qualité (l'image aussi, mais le document garde un intérêt!), et pourtant, impossible de confondre les deux, qui prennent chacun leur solo.
Pour un répertoire plus authentiquement Néo-Orléanais, voir ce Saint Louis Blues: le son est de très piètre qualité (l'image aussi, mais le document garde un intérêt!), et pourtant, impossible de confondre les deux, qui prennent chacun leur solo.
Trouver l'Harmonie: Plus Compliqué qu'on ne Croirait...
Comment est-on arrivé là? L'histoire remonte -au moins!- à Pythagore. On a fait une légende de sa découverte dans l'échoppe d'un forgeron: les marteaux de Pythagore, comme il y a la baignoire d'Archimède et la pomme de Newton. Mais dans toute légende scientifique, il y a un fond de vérité, de sens de l'observation, et de curiosité essentielle pour pousser l'investigation en profondeur. Alors, tant qu'à se servir une légende romancée... n'ayons pas peur de la lire dans un roman!|
le livre de Zarlino, 1558 (Université de Strasbourg) |
À la renaissance,
Gioseffo Zarlino ( 1517-)
a tenté d'améliorer les choses, utilisant la
cinquième harmonique pour engendrer la tierce majeure (et la
tierce mineure suivra grâce au rapport inverse, 5/6).
Mais que faire de la septième harmonique? D'autre part, ce système fait que le ton du do au ré (9/8) ne vaut pas exactement le même rapport que le ton du ré au mi (10/9)... |
Ainsi donc, les problèmes de l'harmonie musicale se dessinent-ils, peu à peu, à partir des harmonies naturelles d'une corde en vibration: celles qui correspondent aux sinusoïdes des séries de Fourier. Mais, hélas, elles posent de nombreux problèmes: outre les précédents, elles rendent impossible la transposition (jouer le même air, un ton, ou une tierce au dessus, par exemple), tout simplement parce que les rapports de notes ne seraient pas conservés. Pas étonnant que Marin Mersenne étudie longuement ces questions dans son Harmonie Universelle...
Il est là, discutant avec Desargues, mais un peu caché par Pascal, le père Mersenne!
Grand escalier de la Sorbonne (Paris)
Il dépense beaucoup d'énergie pour faire le point sur ces rapports (au lieu de fréquences, il parle de battements de l'air, mais cela revient au même!)
Son travail encyclopédique a le mérite de dresser l'état des lieux à l'époque de la parution (1636), intégrant les éléments les plus récents, l'Harmonices Mundi de Kepler (1619) et ses correspondances hasardeuses entre orbites des planètes et intervalles musicaux, mais surtout les idées laissées à l'état de manuscrit par Simon Stevin (1605) sur la construction de la gamme tempérée, divisant l'octave en douze intervalles égaux -ce qui revient à prendre pour demi-ton la racine douzième de 2. Ainsi, plus aucun harmonique n'est naturel , pas même la quinte: le rapport naturel 3/2 = 1,5 se voit substituer 2 7/12 = 1,49830... (elle comporte 7 demi-tons) mais il est possible d'écrire dans toutes les tonalités, et une magistrale mise en travaux dirigés, "pour la pratique et le profit des jeunes musiciens désireux de s'instruire et pour la jouissance de ceux qui sont déjà rompus à cet art" fut proposée en deux temps (1722,1744). Conseil partial du Mathouriste: laissez Glenn Gould aux snobs, et faites votre délice de la version de Keith Jarrett ( commencez donc là : prélude 1 du livre 1et poursuivez). Ah, oui: on allait presque oublier de mentionner son auteur, mais vous l'aviez sans doute deviné...
| Thomaskirche (Leipzig,
Allemagne) : devant, et à l'intérieur. Noter
que l'orgue, son instrument chéri, obeit au même
principe
physico-acoustique que les cordes: un tuyau ouvert, par
exemple,
sonne d'autant plus est grave qu'il est plus long.
|
||
Le sujet "Gammes et Mathématiques" est extraordinairement riche, passionnant -malheureusement trop mal connu des enseignants de théorie musicale, souvent peu ou pas préparés à répondre aux questions intelligentes d'un apprenti musicien un peu curieux. Mais il nous éloignerait trop de Fourier, ce qui nous a obligé à limiter drastiquement ce paragraphe, qu'il faut conclure ainsi: c'est bien la même notion d'harmonie qui est en jeu, mais la musique a dû s'écarter légèrement des harmonies naturelles pour assurer le tempérament. D'ailleurs, cela ne résoudra pas tout: lorsque des instruments jouent ensemble une même note (a fortiori un accord) , chacun émet aussi ses propres harmoniques naturelles... dont le mélange, pour le coup, échappe au tempérament!
Enfin les vibrations d'une corde... peuvent même, par résonance mécanique (transmise par l'air), engendrer celles d'une corde voisine, pour peu que la fréquence à vide de cette dernière soit une harmonique naturelle de la première. Descartes le remarque dans son Compendium Musicae (1618):
«
Dans les cordes de luth, si on en pince une, celles qui sont plus
élevées qu’elle d’une octave ou d’une
quinte tremblent et résonnent d’elle même »
Il arrive que l'on exploite sciemment ce
phénomène: dans la facture instrumentale d'abord, comme
dans les violes d'amour: ce sont des violes, dotées au XVIIème siècle de cordes sympathiques,
excitées sans être touchées, par la seule vibration
d'une corde frottée voisine si leurs
fréquences propres sont en sympathie, on dirait aujourd'hui: en harmonie! | violes d'amour, au musée de la Cité de la Musique (Paris) Les
cordes sympathiques sont bien visibles (en agrandissant l'image!)
à l'arrière plan des cordes que frotte l'archet. Il est
clairement impossible pour celui-ci de les atteindre, seule la
résonance peut les mettre en mouvement.
|
|
À l'autre extrémité de l'histoire de la musique, les compositeurs contemporains ont exploité les résonances naturelles: ainsi Luciano Berio, dans la Sequenza X pour trompette (1984), où le son de la trompette fait entrer en résonance les cordes d'un piano proche, ou encore Pierre Boulez, dans le Dialogue de l'ombre double, l'excitateur étant cette fois une clarinette (1985). Incidemment, ette œuvre est une dédicace à Luciano Beerio pour son 60ème anniversaire.
L'Affaire des Cordes Vibrantes
| la mythique Lucille, au B.B. King Museum d'Indianola ( Mississippi, USA) | |
à moins qu'on
ne laisse ce soin à celui dont elle a partagé la
vie...
Prenez le temps d'écouter le dialogue du bluesman et de sa guitare, d'apprendre du boss lui-même l'origine de son nom... et pourquoi pas vous offrir un petit concert en vidéo, Live at Nick's à Dallas (Texas), par exemple (histoire de vérifier que l'annonce ci-dessus n'a rien d'exagéré!) et si, après ça, vous n'avez pas envie de savoir ce qui se passe quand la corde de guitare est mise en vibration, le Mathouriste ne peut plus rien pour vous! (Ou alors, écrivez lui, et il vous conseillera quelques autres concerts du même, ou quelques autres guitar-heroes de sa discothèque...)
La première mise en évidence expérimentale des harmoniques fut l'œuvre... d'un théoricien, Joseph Sauveur (1653-1716), mathématicien de son état, considéré comme fondateur de l'acoustique.
Il vient de mettre en évidence ce que l'on appelera bientôt modes propres de vibrations de la corde: propres, parce qu'ils lui appartiennent en propre! La fixation aux deux bouts donne un statut privilégié aux vibrations correspondant aux divisions entières de la longueur; ce ne sont donc pas toutes les fréquences, mais une famille privilégiée, celle des harmoniques de la fondamentale.
Signalons aux apprentis mathématiciens que c'est de là que naîtront les dénominations valeurs propres, fonctions propres, et enfin vecteurs propres... quand on commencera à regarder les fonctions comme des vecteurs, deux bons siècles plus tard!
"Ladies
and Gentlemen, Mister Be... BEEEE... KING
!!!!!!!"
Prenez le temps d'écouter le dialogue du bluesman et de sa guitare, d'apprendre du boss lui-même l'origine de son nom... et pourquoi pas vous offrir un petit concert en vidéo, Live at Nick's à Dallas (Texas), par exemple (histoire de vérifier que l'annonce ci-dessus n'a rien d'exagéré!) et si, après ça, vous n'avez pas envie de savoir ce qui se passe quand la corde de guitare est mise en vibration, le Mathouriste ne peut plus rien pour vous! (Ou alors, écrivez lui, et il vous conseillera quelques autres concerts du même, ou quelques autres guitar-heroes de sa discothèque...)
La première mise en évidence expérimentale des harmoniques fut l'œuvre... d'un théoricien, Joseph Sauveur (1653-1716), mathématicien de son état, considéré comme fondateur de l'acoustique.
|
|
||
| Le Système
général
de Sauveur in Mémoires de l'Académie
Royale des sciences (1701) . Noter la parfaite définition de l'harmonique, avec l'exemple le plus simple hors l'octave: le triplement de la fréquence; celle des nœuds et ventres, toujours en usage. La figure, elle, concerne le quintuplement de la fréquence, en immobilisant la corede à 1/5 ou 2/5 de sa longueur pour y créer un nœud. |
||
Il vient de mettre en évidence ce que l'on appelera bientôt modes propres de vibrations de la corde: propres, parce qu'ils lui appartiennent en propre! La fixation aux deux bouts donne un statut privilégié aux vibrations correspondant aux divisions entières de la longueur; ce ne sont donc pas toutes les fréquences, mais une famille privilégiée, celle des harmoniques de la fondamentale.
Signalons aux apprentis mathématiciens que c'est de là que naîtront les dénominations valeurs propres, fonctions propres, et enfin vecteurs propres... quand on commencera à regarder les fonctions comme des vecteurs, deux bons siècles plus tard!
Solutions et Premières Escarmouches
Brook Taylor, le premier, avait utilisé le calcul différentiel (à une seule variable) pour montrer qu'une sinusoïde (sin ax).(cos avt) peut représenter une vibration d'une corde tendue, fixée aux deux bouts (1715). Mais la première véritable mise en équation complète est due à d'Alembert (1747); c'est aussi la première fois qu'on forme une équation aux dérivées partielles. Le cadre pertinent est celui de petites oscillations transversales (perpendiculairement à la corde au repos): l'ordonnée d'un point est fonction de son abcisse sur la corde, et du temps. Cette équation s'accompagne de conditions aux limites évidentes: il est bon que la corde reste fixée aux deux extrémités, et d'une condition intiale, qui, dans le cas de la corde pincée, représente la déformation initiale de la corde avant qu'elle ne soit lâchée. L désigne la longueur de la corde, v la célérité de propagation de l'onde dans le milieu. |
|
Le problème se présente donc sous une forme très similaire à celui que rencontrera Fourier dans l'étude de la chaleur; la différence la plus notoire porte sur la dérivée temporelle, du second ordre ici, du premier pour la chaleur. D'Alembert a de la chance: un changement de variable banal, mais physiquement pertinent eu égard à la propagation de l'onde et de l'onde réfléchie
u = x - vt ; w = x + vt
y (x, t) = F(x + vt) + G(x - vt)
et
après exploitation de la condition en x = 0
y (x, t) = F(x + vt) - F(vt - x)
où F est une fonction arbitraire,
à qui la condition initiale de vitesse imposera
d'être impaire et la condition en x = 0
d'être 2L-périodique.
Arbitraire... oui, mais pas tant que cela; d'Alembert la voulait définie "par une seule formule" (autrement dit, il n'admettait pas une définition par morceaux), et deux fois continûment dérivable ("sans sauts de courbure"), pour pouvoir la reporter dans l'équation et effectuer les dérivations requises. Ce deuxième point se tenait, mathématiquement, mais Euler, qui avait résolu l'équation à peu près en même temps argumenta avec bon sens à partir du problème physique:
Décidément, Lucille a le chic pour déclencher les bagarres. Celle-ci va opposer un nouveau venu, Daniel Bernoulli, à Euler et d'Alembert. Sa méthode est radicalement différente (1755): sans étudier l'équation, il somme les solutions sinusoïdales de Taylor (en série, c'est à dire: une infinité),et propose une expression de la solution qui ne peut qu'être confrontée à celle de d'Alembert: est-ce-ce la même?
Il est bon de signaler qu'à cette époque, le "principe de superposition" ne va pas de soi, tant que le problème n'a pas clairement été formulé comme une équation linéaire. Quant à sommer un nombre fini ou infini de termes, aucune différence: c'est toujours sommer! Et, surprise, Euler a effectivement écrit la même série dans l'article E140 de 1748, mais comme un exemple possible, presque sans y attacher d'importance.
Euler ne peut que réagir; il commence par exprimer un doute plutôt étonnant de sa part: une série de solutions est-elle encore solution? ("le nombre infini semble détruire la nature...."). Après avoir concédé que cela peut fonctionner, sur un exemple où il sait calculer effectivement la somme il va poser le problème avec clarté et pertinence: toute forme de courbe est-elle représentable par une telle série?
Sincérité ou roublardise -pour mieux faire triompher son point de vue?- Euler se lance dans une sorte de débat entre les deux positions en présence. Physique et mathématiques y dialoguent aussi: sur le versant physicien, il rappelle le caractère absolument arbitraire de la forme initiale de la corde (pp. 200,201); mathématiquement, alors même qu'il n'est pas prêt à franchir le pas d'une définition de fonction correspondante et qui deviendra la définition moderne, il doute clairement de la possibilité d'une représentation de toute fonction comme somme d'une telle série (p. 200): la combinaison des trochoïdes "ne saurait être que très particulière", mais pour tout argument, il martèle "il est bien clair que" comme le premier étudiant venu qui ne sait comment se sortir (autrement, de préférence un peu plus dignement) d'une démonstration. Euler n'est pourtant pas le premier venu... il y a de quoi consoler les étudiants (mais oui, même les grands, même les meilleurs font aussi de mauvais raisonnements!)
D'Alembert est, sur ce point, dans le même camp qu'Euler; on comprend dès lors le sentiment de triomphe de Fourier parvenant à une conclusion, certes exagérément optimiste mathématiquement, mais valable pour tout signal physique (en particulier sonore):
Daniel Bernoulli n'a pas poussé plus loin son avantage, et voilà comment trois éminents savants passent à côté des séries trigonométriques pour le problème qui les appelle de la façon la plus naturelle. Fourier ne manquera pas de le faire observer pour souligner l'importance de son apport personnel face à un jury qui a totalement sous-estimé les avancées que contient son travail dès 1807
Arbitraire... oui, mais pas tant que cela; d'Alembert la voulait définie "par une seule formule" (autrement dit, il n'admettait pas une définition par morceaux), et deux fois continûment dérivable ("sans sauts de courbure"), pour pouvoir la reporter dans l'équation et effectuer les dérivations requises. Ce deuxième point se tenait, mathématiquement, mais Euler, qui avait résolu l'équation à peu près en même temps argumenta avec bon sens à partir du problème physique:
| "La
première vibration dépend de notre bon plaisir,
puisqu'on peut, avant de
lâcher la corde, lui donner une figure quelconque." [...] "Ayant donc décrit
une semblable courbe anguiforme,
soit régulière, contenue dans une certaine
équation, soit
irrégulière, ou méchanique,
son appliquée quelconque PM fournira les fonctions, dont
nous avons besoin pour la solution du Problême."
|
||
| exemple de coube "anguiforme" (faisant un angle): c'est le cas le plus naturel quand on pince la corde d'une guitare avant de la lâcher! | ||
La Controverse des Cordes Vibrantes
L'expression est devenue célèbre; elle provient des termes mêmes employés par d'Alembert| "J'ai
parlé de vous dans ma Préface, comme je le dois
à
tous égards, à l'occasion de notre controverse sur la
vibration des cordes." d'Alembert
à Lagrange, Lettre, 29 avril 1768
|
Décidément, Lucille a le chic pour déclencher les bagarres. Celle-ci va opposer un nouveau venu, Daniel Bernoulli, à Euler et d'Alembert. Sa méthode est radicalement différente (1755): sans étudier l'équation, il somme les solutions sinusoïdales de Taylor (en série, c'est à dire: une infinité),et propose une expression de la solution qui ne peut qu'être confrontée à celle de d'Alembert: est-ce-ce la même?
 |
 |
 |
|
| article complet disponible ici | et sans calculs
épineux (SIC!) |
figures correspondantes à droite | Bernoulli somme, sur la fig.6, les deux harmoniques des fig.1 et fig.2 |
Il est bon de signaler qu'à cette époque, le "principe de superposition" ne va pas de soi, tant que le problème n'a pas clairement été formulé comme une équation linéaire. Quant à sommer un nombre fini ou infini de termes, aucune différence: c'est toujours sommer! Et, surprise, Euler a effectivement écrit la même série dans l'article E140 de 1748, mais comme un exemple possible, presque sans y attacher d'importance.
Bernoulli, et cela
mérite d'être souligné, tient à faire le lien
avec
les harmoniques musicales: si le son
fondamental est un do, de fréquence f1
(par "vibrations Tayloriennes" , il faut naturellement entendre "sinusoïdales", terme alors inusité) |
 |
Euler ne peut que réagir; il commence par exprimer un doute plutôt étonnant de sa part: une série de solutions est-elle encore solution? ("le nombre infini semble détruire la nature...."). Après avoir concédé que cela peut fonctionner, sur un exemple où il sait calculer effectivement la somme il va poser le problème avec clarté et pertinence: toute forme de courbe est-elle représentable par une telle série?
 |
 |
 |
| les 3 premières pages du mémoire E213, disponible en ligne | ||
Sincérité ou roublardise -pour mieux faire triompher son point de vue?- Euler se lance dans une sorte de débat entre les deux positions en présence. Physique et mathématiques y dialoguent aussi: sur le versant physicien, il rappelle le caractère absolument arbitraire de la forme initiale de la corde (pp. 200,201); mathématiquement, alors même qu'il n'est pas prêt à franchir le pas d'une définition de fonction correspondante et qui deviendra la définition moderne, il doute clairement de la possibilité d'une représentation de toute fonction comme somme d'une telle série (p. 200): la combinaison des trochoïdes "ne saurait être que très particulière", mais pour tout argument, il martèle "il est bien clair que" comme le premier étudiant venu qui ne sait comment se sortir (autrement, de préférence un peu plus dignement) d'une démonstration. Euler n'est pourtant pas le premier venu... il y a de quoi consoler les étudiants (mais oui, même les grands, même les meilleurs font aussi de mauvais raisonnements!)
D'Alembert est, sur ce point, dans le même camp qu'Euler; on comprend dès lors le sentiment de triomphe de Fourier parvenant à une conclusion, certes exagérément optimiste mathématiquement, mais valable pour tout signal physique (en particulier sonore):
| "Il
résulte de mes recherches sur cet objet que les fonctions arbitraires même
discontinues peuvent toujours être
représentées par les développements en
sinus ou
cosinus d'arcs multiples, et que les [solutions de
l'équation de
la chaleur] qui contiennent ces développements
sont précisément aussi
générales que celles
ou entrent les fonctions arbitraires d'arcs multiples. Conclusion que
le célèbre Euler a toujours repoussée. " Fourier (1805),
cité par I. Grattan-Guinness
|
Vous saurez au bout de quel long chemin dans notre épisode 1: Naissance des Séries de Fourier .
Daniel Bernoulli n'a pas poussé plus loin son avantage, et voilà comment trois éminents savants passent à côté des séries trigonométriques pour le problème qui les appelle de la façon la plus naturelle. Fourier ne manquera pas de le faire observer pour souligner l'importance de son apport personnel face à un jury qui a totalement sous-estimé les avancées que contient son travail dès 1807
| "À l'égard des
recherches de D'Alembert et d'Euler, ne pourrois-je point ajouter que s'ils ont connu ces
développements, ils n'en ont fait qu'un usage bien imparfait,
car ils étoient persuadés
l'un et l'autre qu'une fonction arbitraire et discontinue ne pourroit
jamais être résolue en séries de ce
genre." Fourier , Lettre à [probablement] Lagrange
|
Traiter l'équation à la Fourier...
Fourier ne l'a pas fait pour ne pas dévier de son étude de la chaleur, mais il aurait pu appliquer facilement sa méthode (dont vous trouverez les détails en page suivante) au problème mis en équation ci-dessus. Les étapes en auraient été:- recherche des solutions à variables séparées u(x,t) = g(x).h(t), ce qui conduit à deux équations différentielles en et (à coefficients constants);
- g(x) = A sin ax + B cos ax doit vérifier les conditions aux limites fixant la corde en x = 0, x = L: B =0 et seuls les an = nπ/L fournissent des solutions non nulles;
- sommer en série, ce qui vérifiera l'équation (en admettant qu'on peut dériver terme à terme);
- la condition initiale de vitesse nulle ne laissera qu'une série Σ Kn (sin anx). (cos ant) ;
- la condition initiale de forme de la corde exigera (en faisant t = 0) que f soit la somme de la série des des Kn (sin anx), ce qui fixera les Kn comme coefficients de Fourier de f
Analyser et Synthétiser le Son
Gibson ou Fender?
Histoire de ne pas quitter trop vite les cordes vibrantes, posons une question de plus (avec nouveau risque de bagarres, chaque camp ayant ses inconditionnels...)Ȇtes-vous
Gibson ou Fender?
|
|
|
| Kenny Burrell et sa Gibson
(à sa gauche, Harold Land) Nice, arènes de Cimiez, 6 Juillet 1984, 21h |
Foley
Mac Creary et sa Fender Solid Body (avec Miles Davis, bien
sûr) Nice, jardins de Cimiez, 17
Juillet 1990, 23h
|
Le son sec, incisif, plus rock de la Solid Body -la caisse est réduite à une planche pleine- a peu de choses en commun -la note fondamentale, tout de même...- avec celui plus riche, chaud, naturellement jazzy de la Gibson à la profonde caisse de résonance ; or les deux se jouent avec une amplification. Où se cache la différence? Dans la présence ou l'absence d'une caisse de résonance, ce qui modifie le dosage des harmoniques, évidemment: on pourrait le voir sur des spectrogrammes comme ceux de la clarinette et du sax soprano. Plus subtil encore, si vous revenez à B.B. King, vous noterez que sa Gibson est une "demi-caisse", d'épaisseur moitié par rapport à celle qu'emploie Kenny Burrell: on peut parier pour les mêmes harmoniques, en gros, mais avec un dosage légèrement différent.
|
|
Si vous
partez Sur la Route de
Memphis,
n'hésitez pas à faire la visite de l'usine
Gibson, c'est
très intéressant! Pour vous aider,
le Mathouriste
a sélectionné une image vous donnant les
horaires... Il
ne peut en faire plus pour vous, car les photos sont strictement
interdites une fois passée la porte. Vous y apprendrez que le secret de sa sonorité unique résiderait dans les 17 couches de vernis que reçoit la guitare. Notez qu'on nous sert souvent la même explication pour la sonorité inégalée des Stradivarius, assortie d'un nombre égal de contestations de cette affirmation. Inutile de dire que ni les unes, ni les autres, n'ont tout avoué aux examens spectroscopiques poussés, nombreux et répétés, qu'ils ont subi! |
|
| Memphis, Tennessee (USA), Night and Day... | ||
Pionniers de l'Analyse Harmonique du Son
|
Au delà de Pythagore,
Mersenne et Sauveur, ce sont des
physiciens de la deuxième mitié du
XIXème
siècle qui réalisent les premiers dispositifs
expérimentaux, avec beaucoup de mérite! Les trois
principaux sont contemporains les uns des autres: Jules Lissajous (1822-1880), Hermann von Helmholtz (1821-1894)
et Alfred Cornu (1841-1902) Lissajous, notamment, conçoit pour la première fois (1857) un dispositif optique permettant de comparer des fréquences (données par des diapasons différents): utilisant ingénieusement des réflexions à angle droit sur de petits miroirs solidaires des fourches, il fait en sorte que deux coordonnées orthogonales x et y soient chacune gouvernées par un des deux diapasons; ainsi l'image ponctuelle de la source lumineuse décrit une courbe paramétrée, à laquelle son nom restera désormais attachée pour les (futurs) électroniciens du monde entier: une courbe de Lissajous. En comparant son travail, ses tableaux de références -noter l'interprétation musicale-à cette page Wikipedia, où l'utilisation en électronique est bien présentée, plus de doute: ce montage'est l'ancêtre mécanico-optique de l'oscilloscope! |
|
| Cornu (au violon) se livrant à la détermination expérimentale des fréquences | |
|
|
|
| Le dispositif expérimental de Lissajous | Courbes de Lissajous en fonction des rapports de fréquences (et des déphasages) |
N'hésitez pas à réaliser vous même, grâce à ce site, vos propres courbes de Lissajous correspondant aux intervalles musicaux évoqués plus haut (les rapports de fréquence vous sont rappelés dans la page pour plus de commodité).
Lissajous n'était toutefois que... le deuxième à découvrir "ses" courbes; un dispositif purement mécanique avait été inventé en 1815 par un "sorcier de Salem", l'américain Bowditch (1773-1838), encore afin de comparer deux fréquences, mais celles de deux pendules. Significativement, son appareil fut dénommé harmonographe!
|
|
||
| Construit vers 1900, mais sur le
modèle original (Science Museum, Londres) |
Exemple
d'images produites (rapport irrationnel ou rationnel peu simple) |
Un modèle plus
récent (1940) et plus précis... plus complexe
aussi! (Science Museum, Londres) |
Helmholtz écrit en 1863 une Théorie Physiologique de la Musique, traduite en Français dès 1868. L'ouvrage est remarquablement pédagogique, s'efforçant de présenter les questions abordées sous une forme lisible par tous, tout en ne concédant rien à la rigueur scientifique, cherchant à expliquer et non asséner ex cathedra: bref, l'anti Théorie de la Musique à la sauce Danhauser (conçue en 1872); les explications mathéatiques se trouvent repoussées dans des suppléments en fin d'ouvrage, dont le lecteur peut disposer à sa guise suivant son niveau d'études. Savourons, à titre d'exemple, sa présentation de la sinusoïde, courbe de base pour comprendre toute la physique vibratoire:
|
"[...]
ce qu'il y a de mieux à faire, c'est de tendre le papier sur
un
cylindre, auquel un mouvement d'horlogerie imprime une
rotation
uniforme. On humecte le papier, et on le fait passer sur une flamme de
térébenthine, de manière à
le couvrir de
noir de fumée; on peut alors facilement y tracer des traits
déliés avec une pointe d'acier fine, un peu
arrondie. La
figure [a] été exécutée
par un diapason, sur le cylindre tournant du phonotaugraphe de MM.
Scott et König. "
Helmholtz, Théorie
Physiologique de la Musique (1863)
|
Il paie tribut à Lissajous quand il étudie les cordes frottées (ex: le violon), créant ce qu'il nomme "microscope à vibrations" grâce auquel il observe un petit grain placé sur la corde: une coordonée est donnée par la vibration d'un diaposon portant une loupe, l'autre par celle de la corde.
|
"On
n'a encore donné aucune théorie
mécanique
complète du mouvement des cordes
ébranlées par
l'archet, parce qu'on ignore la façon dont l'archet agit sur
le
mouvement. Je suis arrivé cependant, dans la limite du
possible,
en m'appuyant sur une méthode particulière dont
le
principe a été trouvé par un physicien
français, M. Lissajous, à observer
la forme de
vibration d'un point isolé de'une corde de violon, et au
moyen
de cette forme qui est relativement très simple,
à
déterminer le mouvement de la corde entière et
l'intensité des harmoniques."
Helmholtz, Théorie
Physiologique de la Musique (1863)
|
|
| Stéphane
Grappelli Nice-Cimiez, 17/07/1987, 23h |
|
|
||
| un modèle de
"Microscope à vibrations" (Musée d'Histoire Naturelle, Lille) |
...le même, dans son
Traité d'Acoustique, avec les fiures engendrées
|
|
Et c'est plus loin Fourier à qui il rend hommage!
|
"La multiplicité des
diverses formes de vibration qu'on peut obtenir ainsi en composant des
vibrations pendulaires n'est pas seulement extraordinairement grande;
elle dépasse toute limite assignable. C'est ce que le
célèbre physicien français Fourier a
prouvé
dans une loi mathématique, que nous pouvons formuler de la
manière suivante, en l'appliquant à notre sujet: toute
forme quelconque de vibration, régulière et
périodique, peut être
considérée comme la
somme de vibrations pendulaires, dont les durées sont une,
deux,
trois, quatre, etc... fois moins grandes que celle du mouvement
donné. [...]
Les amplitudes des vibrations simples composantes [...] peuvent être déterminées, ainsi que l'a montré Fourier, par des méthodes de calcul particulières qui ne comportent pas une exposition élémentaire. Il en résulte qu'un mouvement donné, régulier et périodique, ne peut être décomposé que d'une seule manière , en un certain nombre de vibrations pendulaires. [...] Il en résulte , par consééquent, que les considérations théoriques, par lesquelles les mathématiciens ont été amenés tout d'abord à ce mode de décomposition des vibrations composées, ont un fondement réel dans la nature des choses." Helmholtz, Théorie
Physiologique de la Musique (1863)
|
On lui doit la conception de résonateurs, sphériques à l'origine, parfois cylindriques comme dans les modèles ci-contre, construit par Rudolf Koenig (1832-1901) : chacun a sa fréquence propre de vibration, réagissant à la seule harmonique correspondante d'un son composé. Derrière l'appareil, pour chaque résonateur, une capsule manométrique réagit à la variation de pression, plus forte si le résonateur est sollicité par une harmonique correspondante, et agit sur le débit de gaz qui alimente une flamme; sur la droite de l'appareil, un prisme tournant, animé d'une rotation régulière, permet de visulaiser la hauteur de flamme en fonction du temps. C'est donc l'un des premiers analyseurs de Fourier construit, et il est dédié au son! |
|
|
Analyseur de Koenig, avec 14
résonateurs de Helmholtz
(Musée d'Histoire Naturelle, Lille) |
|
"Ces
vibrations composantes du mouvement de l'air, se manifestent donc comme
exerçant une action dans le monde extérieur,
indépendamment de l'oreille et de la théorie
mathématique.Il
en résulte , par conséquent, que les considérations
théoriques, par
lesquelles les mathématiciens ont été
amenés tout d'abord à ce mode de
décomposition des vibrations composées, ont un
fondement réel dans la
nature des choses."
Helmholtz, Théorie
Physiologique de la Musique (1863)
|
| "L'étude
approfondie de la nature est est la source la plus féconde
des
découvertes mathématiques.
Non
seulement cette étude, en offrant aux recherches un but
déterminé, a l'avantage d'exclure les questions
vagues et
les calculs sans issue; elle est encore un moyen assuré de
former l'analyse elle-même, et d'en découvrir les
éléments qu'il nous importe le plus de
connaître,
et que cette science doit toujours conserver: ces
éléments fondamentaux sont ceux qui se
reproduisent dans
tous les effets naturels." Fourier, Discours Préliminaire
à la Théorie Analytique de
la Chaleur
(1822)
|
Les Débuts de la Synthèse
Koenig est probablement le premier à avoir réalisé à la fois des instruments mécaniques d'analyse et de synthèse harmonique. Helmholtz a décrit au début de son livre des sirènes, dont le son est produit par un disque perforé tournant dans un flux d'air soufflé. Le modèle réalisé par Koenig sculpte le son grâce à son bord... qui est le graphe d'un polynôme trigonométrique, enroulé sur le bord du disque -périodicité garantie. Sans doute n'y a-t-il que 3 termes... mais qui peut dire mieux, en matière d'antériorité?|
|
||
| description de sirènes dans le traité d'Helmholtz | disque d'une sirène
conçue par Koenig (Musée d'Histoire Naturelle, Lille) |
|
Aujourd'hui, synthétiser se fait avec un... synthétiseur. Mais avant?
D'abord, l'instrument acoustique poussant le plus loin le principe de synthèse harmonique est l'orgue. Il suscite l'intérêt théorique de ... Mersenne et Bernoulli, comme par hasard. Et, ô surprise, voyez qui, en 1865, est responsable du rapport sur la rénovation de l'orgue de Saint Sulpice, à Paris!
|
|
||
| orgue de la Frauenkirche, Dresde (Allemagne) | St Sulpice: rapport de Lissajous, son tableau des possibilités combinatoires | |
Néanmoins, s'il réalise, par sa mécanique de tirettes, l'utilisation simultanée de plusieurs tuyaux, il faut bien remarquer qu'il s'agit d'une synthèse de sons dont chacun est déjà composé: aucun tuyau n'émet un son pur, sinusoïdal.
Or, un synthétiseur de sons sinusoïdaux a bel et bien existé, avant l'époque des circuits intégrés, dès le temps héroïque des amplis à lampes: c'est l'orgue Hammond, conçu en 1934, dont le modèle phare B3, a fait les belles heures des églises baptistes et des petits combos jazz des années 1950-60. Avec son pivot central "The Incredible" Jimmy Smith: tendez une petite oreille (et un petit oeil) à Organ Grinder's Swing avec Kenny Burrell à la guitare, pour vous remettre en mémoire les cordes vibrantes à la Gibson, ou le non moins emblématique Midnight Special. Avant, il y a Milt Buckner et Wild Bill Davis, après, en digne fils spirituel, le jeune et bouillant Joey de Francesco (un excellent concert en compagnie de David Sanborn au sax alto)...
|
|
|
| Jimmy Smith... Nice, jardins de Cimiez, 16 Juillet 1993, 23h |
... et son B3, ventre ouvert
pour aérer les tubes! (c'est chaud, Nice,
l'été... )
Nice, jardins de Cimiez, 15
Juillet 1983, 18h
|
L'idée géniale est de construire tous les sons à partir d'une sinusoïde pure par excellence: celle du courant secteur (60Hz aux USA). Au dessus de chaque touche, des tirettes (bien visibles sur le Midnight Special recommandé, et encore mieux avec Joey de Francesco -le clavier est souvent filmé en gros plan) permettent d'ajouter à chaque son des harmoniques choisies, chacune avec 8 possibiltés de niveau différentes! C'est donc la mise en œuvre exacte de la synthèse de Fourier, l'instrument qui est le plus proche de sa théorie! Après quoi, vous n'oserez plus jamais prétendre que Fourier, ça ne swingue pas...
Analyse et Synthèse: d'autres Machines Extraordinaires!L'ampleur des
calculs
nécessités par
l'évaluation des coefficients
de Fourier, ainsi que leur caractère fastidieux, ont
fortement
motivé la recherche d'une automatisation -dans un premier
temps,
une mécanisation- de ces calculs.
Un premier et magnifique exemple
est celui des calculateurs de marées de Lord
Kelvin:
vous pouvez vous y rendre sans plus attendre puisqu'il s'agit seulement
de manipuler des polynômes trigonométriques et non
des
séries; une machine effectue l'analyse, une autre la
synthèse.
Un second, tout
aussi fascinant, est une machine construite en 1897 par Albert Michelson (le
célèbre physicien de l'expérience éponyme,
démontrant l'invariance de la vitesse de la
lumière): elle peut effectuer à
elle-seule l'analyse et et la synthèse!
Son fonctionnement est présenté en
détails dans cette excellente préesntation
vidéo de Bill Hammack:Cette
première machine
peut sommer 20 termes, ou calculer 20 coefficients de Fourier; mais
fort de son succès, Michelson put obtenir les financements
pour
en construire une à 80 termes dès
l'année
suivante. Machine avec laquelle, grâce aux graphes
tracés,
il a peut-être pris conscience de ce que l'on appelle le phénomène
de Gibbs..En tout cas, il a suscité
l'intervention et la clarification donnée par Gibbs. Il n'était
que... le second, mais l'article premier, publié en en 1848
par Henry Wilbraham, était
passé inaperçu en dépit de sa
clarté.
|
"Ce n'est pas de la Musique, c'est du Bruit !!! "
Que de fois cet anathème n'aura-t-il pas été lancé! Beethoven, Berlioz, Stravinski ou Varèse en savent quelque chose, leur seule faute étant d'avoir écrit de la musique contemporaine (étonnant, non?) et même pire: en avance sur leur temps.Mais disposons nous d'un critère objectif et scientifique pour distinguer les deux? Déjà, Helmholtz tente de répondre, toutefois assez lucide pour affirmer le caractère flou et subjectif de la frontière:
|
"La
première et la plus importante différence entre
les
impressions auditives, est celle qui existe entre les bruits et les
sons musicaux.
Le
bourdonnement, le gémissement, le sifflement du vent, le
murmure
de l'eau, le roulement d'une voiture sur le pavé, sont des
exemples de la première espèce de sensation
auditive, les
sons de tous les instruments de musique donnent l'exemple de la seconde
espèce. Le son et le bruit peuvent, il est vrai, s'associer
dans
des rapports très variables, et se
confondre dans la transition de l'un à l'autre, mais les
extrêmes sont très nettement
séparées. [...]
Une sensation musicale apparait à l'oreille comme un son parfaitement calme, uniforme et invariable. [...] Il lui correspond, par conséquent, une sensation simple d'une nature régulière, tandis que, dans un bruit, de nombreuses sensations auditives sont irrégulièrement mélangées, et se heurtent l'une à l'autre. On peut effectivement composer un bruit avec des sons, par exemple, en frapppant à la fois les touches d'un piano comprises dnas l'étendue d'une ou deux octaves. D'après cela, il est évident que les sons musicaux constituent les éléments simples et réguliers des sensations auditives. " Helmholtz, Théorie
Physiologique de la Musique (1863)
|
Et à une extrême, justement, il y a le bruit blanc, souvent utilisé par les acousticiens pour faire des mesures pratiques, qu'il s'agisse de qualité des salles de concert ou d'isolation phonique des logements. Il s'agit d'une émission sonore où toutes les fréquences sont présentes, (presque) au même niveau. Le ressenti à l'oreille est un bruit totalement neutre (alors que le bruit de la mer, ou celui d'une salle de concert pendant que le public s'installe, fournissent à l'oreille assez d'éléments pour les distinguer, et les identifier: il y a mélange, excès de fréquences entendues, certes, mais les inégalités de leurs amplitudes permettent de les typer).
Pourquoi blanc, au fait? Par analogie avec la décomposition de la lumière blanche, réussie par Newton à l'aide d'un prisme: tout le spectre des longueurs d'onde audible est présent dans l'un comme tout le spectre des radiations visibles dans l'autre! C'est d'ailleurs Newton qui emploie le premier ce mot dans une lettre à Oldenburg (19/02/1672) et l'officialise dans son Optique (1704)
|
|
|
| Spectre d'un bruit blanc,
visualisation dans le logiciel Audacity: les fréquences sont en abcisses, leurs intensités en ordonnée. Elles sont toutes là! |
Newton séparant la
lumière blanche
(National Galery of Portraits,
Londres)
|
Sur la vie du mot spectre en physique, puis en mathématiques, on pourra consulter cet article de J. Mawhin; autre agréable introduction (où l'on reparle de cordes vibrantes...), celui de San Vu Ngoc sur le site Images des Mathématiques (CNRS). Si, en mathématiques, le spectre désigne aujourd'hui l'ensemble des valeurs propres, il le doit justement aux modes propres de vibration!
La Musique des Spectres
Un courant de musique du XXème siècle, né vers 1970, a fait de l'étude fine du son par son spectre un principe de base pour la composition; et de l'analyse par ordinateur un outil fondamental. Le son comme matériau avait déjà suscité l'intérêt de deux grands maîtres de cette époque, Olivier Messiaen, et, plus encore, Edgard Varèse, le premier à mêler électronique et instruments habituels dans sa scandaleuse (à l'époque) et célébrissime (aujourd'hui) partition, Déserts (1954). Mais c'était encore trop tôt pour tirer parti de l'ordinateur. La génération suivante arrive au bon moment: en janvier 1973, les compositeurs Tristan Murail, Michaël Lévinas et Roger Tessier, qui viennent de se rencontrer à la Villa Médicis, fondent un ensemble, L'Itinéraire, dédié à la création contemporaine. Ils sont rapidement rejoints par Hugues Dufourt et Gérard Grisey. Un courant, qui est aussi une alternative au sérialisme en vogue, voit le jour: celui de la musique spectrale, expression forgée par Hugues Dufourt. Sollicité par l'auteur de ces lignes pour apporter son soutien à l'érection d'une nouvelle statue de Fourier à Auxerre, Hugues Dufourt lui a fait la surprise d'offrir, pour les 250 ans de Fourier, un texte ample et original sur ce qui le lie à Fourier: vous pouvez le télécharger ici.|
En outre, en utilisant des sonogrammes, qui déploient la musique selon deux axes, lle temps (horizontalement) et les fréquences (verticalement), l'intensité dans chaque composante étant marquée par le niveau de gris, ils ont été pionniers (avant les mathématiciens!) des atomes temps-fréquences si essentiels dans la théorie de l'analyse multirésolution... qui n'est autre qu'un des remarquables prolongements de l'analyse de Fourier! voir notre page sur les ondelettes. |
|
|
sonogramme d'un Do 130Hz, suivi d'un Sol 200Hz, joués sur un alto. source: ce document, qui présente la musique spectrale. |
Remarque: quand la Physique permet d'éviter (temporairement) les douloureux problèmes de Mathématiques:
| Notre oreille est limitée: nous ne percevons
les fréquences qu'entre 20Hz et 20000Hz. Il en résulte que pour elle, toute série (somme infinie d'harmoniques) se réduit physiologiquement à une somme finie. Alors, tous les problèmes mathématiquement ardus:
Cette remarque peut vous aider (si vos connaissances mathématiques n'ent sont pas encore là...) à faire temporairement comme si ces difficultés n'existaient pas, en lisant la théorie de Fourier. Ne soyez pas dupe, il faudra y revenir... un peu plus tard, mais ce n'est pas une raison pour se priver du plaisir de parcourir cet ouvrage exceptionnel. |
Fourier et les Ondes: la Musique ne s'arrête pas là!
Au terme de cette introduction, vous devez pouvoir (l'auteur l'espère) aborder plus facilement notre lecture commentée de la Théorie Analytique de la Chaleur. À moins que vous ne préfériez poursuivre en musique! Mais comme il y aura un peu plus d'équations, nous y avons consacré une page distincte. N'ayez pas peur pour autant, ce sera avec modération! Et vous n'allez quand même pas passer à côté de liens vers d'excellents concerts... allez, un petit sommaire pour vous allécher:| Pourquoi
les Tambours sont-ils circulaires? |
Quelles équations pour les cymbales? | My Favourite
Things... (Clarinette ou Sax Soprano?) |
|
|
||
|
Buddy Rich, ou comment mener un
big band à la baguette...
(ex1 : Love for Sale; ex 2: West Side Story) Nice, arènes de
Cimiez, 13 Juillet 1986, 19h
|
Elvin Jones (et sa Jazz Machine)
Nice, jardins de Cimiez, 15
Juillet 1993, 19h
|
John Coltrane Capture d'écran, lien vers la vidéo dans la page suivante. |
Le Mathouriste n'oublie pas sa
promesse initiale; c'est dans cette deuxième page que la
résolution du problème clarinette vs sax soprano
sera traitée.
Et elle est maintenant disponible, avec des suppléments surprise!
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Aller à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformée de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique
Revenir
à la Home
Page du
Mathouriste
Et elle est maintenant disponible, avec des suppléments surprise!
Références Spécifiques à cette Page
- Dave BENSON, Music: a Mathematical Offering (version en ligne, 2008)
- Dave BENSON, Music: a Mathematical Offering (Cambridge University Press); page web du livre.
- B. ESCUDIE, C. GAZANHES, H. TACHOIRE, V. TORRA, Des Cordes aux Ondelettes (Presses de l'Université de Provence)
- C. GABRIEL, Cours d'Acoustique (téléchargeable par chapitres), ,notamment chap 4 (instruments) et chap. 11 (acoustique musicale et gammmes)
- Cours du Groupe Spécialisé d'Acoustique Musicale
- Liens du Groupe Spécialisé d'Acoustique Musicale
- B. HAMMACK, S.KRANZ, B. CARPENTER, Albert Michelson's Harmonic Analyzer (version PDF en ligne)
- H. HELMHOLTZ, Théorie Physiologique de la Musique (Masson)
- Lord RAYLEIGH, The Theory of Sound (Dover): en ligne: vol 1 , vol 2
- B.H. SUITS, Physics of Music, Notes (cours en ligne)
Poursuivre...
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Aller à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformée de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique