D'Alembert à Paris
Pauvre d'Alembert! Paris
n'a conservé aucune trace, ni de son lieu de naissance, ni
de sa sépulture:
"D'Alembert fut
exposé quelques heures après sa naissance, le 17
novembre
1717, sur les marches de l'église Saint-Jean-Lerond.
Cette petite église, démolie en 1748,... avait été une chapelle dépendant de la cathédrale ou, pour parler plus exactement, le baptistère même de Notre-Dame de Paris, accolé à la gauche de la façade"
C'est ainsi que Joseph Bertrand commence sa biographie. Enfant naturel (comme on disait alors) du chevalier Destouches et de Mme de Tencin, il avait été abandonné sur le perron d'une église, procédé bien classique... recueilli et confié à l’hospice des Enfants Trouvés, il y fut baptisé Jean Le Rond, en mémoire du lieu où il avait été découvert -procédé non moins classique..
A son décès, le 29 Octobre 1783, l'enterrement à l'église lui fut refusé -séquelle d'une polémique contre les jésuites ; l'anonymat de sa sépulture assura sa disparition ultérieure.
Précisément, à l'angle Place de l'Hôtel de Ville - Rue de Rivoli, Premier étage.
Situation générale
Un génie des Lumières... plutôt dans l'ombre!
Le collège (aujourd'hui siège de l’Académie française), et sa cour avec le cadran solaire double.
Chambres et salles de cours donnaient sur cet espace; ainsi professeurs et élèves avaient l'heure!
Pour s'en tenir à l'essentiel mathématique d'une
œuvre scientifique importante (incluant Physique et
Astronomie), on signalera:
- l'étude de l'équation des Cordes Vibrantes, par laquelle il fonde (1747) la théorie des Équations aux Dérivées Partielles et se montre précurseur de l'Analyse Harmonique: la célèbre controverse avec Daniel Bernoulli et Euler trouvera sa résolution dans la théorie de Fourier... en 1807. Pour plus de détails, notamment une analyse commentée des principaux textes, c'est ici, dans notre page introductive à l'analyse de Fourier.
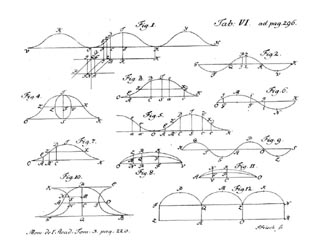
Début des deux premières livraisons, et une page de figure (Liens vers le texte intégral ci-dessous)
- les articles mathématiques de l'Encyclopédie: certes, notre homme s'y montre plus habile compilateur que véritable novateur; mais il faut aussi à la science des gens ayant le talent, qui n'est pas donné à tous, de synthétiser les connaissances de leur temps. S'il fallait lui faire un reproche, ce serait plutôt de ne pas citer ses sources! Son article sur les séries, par exemple ne fait guère que recopier Euler... Il délégue également certains sujets à ses collaborateurs; on sait ainsi que c'est Condorcet qui se chargea de l'article fractions continues.
Soulignons, pour le porter à son crédit, le
souci, complètement novateur, d'intégrer les
avancées les plus récentes; ainsi,
en liaison
avec le théorème précédent,
le fabuleux constructeur d'équations mis au point en 1761
par Janos Segner (la rédaction de l'Encyclopédie
s'étale de 1751 à 1772).
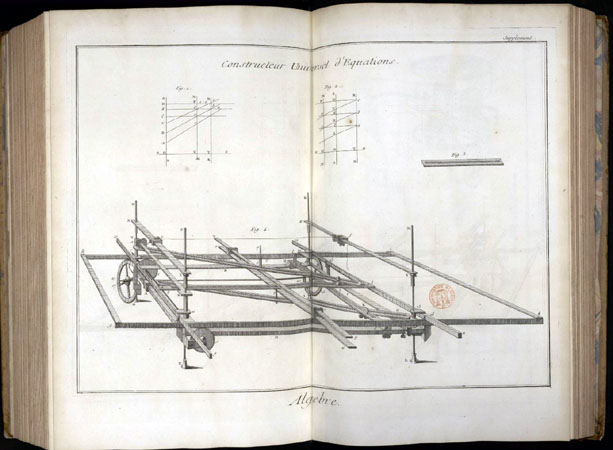
Pour savoir en quoi c'est une merveille informatique, visitez notre page dédiée en cliquant sur l'image!
La statue de Condorcet à Paris, non loin de l'Institut
Texte intégral du discours de Condorcet, in Mémoires Historiques, Littéraires et Anecdotiques du Baron de Grimm (1814)
Cette petite église, démolie en 1748,... avait été une chapelle dépendant de la cathédrale ou, pour parler plus exactement, le baptistère même de Notre-Dame de Paris, accolé à la gauche de la façade"
C'est ainsi que Joseph Bertrand commence sa biographie. Enfant naturel (comme on disait alors) du chevalier Destouches et de Mme de Tencin, il avait été abandonné sur le perron d'une église, procédé bien classique... recueilli et confié à l’hospice des Enfants Trouvés, il y fut baptisé Jean Le Rond, en mémoire du lieu où il avait été découvert -procédé non moins classique..
A son décès, le 29 Octobre 1783, l'enterrement à l'église lui fut refusé -séquelle d'une polémique contre les jésuites ; l'anonymat de sa sépulture assura sa disparition ultérieure.
La Mémoire de Paris...
Malgré cela, Paris se souvient de d'Alembert: on peut y voir deux statues qui le représentent. La première sur la façade de l'Hôtel de Ville:
Précisément, à l'angle Place de l'Hôtel de Ville - Rue de Rivoli, Premier étage.
Situation générale
Un génie des Lumières... plutôt dans l'ombre!
Deuxième
rencontre au Louvre, département des sculptures
françaises.
L'œuvre,
réalisée
par le sculpteur Félix Lecomte (1737-1817) est une commande
antérieure à 1786. Napoléon en fit don
à
l'Institut. Le respect des lois du genre et de l'époque est
à noter dans les détails:
Eh oui! À
ses pieds, le brouillon du Discours Préliminaire
à l'Encyclopédie -une vue
"retournée" de 180° en attestera.
Contraste forcé pour faire ressortir le trait.
Contraste forcé pour faire ressortir le trait.
Des portraits en peinture
existent
également en région Parisienne; trois au moins.
L'un est situé dans la salle des
séances de l'Institut (aile Lebas)
-hélas, non ouverte aux visiteurs lors des
Journées du Patrimoine... En voici deux autres (informations
supplémentaires en cliquant sur les miniatures):
 |
 |
| par Catherine Lusurier (1777) Musée Carnavalet, Paris |
par Quentin La Tour (1753) Musée du Louvre, Paris |
Un ouvrage d'A. Gasté (1896), disponible
en ligne a d'ailleurs été consacré
à ce second portrait.
Et puis, il a une place dans la gigantesque fresque de Raoul Dufy, la Fée Électricité, peinte en 1937 et exposée en permanence au Musée d'Art Moderne de la Ville de Paris: le premier à étudier l'équation des ondes, il ne pouvait que la mériter!
Parmi les "théoriciens" de l'électricité. À sa gauche, De Borda.
Et puis, il a une place dans la gigantesque fresque de Raoul Dufy, la Fée Électricité, peinte en 1937 et exposée en permanence au Musée d'Art Moderne de la Ville de Paris: le premier à étudier l'équation des ondes, il ne pouvait que la mériter!
Parmi les "théoriciens" de l'électricité. À sa gauche, De Borda.
Le Mathématicien et l'Encyclopédiste
Mathématicien, ce fut la première vocation de D'Alembert! C'est dans cette discipline qu'il se signale par un premier travail à l'Académie des Sciences en 1739: il a alors 22 ans. Il avait fait préalablement de fort brillantes études au collège janséniste des Quatre-Nations , car son père, s'il ne l'avait pas reconnu, avait veillé à lui assurer des ressources et une bonne éducation. Il y fut inscrit d'abord sous le nom de Darembert, changé ensuite en D'Alembert.
Le collège (aujourd'hui siège de l’Académie française), et sa cour avec le cadran solaire double.
Chambres et salles de cours donnaient sur cet espace; ainsi professeurs et élèves avaient l'heure!
- l'étude de l'équation des Cordes Vibrantes, par laquelle il fonde (1747) la théorie des Équations aux Dérivées Partielles et se montre précurseur de l'Analyse Harmonique: la célèbre controverse avec Daniel Bernoulli et Euler trouvera sa résolution dans la théorie de Fourier... en 1807. Pour plus de détails, notamment une analyse commentée des principaux textes, c'est ici, dans notre page introductive à l'analyse de Fourier.
Début des deux premières livraisons, et une page de figure (Liens vers le texte intégral ci-dessous)
- le théorème
fondamental de l'Algèbre: si la manie
française de dénommer Théorème
de d'Alembert ce qui ne sera pas complètement
éclairci avant Gauss peut (légitimement!) agacer,
on ne saurait pour autant occulter son rôle ni ses efforts.
Il est l'un des maillons importants de la longue chaîne de
ceux qui, depuis la première formulation de Descartes
dans la
Géométrie
(1637), "labourent le terrain" dans lequel Gauss
n'aura
plus qu'à semer en réexaminant les lacunes de ses
prédécesseurs, qu'ils s'appellent
Euler,d'Alembert, Lagrange
ou Laplace...
Gauss ne commence-t-il pas son
mémoire en disant:
"On doit la première démonstration du théorème à l'illustre géométre d'Alembert, Recherches sur le Calcul Intégral, Histoire de l'Académie de Berlin, Année 1746, pp 182 et suivantes" ?
Les deux premières pages du mémoire...
et le moment crucial où apparait le fameux énoncé, dans toute sa clarté.
"On doit la première démonstration du théorème à l'illustre géométre d'Alembert, Recherches sur le Calcul Intégral, Histoire de l'Académie de Berlin, Année 1746, pp 182 et suivantes" ?
Les deux premières pages du mémoire...
et le moment crucial où apparait le fameux énoncé, dans toute sa clarté.
- les articles mathématiques de l'Encyclopédie: certes, notre homme s'y montre plus habile compilateur que véritable novateur; mais il faut aussi à la science des gens ayant le talent, qui n'est pas donné à tous, de synthétiser les connaissances de leur temps. S'il fallait lui faire un reproche, ce serait plutôt de ne pas citer ses sources! Son article sur les séries, par exemple ne fait guère que recopier Euler... Il délégue également certains sujets à ses collaborateurs; on sait ainsi que c'est Condorcet qui se chargea de l'article fractions continues.
Pour savoir en quoi c'est une merveille informatique, visitez notre page dédiée en cliquant sur l'image!
Hommage posthume
Son éloge
posthume à l'Institut fut dit par son
protégé -et légataire- Condorcet,
qui
enchaina sur celui d'Euler, disparu à quelques semaines
d'intervalle.
La statue de Condorcet à Paris, non loin de l'Institut
Texte intégral du discours de Condorcet, in Mémoires Historiques, Littéraires et Anecdotiques du Baron de Grimm (1814)
 |
 |
| Lors de l'exposition inaugurale du Louvre-Lens (2012/13), une rencontre aussi unique qu'insolite:la statue de D'Alembert devant le célèbre tableau d'Eugène Delacroix, La Liberté guidant le Peuple. |
Liens
Biographies
- Sur Wikipédia
- à l'Université St-Andrews
- Par Joseph Bertrand (en ligne, Projet Gutenberg)
- Biographie et nombreux liens sur un site consacré à Voltaire.
Œuvres
- Mémoire sur les Cordes Vibrantes, en ligne à l'Académie de Berlin: partie 1, partie 2, supplément.
- L' Encyclopédie ... en ligne!
- Ou encore ici, avec ses Planches, et d'autres œuvres numérisées (Gallica, Académie de Berlin)
- Discours de réception à l'Académie Française (19/12/1754)
- Site de l'édition des Œuvres Complètes , en ligne (Académie des Sciences) incluant:
- Œuvres Mathématiques: avant 1756, après 1756
- Articles de l'Encyclopédie
- Correspondance: D'Alembert en Toutes Lettres.
Livres et Revues
- Le numéro 39 des Génies de la Science (Mai-Juillet 2009): voir le sommaire en ligne ; conçu par P. Crepel.
- C, ALVAREZ, J. DHOMBRES, Une Histoire de l'Imaginaire Mathématique: Vers le Théorème fondamental de l'Algèbre et sa Démonstration par Laplace en 1795 (Hermann)
- C, ALVAREZ, J. DHOMBRES, Une Histoire de l'Invention Mathématique: Les démonstrations du Théorème fondamental de l'Algèbredans le Cadre de l'Analyse... de Gauss à Liouville. (Hermann)
- C, ALVAREZ, J. DHOMBRES, Une Histoire de ...: Troisième et dernier volet, à paraître (Hermann)
- B.FINE, G. ROSENBERGER, The Fundalmental Theorem of Algebra (Springer)
- R. REMERT , The Fundalmental Theorem of Algebra in H.D. EBBINGHAUS & alias, Numbers (Springer)
Documents en ligne
- Un dossier thématique Jean Le Rond d'Alembert sur le site Image des Mathématiques (CNRS), avec notamment ces articles:
- G. Jouve, D’Alembert et les Équations aux Dérivées Partielles
- P. Pansu, La Lumière et les Ondes
- P. Crepel, Application des Probabilités à la Médecine
- P. Crepel, D'Alembert doute-t-il de tout?
- Un dossier d'Alembert sur le site de Culture-Maths, coordonné par P. Crépel, avec notamment des liens et ces articles:
- P. Crepel, Qu’y a-t-il de nouveau dans l’oeuvre scientifique de D’Alembert?
- P. Crepel, Les dernières perfidies de D'Alembert
- Michel Paty D’Alembert et les Probabilités
- Ondes sur une Corde Vibrante sur Wikipédia
- Equation des Ondes sur Wikipédia (actuellement plus complet et mieux illustré en Anglais qu'en Français...), incluant la solution de d'Alembert.
- G. JOUVE, Imprévus et Pièges des Cordes Vibrantes chez D'Alembert, thèse (2007)
Revenir
à la Home
Page du
Mathouriste