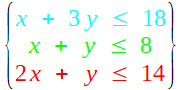Quand Fourier inventait l'Optimisation Linéaire...
... avec plus d'un siècle d'avance!
Fourier est souvent présenté
comme l'homme d'un seul problème: la diffusion de la chaleur, et d'un
seul livre, par lequel il révolutionne les mathématiques pour les deux
siècles à venir, forgeant deux outils majeurs: les séries de Fourier, et la transformation de Fourier, laquelle, dans sa version rapide, la FFT (Fast Fourier Transform) figure dans le top ten des algorithmes (liste, article par Barry Cipra) les plus utilisés. Or...
Deux algorithmes sur les dix plus grands de l'histoire, ça vous pose un homme d'exception, non? Certes, comme la FFT est l'œuvre de Cooley et Tuckey, le "simplexe", comme on le nomme en raccourci est en toute légitmité signé Dantzig. Fourier était trop en avance sur son temps: l'ordinateur n'existait pas. Mais l'idée pionnière était là; c'est ce que révèlent quelques papiers longtemps occultés par l'ombre portée de son volumineux ouvrage sur la chaleur.
Pour aborder ses textes, et pour mieux les saisir, il sera bon de se familiariser avec le type de problèmes traités sur des exemples simples. Alors, avant de découvrir Fourier, un peu de patience! Elle sera récompensée en faisant la balade avec un accompagnateur d'exception: Alberto Giacometti.
Un ingénieur passe l'essentiel de son temps à résoudre des problèmes d'optimisation sous contraintes; et pour tout arranger, celles-ci revêtent souvent des aspects contradictoires. Ainsi, un véhicule spatial devra emporter le plus possible de matériel pour sa mission, tout en étant le plus léger possible... sans parler de l' encombreùent! Un problème d'optimisation est la recherche du meilleur (ou plutôt, souvent, du moins mauvais) compromis. Il se décompose donc, grossièrement, en deux parties:
La classe de problèmes étudiée par Fourier et Dantzig est heureusement plus simple; et toute cette simplicité est dans l'adjectif linéaire, dernier mot à commenter. Cela siginife que contraintes et fonction à optimiser seront du premier degré en les variables. Avec 3 variables par exemple, x, y, z, les contraintes devront être de la forme
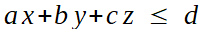 ou
ou 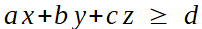
et la fonction à maximiser ou minimiser est
et même si cela peut sembler très réducteur, beaucoup de situations concrètes peuvent être modélisées de la sorte.

Deux Problèmes Modèles
On donne encore le nom de simplexe à ce domaine.
Et si vous préférez étudier l'affaire avec des produits bien concrets, n'hésitez pas à visiter cette présentation de nos amis belges, pour qui, bien sîur, la question fondamentale est de savoir si l'on va fabriquer de la bière blonde ou de la bière brune... ( à partir de maïs, de houblon et de malt) Dilemme du brasseur, comme on le nomme parfois.
Deux remarques sur les modèles:
Évidemment, ceus que nous venons d'écrire peuvent sembler totalement irréalistes, naïfs... le but était d'obtenir une illustration graphique claire; et pour cela, ne pas avoir à gérer trop de variables (ni trop de contraintes) était capital. Mais le problème du régime avait été formulé, dans la publication de Stigler, en 1945, avec 77 denrées et 9 nutriments! Quant à la source de question, il faut la chercher dans la définition des rations alimentaires de l'armée U.S.
Un autre sujet d'importance; touchant à l'effort de guerre fut celui du mélange des carburants. Donnons en un exemple, une fois de plus hypersimplifié... mais aussi la version "grandeur nature"originale: le problème comportait 10 containtes et 22 inconnues.
Et celui de 1824 , que nous présenterons plus loin, témoigne d'avancées importante .
Et maintenant, on optimise!
Retour aux Problèmes Modèles: la Vision Géométrique
Introduisons dans nos modèles la fonction à optimiser, souvent dénommée, pour des raisons évidentes, fonction économique.
Oui, mais... quand il y aura un grand nombre de variables, ce ne sera pas aussi facile. Voyons ce qu'en disent, d'une part Fourier en 1823, et d'autre part un des plus célèbres informaticiens de notre temps, inventeur des arbres bicolores, Robert Sedgewick, dans son best-seller Algorithms, où il consacre un chapitre à l'algorithme du simplexe;
Incroyable..., non? (Et chacun avec, à côté de lui, une partie de sa bibliothèque...) Même la généralisation avec des contraintes non linéaires est évoquée de part et d'autre!
Le plaisir de la sculpture, c'est de tourner autour... ici, c'est bien le cas de dire: l'explorer sous toutes ses faces!
Cette œuvre va apporter à l'exposé de Fourier, dans l'Histoire des Travaux qu'il présente à l'Académie en 1824, la figure qui manque à ce résumé. On dirait que Fourier reprend la suite d'un feuilleton commencé l'année précédente, continuant à évoquer un mystérieux Mémoire que nous regrettons de ne pas posséder.
En voici, illustrés et commentés, les passages les plus remarquables.

Fourier pose alors son problème comme recherche des valeurs qui réalisent le minimum d'une fonction (voire plusieurs!) dont il vient de nous rappeler qu'elle est linéaire en les inconnues.

L'ordre est matérialisé par la succession des couleurs de l'arc en ciel.

Mais cela arrive enfin, sans trop de détails par manque de place, nous prévient-il. Aussi allons nous expliciter sa démarche sur le problème (P), en la comparant à la version "clasique" de Dantzig. Certes, il y a des différences, et s'il s'agit de l'implémenter sur ordinateur, la version de Dantzig, appuyée sur l'agèbre linéaire (tout simplement pas encore inventée à l'époque de Fourier, l'emporte sans discussion. Il n'empêche: il y beaucoup de point commun, en particulier le recours à l'élimination.
Peut-être aurez-vous remarqué une certaine ambiguïté dans le texte de Fourier: après avoir introduit , x, y, z, ... comme variables, c'est z qu'il cherche à minimiser. Cela va s'éclairer ici, par "l'astuce" du rajout d'une contrainte.
Fourier conclut à la généralité de sa méthode, insistant sur le fait que son Mémoire contient toutes les démonstrations.

Robert Sedgewick, on l'a mentionné plus haut, avait dès la première édition (1983, s'appuyant sur le langage Pascal) de son traité Algorithms, réservé un chapitre à la programmation linéaire; aux côtés de la FFT, dans la section intitulée Sujets Avancés. L'autre grand traité qui, comme celui de Sedgewick, domine les 40 dernières années de l'informatique générale, l'Introduction à l'Algorithmique de Cormen, Leiserson & Rivest a attendu sa 2ème édition (2001) pour ajouter l'indispensable chapitre sur ce sujet, preuve d'une actualité jamais démentie au tournant du troisième millénaire.
L'étude des équations est un sujet qui occupe toute la carrière de Fourier, de son premier article soumis à l'Académie à la préparation de ce traité en deux tomes, que sa mort laisse réduit, tel une symphonie inachevée, à ce seul premier mouvement. Soit une période nettement plus longue que la célébrissimme Théorie Analytique de la Chaleur! Très documentée en témoignages de première main, l'introduction rédigée par Henri Navier éclaire sur le projet d'ensemble et l'état d'achèvement.
"Nous allons indiquer..." Effectivement, Il poursuit en développant... mais c'est une recopie, quasiment mot pour mot (!), des résumés historiques de 1823 et 1824 que Darboux a regroupés avec la Solution d'une Question particulière du Calcul des Inégalités,... bref, rien de nouveau, pas la moindre information supplémentaire. Impossible, à ce stade, de resserrer le domaine réalisable (si l'on ose dire) d'apparition de ce sujet.
La situation est plus claire dans la résurgence au XXème siècle, mais il faut parler là de réinvention et non d'héritage: alors ignoré, le travail de Fourier ne sera redécouvert qu'a posteriori.
Son traité a été publié plusieurs fois, en versions successivement augmentées... mais nous ne saurions trop conseiller la version princeps, Linear Programming, Theory and Extensions (Princeton 1963), beaucoup plus riche sur l'histoire de cette découverte. Elle se trouve sûrement dans de nombreuses bibliothèques (mais peut-être plus du côté des sciences économiques que des mathématiques)
Dantzig lui-même était légèrement précédé... par des mathématiciens ne connaissant pas davantage, à cette époque, l'antériorité de Fourier! Remontons un peu le temps:
1941 : Hitchcock et le Problème du Transport
Dantzig le présente sur un schéma très paralant!
Il y a certes antériorité de publication (Dantzig était contraint au sevcret pendant la période de guerre), mais d'une part, la vue est moins large, moins générale que celle de Dantzig, et d'autre part, elle a fait l'objet d'une méthode dédiée spécifique, la méthode hongroise (par référence à son inventeur, Kuhn).
N.B. : Ce n'est pas, loin de là, le seul des problèmes-modèles "historiques" à pouvoir être résolu par le simplexe, tout en bénéficiant , par sa spécificité, d'algorithmes spécialisés, plus efficaces dans ce cas précis. Ainsi le célèbre problème du sac à dos: il s'agit
Mais ce qui le complique énormément, c'est que les variables ne peuvent prendre que les valeurs 0 ou 1. En tout cas, la plupart du temps, lorsque les articles ne sont pas fractionnables: pour une randonnée, est-ce que j'emporte ou non la boîte de cassoulet? C'est un cas de programmation en nombres entiers, dont voici en exemple plus général:: Si je fais de la contrebande de cartouches de cigarettes de 3 marques A, B, C (exemple choisi pour être réaliste,en matière de contrebande montagnarde...), les variables x, y, z ne peuvent prendre que des valeurs entières, et l'optimum en nombres entiers n'est pas toujours proche de l'optimum en variables réelles, que trouverait rapidement l'algorithme du simplexe...
Programmes linéaires, certes, mais qui justifieront des algorithmes spécifiques: malgré sa versatlité, sa puissance, et sa robuste simplicité, l'agorithme de Dantzig ne peut pas tout!
En savoir plus sur le problème du sac à dos: article d'initiation sur le site Interstices, article Wikipedia.
1939 : Leonid Kantorovitch
Petit avertissement aux candidats à la lecture d'un ouvrage de Kantorovitch: c'est le genre de gars qui vous traite en 3 à 4 pages la programmation linéaire que d'autres auteurs mettent (avec la plus grande pertinence) un livre entier à préseenter aux étudiants...
La question de la rencontre entre économie et programmation linéaire
C'est à dire: que se passe-t-il avant Kantorovitch et Koopmans?
N.B: Wassily Leontieff (1905-1999, né Russe, naturalisé Américain) a obtenu le Prix Nobel d'économie en 1973; son inspiration mathématique doit beaucoup à Andreï Markov (1856-1922.
La question de l'efficacité, #2: point de vue algorithmique
Le mieux est, là encore, d'abord de rendre la parole à Dantzig:
La question de la linéarité (ou non)
Peut-on aller plus loin? Une fonction-objectif non linéaire? Des contraintes non-linéaires? Les deux?
Sur un cas aussi "visuel" que notre problème modèle (P), conserver le mêm domaine et considérer un autre type de fonction-objectif n'est pas difficile: il s'agit seulement de changer de type de courbes de niveau. Ainsi, avec:
Mais... Fourier l'avait dit avant lui, en conclusion du texte de 1824!

Soyons honnête: la conclusion paraît un peu trop optimiste... si la convexité est souvent présente dans les problèmes d'optimisation non linéaires, les techniques en sont tout de même très différentes, et sortent du cadre de cette page. Ceux qui voudraient découvrir le sujet peuvent consulter, en première approche, le petit Que sais-je de Jean-Baptiste Hirriart-Urruty, L'Optimisation (PUF 1996).
Références
Un autre algorithme dont Fourier est le précurseur figure dans cette liste : l'algorithme du simplexe de George B. Dantzig.
Deux algorithmes sur les dix plus grands de l'histoire, ça vous pose un homme d'exception, non? Certes, comme la FFT est l'œuvre de Cooley et Tuckey, le "simplexe", comme on le nomme en raccourci est en toute légitmité signé Dantzig. Fourier était trop en avance sur son temps: l'ordinateur n'existait pas. Mais l'idée pionnière était là; c'est ce que révèlent quelques papiers longtemps occultés par l'ombre portée de son volumineux ouvrage sur la chaleur.
Pour aborder ses textes, et pour mieux les saisir, il sera bon de se familiariser avec le type de problèmes traités sur des exemples simples. Alors, avant de découvrir Fourier, un peu de patience! Elle sera récompensée en faisant la balade avec un accompagnateur d'exception: Alberto Giacometti.
 Alberto Giacometti et Jacques Dupin (montré à l'exposition au Centre Pompidou, 2007-2008) |
Non,
Giacometti n'a pas travaillé la terre pour modeler le visage d'un
Fourier prenant la pose, nonchalamment appuyé sur une chaise... L'image de gauche est tirée d'un film sur le sculpteur. À droite: - buste de Fourier, par Nacéra Kaïnou, présenté dans plusieurs expositions commémorant les 250 ans du grand mathématicien et physicien en 2018, notamment à l'IHP (Paris) et au Museum d'Auxerre. - portrait de Fourier par Claude Gautherot, daté de l'an XI (1802-1803), retrouvé au musée d'Auxerre... en 2018, justement! Alors, qu'est-ce qui rapproche Giacometti et Fourier? Lisez cette page pour savoir! |
Optimisation Linéaire : Quésaco?
Vocabulaire : n'ayons pas Peur!
Optimiser sous contraintes, ce qui est l'objet de cette page, tout le monde le fait, mais de façon informelle. Optimiser est le mot choisi pour englober Maximiser et Minimiser, sans devoir préciser à chaque fois ce qui est pour nous optimal: si M et Mme Jourdain sont vendeurs, ils chercheront certainement à maximiser leur bénéfice; si Mme et M Jourdain sont acheteurs, à minimiser leurs dépenses. Des contraintes... tout le monde en a, n'est-ce pas? En faisant nos courses, nous sommes limités par le volume de notre sac, le poids qu'il peut supporter... et, pour la plupart d'entre nous, notre budget.Un ingénieur passe l'essentiel de son temps à résoudre des problèmes d'optimisation sous contraintes; et pour tout arranger, celles-ci revêtent souvent des aspects contradictoires. Ainsi, un véhicule spatial devra emporter le plus possible de matériel pour sa mission, tout en étant le plus léger possible... sans parler de l' encombreùent! Un problème d'optimisation est la recherche du meilleur (ou plutôt, souvent, du moins mauvais) compromis. Il se décompose donc, grossièrement, en deux parties:
- définition précise et caractérisation de l'ensemble des solutions possibles (le domaine réalisable);
- détermination (algorithmique) d'une ou plusieurs "meilleures solutions" parmi celles-ci.
La classe de problèmes étudiée par Fourier et Dantzig est heureusement plus simple; et toute cette simplicité est dans l'adjectif linéaire, dernier mot à commenter. Cela siginife que contraintes et fonction à optimiser seront du premier degré en les variables. Avec 3 variables par exemple, x, y, z, les contraintes devront être de la forme
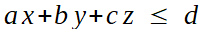 ou
ou 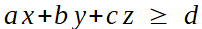
u x + v y + w z
et même si cela peut sembler très réducteur, beaucoup de situations concrètes peuvent être modélisées de la sorte.

Il sera toutefois plus clair
d'aborder la question avec quelques exemples-modèles plus classiques
dans les présentations modernes du sujet.
Deux Problèmes Modèles
| Problème de Production (P) | Problème du Régime Équilibré (R) | ||||||||||||||
Prenant 1 comme gain par tonne de P1 produite, et donc 2 par tonne de P2 produite, le bénéfice total s'exprime par z = x + 2 y
(si le bénéfice unitaire sur P1 était b , on obtiendrait z = b(x + 2 y) , ce qui ne changerait rien au problème...) Gardons nous de dire : puisque P2 rapporte plus, ne produisons que P2 ! Il est vorace en M1, et il est évident qu'on ne pourra alors en produire que 6 tonnes (qui consommeront les 6×3t = 18t de M1). Le bénéfice serait alors 6×2 = 12. On va bien voir si on peut faire mieux! Formons mainteant les contraintes, qui résultent de la disponibilité en matières premières. x tonnes de P1 requièrent x tonnes de M1 , y tonnes de P2 requièrent 3y tonnes de M1 , la consommation totale est x + 3 y , et elle doit rester inférieure à 18 (quantité disponible)
On traite de même M2 et M3 ; on obtient donc l'ensemble de contraintes :(les deux contraintes évidentes :x>0 , y>0 ny sont pas écrites pour alléger) |
Les contraintes résultent ici de la réalisation d'un apport minimum;
par exemple, l'apport en V est 1 x + 5 y , et il doit être au moins 5, ce qui se traduit par x + 5 y ≥ 5
Les deux autres s'écrivent de même... et voici notre problème: |
||||||||||||||
Or, une bonne fée nous suggère x = 3, y = 5 : cela vérifie les contraintes, et alors z = 13: c'est mieux que précédemment! Mais peut-on toujours attendre les fées? Peut-on chercher en aveugle, au petit bonheur? Il est temps de regarder géométriquement le problème. Chacune des inéquations définit une région du plan, définie par une droite, facile à construire: la première passe par les points (18 , 0) et (0 , 6) : ce sont les points d'intersection avec les axes. On a représenté la droite dans la couleur de l'inéquation correspondante. 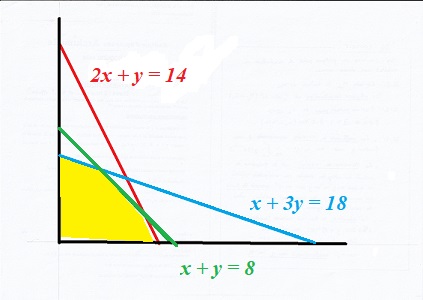 Les contraintes définissent un domaine (en jaune) dit domaine réalisable:
c'est l'ensemble des points du plan vérifiant toutes les inégalités.
C'est la surface interne à un polygone convexe; tout point de ce
domaine est un schéma de production acceptable.
Cela ne nous dit pas encore quel est "le meilleur"... mais patience! Nous y viendrons. |
Il n'y a plus qu'à construire, comme ci-contre, les trois droites définissant les inégalités pour obtenir le domaine réalisable. 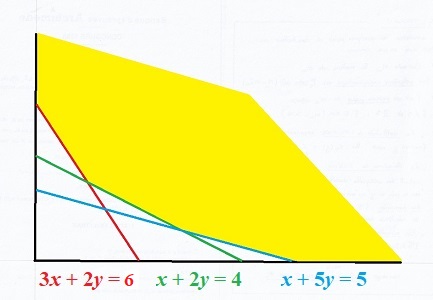
Les contraintes définissent un domaine (en jaune) dit domaine réalisable:
c'est l'ensemble des points du plan vérifiant toutes les inégalités. Il
est dans ce cas la surface illimitée au dessus de la ligne polygonale;
il est encore convexe; et tout point de ce
domaine est un menu acceptable.
La différence la plus notable est que le domaine est, cette fois, non borné. Mais il est toujours convexe. |
On donne encore le nom de simplexe à ce domaine.
Et si vous préférez étudier l'affaire avec des produits bien concrets, n'hésitez pas à visiter cette présentation de nos amis belges, pour qui, bien sîur, la question fondamentale est de savoir si l'on va fabriquer de la bière blonde ou de la bière brune... ( à partir de maïs, de houblon et de malt) Dilemme du brasseur, comme on le nomme parfois.
Deux remarques sur les modèles:
Évidemment, ceus que nous venons d'écrire peuvent sembler totalement irréalistes, naïfs... le but était d'obtenir une illustration graphique claire; et pour cela, ne pas avoir à gérer trop de variables (ni trop de contraintes) était capital. Mais le problème du régime avait été formulé, dans la publication de Stigler, en 1945, avec 77 denrées et 9 nutriments! Quant à la source de question, il faut la chercher dans la définition des rations alimentaires de l'armée U.S.
Un autre sujet d'importance; touchant à l'effort de guerre fut celui du mélange des carburants. Donnons en un exemple, une fois de plus hypersimplifié... mais aussi la version "grandeur nature"originale: le problème comportait 10 containtes et 22 inconnues.
|
Exprimant toutes les quantités en m3 , ce problème s'écrit :
|
Simplifions mathématiquement, sans rien changer: on peut écrire, en multipliant par 10
|
||
| Autrment dit: c'est exactement le même problème que (R) ! Deux problèmes dans des contextes très différents,...
... pour un seul modèle mathématique: c'est toute la puissance de la modélisation! |
À ce stade, nous en savons assez pour lire un premier article de Fourier!
Un Petit Article de notre Grand Joseph
Il est le seul connu de Fourier sur ce thème, en 3 petites pages auxquelles Darboux, éditeur des œuvres "complètes" (qui ne le sont probablement pas...). Commençant par ces mots:"La question suivante offre une application du calcul des inégalités [...] "
il confirme l'idée que Fourier a déjà écrit
plus généralement sur le sujet. Les délais de publication de l'Académie
ajoutent à l'imbroglio, puisqu'on a vu le compte-rendu de 1823 édité
seulement... en 1827.Et celui de 1824 , que nous présenterons plus loin, témoigne d'avancées importante .
| Le problème posé a 3 inconnues, x, y, z, positives, liées par la relation x + y + z = 1 et vérifiant les inégalités écrites ci-dessous à gauche. Elles son transcrites à droite après substitution de z = 1 - x - y ; se ramèner à deux variables x, y et permet ainsi l'interprétation graphique dans le plan: par exemple, [1] x < z ( 1 + r ) devient x < ( 1 - x - y ) ( 1 + r ) , et on réordonne. |
||
| [1] x < z ( 1 + r ) [2] z < x ( 1 + r ) [3] y < z ( 1 + r ) [4] z < y ( 1 + r ) [5] x < y ( 1 + r ) [6] y < x ( 1 + r ) |
[1] ( 2 + r ) x + ( 1 + r ) y < ( 1 + r ) [2] ( 2 + r ) x + y > 1 [3] ( 1 + r ) x + ( 2 + r ) y < ( 1 + r ) [4] x + ( 2 + r ) y > 1 [5] x < y ( 1 + r ) [6] y < x ( 1 + r ) |
|
| La figure de Fourier peut paraître énigmatique -nul ne contestera, du moins l'espérons nous, son esthétique! Il n'a, en effet, écrit aucune équation, mais, à la place, donné des constructions géométriques équivalentes. Et pour commencer, il faut disposer nos axes (en violet épais)... d'une façon fort inhabituelle! On construit un carré de côté 1 (violet) et petits carrés de côté r (l'un est en évidence, en marron, en bas à droite) |
||
|
|
Pour y voir plus clair, tournons la figure vers la gauche d'un quart de tour : ainsi, les axes sont dans la position où nous avons l'habitude de les représenter. Nous pouvons alors reconnaître les droites frontières pour les condition [1] à [6] : [1] ( 2 + r ) x + ( 1 + r ) y = ( 1 + r ) car elle passe par les points m' (0,1) et a' (1 + r , -1 - r ) [2] ( 2 + r ) x + y = 1 car elle passe par les points m' (0,1) et b' (1 , -1 - r ) [3] ( 1 + r ) x + ( 2 + r ) y = ( 1 + r ) car elle passe par les points m" (1,0) et b" ( -1 - r , 1+ r ) [4] x + ( 2 + r ) y = 1 car elle passe par les points m" (1,0) et a" ( -1 - r , 1 ) Les deux dernières, issues de l'origine, ont un tracé évident [5] x = y ( 1 + r )
Le domaine réalisable (simplexe) est alors l'intérieur du petit hexagone (irrégulier, précise Fourier) qu'il note 123456. Et, vous le constatez sûrement, il n'est ici question que de décrire le domaine réalisable: pas de fonction à maximiser ou minimiser! Mais Fourier en parle ailleurs... |
Et maintenant, on optimise!
Retour aux Problèmes Modèles: la Vision Géométrique
Introduisons dans nos modèles la fonction à optimiser, souvent dénommée, pour des raisons évidentes, fonction économique. | Problème de Production (P) | Problème du Régime Équilibré (R) |
|
Il s'agit ici de maximiser z = x + 2 y
Elle garde une valeur constante, égale à h, sur toute la droite x + 2 y = h
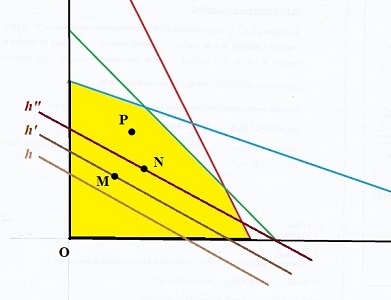
qui peut donc être qualifiée de ligne de niveau de la fonction économique. Comme sur une carte de randonneur, nous avons tracé quelques-unes de ces lignes de niveau, pour les niveaux successifs h < h' < h"
La ligne de niveau se déplace parallèlement à elle-même, "montant" lorsque h croît. Considérons un point intérieur au domaine réalisable (non situé sur une des droites qui le bordent), M sur la figure. On peut, à l'évidence, en se déplaçant dans le sens des h croissants, se placer sur une ligne d'un niveau h" supérieur à h' , en N par exemple.: M n'est pas optimal. On peut, la plupart du temps, trouver un point où la fonction économique a une valeur plus grande par un petit déplacement horizontal ou vertical. Le maximum n'est jamais atteint à l'intérieur du domaine réalisable.
C'est un peu moins évident, mais encore faisable, sur un segment du bord: prenons par exemple CD, et regardons ses intersections avec les courbes de niveau: il y a un des deux sens de parcours à partir du point où la valeur de la fonction augmente (on croise des courbes de niveau h plus grand). Le maximum n'est (en général) pas atteint sur une arête de bord.
Il y a un cas exceptionnel... nous vous le laissons deviner (indication: essayez la fonction économique z = 2 x + 2 y ) Il est donc atteint en un sommet.
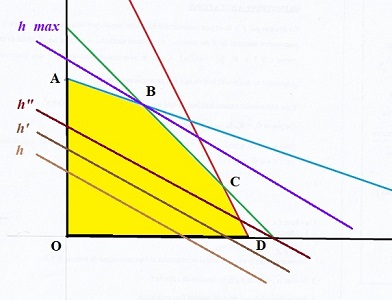
Ici, il s'agit clairement de B. De "quelque côté que l'on se tourne", sur BC, sur BA, impossible de faire mieux que le niveau h_max de la droite violette: les parallèles pour un h plus grand se situent hors du domaine réalisable. On peut d'ailleurs, ici, énumérer les sommets : O, A , B , C, D , y calculer les valeurs et vérifier lequel est le meilleur. Oui, mais... |
Rappelons que le le but est de minimiser la fonction
z = 20 x + 25 y
Elle garde une valeur constante, égale à h, sur toute la droite 20 x + 25 y = h
qui peut donc être qualifiée de ligne de niveau de la fonction économique. Comme sur une carte de randonneur, nous avons tracé quelques-unes de ces lignes de niveau, pour les niveaux successifs h < h' < h"
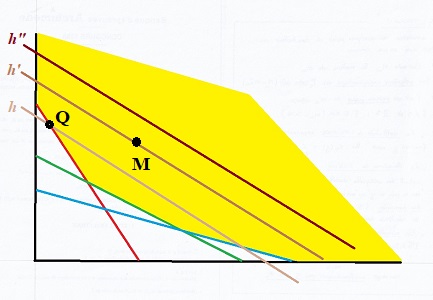 La ligne de niveau se déplace parallèlement à elle-même, "montant" lorsque h croît. En un point intérieur au domaine réalisable (non situé sur une des droites qui le bordent), M sur laligne de niveau h', on peut, à l'évidence, en se déplaçant dans le sens des h décroissants, se placer sur une ligne d'un niveau h inférieur à h'.: M n'est pas optimal. On peut,trouver un point où la fonction économique a une valeur plus petite par un petit déplacement horizontal ou vertical. Le maximum n'est jamais atteint à l'intérieur du domaine réalisable.
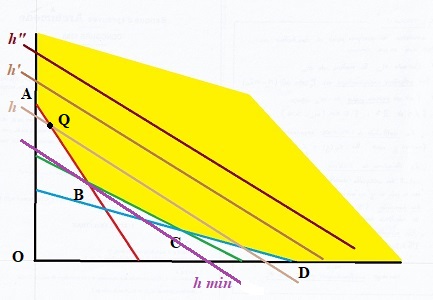 Sur
un segment du
bord, on peut encore, dans la plupart des cas, trouver en choisissant
un sens de parcours convenable,se déplacer vers une courbes de niveau,
représentative d'un niveau plus faible. Ainsi, à partir du
point Q de AB, on peut diminuer la valeur de la fonction en "descendant" vers B.
Le minimum n'est (en général) pas atteint sur une arête de bord.
Il est donc atteint en un sommet.
Ici, il s'agit clairement de B. De "quelque côté que l'on se tourne", sur BC, sur BA, impossible de faire mieux (c'est à dire moins!) que le niveau h_min de la droite violette: les parallèles pour un h plus grand se situent hors du domaine réalisable. On peut d'ailleurs, ici, énumérer les sommets : O, A , B , C, D , y calculer les valeurs et vérifier lequel est le meilleur. Oui, mais... |
Oui, mais... quand il y aura un grand nombre de variables, ce ne sera pas aussi facile. Voyons ce qu'en disent, d'une part Fourier en 1823, et d'autre part un des plus célèbres informaticiens de notre temps, inventeur des arbres bicolores, Robert Sedgewick, dans son best-seller Algorithms, où il consacre un chapitre à l'algorithme du simplexe;
 |  |
|
"Il
faut insister sur un point : bien que ces phénomènes soient faciles à
voir quand il n'y a que deux variables et peu d'inégalités, ils
deviennent nettement moins perceptibles dans un problème plus général avec beaucoup de variables et d'inégalités.[...]
Si les inégalités étaient non linéaires, le simplexe pourrait avoir une forme géométrique bien moins triviale. [...] Quoi qu'il en soit, l'intuition géométrique est précieuse, car elle aide à comprendre les caractéristiques fondamentales de la méthode de base utilisée en pratique pour résoudre des problèmes de mdimension supérieure." R. Sedgewick, Algorithmes en Langage C, trad. française J.M. Moreau (Interéditions 1991)
image : wikipedia |  |
Incroyable..., non? (Et chacun avec, à côté de lui, une partie de sa bibliothèque...) Même la généralisation avec des contraintes non linéaires est évoquée de part et d'autre!
Fourier optimise Géométriquement... du Grand Art!
En 3 dimensions, le simplexe est bordé par un polyèdre irrégulier, avec des faces (chacune définie par une équation de plan), des arêtes (intersections de deux plans), des sommets (intersections de trois plans), comme on peut en découvrir un bel exemple... mais oui! Là -bas, derrière la table, au fond, contre le mur... |
 |  |
| L'atelier d'Alberto Giacometti (reconstitué). Fondation Giacometti, Paris |
||
| Mais oui, dans l'atelier d'Alberto Giacometti! Cette sculpture, malicieusement intitulée "Le Cube",
a été conçue en 1933-34, dans sa période surréaliste (de quoi expliquer
son titre...), ne cache guère sa référence au polyèdre de la non moins
célèbre Melancolia (1514) de Dürer, reproduite sur le timbre ci-contre: le graveur allemand, féru de mathématiques, y combinait des éléments géométriques (le polyèdre, la sphère) et arithmétiques (le carré magique).
|
|||
 |
Le "cube" de Giacometti a
12 faces, contre 8 au polyèdre de Dürer; il en existe des versions en
plâtre (dont une au Centre Pompidou, voir sa fiche incluant une analyse), mais aussi en bronze, notamment à la Fondation Maeght (Saint-Paul de Vence), où le Mathouriste a, pour la première fois, rencontré les statues du sculpteur... quel choc!
|
||
| Le Cube, modèle en bronze. Rétrospective 2019 au LaM, Musée d'Art Moderne de Villeneuve d'Ascq (Nord) |
|||
Le plaisir de la sculpture, c'est de tourner autour... ici, c'est bien le cas de dire: l'explorer sous toutes ses faces!
 |
 |  |
| Exposition Picasso-Giacometti, 2016, au Musée Picasso (Paris) | ||
Cette œuvre va apporter à l'exposé de Fourier, dans l'Histoire des Travaux qu'il présente à l'Académie en 1824, la figure qui manque à ce résumé. On dirait que Fourier reprend la suite d'un feuilleton commencé l'année précédente, continuant à évoquer un mystérieux Mémoire que nous regrettons de ne pas posséder.
En voici, illustrés et commentés, les passages les plus remarquables.

Fourier pose alors son problème comme recherche des valeurs qui réalisent le minimum d'une fonction (voire plusieurs!) dont il vient de nous rappeler qu'elle est linéaire en les inconnues.

 |
Oui, vous l'avez bien lu: le mot-clef, le mot visionnaire, est ici algorithmique. Quand le nombre d'inconnues est trop grand pour que l'observation géométrique apporte directement la solution (comme dans nos problèmes-modèles à deux variables), il faut disposer de règles algorithmiques sûres pour opérer sans voir directement. Manipuler le simplexe sans le voir, comme la femme manipule, dans la sculpture de Giacometti, l'objet invisible... |
||
|
L'Objet Invisible (1934-35)
À gauche: au LaM, Musée d'Art Moderne de Villeneuve d'Ascq (Nord), Rétrospective 2019également visible en permanence à la Fondation Maeght, Saint Paul de Vence (Alpes Maritimes). À droite: un autre exemplaire se trouve au MOMA de New York (USA) |
|||
| Mais attention, rappelons nous ce qu'a
écrit Sedgewick: cet algorithme doit être guidé par l'intuition
géométrique, et c'est ce que Fourier va exposer, et où "Le Cube" nous offrira la figure qui manque à son article. | |||
|
Et c'est parti! Le décor, pour commencer...
 |  |
| L'algorithme consiste à rejoindre, à partir d'un point quelconque, d'abord une arête, puis un sommet du polyèdre : | |
 |
 |
| Ainsi, l'algorithme fait cheminer de sommet en sommet, comme en suivant les arêtes... |
L'ordre est matérialisé par la succession des couleurs de l'arc en ciel.
 |
 |  |
|
Le cas de la sculpture, telle qu'elle est présentée, est un peu particulier: son appui sur une face fait qu'il n'y a pas unicité du sommet minimisant... ce qui peut parfaitement se produire dans la réalité:
|  |
 |
Si l'on renversait l'image à 180°, le minimum serait unique, ou,
cela revient au même, si on suit un tel algorithme pour rechercher le
maximum. La figure est très intéressante à ce point de vue, car cette
fois, le maximum est unique, mais l'algorithme, qui demande de monter
de sommet en sommet, offre plusieurs choix possibles en H : un même but, des
routes différentes.
Ces routes se rejoignent en K, avant d'emprunter l'arête sommitale vers S. |
|
 |
|
|
| Giacometti, Homme qui marche (circa 1960). Fondation Giacometti, Paris | ||
De la Géométrie à l'Algorithme Algébrique
Fourier conclut sa présentation géométrique en martelant, une nouvelle fois, que c'est ainsi que se déroulent les opérations, selon une règle analytique (comprendre: l'algorithme des calculs)... dont il n'a toujours pas soufflé mot.
Mais cela arrive enfin, sans trop de détails par manque de place, nous prévient-il. Aussi allons nous expliciter sa démarche sur le problème (P), en la comparant à la version "clasique" de Dantzig. Certes, il y a des différences, et s'il s'agit de l'implémenter sur ordinateur, la version de Dantzig, appuyée sur l'agèbre linéaire (tout simplement pas encore inventée à l'époque de Fourier, l'emporte sans discussion. Il n'empêche: il y beaucoup de point commun, en particulier le recours à l'élimination.
Peut-être aurez-vous remarqué une certaine ambiguïté dans le texte de Fourier: après avoir introduit , x, y, z, ... comme variables, c'est z qu'il cherche à minimiser. Cela va s'éclairer ici, par "l'astuce" du rajout d'une contrainte.
| (P) , méthode de Fourier | (P) , méthode de Dantzig |
|
l'idée :
 la préparation :
On reformule ainsi la question de maximisation:, en remplaçant max ( z = x + 2 y )
z ≤ x + 2 y , max ( z )
C'est astucieux, en ce sens qu'au maximum, il y aura nécessairement égalité; sinon, on pourrait encore augmenter un peu z... Le système de contraintes s'écrit alors (avec des inégalités toutes de même sens, pour pouvoir les additionner, à l'occasion multipliées par un nombre positif) [0] - x - 2 y + z ≤ 0 [1] x + 3 y ≤ 18 [2] x + y ≤ 8 [3] 2 x + y ≤ 14 |
l'idée :
Trois nouvelles variables positives (autant que de contraintes) sont introduites : u , v, w . [1] x + 3 y + u = 18 [2] x + y + v = 8 [3] 2 x + y + w = 14 max ( z = x + 2 y + 0 u + 0 v + 0 w )
Elles indiquent l'écart (d'où leur nom) , mesuré en "niveau" (au sens de l'étude graphique) entre la consommation dûe à la combinaison courante de produits et le stock de matière première disponible. Ainsi, au point C (6,2) de la figure, u = 18 - 6 -3×2 = 6 représente la quantité de M1 restante, tandis que v = 0 et v = 0 signalent l'épuisement des srocks de et . On dit alors, suggestivement, que ces deux contraintes sont serrées. Cependant, z = 6+2×2 = 10: on peut mieux faire... autrement. Du point de vue algébrique, ce système à 3 équations et 5 inconnues est clairement indéterminé, de rang 3, ce qui signifie que, dans la plupart des cas (formulation volontairement laissée un peu lâche!); fixant arbitrairement 2 inconnues -par exemple x et y- on peut tirer les 3 autres. Plus précisément, l'écrivant sous forme de combinaison de vecteurs colonnes à composantes) x C1 + y C2 + u C3 + v C4 + w C5 = S
[ C1 a pour composantes 1,1,2 ; S a pour composantes 18,8,4 ; etc ....] ce qu'on a dit est exact, parce que ( C3 , C4 , C5 ) est une base de l'espace de dimension 3. L'algorithme va consister à changer de base, pour améliorer le score z. Pour améliorer le bénéfice, mettons du produit P2 dans notre schéma de production, choix dicté par sa haute rentabilité. Nous allons donc faire entrer le vecteur C2 dans la base... très bien, mais il faut que quelqu'un sorte pour luii faire place, car une base de ℝ3 comporte exactement 3 vecteurs: la dimension est, par définition, le nombre de vecteurs d'une base. Alors, qui sort? Nous pouvons produire P2 à concurrence de ce que permettent les inégalités: 3 y ≤ 18 , y ≤ 8, y ≤ 14
Cest donc la première qui nous limite, en l'occurence par y ≤ 6; prendre y = 6, en saturant la contrainte, exige d'annuler d'office x et u . Le schéma de production provisoirement le meilleur est ( x = 0 , y = 6, u = 0 , v = 2 , w = 8 )
Aussi, c'est C3 qui va céder sa place pour que la solution s'exprime sur une base.Observons enfin que ( x = 0 , y = 6 ) est le point A du simplexe; c'est général: on peut montrer qu'à toute base réalisable correspond un sommet du simplexe.
Aller de base en base (en échangeant un vecteur à chaque opération) est
la manière algébrique d' "aller de sommet en sommet en suivant une
arête" de la vision géométrique. |
| l'élimination : Fourier nous indique la marche: on va éliminer x de [1], [2], [3], grâce à [0] |
l'élimination : Avec la nouvelle base ( C2 , C4 , C5
) nous voulons mettre le système sous une forme "résolue en les
variables de base", ou, pour le dire autrement, une forme où les
variables d'écart sont y, v , w . Ainsi, nous serons en mesure de poursuivre, de la même manière, le processus d'amélioration.
C'est ici la variable y que l'on va éliminer des équations (mais on aurait travaillé avec x si l'on avait choisi d'introduire d'abord une production de P1 ).
La technique est souvent dénommée méthode du pivot de Gauss, mais nul
besoin d'être érudit pour la pratiquer sur un cas simple comme le nôtre!
|
| Action! [0], avec [1], nous fournit - 2 y + z ≤ x ≤ 18 - 3 y
d'où - 2 y + z ≤ 18 - 3 y
c'est à dire: s'il existe un tel x, on a cette nouvelle inégalité; mais inversement, si elle est réalisée, on peut intercaler un x entre les deux membres (éventuellement égal, s'il advenait que la nouvelle inégalité soit une égalité pour les valeurs de y et z qui seront déterminées ultérieurement.On réécrit tout en réduisant, pour ne laisser qu'une constante à droite de , de façon à réitérer le processus. On remplace de la même manière [2] par [2] + [0] , [3] par [3] + 2 [0] ; on a : [0] - x - 2 y + z ≤ 0 [1'] y + z ≤ 18 [2'] - y + z ≤ 8 [3'] - 3y + 2z ≤ 14 On a éliminé x : il ne figure plus dans le système d'inégalités obtenues [1'], [2'], [3']. |
Action! On divise [1] par 3 : [1'] 1/3 x + y + 1/3 u = 6 (équation -pivot) et on reporte, pour que y ne figure plus dans les autres équations. On forme ainsi [2'] = [2] - [1'] et [3'] = [3] - [1']
[1'] 1/3 x + y + 1/3 u = 6 [2'] 2/3 x - 1/3 u + v = 2 [3'] 5/3 x - 1/3 u + w = 14 max ( z = 12 + 1/3 x - 2/3 u + 0 v + 0 w )
en ayant effectué le report également dans la fonction objectif. On a éliminé y : il ne figure plus dans le système des égalités restantes [2'] , [3']. |
la réitération et l'arrivée à l'optimum : C'est, cette fois [1'] "l'équation pivot", qu'on ajoute à [2'] d'une part,et [3'], d'une part: z - 8 ≤ y ≤ 18 - z 2z - 14 ≤ 3 y ≤ 54 - 3z [2"] 2 z ≤ 26, soit z ≤ 13 [3"] 5 z ≤ 68, soit z ≤ 13 + 3/5 La première est évidemment la plus contraignante, et l'on ne peut faire mieux que 13... on a retrouvé ainsi le résultat de l'optimisation graphique! |
la réitération et l'arrivée à l'optimum : Commençons par observer qu'introduire "un peu de u'" ne serait pas une bonne idée: cela ne pourrait que diminuer z; c'est ce que nous apprend le signe "-" devant u. Tout le contraire, le "+ 1/3 x " encourage à l'introduction de x comme variable de base, donc du vecteur C1 dans la base, avec la double question:
2/3 x ≤ 2 ; 5/3 x ≤ 14
La limitation vient de la première, avec x ≤ 3 : ce sont toutes les solutions réalisables restantes, et la valeur 3 est bien sûr optimale. C1 entre dans la base, et C4 en sort, car le choix x = 3 force v = 0 ; C4 est inutile. La base retenue est donc ( C1 , C2 , C5 ). Éliminant la variable x, grâce à qu'on écrit x = 3 + 1/2 u - 3/2 v
le but devient:max ( z = 13 - 1/2 u - 1/2 v + 0 w)
Tous les coefficients étant désormais négatifs ou nuls, une augmentation d'une variable ne peut que diminuer la valeur de z, ce qui démontre que sa valeur n'est plus améliorable. Aiutrement dit, nous avons là un critère d'optimalité. 13 est la valeur optimale, et elle est réalisée par ( x = 3 , y = 5, u = 0 , v = 0 , w = 3 ), c'est à dire au sommet B du graphique. |
Fourier conclut à la généralité de sa méthode, insistant sur le fait que son Mémoire contient toutes les démonstrations.

Robert Sedgewick, on l'a mentionné plus haut, avait dès la première édition (1983, s'appuyant sur le langage Pascal) de son traité Algorithms, réservé un chapitre à la programmation linéaire; aux côtés de la FFT, dans la section intitulée Sujets Avancés. L'autre grand traité qui, comme celui de Sedgewick, domine les 40 dernières années de l'informatique générale, l'Introduction à l'Algorithmique de Cormen, Leiserson & Rivest a attendu sa 2ème édition (2001) pour ajouter l'indispensable chapitre sur ce sujet, preuve d'une actualité jamais démentie au tournant du troisième millénaire.
Place dans l'Œuvre de Fourier
|
"Cette question des inégalités a beaucoup préoccupé Fourier ;
il avait l'intention de publier, dans son grand ouvrage sur la Théorie des Équations, une étude développée sur ce sujet." G. Darboux, Œuvres de Fourier, t.2. (Note sur les Mémoires présentés dans cette page)
|
||
 |
||
| Traité (posthume) de Fourier sur les Équations, édité par Navier; début de l'introduction rédigée par ce denier. | Buste de Navier (Ponts & Chaussées) |
|
L'étude des équations est un sujet qui occupe toute la carrière de Fourier, de son premier article soumis à l'Académie à la préparation de ce traité en deux tomes, que sa mort laisse réduit, tel une symphonie inachevée, à ce seul premier mouvement. Soit une période nettement plus longue que la célébrissimme Théorie Analytique de la Chaleur! Très documentée en témoignages de première main, l'introduction rédigée par Henri Navier éclaire sur le projet d'ensemble et l'état d'achèvement.
 | |
| ci-dessus : témoignage d'un élève polytechnicien, recueilli par Navier ci-contre : en épluchant la Décade Égyptienne, Navier trouve la trace de l'activité algébrique de Fourier à l'Institut du Caire.
|
S'ils nous révèlent un Fourier rompu aux méthodes algébriques, notamment l'élimination -très importante ci-dessus, on l'a vu, ils nous renseignent aussi, fût-ce avec une inévitable incertitude, par ce qu'ils ne disent pas: aucune trace de systèmes d'inégalités dans ces premières années de carrière. Sil s'en était occupé à cette époque, n'aurait-on pas au moins la mention d'une "lecture d'un mémoire sur les inégalités"?
|
Puis, Fourier prend la parole. Preuve de l'importance qu'il
accorde à cet ultime ouvrage, il y signe pas moins de trois textes
introductifs: une Préface, une Introduction (essentiellement historique), et un Exposé Synoptique, le plus précieux pour notre objet, puisqu'il y trace de façon très détaillée le contenu tout entier des deux volumes prévus. Cest ainsi qu'il nous annonce le sujet des inégalités... pour la toute fin de l'ouvrage. | |
 |
"Nous allons indiquer..." Effectivement, Il poursuit en développant... mais c'est une recopie, quasiment mot pour mot (!), des résumés historiques de 1823 et 1824 que Darboux a regroupés avec la Solution d'une Question particulière du Calcul des Inégalités,... bref, rien de nouveau, pas la moindre information supplémentaire. Impossible, à ce stade, de resserrer le domaine réalisable (si l'on ose dire) d'apparition de ce sujet.
Inspirateurs (???) et Successeurs
Optimiser n'a en soi rien de nouveau à l'époque de Fourier: des problèmes géométriques, au demeurant assez difficiles, ont été résolus grâce à la puissance du calcul différentiel: courbe brachystochrone (voir notre page Huygens), chaînette pesante et aux contributions décisives d'Euler et Lagrange. Mais il n'y aucun lien avec l'optimisation linéaire qui puisse suggérer une association d'idées.Simplexes dans le désert égyptien, près du Kaire (comme aurait écrit Fourier) |
Mentor de Fourier à l'École Normale, Monge,
qui l'avait recruté pour l'École Polytechnique, puis l'expédition
d'Égypte, s'était penché sur un problème devenu célèbre, celui des déblais et remblais (comment déplacer un tas de sable d'un endroit à un autre au moindre coût?), aujourd'hui dénommé problème du transport optimal de Monge-Kantorovich. Ils ont eu tout le temps d'en discuter en Égypte...
mais ce sujet est trop éloigné, lui aussi, de l'optimisation linéaire.
Affirmer que la contemplation, dans ce pays, de magnifiques simplexes
géants l'aurait inspiré serait aussi fantaisiste que de prétendre que
c'est le climat du pays qui lui a inspiré l'étude de la chaleur, ne
nous y risquons pas.Son activité de statisticien vers 1820? S'il évoque
bien comme application les probabilités et la "théorie des erreurs",
cela manque singulièrement de précision; la méthode des moindres carrés, introduite par Gauss (1801) et Legendre (1805)
s'est imposée en astronomie, sans rapport avec ce sujet. Bref, aucune
source d'inspiration claire ne se dégage, et Fourier, tout aussi
disert, en brossant l'histoire les travaux antérieurs, sur l'algèbre
que sur la chaleur, remonte à l'antiquité mais tait ce qui l'a fait
descendre dans l'arène.
| |
| Petit Complément Technique: Analyse des Erreurs et Optimisation Linéaire, ce qu'a peut-être fait Fourier Dissipons toute ambiguïté: rien, dans les articles de statistique édités par Darboux dans le Tome 2 des Œuvres de Fourier,
ne témoigne de l'utilisation du calcul des inégalités, au contraire, il
évoque les sommes des carrés des erreurs. À quoi, alors, fait il
allusion au début de l'article d'histoire de 1824, quand il parle
d'application à la Théorie des Erreurs?
Nous proposons ici, en l'absence de document le certifiant, ce qu nous semble le plus vraisemblable.
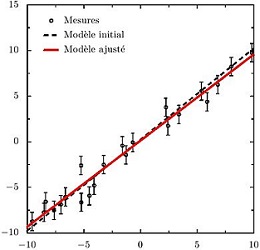
Mais une autre idée est tout aussi pertinente a priori: minimiser la somme des écarts en valeurs absolue, plutôt que leurs carrés, c'est à dire: | ax1 + b - y1 | + | ax2 + b - y2 | + ... + | axn + b - yn |
Ce n'est pas davantage linéaire, mais une petite transformation va y ramener. Le problème peut en effet s'écrire Min ( e1 + e2 + ... + en )
e1 ≥ | ax1 + b - y1 | , e2 ≥ | ax2 + b - y2 |, ... , en ≥ | axn + b - yn | en introduisant n nouvelles inconnues, e1 , e2 , ... , en . Il n'y a plus qu'à transformer chaque contrainte en une double inégalité pour avoir un programme linéaire; par exemple on écrit, pour remplacer la première: e1 ≥ ax1 + b - y1 et e1 ≥ - ( ax1 + b - y1 )
ce qui a pour effet de doubler le nombre d'inégalités, mais à ce prix, la forme d'un programme linéaire est obtenue. Voici les deux extraits des textes de Fourier qui nous donnent à penser que c'est bien ce dont il s'agit:  à la fin du de l'Histoire de l'Académie pour 1823 (Note 1 de Darboux dans les Œuvres, t.2)  dans l'Histoire de l'Académie pour 1824 (Note 2 de Darboux dans les Œuvres, t.2) |
La situation est plus claire dans la résurgence au XXème siècle, mais il faut parler là de réinvention et non d'héritage: alors ignoré, le travail de Fourier ne sera redécouvert qu'a posteriori.
1947 : George Bernard Dantzig
C'est lui qu'on a surnommé "Père de la Programmation Linéaire". 1947 est la date de l'article séminal, mais il avait développé sa méthode en travaillant au Pentagone de 1941 à 1945. Le mot Programmation ne faisait alors aucune référence à l'implémentation sur des ordinateurs... naissants, mais à l'idée d'une planification organisée (comme on le dit pour un cinéma, un théâtre, une salle de concerts... ou l'organisation de ses rendez-vous!); parler aujourd'hui d'Optimisation Linéaire permet d'éviter la confusion entre l'étude mathématique et sa traduction sur machine: rien ne vaut d'écouter les souvenirs du héros sur ce point... et sur le rôle de la Géométrie dans sa formation. Une influence sûrement décisive dans son inspiration! |
"J'avais
été engagé dans la Division de Contrôle Statistique.[...]. L' Air Force
ne disposait alors d'aucun système qui lui donne l'état de ses
appareils. Ils ne savaient même pas combien ils avaient d'avions, moins
d'une centaine à l'époque.[...] Je
devins un expert en méthodes d'organisation planifiée en utilisant
comme «machines de calcul» les seules alors disponibles: des machines
de bureau opérées par des humains. "
|
| "Des
maîtres influents? Oui, particulièrement Mr Gilbert, mon professeur de
mathématiques au lycée. C'est lui qui m'a appris la géométrie. La
Géométrie m'a vraiment branché. [...] La Géométrie Projective a été pour moi comme le lait maternel, pour citer Eliza dans le Pygmalion de G.B. Shaw. J'ai été élevé avec ça. Mon père me l'a apprise en me donnant des problèmes à résoudre quand j'étais au lycée. Il m'a donné des milliers, je devrais dire des centaines de milliers, de problèmes à résoudre. Dès que j'arrivais avec une solution, il me disait: «Bien, je vais t'en donner un autre.» [...]. Cet exercice mental est le plus grand cadeau que m'ait fait mon père." |
Son traité a été publié plusieurs fois, en versions successivement augmentées... mais nous ne saurions trop conseiller la version princeps, Linear Programming, Theory and Extensions (Princeton 1963), beaucoup plus riche sur l'histoire de cette découverte. Elle se trouve sûrement dans de nombreuses bibliothèques (mais peut-être plus du côté des sciences économiques que des mathématiques)
Dantzig lui-même était légèrement précédé... par des mathématiciens ne connaissant pas davantage, à cette époque, l'antériorité de Fourier! Remontons un peu le temps:
1941 : Hitchcock et le Problème du Transport
 |
Imaginez un pays fictif, bien organisé face à une épidémie galopante.
Il doit acheminer des vaccins de 2 dépôts vers 3 centres de
vaccination, tant qu'à faire au moindre coût (car son gouvernement est
soucieux de faire au mieux avec l'argent de ses contribuables, plutôt
que d'engager à prix d'or 7 cabinets de consultants pour 28 contrats).
Imaginez que son agence de santé ait, en poste à demeure, un
logisticien formé aux principes de la Recherche Opérationnelle
(discipline plus vaste, englobant des problèmes d'oprtimisation
combinatoire variés) plutôt qu'une chaise vide, et, à côté, une armée
mexicaine d'experts dirigée par un quarteron d'infectiologues en retraite... Imaginez, vous dis-je!
| |||||||||||||
| N.B.
: les informations relatives au pays réel de comparaison, que vous
pourriez avoir reconnu, figurent dans un article en première page du Canard Enchaîné daté du 17/02/21 |
| Sur la Route 66, du côté de Pontiac (Illinois)... |
présenté par Dantzig dans son livre de 1963: 3 points de départ, 5 d'arrivée |
|
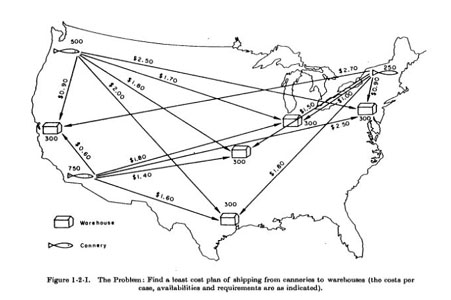 | ||
| Nougaro aurait dit: "C'est pas du Ronsard, c''est de l'Amerloque!" |
||
Il y a certes antériorité de publication (Dantzig était contraint au sevcret pendant la période de guerre), mais d'une part, la vue est moins large, moins générale que celle de Dantzig, et d'autre part, elle a fait l'objet d'une méthode dédiée spécifique, la méthode hongroise (par référence à son inventeur, Kuhn).
N.B. : Ce n'est pas, loin de là, le seul des problèmes-modèles "historiques" à pouvoir être résolu par le simplexe, tout en bénéficiant , par sa spécificité, d'algorithmes spécialisés, plus efficaces dans ce cas précis. Ainsi le célèbre problème du sac à dos: il s'agit
- d'optimiser la "valeur" (marchande, mais pas forcément: penser à
l'utilité, à condition de pouvoir lui attribuer une échelle de mesure)
du contenu d'un sac,
- sous la contrainte de ne pas dépasser un certain poids (ou un certain encombrement!).
a x + b y + c z ≤ K
Max ( u x +v y + w z )
Max ( u x +v y + w z )
Mais ce qui le complique énormément, c'est que les variables ne peuvent prendre que les valeurs 0 ou 1. En tout cas, la plupart du temps, lorsque les articles ne sont pas fractionnables: pour une randonnée, est-ce que j'emporte ou non la boîte de cassoulet? C'est un cas de programmation en nombres entiers, dont voici en exemple plus général:: Si je fais de la contrebande de cartouches de cigarettes de 3 marques A, B, C (exemple choisi pour être réaliste,en matière de contrebande montagnarde...), les variables x, y, z ne peuvent prendre que des valeurs entières, et l'optimum en nombres entiers n'est pas toujours proche de l'optimum en variables réelles, que trouverait rapidement l'algorithme du simplexe...
Programmes linéaires, certes, mais qui justifieront des algorithmes spécifiques: malgré sa versatlité, sa puissance, et sa robuste simplicité, l'agorithme de Dantzig ne peut pas tout!
| Poser son sac à dos... au pied d'un simplexe! (en Haute Maurienne, du côté de Val-Cenis) |
Le soir, deux amateurs de simplexe... |
||
En savoir plus sur le problème du sac à dos: article d'initiation sur le site Interstices, article Wikipedia.
1939 : Leonid Kantorovitch
 Portait par P. Vodkin (Source Wikimedia Commons) |
Fiche CIA de Kantoroich (Source Wikipedia Anglais) [ Un Russe, prix Nobel d'économie? Vite, faites moi une fiche sur lui!!! ] |
Son cas est bien
différent: il travaillait en URSS, où il a passé toute sa vie. Devenu
très jeune professeur d'université à Leningrad, il s'intéresse à la
planification et à l'optimisation, il conçoit, indépendamment des
américains, la programmation linéaire: ses ouvrages phares datent de
l'immédiat avant-guerre: Méthode mathématique de planification et d’organisation de la production (1939) et Allocation optimale des ressources économiques
(1939). Cette dernière question lui vaudra en 1975 un prix Nobel
d'économie, ...et une sympathique petite fiche dans une célèbre agence
étatsunienne. Il partageait le prix avec Koopmans,
mais, curieusement, Dantzig avait été "oublié" par le jury Nobel... si
l'on croit cette image au moment de la remise, il n'en voulait pas trop
aux deux récipiendaires.
| |
|
"En URSS en 1939, Kantorovitch fit des propositions qui furent négligées pendant les deux décennnies qui virent l'avénement de la programmation linéaire et sa solide implantation à peu près partout" G.B. Dantzig,
préface de Linear Programming & Extensions |
 |
||
|
|
|||
Petit avertissement aux candidats à la lecture d'un ouvrage de Kantorovitch: c'est le genre de gars qui vous traite en 3 à 4 pages la programmation linéaire que d'autres auteurs mettent (avec la plus grande pertinence) un livre entier à préseenter aux étudiants...
La question de la rencontre entre économie et programmation linéaire
C'est à dire: que se passe-t-il avant Kantorovitch et Koopmans? (source : Wikipedia)
|
"L'introduction actuelle de la programmation linaire en économie apparaît comme un anachronisme; il aurait été logique qu'elle débute autour de 1758, quand les économistes ont commencé à décrire les systèmes économiques en termes mathématiques. Et vraiment, on peut trouver un exemple grossier de programmation linéaire dans le Tableau Économique de Quesnay,
qui tentait de relier les rôles du propriétaire, du paysan et de
l'artisan. Walras a également proposé en 1874 un modèle mathématique
sophistiqué incluant des coefficients techniques fixes. Assez
singulièrement, cependant, les mmodèles linéaires furent peu exploités
avant les années 1930. [...]
La grande contribution de Leontieff, selon l'opinion de l'auteur, fut sa construction d'un modèle quantitatif de l'économie américaine. Pour apprécier la différence entre un modèle purement formel et un modèle empirique, il faut bien avoir en tête que la collecte des données pour un modèle réel réclame qu'une organisation y travaille des mois, voire des années. Après, un nouvel obstacle se présente: la solution d'un grand système d'équations linéaires simultanées. Dans les années 1936-1940, il n'y avait pas de calculateurs électroniques; le mieux qu'on pouvait espérer résoudre était un système de 20 équations à 20 inconnues." G.B. Dantzig, préface de Linear Programming and Extensions
|
N.B: Wassily Leontieff (1905-1999, né Russe, naturalisé Américain) a obtenu le Prix Nobel d'économie en 1973; son inspiration mathématique doit beaucoup à Andreï Markov (1856-1922.
La question de l'efficacité, #1: avis sur la méthode
|
" Le test ultime d'une théorie, c'est sa capacité à résoudre les problèmes pour laquelle elle a été inventée."
G.B. Dantzig, préface de Linear Programming and Extensions
|
|
| " Nous avons aussi [...] pu faire connaître d'une manière assez précise certaines idées sur la théorie des inégalités auxquelles l'illustre géomètre attachait une importance qu'il est permis, aujourd'hui, de trouver un peu exagérée." G. Darboux, préface aux Œuvres de Fourier, t.2.
|  |
|
"Après
ma présentation, le chairman [président de séance] invita à poser des
questions. Il y eut d'abord l'habituel silence de mort; puis une main
se leva. C'était Hotelling. [...]
Il dit: «Mais nous savons tous que le monde est non linéaire!» Ayant
émis cette critique dévastatrice sur mon modèle, il se rassit. Et moi,
virtuellement inconnu, je tâchais frénétiquement de préparer une
réponse convenable.
Tout d'un coup, une autre main se leva. C'était Von Neumann. «Mr Chairman! Mr Chairman! Si le conférencier n'y voit pas d'inconvénient, j'aimerais répondre à sa place.» Évidemment, j'acceptais. Et Von Neumann dit :«Le conférencier a intitulé son exposé 'Programmation Linéaire' et il en a soigneusement posé les axiomes. S'il y a une application qui les satisfait, eh bien, qu'on l'utilise!» "
G.B. Dantzig, préface de Linear Programming and Extension
|
|
La question de l'efficacité, #2: point de vue algorithmique
Le mieux est, là encore, d'abord de rendre la parole à Dantzig:|
"Un exemple simple illustre la difficulté fondamentale.[...] Considérez le problème d'affecter 70 hommes à 70 tâches. Malheureusement, il y a 70! permutations possibles, c'est à dire autant d'affectations. Il faut sélectionner celle qui est optimale pour un certain critère. 70! est un très grand nombre, plus grand que 10100.
Supposez que nous ayons disposé d'un grand ordinateur IBM depuis le Big
Bang, il y a quinze milliards d'années. Aurait-il pu examiner toutes les
possibilités, une par une? Non! Et avec une machine traitant un
milliard d'opérations à la seconde? Toujours non! Et même si la terre
était remplis d'ordinateurs d'une capacité d'une opération par
nanoseconde, travaillant en parallèle, la réponse serait toujours non!
Néanmoins, avec 1040 terres équipées de cette manière, entre le Big Bang et le refroidissement ultime de notre soleil, la réponse serait oui. Ce
qui est remarquable, c'est que la méthode du simplexe, acvec un
ordinateur moderne, peut résoudre le problème en une fraction de
seconde."
|
 |
| " La plupart du temps, cela résolvait un problème à m équations en 2m ou 3m étapes.
C'était vraiment dingue! Je ne m'attendais certainement pas à ce que ce
soit aussi formidable. Je n'avais auparavant rien expérimenté des
problèmes en dimension élevée, et je n'en croyais pas mon intuition
géométrique. Pa r exemple, mon intuition me disait que la procédure exigerait beaucoup trop d'étapes à errer de sommet en sommet adjacent.
En pratique, cela ne prend que quelques étapes. Ce n'est que
maintenant, presque 40 ans après la première exposition de la méthode
du simplexe, que des gens commencent à comprendre un peu pourquoi cela
marche aussi bien." |
|
 |
De fait, assez tardivement (1972), Klee et Minty construisirent un problème à m équations, comportant 2m sommets que l'algorithme du simplexe visitait les uns après les autres: il était ainsi prouvé que l'algorithme ne fonctionnait pas en temps polynomial par rapport aux données: le feeling de Dantzig était loin d'être mauvais! Mais c'était un cas d'école, construit ad hoc, et 30 ans d'expériences... feraient toujours la différence: la quantité de servics rendus sur les cas pratiques défendait brillament, par le nombre de témoignages en sa faveur, l'accusé. En 1984, le mathématicien indien Narendra Karmarkar fit sensation en proposant un algorithme polynomial pour le simplexe: il y eut un grand et légitime émoi chez les théoriciens des algorithmes, mais le succès de l'algorithme de Dantzig, reposant sur sa simplicité et sa robustesse, ne fut pas entamé. |
| ci-contre: N. Karmarkar (source de l'image: IBM, chez qui il travaillaità l'époque de sa découverte ) |
La question de la linéarité (ou non)
Peut-on aller plus loin? Une fonction-objectif non linéaire? Des contraintes non-linéaires? Les deux?Sur un cas aussi "visuel" que notre problème modèle (P), conserver le mêm domaine et considérer un autre type de fonction-objectif n'est pas difficile: il s'agit seulement de changer de type de courbes de niveau. Ainsi, avec:
- z = f(x,y) = x² + y², ce seraient les cercles x² + y² = k ;
- z = f(x,y) = 4 x² + 9 y², ce seraient les ellipses 4 x² + 9 y² = k ;
- z = f(x,y) = x² - y², ce seraient les hyperboles x² - y² = k ;
| Du côté des contraintes... de même qu'on peut fort bien approcher
un cercle par un polygone (n'est-ce pas ce que faisait Archimède pour
calculer son périmètre?), on a tous les jours, sous le nez (à condition
de le lever un peu) des surfaces apporchées par des polyèdres! Le
fameux gherkin de Londres n'est pas la surface lisse que l'on croit, de loin ( portion d'ellipsoïde? de paraboloïde?), mais délimite un domaine convexe qui est un simplexe à beaucoup de facettes (carrées ou triangulaires)! De quoi donner raison... à la fois à Hotelling et à la "correction" apportée par Dantzig: |
détail de facttes planes en verre, dans un centre commercial à Varsovie (Pologne) |
|
"En dernière analyse, bien sûr, Hotelling avait raison. Le monde est
hautement non linéaire. Heureusement, les systèmes d'inégalités
linéaires (contrairement aux égalités) nous permettent d'approcher la
plupart des relations non linéaires rencontrées dans la pratique de la
planification."
G.B. Dantzig, préface de Linear Programming and Extensions
|
Mais... Fourier l'avait dit avant lui, en conclusion du texte de 1824!

Soyons honnête: la conclusion paraît un peu trop optimiste... si la convexité est souvent présente dans les problèmes d'optimisation non linéaires, les techniques en sont tout de même très différentes, et sortent du cadre de cette page. Ceux qui voudraient découvrir le sujet peuvent consulter, en première approche, le petit Que sais-je de Jean-Baptiste Hirriart-Urruty, L'Optimisation (PUF 1996).
Références
Articles
- A. CHAKRABORTY, V. CHANDRU, M.R. RAO, A Linear Programming Primer: from Fourier to Karmakar, Annals of Operation Research (on line;, 2019)
- V. CHANDRU, M.R. RAO, 175 Years of Linear Programming : 1. The French Connection. Resonance, Oct 1998
- H. P. WILLIAMS, Fourier's Method of Linear Programming and its Dual, American Mathematical Monthly, vol. 93, no 9, , p. 681–695
- An Interview with George B. Dantzig, The Father of Linear Programming , College Mathematical Journal, Vol 17, n°4 (Sep 1986)
Quelques Cours en Ligne
- D. ARZELIER, Introcduction à la Programmation Linéaire (INSA de Toulouse)
- F. CLAUTIAUX, Programmation Linéaire (Université de Bordeaux)
- ? DUPUIS, Fondements de la Programmation Linéaire , Méthode du Smplexe (Université Laval, Québec)
- J.-F. SCHEID, Programmation Linéaire (Télécom Nancy)
Livres
- P. CARON, A. JUHEL, F. VANDEVELDE , Programmation Linéaire (Dunod)
- T. CORMEN, C. LEISERSON, R. RIVEST, C. STEIN, Introduction à l'Algorithmique, 2ème édition (Dunod, 2001)
- G.B. DANTZIG, Linear Programming, Theory and Extensions (Princeton 1963)
- G.B. DANTZIG, Linear Programming 1: Introduction (Springer , 1997)
- R. HARTLEY, Linear and non Linear Programming (Ellis Horwood)
- A. KAUFMANN, R. FAURE, Invitation à la Recherche Operationnelle (Dunod)
- B. KOLMAN, R. BECK, Elementary Linear Programming with Applications (Academic Press)
- J. MATOUSEK, B. GÄRTNER, Understanding and Using Linear Programming (Springer)
- M. SAKAROVITCH, Optimisation Combinatoire: Graphes et Programmation Linéaire (Hermann)
- R. SEDGEWICK, Algorithmes en Langage C (Interéditions)
- R. SEDGEWICK, Algorithmes en Java (Pearson)
Poursuivre...
Revenir à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Revenir à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Aller à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Aller à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (Une vie pour Fourier...)
Revenir à la Page Biographique