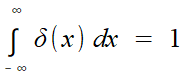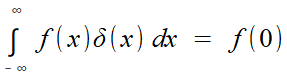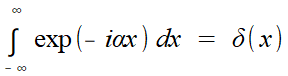La Naissance de la Transformation de Fourier
... Une Promenade Fouriériste! (Partie 3)
De la Série à l'Intégrale
Après avoir rappelé l'équation générale en dimension 3, et la condition initiale, Fourier précise ce qui change, à savoir l'absence de conditions au bord ( "l'état de la surface"... qui délimite le volume, mais l'expression n'est pas très claire, et, pour une fois, il aurait pu meux s'exprimer.). Rappelons aussi que dans ce contexte, le mot intégrale signifie simplement solution.| "Dans les questions que nous
avons traitées précédemment,
l'intégrale
est assujettie à une troisième condition qui
dépend de l'état de la surface. C'est pour cette
raison que l'analyse en est plus composée [...]. La forme
de l'intégrale
est beaucoup plus simple, lorsqu'elle doit seulement satisfaire
à l'état initial; et il serait facile de
déterminer immédiatement le mouvement de la
chaleur selon
les trois dimensions. Mais pour
exposer cette partie de la théorie, et faire bien
connaître suivant quelle loi la diffusion s'opère,
il est
préférable de considérer d'abord le
mouvement
linéaire [...]." Fourier, Théorie Analytique de
la Chaleur,
ch. IX, § 343 ( 1822)
|
Pour plus de clarté, nous avons explicité dans le tableau ci-dessous une comparaison entre le cas borné et le le cas non borné. Toujours dans un souci pédagogique, la fonction arbitraire F de la condition initiale est choisie paire; il traitera ensuite le cas impair, et conclura qu'il suffit de décomposer une donnée initiale quelconque en somme de ses parties paires et impaires, puis d'additionner les deux solutions obtenues. (n°354): l'élégance mathématique du procédé permet aussi de traiter des expressions de taille deux fois moindre!
| segment | domaine | droite (infinie) |  |
| y = u (x, t) | inconnue | y = u (x, t) | |

|
évolution | 
|
|
| u (a, t) = 0 u (b, t) = 0 |
conditions au bord |
néant | |
| u (x, 0) = F(x) | conditions initales | u (x, 0) = F(x) | |
| F arbitraire sur [ a , b ] prolongée par périodicité |
F arbitraire sur [ a , b ] nulle en dehors |
Tout de suite, l'Inversion
Il vient tout à la fois d'écrire F comme transformée de Fourier (cosinus) de Q et de poser le problème de son inversion, c'est à dire trouver une formule qui donne Q en fonction de F. C'est en un
seul paragraphe, le
§346, et moins de deux pages, qu'il va le résoudre,
et
donner la formule d'inversion! Démonstration, suggestion de
preuve, simple analogie, heuristique audacieuse... cela peut se
discuter, et il ne sera pas interdit que tous les lecteurs soient
d'avis divergents, sauf sans doute pour exclure
catégoriquement
la
première option: démonstration. Voici le texte
brut, et
quelques éléments d'appréciation.
Le mot transformation n'apparaît pas encore, mais il l'explicitera plus loin.
Le mot transformation n'apparaît pas encore, mais il l'explicitera plus loin.
 |
 |
|
De F transformée de
Fourier de Q... |
à Q = f(q) transformée de Fourier de F! |
Il est certain que
Fourier veut imiter, en le serrant au plus près, son travail
sur les séries. Avec
son sens de l'esthétique, il a dû
apprécier le résultat
auquel il parvient, et, qui sait, il en
a peut-être, avant tout calcul
deviné la forme, au coefficient près?
Car dans les deux cas, on exprime F par une somme des valeurs de Q cos qx; si dans le premier Q est une somme sur la période des valeurs de F cos qx, pourquoi n'en irait-il pas de même dans le second, à ceci près que l'absence de périodicité peut être vue comme... l'existence d'une période infinie.
Car dans les deux cas, on exprime F par une somme des valeurs de Q cos qx; si dans le premier Q est une somme sur la période des valeurs de F cos qx, pourquoi n'en irait-il pas de même dans le second, à ceci près que l'absence de périodicité peut être vue comme... l'existence d'une période infinie.
| discrète (valeurs
espacées) |
Type de sommation | continue (tous le réels) |
| série | Outil de sommation | intégrale |
| i, présent deux fois: Qi , cos (qi x) | Sommation prise sur | q, présent deux fois: Q (q) , cos (q x) |
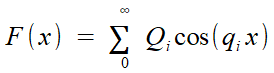 |
condition initiale t = 0 | 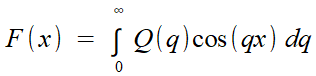 |
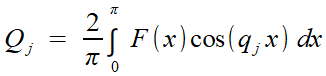 |
calcul
inverse: Q en fonction de F |
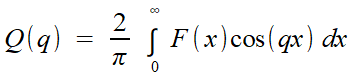
|
Pourquoi,
alors, direz-vous, ne pas se lancer dans le calcul de
l'intégrale de F(x) cos qx? C'est
qu'il est risqué, comme on le verrra un peu plus loin.
Fourier
est eulérien dans son maniement des objets
mathématiques,
mais être eulérien, c'est garder un savant
contrôle
sur les objets manipulés: pas question de jouer
à
l'apprenti sorcier. Il va donc:
Quoi qu'il en soit, ce double subterfuge le ramène à un calcul fait plusieurs fois, l'intégration terme à terme de la série pour évaluer
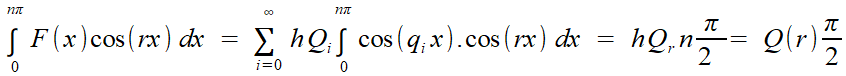
en utilisant l'orthogonalité des cosinus: toutes les intégrales sont nulles, sauf pour un indice j tel que qj = r.
Et c'est bien le problème: ce calcul n'est pas valable pour tout r réel, mais pour une infinité dénombrable. Pas plus que F n'était la série proposée.
Bien sûr, quand n tend vers l'infini, "la série des rectangles devient l'intégrale", et "tout r est un qj" pour notre auteur. On ne sait pas encore que l'ensemble des réels n'est pas dénombrable, et s'approcher n'est pas être égal. C'est toute l'ambiguité de ce raisonnement "par infiniments petits" : l'intégrale est somme d'une infinité de rectangles infinitésimaux, d'épaisseur nulle, mais cette infinité n'est pas dénombrable... Bref, pas moyen d'être convaincu, et il n'est même pas sûr que Fourier le soit à en juger par les retours fréquents sur cette formule dans la suite de son texte.
Quoi qu'il en soit, il tient sa formule de calcul des Q(q) en fonctions des F(x) qu'il n'a plus qu'à reporter dans u (x, t) pour avoir une formule dont on peut aisément vérifier qu'elle est solution de l'équation aux dérivées partielles et de la condition initiale. Autrement dit, même s'il n'a que deviné sans prouver, le physicien Fourier tient la solution correcte du problème de diffusion, tandis qu'il restera au mathématicien Fourier à ruminer sa manière de l'obtenir!

la solution générale (pages 431/432, recomposition)
- d'une part, éviter l'intégration jusqu'à l'infini, en la menant de 0 à nπ. Avec un petit brin d'hypocrisie, en disant aussi que n est infini!
- d'autre part, remplaer l'intégrale donnant F par une série, selon l'approximation classique des rectangles (mais une infinité de rectangles).
Quoi qu'il en soit, ce double subterfuge le ramène à un calcul fait plusieurs fois, l'intégration terme à terme de la série pour évaluer
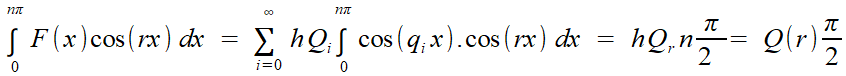
en utilisant l'orthogonalité des cosinus: toutes les intégrales sont nulles, sauf pour un indice j tel que qj = r.
Et c'est bien le problème: ce calcul n'est pas valable pour tout r réel, mais pour une infinité dénombrable. Pas plus que F n'était la série proposée.
Bien sûr, quand n tend vers l'infini, "la série des rectangles devient l'intégrale", et "tout r est un qj" pour notre auteur. On ne sait pas encore que l'ensemble des réels n'est pas dénombrable, et s'approcher n'est pas être égal. C'est toute l'ambiguité de ce raisonnement "par infiniments petits" : l'intégrale est somme d'une infinité de rectangles infinitésimaux, d'épaisseur nulle, mais cette infinité n'est pas dénombrable... Bref, pas moyen d'être convaincu, et il n'est même pas sûr que Fourier le soit à en juger par les retours fréquents sur cette formule dans la suite de son texte.
Quoi qu'il en soit, il tient sa formule de calcul des Q(q) en fonctions des F(x) qu'il n'a plus qu'à reporter dans u (x, t) pour avoir une formule dont on peut aisément vérifier qu'elle est solution de l'équation aux dérivées partielles et de la condition initiale. Autrement dit, même s'il n'a que deviné sans prouver, le physicien Fourier tient la solution correcte du problème de diffusion, tandis qu'il restera au mathématicien Fourier à ruminer sa manière de l'obtenir!

la solution générale (pages 431/432, recomposition)
Revenons un peu sur son
itinéraire: le suivre pas à pas ne nous dit pas
pourquoi il prend ce chemin!
Mais surtout de faire une observation importante sur les intégrales du type F(x) = ∫[0,∞[ f (x,q) dq:
Et pourtant... c'est plus de cent pages en aval qu'il se décide à souligner une des propriétés aujourd'hui classiques: le calcul de la dérivée. Lequel est très facile, puisque la variable ne figure plus que sous un sius ou cosinus. Et là, Fourier oublie toute prudence vis à vis des risques de la dérivation sous l'intégrale, qu'il a lui-même soulevés dès ses premiers exemples!
A-t-il raison? A-t-il tort? Les deux, car si le garde-fou s'impose (comme tout contre-exemple en mathématiques), il est tout aussi important de montrer que l'outil est efficace, et que dans 99% des cas, l'ingénieur en tirera un profit appréciable.
Bizarrement, il ne mentionne pas la propriété "duale" relative à la transformée d'une dérivée, si utile dans l'application aux équations aux dérivées partielles. Il est vrai qu''il peut l'obtenir par transformée inverse! Et puis, il ne veut pas trop "s'écarter du but de l'ouvrage" et tient à nous le redire...Moins anecdotiquement, le procédé est enfin nommé transformation: née 107 pages plus tôt, voilà la transformation de Fourier enfin baptisée!
Sur ce point, comme sur bien d'autres de ce long chapitre IX, on peut
s'interroger: a-t-il été suffisamment
retravaillé
pour la publication? On sait que le manuscrit de 1811 fut
achevé in
extremis
pour la soumission à l'Académie, et cet ultime
chapitre,
comme il n'était pas dans le Mémoire de 1807, a
sans
douté été écrit en dernier
et
peut-être quelque peu souffert du rush final... on
ne peut
exclure qu'il ait été livré "brut du
manuscrit de 1811" pour
l'édition qui marquait la fin d'un combat de 15 ans. Sauf
pour
régler leur compte aux critiques qui lui avaient
été présentées, mais dont
les auteurs
revêtent la tenue de camouflage réglementaire: "On
avait objecté, au sujet de notre analyse... On avait
allégué que, pour résoudre des
questions de ce
genre..."
Consolider par les exemples et des variantes la formule d'inversion donnée au §346 ? Fourier va y revenir au moins deux fois, sans convaincre complètement. Le bref §355 sert de "légitimation morale" du glissement des séries aux intégrales:
Il va maintenant faire directement ce calcul. Dans son premier exemple, il transformait le créneau pair en sinus cardinal (la fonction sc(q)=sin q)/q), il va donc transformer ce dernier, bien décidé à obtenir le créneau, à un facteur multiplicatif près. En deux étapes:
Appliquant ce principe, Fourier se dit qu'il doit pouvoir déduire le cas du prisme infini (pour lequel la solution est une intégrale) de celui de l'armille (pour lequel la solution est une série). Au passage, un petit rappel en forme prise de date! Les termes en sinus et cosinus ont été rassemblés en un seul, par la classique formule d'addition. Pour le passage proprement dit de la série à l'intégrale, pas un mot ne diffère de la variante 1...
Suivons donc la brillante plaidoierie de maître Fourier, dont l'habileté réthorique est bien connue. Sans inquiétude: il n'est pas homme à nous rouler dans la farine, et les idées qu'il présente sont bel et bien celles que l'on met en œuvre dans une preuve d'aujourd'hui.
Arrive alors un point de vue extrêmement moderne (il sera plus tard repris par Gabor dans son perfectionnement de la tranformation de Fourier):
ayant tracé la fonction f (α) (il insiste sur son caractère totalement arbitraire, et il y reviendra à la fin), la fonction p.sc (α -x) = [sin p(α -x)] / (α -x) peut être vue comme une fenêtre qui se déplace, positionnant son maximum face à f (x) et l'essentiel de sa charge (au sens électrique, c'est à dire sa contribution à l'aire) au voisinage de x. Tout se passe donc comme dans le cas particulier étudié précédemment, qui était celui d'une fonction constante f (α)=1. Á ceci près: en face du maximum p de la fenêtre se trouve la valeur f (x), considérée co mme valeur constante de f dans le voisinage infinitésimal de x seul contributeur à l'intégrale. Ce qui permet de la sortir de l'intégrale et de conclure!
On notera avec quelque amusement la remarque finale, qu'on pourrait traduire par: "J'espère que vous n'avez rien contre, car tout le monde fait comme ça en matière de calcul infinitésimal!" Ce qui renvoie au statut de la preuve évoqué au début; ici, Fourier en appelle à une sorte de consensus social du monde savant. D'un autre côté, son insistance a quelque chose de celle de l'étudiant un peu tricheur qui appuie sur les mots parce qu'il sait bien, au fond, que son argumentation n'est pas irréprochable et qu'il est le premier à en douter. Cette balance permet de penser qu'il a une idée clairvoyante de la preuve, tout en admettant en son for intérieur qu'il y manque un peu de rigueur.
De fait, si la démonstration contemporaine s'appuie sur cette idée, sa réalisation "selon la méthode ε, δ de Weierstrass" exige un découpage de l'intégrale et des majorations soignées des contributions respectives d'un voisnage de x et de tout le reste!
| Fourier: archaïque... ou
hyper-futuriste? Et si Fourier
avait tenté
directement l'intégration de 0 à ∞?
Ce n'est pas impossible... mais voici ce qui se serait passé, et qui, peut-être, l'a fait reculer vers la rédaction ci-dessus: 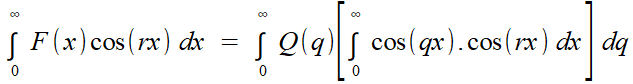 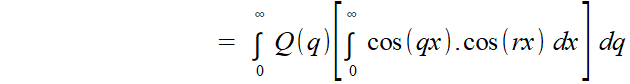 Intervertir les intégrales, soit, personne n'aurait, en ce temps, soulevé d'objection. Mais le crochet est une intégrale ... qui n'a pas de sens! Si Fourier a écrit ces deux lignes, il a dû trouver la chose un peu raide, même s'il n'en est pas tout à fait à la première du genre... Et même: pourrait-il encore invoquer la fameuse orthogonalité des cosinus entre eux, c'est à dire lui attribuer la valeur 0, sauf si r = q, ce qu'il veut faire à tout prix? Or cet argument est capital pour conclure, ici comme dans les chapitres précédents. Double impasse, qui peut justifier les contorsions précédentes, même si elles ne se révèlent pas complètement probantes... Qu'à cela ne tienne: signons un pacte avec le diable, et poursuivons. Le coup de force accompli, il n'est pas plus déraisonnable d'écrire 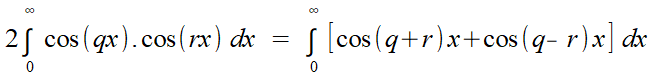 Il suffirait donc
de donner un
sens à une seule intégrale qui n'existe pas,
celle du
cosinus: pactiser avec le diable, soit, mais alors, autant payer le
moindre prix. Imaginons qu'il existe une "fonction" telle que
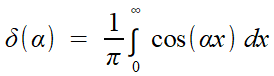 (*) (*)Une "fonction" un
peu
extraordinaire, évidemment... Imaginons! Oui, imaginons,
comme
nous le dit, pour l'éternité, John Lennon depuis
Central
Park
Admettant la
propriété (*) , la fin du
calcul est immédiate!
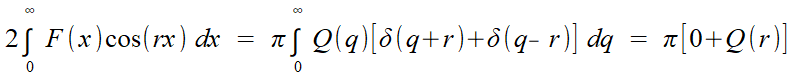 Eh bien, le Mathouriste n'a plus qu'à continuer sa citation de Lennon: "Vous pouvez penser que je suis un rêveur, mais je ne suis pas le seul!" Voyez plutôt cet extrait d'un cours d'Analyse de Fourier très récent (2016), destiné aux étudiants de physique (L3), et téléchargeable ici. L'auteur, Éric Aristidini, est responsable d'un Cours d'Optique Ondulatoire (Université de Nice Sophia-Antipolis), et cela n'a rien fortuit, vue l'importance de la transformation de Fourier en Optique! Cliquez pour agrandir, ce sera
plus confortable!
C'est la même histoire, racontée avec les exponentielles complexes pour plus de concision et de maniabilité, le calcul de TF(1) ayant été légitimé précédemment, dans une présentation de la "fonction de Dirac" très accessible, en version adoucie de distributions, histoire de ne pas trop malmener les étudiants! Avec son "n = 1/dq", Fourier n'est pas si loin que cela de l'approche de la distribution δ comme "limite" d'escaliers d'aire constante 1. En faire un précurseur de Schwartz serait sans doute exagéré, mais il est certain en revanche que, dès ses premiers papiers, Schwartz s'occupe de la fonction de Dirac et de la transformation de Fourier!
|
|||||||||||||
Étudier la Transformation de Fourier?
Fourier donne alors deux exemples (qui vont devenir des classiques de cours!) qui montrent que sa formule d'inversion permet d'obtenir immédiatement les valeurs de certaines intégrales. L'idée est de faire un calcul très simple de transformée (un créneau dans le premier cas, exp(-|x|) dans le second); puis d'appliquer la formule d'inversion, qui lui fournit des résultats beaucoup moins classiques: la transformée du sinus cardinal (sin q)/q dans le premier, celle de 1/(1+q²) dans le second. |
 |
|
en partant du créneau.... |
ou de exp(-|x|) |
Mais surtout de faire une observation importante sur les intégrales du type F(x) = ∫[0,∞[ f (x,q) dq:
- Même avec f très régulière -et en tout cas, continue, F peut être discontinue;
- Même avec f très régulière -et en tout cas, partiellement dérivable en x, F peut ne pas être dérivable.
Et pourtant... c'est plus de cent pages en aval qu'il se décide à souligner une des propriétés aujourd'hui classiques: le calcul de la dérivée. Lequel est très facile, puisque la variable ne figure plus que sous un sius ou cosinus. Et là, Fourier oublie toute prudence vis à vis des risques de la dérivation sous l'intégrale, qu'il a lui-même soulevés dès ses premiers exemples!
A-t-il raison? A-t-il tort? Les deux, car si le garde-fou s'impose (comme tout contre-exemple en mathématiques), il est tout aussi important de montrer que l'outil est efficace, et que dans 99% des cas, l'ingénieur en tirera un profit appréciable.
Bizarrement, il ne mentionne pas la propriété "duale" relative à la transformée d'une dérivée, si utile dans l'application aux équations aux dérivées partielles. Il est vrai qu''il peut l'obtenir par transformée inverse! Et puis, il ne veut pas trop "s'écarter du but de l'ouvrage" et tient à nous le redire...Moins anecdotiquement, le procédé est enfin nommé transformation: née 107 pages plus tôt, voilà la transformation de Fourier enfin baptisée!
 |
|
Des Preuves Alternatives de la Formule d'Inversion?
| Avertissement: autant les Variantes 1 & 2 peuvent être sautées en prmière lecture, autant nous conseillons la troisième au lecteur "non-technicien" des mathématiques: Fourier y suggère admirablement ce qui se passe! Ce serait dommage de vous en priver... |
Consolider par les exemples et des variantes la formule d'inversion donnée au §346 ? Fourier va y revenir au moins deux fois, sans convaincre complètement. Le bref §355 sert de "légitimation morale" du glissement des séries aux intégrales:
| "
[Cette solution] fait connaître distinctement quel rapport il y a
entre les intégrales définies que nous venons d'employer,
et les résultats de
l'analyse que nous avons appliqués aux solides d'une figure
déterminée. Lorsque, dans les séries convergentes
que cette analyse fournit, on donne aux quantités qui
désignent les dimensions, une valeur infinie; chacun
des termes devient infiniment petit, et la somme de la série
n'est autre chose qu'une intégrale. On pourrait passer de la
même manière et sans aucune considération physique
des diverses séries trigonométriques que nous avons
employées dans le chapitre III aux intégrales définies; il nous suffira de donner quelques exemples [...]." Fourier, Théorie Analytique de
la Chaleur,
ch. IX, § 355 ( 1822)
|
Calcul Direct de certaines Transformées Inverses...
Dans sa première étude, Fourier était parti de la formule générale donnant F en fonction de Q, puis avait regardé l'intégrale comme une série "de pas infinitésimal" avant d'exploiter (passage douteux de son esquisse démonstrative) l'orthogonalité des cosinus comme dans le cadre des solides particuliers, pour donner Q en fonction de F.Il va maintenant faire directement ce calcul. Dans son premier exemple, il transformait le créneau pair en sinus cardinal (la fonction sc(q)=sin q)/q), il va donc transformer ce dernier, bien décidé à obtenir le créneau, à un facteur multiplicatif près. En deux étapes:
- Sans en justifier le choix, il prend pour point de départ un développement qu'il a écrit dès le §222 (p.237), grâce auquel il récupère la tranformée de Fourier sinus de sc. Dans le détail, la transition de l'intégrale à la série souffre des mêmes flottements que le calcul général d'inversion: n infini, i=q/dq... Au passage, il obtient la célèbre intégrale (dite, mais plus tard, de Dirichlet) affirmant qu'elle est "connue depuis longtemps"... sans plus de précision!
- Une simple linéarisation de sin q cos qx lui fournit le résultat cherché, et il coïncide bien avec celui obtenu par application de la formule d'inversion. La barre au dessus d'une quantité, x+1 ou x-1 équivaut à une mise entre parenthèse dans le produit par q.
| pages recomposées (afin d'éviter qu'un paragraphe ne soit à cheval sur deux pages). | |
... Ou de toutes les Transformées Inverses? (Variante 1)
|
Après avoir traité dans la même veine le deuxième calcul, et obtenu... Il part de son développement en série trigonométrique et déduira pour elle une formule générale d'inversion (e) dont il n'a plus qu'à souligner qu'elle est le pendant de celle trouvée pour les fonctions paires... Les intégrales des coefficients de Fourier sont prise de 0 à π, mais le changement d'échelle étend l'intervalle de 0 à nπ, qui a vocation à s'étirer jusqu'à l'infini; nous ne disons rien d'autre aujourd'hui lorsque nous regardons le cas d'une fonction non-périodique comme ca limite d'une période qui s'allonge, s'allonge... jusqu'à devenir infinie! Mais là où il n'y a pour nous qu'une heuristique, Fourier croit -ou fait semblant de croire- à la preuve. nπ ou l'infini, ce sera la même chose, le petit ballet entre i, n, dq est rigoureusement le même. Si la preuve diffère par le point source, sa faiblesse est clairement la même. Il a cependant évité ce qui pouvait paraître le plus scabreux, l'intégrale sur [0,∞[ du produit des cosinus... on ne va pas tarder à le retrouver. |
 |
De l'Armille au Prisme Infini (Variante 2)
Qu'est-ce qu'une droite? Un cercle dont le rayon a crû jusqu'à l'infini!Appliquant ce principe, Fourier se dit qu'il doit pouvoir déduire le cas du prisme infini (pour lequel la solution est une intégrale) de celui de l'armille (pour lequel la solution est une série). Au passage, un petit rappel en forme prise de date! Les termes en sinus et cosinus ont été rassemblés en un seul, par la classique formule d'addition. Pour le passage proprement dit de la série à l'intégrale, pas un mot ne diffère de la variante 1...
 |
 |
| pages recomposées (afin d'éviter qu'un paragraphe ne soit à cheval sur deux pages). | |
Une Heuristique Graphique (Variante 3)
Convaincre... d'une autre manière encore, le plus visuellement possible. D'ailleurs, qu'est-ce que démontrer? Le mathématicien démontre un théorème, le procureur démontre la culpabilité du prévenu, l'avocat démontre l'innoncence ..du même, parle-t-on bien de la même chose? Non, bien sûr... mais, Poincaré l'a fort bien dit, démontrer n'est pas comprendre: on peut vérifier le passage rigoureux d'une ligne à une autre, sans pour autant saisir l'esprit de la preuve, que l'on aurait été bien incapable d'imaginer le premier! En revanche, ce que nous appelons souvent prouver avec les mains (l'avocat, lui, ferait un effet de manche...) peut nous faire saisir l'idée qui nous fait défaut; à nous d'être conscients que c'est en dessous des standards de rigueur admis dans la profession, qu'il faudra complèter par du travail, parfois long et prénible.Suivons donc la brillante plaidoierie de maître Fourier, dont l'habileté réthorique est bien connue. Sans inquiétude: il n'est pas homme à nous rouler dans la farine, et les idées qu'il présente sont bel et bien celles que l'on met en œuvre dans une preuve d'aujourd'hui.
|
Ayons d'abord un petit sourire pour le prêchi-prêcha de "l'abbé Fourier" qu'il a bien failli être: pas question de badiner avec le soin, et quant au théorème d'inversion, hors de lui, point de salut, ou peu s'en faut! Pourtant, il n'y va pas de main morte en posant la formule d'inversion qu'il entend justifier. C'est la formule (E) de la page 448 (montrée plus haut), mais...y aviez-vous remarqué le passage en force? Regrouper les sinus et cosinus grâce à la formule d'addition, bien sûr; seulement, il a en même temps interverti l'ordre des intégrations!
L'écriture suivante peut à son tour surprendre: il se sert de la primitive comme s'il avait eu une intégrale sur [0, P], puis assigne à P la valeur infinie. On veut bien le suivre en remplaçant l'intégrale sur [0,∞[ par une intégrale sur [0, P], et ensuite en prendre la limite, mais elle n'existe pas davantage. Le résultat devrait être la "fonction" de Dirac δ(α -x) ! Voyons comment Fourier va tourner autour... sans la nommer, et argumenter pour nous la faire sentir. |
 |
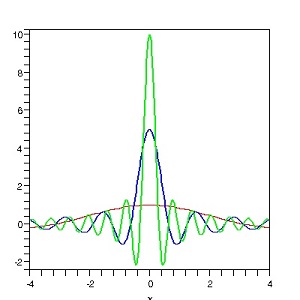
| Fourier commence par étudier la foncrion de t, (sin pt)/t , et ses déformations quand p varie. On l'imaginerait presque, animant son TD à l'École Polytechnique: "tracez la courbe, pour p=1, p=5, p=10, qu'observez-vous?"
S'il avait eu des ordinateurs
et des écrans, gageons qu'il n'aurait
pas hésité à les faire employer!
Les arches se resserrent, mais l'ordonnée en 0, qui vaut p, augmente, pendant que l'aire (l'intégrale) reste invariante. Puisque plus p est grand, plus deux arches successives, positives et négatives, tendent à se compenser ( le 1/x n'a "presque pas" varié), vient l'idée que c'est essentiellement un voisinage de 0 qui contribue à l'intégrale. |
 |
|
 |
 |
|
| ci-contre: (sin px)/x pour: p=1 (rouge), p=5 (bleu), p=10 (vert) |
||
Arrive alors un point de vue extrêmement moderne (il sera plus tard repris par Gabor dans son perfectionnement de la tranformation de Fourier):
ayant tracé la fonction f (α) (il insiste sur son caractère totalement arbitraire, et il y reviendra à la fin), la fonction p.sc (α -x) = [sin p(α -x)] / (α -x) peut être vue comme une fenêtre qui se déplace, positionnant son maximum face à f (x) et l'essentiel de sa charge (au sens électrique, c'est à dire sa contribution à l'aire) au voisinage de x. Tout se passe donc comme dans le cas particulier étudié précédemment, qui était celui d'une fonction constante f (α)=1. Á ceci près: en face du maximum p de la fenêtre se trouve la valeur f (x), considérée co mme valeur constante de f dans le voisinage infinitésimal de x seul contributeur à l'intégrale. Ce qui permet de la sortir de l'intégrale et de conclure!
 |
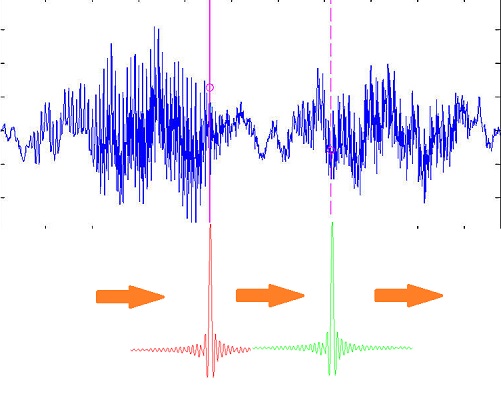 Une f très quelconque: un signal de parole!
Á la position rouge (x à l'abcisse du pic rouge) , le produit rouge-bleu ne "retiendra" du signal bleu que la contribution d'un petit voisinage de la position, puisque
|
|
 |
 |
|
On notera avec quelque amusement la remarque finale, qu'on pourrait traduire par: "J'espère que vous n'avez rien contre, car tout le monde fait comme ça en matière de calcul infinitésimal!" Ce qui renvoie au statut de la preuve évoqué au début; ici, Fourier en appelle à une sorte de consensus social du monde savant. D'un autre côté, son insistance a quelque chose de celle de l'étudiant un peu tricheur qui appuie sur les mots parce qu'il sait bien, au fond, que son argumentation n'est pas irréprochable et qu'il est le premier à en douter. Cette balance permet de penser qu'il a une idée clairvoyante de la preuve, tout en admettant en son for intérieur qu'il y manque un peu de rigueur.
De fait, si la démonstration contemporaine s'appuie sur cette idée, sa réalisation "selon la méthode ε, δ de Weierstrass" exige un découpage de l'intégrale et des majorations soignées des contributions respectives d'un voisnage de x et de tout le reste!
Prouver à la mode d'aujourd'hui!
Outre les ouvrages ci-dessous, les étudiants pourront consulter avec fruit le document Dirichlet, Fourier, Plancherel rédigé à l'intention de candidats à l'agrégation interne par Jean-François Burnol (Université Lille-I) : l'approche de ce théorème y est volontairement très élémentaire, et vous permettra de juger par vous-même de la proximité avec la présentation de Fourier lui-même!Références
-
S. ANNARATONE, Les Premières Démonstration de la Formule Intégrale de Fourier (en ligne sur le site Numdam)
- B. BURKE-HUBBARD, Ondes et Ondelettes (Belin-Pour la Science)
- A. DOMINGUEZ, Highlights in the History of the Fourier Transform (en ligne sur le site de l'IEEE)
- C. GASQUET, P.WITOMSKI, Analyse de Fourier et Applications (Dunod)
- T. KÖRNER, Fourier Analysis (Cambridge University Press)
- E. PRESTINI, The Evolution of Applied Harmonic Analysis: Models of the Real World (Birkhaüser)
Oeuvres de Fourier disponibles en téléchargement sur le site de la B.N.F.
- Théorie Analytique de la Chaleur (édition de 1822)
- Œuvres de Fourier, tome2: Mémoires publiés dans divers recueils (publiés par Gaston Darboux)
Poursuivre...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique