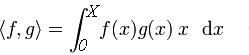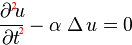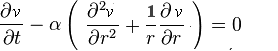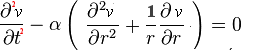L'Armille, la Sphère, le Cylindre et les Autres...
... Une Promenade Fouriériste! (Partie 2)
| "On a traité
jusqu'ici les questions fondamentales
de la chaleur,
et considéré l'action dans les corps principaux.
L'ordre et l'espèce des questions ont
été tellement
choisis, que chacune d'elles présentât une
difficulté nouvelle et d'un degré plus
élevé." Fourier, Théorie Analytique de
la Chaleur,
ch. VIII, § 341 ( 1822)
|
L'Armille
Après deux variables d'espace sans qu'intervienne le temps (la lame), deux variables encore, mais cette fois la variable temps et une seule variable d'espace!
Pourquoi l'armille, et pas la barre rectiligne? Fourier n'en dit rien... Il se peut qu'après un cas avec conditions aux limites, sans condition initiale, il veuille faire l'inverse: étudier un cas avec condition initiale, "sans" conditions aux limites, en raison de la forme de l'anneau... en apparence du moins, car cela conduit à les remplacer par une condition de périodicité, il est vrai assez intuitive.
Ou ne serait-ce pas plutôt une façon plus naturelle d'introduire, avec une condition initiale périodique, un développement en série trigonométrique ?
|
Il pourrait, comme au chapitre III, séparer les variables en cherchant les fonctions u(x,t) = f(x).g(t)
On ferait alors le travail de la même manière,
obtenant
les deux équations différentielles ordinaires g'(t)
= m.g(t) ; f"(x) = - N.
f(x)
et m = -K.N La
périodicité forcerait évidemment
à prendre N
= n².
Fourier ne prend pas cette peine: la périodicité d'une part, la décroissance exponentielle en fonction du temps (à laquelle il s'attend) d'autre part, lui fournissent cette solution évidente, et, il le remarque un peu plus loin, sa "sœur jumelle" en cosinus. Source du document :
BnF
|
|
Fourier dispose donc d'un ensemble de solutions élémentaires suffisamment vaste, les
Source du document : BnF
- le développement de la fonction F donnant la température initiale;
- la vérification par la série formée de toutes les conditions demandées;
- le calcul des coefficients (qui renvoie, bien sûr, aux formules générales des coefficients de Fourier du chapitre III):
- en prime, au début du § 241, l'approximation de la série par ses deux premiers termes, suivi d'une ode glorifiant ce qu'on appellera bientôt les modes propres du problème, qui sont mathématiquement à la chaleur ce que sont les modes propres de vibration à une corde (pour qui l'expression a été inventée):
| "Ainsi les valeurs
particulières que nous avons
considérées précédemment,
et dont nous composons
la solution générale, tirent leur
origine de la question elle-même. Chacune d'elles
représente un
état élémentaire qui peut subsister de
lui-même dès qu'on le suppose formé;
ces valeurs ont une relation
naturelle et nécessaire avec les
propriétés physiques de la chaleur." Fourier, Théorie Analytique de
la Chaleur,
ch. IV, § 241 ( 1822)
|
Il s'offre pour terminer une assez longue digression pour traiter le problème d'une autre manière: considérant d'abord le cas d'un nombre fini de masses réparties régulièrement sur l'armille, il fait tendre ce nombre vers l'infini pour retrouver ses résultats, levant le voile sur son approche:
| "On
pourrait résoudre la question pour un nombre
déterminé de corps, et supposer ensuite ce nombre
infini.
Cette méthode de calcul a
une clarté qui lui est propre, et qui dirige les
premières recherches.
Il est facile ensuite de passer à une méthode
plus
concise dont la marche se trouve naturellement indiquée." Fourier, Théorie Analytique de
la Chaleur,
ch. IV, § 278 ( 1822)
|
Et voici qu'il passe aux aveux: c'est ainsi qu'il a obtenu la série solution, puis, faisant t = 0, le développement de la condition initiale sous une forme comportant des intégrales: ainsi lui sont apparus "pour la première fois" les coefficients de Fourier sous forme intégrale, et la révélation du calcul par orthogonalité !
|
|
|
Source des documents : BnF
|
Enfin, doit-on préciser que la physique expérimentale n'est pas oubliée? Elle était présente dès la mise ne équation, au chapitre II.
|
|
Source des manuscrits : BnF |
| croquis décrivant le
dispositif expérimental de l'armille. |
relevé d'expériences: y compris la date, qui nous renseigne sur l'avancement du travail de Fourier! |
La Sphère
Préparation
Si l'équation de la chaleur demeure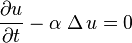
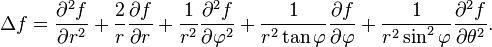
Fort heureusement, le problème que se pose Fourier, à savoir le refroidissement dans l'air ambiant d'une sphère préalablement chauffée, possède d'évidence la symétrie sphérique: le refroidissement s'opère de même dans toutes les directions. La fonction cherchée sera donc radiale, c'est à dire ne dépendra que de la coordonnée sur le rayon, r, et non des deux angles. En ce cas, l'expression du laplacien est déjà moins farouche:
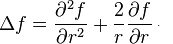
On regarde donc désormais la fonction inconnue v de Fourier comme fonction des seules variables r (espace) et t (temps)
| évolution | 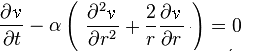 |
coordonnées
sphériques |
| condition au bord |
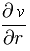 (R, t) + h.v (R, t) = 0 (R, t) + h.v (R, t) = 0 |
échange avec l'air ambiant |
| condition initale | v (r, 0) = F (r) | F donnée |
Nous pouvons donc maintenant lire Fourier, qui commence par énumérer au §283 ces trois conditions:
Mais puisqu'il a retrouvé... la même équation que dans le cas de l'armille, inutile de refaire les calculs: les solutions élémentaires sont les mêmes!
Des Racines et des Modes...
L'intéressant, la nouveauté arrivent en se penchant sur la condition à la limite R (X pour Fourier); puisque c'est une condition de nullité, il suffit de la vérifier sur chaque composante élémentaire pour qu'elle reste vraie pour toute somme, finie ou non. La traduction est immédiate, mais conduit à une équation transcendante, dont les solutions exactes ne peuvent plus être explicitées. Il n'y a de quoi arrêter- ni le "mathématicien pur" Fourier, qui va remplacer la suite d'entiers n = j de l'armillepar une suite de réels n j pour la sphère,ce qui lui fournira encore une famille dénombrable de fonctions comme "base" de développement,
- ni le "mathématicien appliqué" Fourier, qui va nous indiquer comment les évaluer numériquement. Et si nous avons mis ces qualificatifs entre guillemets, c'est pour mieux montrer que cette séparation n'a guère de sens: il n'y a que des mathématiciens... ou alors, ce ne sont pas de vrais mathématiciens!
|
|
|
| Étude de
l'équation, ramenée à tan ε = ε
/ λ
Selon
la pente, la droite coupe, ou ne coupe pas, le premier arc ailleurs
qu'en la solution triviale 0; en prolongeant (mentalement) la figure
vers le haut, on imagine facilement l'existence d'une racine unique
dans chaque intervalle délimité par les
asymptotes
verticales.Source des documents : BnF
|
Fourier présente le calcul par approximations successives, ayant disposé convenablement l'itération pour assurer la convergence.; il détaille l'interprétation graphique, en soulignant qu'il est possible de partir d'une valeur supérieure comme d'une valeur inférieure à la racine cherchée, voire coupler les deux pour obtenir un encadrement.
| |
|
| Étude de
l'itération, présentée avec le graphe
de la fonction tan
sous la forme tan εn+1
= εn / λ
mais en fait
réalisée numériquement sous la formeεn+1
= arc tan εn
/ λ
Source des documents : BnF
|
Et tout ceci pour conclure qu'au fond, cette digression n'avait rien d'indispensable. Pourtant, si les mémoires de 1807 et 1811 ont éventuellement la marque d'un écrit terminé en hâte, ce ne peut être le cas ici: Fourier a eu le temps et le sésir de peaufiner le texte édité. Alors, c'est peut-être une réponse indirecte aux critiques de ses pairs, Lagrange, Laplace, Poisson...
| "Au reste la
solution que nous avons donnée n'est point fondée
sur la
propriété d'avoir toutes ses racines
réelles. Il n'aurait donc pas été
nécessaire
de démontrer cette proposition par les principes de
l'analyse algébrique. Il suffit pour l'exactitude de la
solution
que l'intégrale puisse coïncider avec un
état
initial quelconque [...]" Fourier, Théorie Analytique de
la Chaleur,
ch. V, § 305 ( 1822)
|
Un Développement d'un Nouveau Genre
La suite parait d'abord tenir de la routine: former une série candidate, avec des coefficients non précisés; puis ajuster ces derniers au bord, pour t = 0.Ce que Fourier vient de réaliser, c'est l'un des premiers développement en série de fonctions orthogonales. Certes, comme souvent en sciences, l'idée est dans l'air du temps: dans son étude du potentiel de l'ellipsoïde, en 1785, Legendre a obtenu des relations d'orthogonalité entre "ses" polynômes. Mais il n'a pas développé une fonction quelconque! L'article de Gauss sur les quadratures approchées, considéré comme séminal pour la notion de polynômes orthogonaux, date, lui, de 1814 -il est donc postérieur aux deux premiers mémoires de Fourier; et le concept d'orthogonalité ne sera pleinement dégagé qu'en 1826 par Jacobi, dans le sillage de Gauss.
Avec tout le confort des notations modernes, et l'abus de vocabulaire, commun chez les physiciens, mais qui fait ticquer les mathématiciens (le mot exact serait base hilbertienne, mais il est un peu plus difficile à définir!), le travail effectué se résume, de façon aussi esthétique que compacte, en:
| "base" | φj (x) = sin nj x / x | fonctions propres |
| produit scalaire | 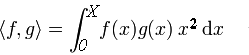 |
"poids" x² |
| orthogonalité | < φi , φj > = 0 | i et j distincts |
| coefficients | aj = < F , φj > / < φj , φj > |
Voilà qui est promis à une belle descendance mathématique, et Fourier va être, dès le chapitre suivant, encore le premier à explorer la voie qu'il vient d'ouvrir. Mais avec toutes ces belles mathématiques, il ne faudrait pas oublier la physique. D'abord, rappeler que, comme pour la lame, comme pour l'armille, les séries théoriques laissent la place, en pratique, à des sommes de quelques termes seulement:
| "Les racines n1, n2, n3, n4, etc. de l'équation
nX / tan nX = 1 - hX sont très
inégales;
d'où l'on conclut que si la valeur du temps
écoulé
t est considérable, chaque terme de la valeur de v est extrêmement petit par
rapport à celui qui le précède.
À mesure que le temps du refroidissement augmente, les
dernières parties de la valeur de v cessent d'avoir aucune
influence sensible; et ces
états partiels et élémentaires qui
composent
d'abord le mouvement général, afin qu'il puisse
comprendre l'état initial, disparaissent presque
entièrement, excepté un seul." Fourier, Théorie Analytique de
la Chaleur,
ch. V, § 292 ( 1822)
|
Bref, tout ceci reste aussi maniable. Puis, viennent les applications physiques proprement dites: un long développement sur les thermomètres, et une annonce spectaculaire:
| "La question du mouvement de la
chaleur dans une sphère comprend
celle des températures terrestres.
Pour traiter cette dernière question avec plus
d'étendue,
nous en avons fait l'objet d'un chapitre séparé."
Fourier, Théorie Analytique de
la Chaleur,
ch. V, § 304 ( 1822)
|
En outre, la chaleur dans une sphère, cela peut concerner aussi une serre, témoins ces géantes (dédiées à la présentation d'un nombre ahurissant d'espèces) inspirées par les célèbres dômes géodésiques de Buckminster Fuller!
.
Extérieur et intérieur des serres de l'Eden Project, St Austell (Cornouailles, Grande Bretagne)
Le Cylindre
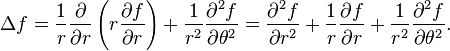
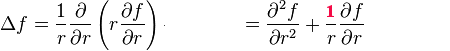
X=R est maintenant le rayon du cylindre, et sans surprise la condition au bord s'y traduit de la même manière. À nouveau, le problème n'a plus que deux variable, r qui désigne la position sur le rayon à l'intérieur du cylindre (espace) et t (temps); la fonction inconnue v de Fourier s'écrit
| évolution | 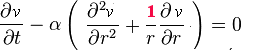 |
coordonnées
cylindriques |
| condition au bord |
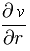 (R, t) + h.v (R, t) = 0 (R, t) + h.v (R, t) = 0 |
échange avec l'air ambiant |
| condition initale | v (r, 0) = F (r) | F donnée |
Aussi Fourier, qui a fait sa mise en équation au chapitre II, écrit-il d'emblée les deux premières, équation de diffusion de la chaleur et condition au bord.
| sphère | r u"(r) + 2.u'(r) + gr u(r) = 0 |
| cylindre | r u"(r) + 1.u'(r) + gr u(r) = 0 |
Oui, mais voilà: finie la petite astuce qui vous ramène aux coefficients constants! On n'est pas dans un exercice de mathématiques où tout a été prévu pour que le calcul s'arrange... Dame nature est moins gentille avec le physicien/mathématicien. Qu'à cela ne tienne, Fourier a de la maîtrise technique -on l'a déjà vu: il cherche les solutions développables en série entière
Et sur quoi peut-il tomber, de cette manière?
Prenons un instant g = 1, pour ne pas nous encombrer: on reconnait l'équation différentielle de Bessel, et le développement en série entère correspondant de la fonction J0! Et ceci, deux décennies avant les écrits (1830) de Bessel (ou biographie en allemand bien plus complète!) dans lesquelles il introduit les célèbres fonctions qui portent désormais son nom, mais que, comme l'a fait unltérieurement remarquer Heine en 1868, on devrait plus justement nommer fonctions de Fourier-Bessel. D'ailleurs, ce dernier n'avait pas pris ombrage de cette antériorité, exprimant au contraire toute son admiration pour son devancier, si l'on en croit Kelvin -lui même, il est vrai, grand admirateur de Fourier.
Timbre allemand pour le bicentenaire de Bessel.
Derrière lui, ses deux premières fonctions, J0 et J1
L'examen attentif se fait à grands coups d'alternance de zéros, à la façon des futurs théorèmes de Sturm. Fourier y est pour le moins allusif, invoque "des propositions fondées sur la théorie des équations algébriques et démontrées depuis longtemps", mais parait bel et bien traiter les séries entières comme s'il s'agissait de simples polynômes. Il y a certainement des lacunes, mais le résultat est le bon. Le joli timbre ci-dessus illustre fort bien ce genre d'entrelacement.
Il reste à traiter la condition initiale, mais auparavant Fourier explore plus avant la fonction de Bessel, parvenant de deux manières à son expression intégrale!
| Utilisation de l'orthogonalité pour le calcul des coefficients, § 318 & 319 (extraits) (Source: BnF) |
|
Petite Digression sur les OndesCertes, dans son livre, Fourier
traite d'un sujet unique: la chaleur. Ce qui ne l'empêche pas de
remarquer, ici ou là, que sa méthode s'applique à
d'autres problèmes. Quoiqu'il ne l'ait pas fait lui-même,
il est intéressant de comparer, pour une propagation/diffusion
radiale, les deux équations des ondes et de la chaleur: bien peu
de choses changent si nous nous attachons à la forme de ces
équations; la constante α
n'est bien sûr pas la même dans les deux cas, mais si cela
est d'une grande importance physique (homogénéité
dimensionnelle), cela n'importe en rien pour le mathématicien,
toujours tenté de pousser la désinvolture jusqu'à
prendre α = 1 !
v (r, t) = j(r). w(t)
la fonction f vérifiera la même équation différentielle, c'est à dire celle de Bessel. g
vérifiera, elle, une équation à coefficients
constants du second ordre, et non plus du premier. C'est tout!On peut donc voir des fonctions de Bessel dans un bassin où se propagent des ondes radiales: vous en rêviez, le Mathouriste l'a fait! (On peut supposer que la condition au bord est d'annuler la solution, ce qui correspond à l'immobilisation sans réflexion de l'onde; cela paraît une approximation acceptable... et fait intervenir sans détour les racines de J0) Leur ressemblance avec des sinusoïdes amorties a d'intéressantes conséquences musicales; nous y reviendrons ailleurs. |
Les Autres...
Références
- Jean-Pierre Kahane, Le Retour de Fourier (Académie des Sciences, 2005) : article à télécharger en cliquant!
- Jean-Pierre Kahane, Le Retour de Fourier Conférence (2006) en VIDEO de l'IREM Paris VII.
- Jean-Pierre Kahane, Coup d'œil sur l'Analyse de Fourier (Mai 2011, École Polytechnique): texte de la conférence.
Jean-Pierre Kahane: une vie au service de l'Analyse de Fourier! (Mai 2011, École Polytechnique )
On reconnait au tableau l'évocation de la naissance de la toute première série écrite par Fourier
dans le Mémoire déposé à l'automne 1811 à l'Académie des Sciences, qui obtiendra le Grand Prix 1812.
Dire qu'il y a des centaines d'ouvrages consacrés à l'Analyse de Fourier n'est sans doute en rien exagéré. Le Mathouriste se limitera, au moins pour l'instant, au choix amoureux de quelques ouvrages qui l'ont particulièrement séduit, et qu'il a classés par ordre d'accessibilité mathématique :
- B. BURKE-HUBBARD, Ondes et Ondelettes (Belin-Pour la Science)
- G. TOLSTOV, Fourier Series (Dover)
- H.POINCARÉ,Théorie Analytique de la Propagation de la Chaleur (G. Carré, 1895 -disponible en ligne sur Gallica-BnF)
- H. LEBESGUE, Leçons sur les Séries Trigonométriques (Gauthier-Villars 1906 -disponible en ligne sur Gallica-BnF)
- C. GASQUET, P.WITOMSKI, Analyse de Fourier et Applications (Dunod)
- E. PRESTINI, The Evolution of Applied Harmonic Analysis: Models of the Real World (Birkhaüser)
- T. KÖRNER, Fourier Analysis (Cambridge University Press)
- J.-P. KAHANE, P.-G. LEMARIÉ, Séries de Fourier et Ondelettes (Cassini)
-
Une analyse du chap. III, sections I & II, p. 159-177. de la Théorie analytique de la chaleur (1822)
-
dans la page consacrée au problème de Sturm-Liouville, une présentation élémentaire de la méthode de Fourier, celle qu'il inaugure avec succès dans la Théorie Analytique: on y étudie trois exemples issus du Mémoire, en progressant du cas le plus simple au plus élaboré, respectant ainsi le modèle de démarche de son ouvrage. Le développement d'une fonction en série de fonctions orthogonales est en effet une généralisation de celui de Fourier -incontournable dans la Physique contemporaine, et l'une des preuves de l'extraordinaire fécondité de son travail.
Oeuvres de Fourier disponibles en téléchargement sur le site de la B.N.F.
- Théorie Analytique de la Chaleur (édition de 1822)
- Œuvres de Fourier, tome2: Mémoires publiés dans divers recueils (publiés par Gaston Darboux)
- Eloge funèbre de Delambre in Tables Astronomiques manuelles de Ptolémée et de Théon
Et aussi...
- Joseph Fourier et la préhistoire de l’effet de serre : une conférence de Raymond Pierrehumbert (univ. de Chicago), en vidéo, sur le site Diffusion des Savoirs de l'École Normale Supérieure.
- La théorie de la chaleur de Fourier appliquée à la température de la Terre: article de James Lequeux sur le site BibNum
Revenir à la Page: Analyse Harmonique... mais pourquoi ce nom? (Prélude à la Théorie Analytique, #0.1)
Revenir à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Aller à la Page: Naissance de la Transformée de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique