Fourier, une Incursion en Théorie des Nombres...
Manuscrit
MS2044, Bibliothèque de l'Institut de France, Paris
(La pagination 311 résulte d'un assemblage qui ne respecte pas la chronologie des cours.) |
Elle est là, dans le cours de Fourier à la première promotion de l'École Polytechnique (An IV: 1795-96), cette preuve de l'irrationalité de la base e des logarithmes népériens, dont on croyait qu'il n'existait aucune trace écrite. Un cours dont la première leçon se tient le 4 Nivôse, c'est à dire... le 25 Décembre 1795: voilà certes un Noël d'exception! Et elle est d'autant plus intéressante que nous en avions, à travers sa version simplifiée, colportée par la tradition, perdu la saveur originale. Jusqu'alors, les preuves d'irrationalité reposaient sur l'usage des fractions continuées, une méthode introduite par Euler, qui l'avait appliquée avec brio au nombre e. Et voilà, pensions nous encore il y a peu, que Fourier, par une illumination aussi géniale que soudaine, avait mis au rancart ces encombrantes étagères de nombres et substitué l'emploi de séries, plus simples, plus intuitives... Mais d'où venait son inspiration? Comment avait-il eu l'idée de cette rupture méthodologique? Ce que nous apprend la lecture de ce cours, c'est que, loin de renier Euler, il l'a adapté. Son innovation fait apparaître le chaînon manquant entre les deux preuves connues, dissipe le mystère de la transition; elle est de surcroît un complément élégant dans la fascinante histoire de l'irrationalité. |
|
|
Ce petit travail
d'investigation nous a été suggéré par
Jean-Pierre Kahane
qui, de conférence en conférence, suggérait
inlassablement qu'il serait bon que le CNRS s'occupât de dépouiller les
archives liées à Fourier... ou, ajoutait-il parfois, quelqu'un qui ait
le temps.
Prenez une minute pour le voir
et l'écouter, vous serez saisi par la pertinence de ses propos: il vous
suffit pour cela de cliquer sur l'image ci-contre.
|
 extrait ( 1'10") de sa conférence (Grenoble, 2016): Quelques Aspects du Retour de Fourier |
|
"Les œuvres de Fourier n'ont jamais été
complètement publiées. Il y a des œuvres, mais il
n'y a pas d'œuvres complètes. Il y a des manuscrits de Fourier,
on les a recensés, mais presque
personne ne les a lus. [...] alors que les manuscrits sont là, on
les voit! Et en les voyant, on apprend des choses."
Jean-Pierre Kahane, Quelques Aspects du Retour de Fourier
|
Le manuscrit auquel nous nous intéressons particulièrement n'est, hélas, pas de la main de Fourier... mais d'un polytechnicien de l'An IV que nous n'avons pas réussi à identifier, en dépit de la consultation des écritures de près de la moitié des presque 400 élèves de cette promotion exceptionnelle. L'École a conservé, dans ses remarquables archives, une trace de chacun de ceux qui ont dû faire une demande à leur hiérarchie, ou présenter un justificatif d'excuses, souvent par un petit billet relatif à un banal problème matériel (cherté de la vie à Paris -déjà!, difficulté à se loger, pour les malheureux provinciaux...)
Afin de bien comprendre l'histoire dans sa continuité, il est nécessaire d'opérer un double flash-back, d'abord sur ce qu'on nommait couramment "preuve de Fourier", puis plus haut dans le temps sur la solution d'Euler.
Ce que nous en savions auparavant...
Nous le savions par le recueil d'exercices publié en
1815 par Janot de Stainville, élève à l'École
(promotion 1802), puis répétiteur dès 1810.  |
 |
 |
| page de titre |
annonce du résultat |
source de la preuve: Fourier! |
| Accès au recueil complet (Google Books) |
||
Deux choses sautent aux yeux; tout d'abord, aucune fraction, seulement le recours à la série, avec un encadrement classique (que Stainville prouve en majorant le reste par une série géométrique de raison 1/(n+1) -procédé classique- ou plus élémentairement avec des intégrations par parties répétées (niveau Terminale S, voir notre page):
La preuve "moderne", dite de Fourier,
en 3 lignes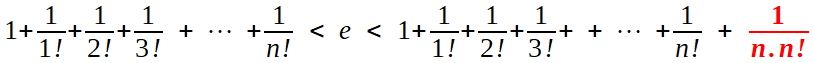 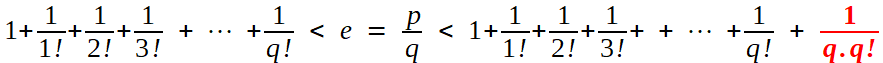 On chasse alors tous les dénominateurs en multipliant par q! ; à gauche figure un entier Nq tel que l'on a 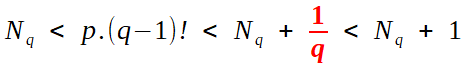 ce qui place l'entier p.(q-1)! entre deux entiers consécutifs, strictement: c'est impossible, et cette contradiction établit l'irrationalité désirée. |
Ensuite, il y a la petite note additionnelle:
|
"Cette démonstration m'a été
communiquée par M. Poinsot, qui m'a
dit la tenir de M. Fourier."
|
Or, il y a une excellente raison pour que Louis Poinsot "la tienne de Fourier": il était de cette première promotion de l'X! Il a donc assisté au cours d'Analyse de Fourier...
Précisons enfin que dans son analyse du texte de Stainville, Norbert Verdier indiquait, après consultation d'un spécialiste ayant recensé et catalogué les œuvres de Fourier qu'il n'existait probablement pas de trace écrite de ce résultat... de fait, ni publication, ni manuscrit de sa main, mais le manuscrit d'un élève -et même, on le découvrira plus loin, de plusieurs- peut faire foi.
Euler, le Grand Prédécesseur
Le développement d'une fraction repose (p.109) sur l'itération de l'algorithme d'Euclide
B = C b + D
C = D c + E
....
|
"Si la fraction court jusqu'à l'infini, A ne sera pas à B comme un nombre, mais irrationnel ou transcendant." L. EULER, De Fractionibus continuis Dissertatio |
Voilà donc un critère qui a le mérite de fonctionner à vue!
Pour l'appliquer à e, Euler part d'une valeur numérique approchée très précise (13 décimales), qui, convertie en fraction (dénominateur 1013), va lui permettre d' observer des progressions arithmétiques dans les quotients partiels successifs, de quoi conjecturer qu'il en va de même, à l'infini, pour le nombre exact. Qui a dit que les mathématiques ne sont pas une science expérimentale?
Si vous voulez en savoir plus sur son travail, y compris la démonstration, nous l'avons détaillé dans cette page; et si en outre vous en avez besoin, vous trouverez aussi une initiation douce aux fractions continues.
Que faisait donc Fourier?
La leçon d'Analyse du 4 Ventôse, An IV (23/02/1796) est consacrée au logarithme et à l'exponentielle; elle commence par la mise en correspondance d'une progression arithmétique (en abcisses) et d'une progression géométrique (en ordonnées), avec le tracé de la "logarithmique" -en fait, le graphe de la fonction exponentielle. Elle va se terminer sur la preuve d'irrationalité de e, qui ne prend même pas une page! Le développement en série de ex a été prouvé deux leçons auparavant.  |
 |
|
| Manuscrit MS2044, Institut de France début de la leçon |
id., fin. le trait rouge correspond à la preuve. |
|
 |
||
Le résultat est annoncé clairement, mais sans tambour ni trompette : pas de commune mesure avec 1 signifie qu'on ne peut trouver deux entiers p et q tels que q.e = p.1; en effet, comme la suite de la démonstration l'indique par un croquis, e-2 et 1 seront regardées comme deux segments dont ce sont les longueurs respectives; on est dans la tradition d'Euclide. Fourier va d'abord présenter la méthode de façon générale:

Sa méthode ressemble à celle au développement en fraction continuée (il parle d'ailleurs de méthode du plus grand commun diviseur); au lieu de mesurer r = RR' sur l'unité, comme cela paraîtrait naturel, il préfère "mesurer 1 avec r" , supposé inférieure à l'unité, c'est à dire compter combien de fois il y a r dans 1. Approcher r ou 1/r, cela importe peu pour évaluer la rationalité; en revanche sa méthode diffère sur deux points:
- d'abord, retenir comme "quotient", non le plancher de 1/r (la partie entière), mais le plafond
(l'entier immédiatement supérieur), avant de définir comme reste
l'excès par rapport à 1 (de manière à avoir une quantité positive)
| ( q- 1) r < 1 ≤ q r ; et soit r' = q r - 1 |
- et surtout, dans la réitération qui va suivre, ne pas mesurer, avec le nouveau reste, le précédent, mais revenir à la comparaison avec l'unité.
Autrement dit, le glissement de reste vers diviseur, caractéristique de
l'algorithme d'Euclide, cède la place à la mesure de l'unité par les
restes successifs; un élément (l'unité) reste immuable tandis que
l'autre évolue au fil de l'itération.
 |
On construit ainsi deux suites qn et Rn telles que:
( q1- 1) R < 1 ≤ q1 R ; 1 = q1 R - R1 ( q2- 1) R1 < 1 ≤ q2 R1 ; 1 = q2 R1 - R2 ......... ( qn- 1) Rn-1 < 1 ≤ qn Rn-1 ; 1 = qn Rn-1 - Rn ......... |
Un point crucial est que cet algorithme fonctionne exactement comme celui des fractions continues, c'est à dire que l'on peut montrer (voir par ex. l'ouvrage de Daniel Duverney cité en référence):
si l'algorithme ne se termine pas, R est irrationnel.
Face à cette itération, Fourier dispose en parallèle le calcul de chaque reste en fonction du suivant.

Extrait du manuscrit MS 668 (Éc. des Ponts & Chaussées)
Il s'agit, à l'évidence, d'une remise au propre (lignes tirées, calligraphie) des notes d'un autre étudiant, également anonyme.
ce qui, de manière générale, s'écrirait
Il "emboîte" successivement les formules de la deuxième colonne (à la façon d'un schéma de Horner) pour obtenir une expression en série du R initial

C'est alors qu'il "inverse le processus", en quelque sorte, en considérant le nombre tel que pour tout n, qn = n , et dont il est évident, en effectuant, qu'il s'agit de e - 2

Le développement est, par construction, infini, donc ce nombre est irrationnel, CQFD.
Fourier n'a même pas écrit ce qui serait l'encadrement de définition du quotient suivant

Ce dernier ne revendiquant rien d'original de sa part, on peut supposer que la simplification de la présentation a été opérée par Poinsot lui-même, à moins que Fourier n'ait "amélioré" son cours à une promotion ultérieure -hélas, nous n'en avons actuellement aucun exemplaire.

Les Manuscrits-sources (Notes d'élèves)
Ils sont au nombre de 4, présentés ci-dessous, et sur
ce point, sont très similaires... pour ce qui est des calculs, mais
plus variés dans le commentaire! "Nous allons lui reconnaître une propriété bien singulière et bien remarquable", annonce MS 1852 avant de la citer de la même façon que MS2044. "une propriété très curieuse", note pour sa part MS 668.
Le seul dont on connaisse l'auteur: Charles Donop, un chef de brigade,
provient des archives personnelles de Vitto Volterra (MS Vitt. Em.
1509, conservé à Rome); il a été étudié et dactylographié (Anne-Marie
Lorrain, Giuseppe Pepe). Ce serait donc a priori celui où l'on aurait
pu repérer bien plus tôt cette preuve, sauf qu'après avoir, sans autre forme d'annonce, souligné que le procédé présente "une analogie frappante avec le résultat de la méthode du plus grand commun diviseur", il parvient à l'expression de e, sans conclure quoi que ce soit sur sa nature arithmétique...
et passe à autre chose. Y a-t-il eu un feuillet perdu? Mystère...
Toujours est-il que dans leur table des matières, les auteurs notent
sobrement "le développement en série de e et son analogie analogie avec la méthode du plus grand commun diviseur" comme si ce développement était le seul but: ahurissant! 
|
 |
 |  |
| Manuscrit
MS 2044 (Bibliothèque de l'Institut de France) |
MS 1852 (Éc. des Ponts & Chaussées) | MS 668 (Éc. des Ponts & Chaussées) |
Manuscrit
MS Vitt. Em. 1509
(Archives de Vito Volterra) |
Seul de tous, MS 1852 évoque explicitement le développement en fraction continuée "classique" et le critère d'irrationnalité associé, à la manière d'Euler.

Remarques finales
1. Fourier n'évoque pas (fût-ce sans démonstration) le résultat de Lambert relatif à π
,
ce qui est relativement surprenant: la démonstration, relativement
compliquée, aurait opportunément été omise, mais on aurait pu attendre
une citation du résultat, s'agissant d'une "propriété bien remarquable"
d'un nombre qui ne l'est pas moins, et qui est la constante
mathématique la plus célèbre. Fourier connaissait-il ce résultat, qui a
son âge à un an près? 2. Ce n'est pas la dernière preuve d'irrationalité de e: Lambert y appliquera sa méthode (plus puissante, elle prouvera qu'il en en va de même pour toutes ses puissances entières); et surtout Hermite y reviendra alors même qu'il en a prouvé la transcendance, au nom d'une véritable profession de foi
|
"On reconnaîtra volontiers que, dans le domaine mathématique, la possession d'une vérité importante ne devient complète et définitive qu'autant qu'on a réussi à l'établir par plus d'une méthode." C. HERMITE, Sur l'Irrationalité de la Base des Logarithmes Hyperboliques |
Pour cette suite de l'histoire, comme sur les détails de l'épisode précédent (le travail d'Euler), on se reportera à
- notre page Irrationalité de e, avec les moyens de Terminale
- et aussi, plus généralement,à la page Promenade dans l'Irrationnel.
- et enfin, en cas de besoin, on trouvera une initiation douce aux fractions continues.
Références
Il s'agit uniquement de références relatives aux techniques employées et à leur place de l'histoire de l'irrationalité, la (vraie!) contribution de Fourier présentér ici n'ayant pas été aperçue avant la fouille de votre serviteur...- H. BOUALEM, R. BROUZET, La Planète R (Dunod)
- D. DUVERNEY, Théorie des Nombres (Dunod)
- L. EULER, les Archives EULER: tout Euler en ligne!
- E. HAIRER, G. WANNER, Analysis by its History (Springer)
- J. HAVIL, The
IrratiΦnals (Princeton University Press)
- E. MAOR, e - The Story of a Number (Princeton University Press)
- M. SERFATI, Quadrature du Cercle, Fractions Continues et Autres Contes (Brochure APMEP n°85)
- J. de STAINVILLE, Mélanges d'Analyse Algébrique & de Géométrie (sur Google Books)
- J. de STAINVILLE, id., extrait sur la "preuve de Fourier", commenté par N. Verdier (sur BibNum)
A.Juhel: Irrationalité et Transcendance: État des Lieux avant Hermite , conférence aux journées Padé (Lycée Faidherbe, Lille, 1994).
- Le Mémoire de Lambert sur l’irrationalité de π (1761) sur BibNum (présenté et commenté par A. Juhel)
- Irrationalité de e, avec les moyens de Terminale (une autre page de ce site)
Poursuivre dans le Monde de Fourier...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique





