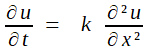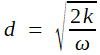Fourier et la Chaleur de la Terre ...
... Some like it Hot!
Un Problème plus actuel que jamais...
Le Mathouriste
n'est parfois qu'un touriste... sans mathématiques -au moins le
croit-il (avant qu'elles ne le rattrapent de façon imprévue, comme ici...). Voici
deux lieux qu'il a aimé découvrir
Mais... quel rapport avec ce que nous présentons ici, autour de Fourier? Il est, hélas, d'une inquiétante actualité; de plus en plus, les climatologues s'alarment de la fonte des glaces au Groenland. Au delà du risque d'altération d'un magnifique paysage glaciaire, cela pourrait occasionner une montée du niveau des océans qu'ils évaluent entre 5m et 7m; de quoi engloutir totalement l'île de Sein, ... un romancier, au cœur de qui la Bretagne est si chère saura, si nos images ne vous l'ont pas assez suggéré, vous convaincre de la vulnérabilté de l'île:
Risquer engloutir Sein, et pas qu'elle! Molène, Groix, Belle-Ile, Oléron... à qui viendrait le tour? L'équilibre thermique de la Terre est donc fragile, très fragile; dans les travaux présentés ici, Fourier est le premier à évoquer l'effet de serre atmosphérique, l'influence de l'activité humaine... et l'âge de la planète bleue. Tout cela à partir de l'équation de la chaleur!
| |
|||
| arriver à l'île de Sein... | ... et la voir du haut de son phare: quelques petits mètres au dessus de l'océan... |
||
Mais... quel rapport avec ce que nous présentons ici, autour de Fourier? Il est, hélas, d'une inquiétante actualité; de plus en plus, les climatologues s'alarment de la fonte des glaces au Groenland. Au delà du risque d'altération d'un magnifique paysage glaciaire, cela pourrait occasionner une montée du niveau des océans qu'ils évaluent entre 5m et 7m; de quoi engloutir totalement l'île de Sein, ... un romancier, au cœur de qui la Bretagne est si chère saura, si nos images ne vous l'ont pas assez suggéré, vous convaincre de la vulnérabilté de l'île:
Risquer engloutir Sein, et pas qu'elle! Molène, Groix, Belle-Ile, Oléron... à qui viendrait le tour? L'équilibre thermique de la Terre est donc fragile, très fragile; dans les travaux présentés ici, Fourier est le premier à évoquer l'effet de serre atmosphérique, l'influence de l'activité humaine... et l'âge de la planète bleue. Tout cela à partir de l'équation de la chaleur!
... et un pionnier de la question: Fourier!
Fourier a écrit deux articles sur la Température du Globe, le premier en 1820, alors que son mémoire sur la chaleur, primé par l'Académie en 1811, n'a toujours pas été publié -inexplicable entorse à l'usage de cette institution- et le second en 1827, après la publication de la Théorie Analytique de la Chaleur (1822). Vu de haut, leur objet est similaire, et l'on pourrait sourire un peu trop facilement:| «Tiens! Dans ce domaine là-aussi, c'était un précurseur, et les chercheurs du XXIème siècle n'ont rien inventé: republier un corps sensiblement analogue sous des habits neufs n'est pas une mode si récente...» |
Mieux vaudra s'interroger sur les raisons sociales de cette course au volume: aujourd'hui, une fâcheuse tendance à juger plus à la quantité qu'à la qualité (ô mannes de Gauss, Pauca sed Matura n'est plus guère de mise), qui contraint à publier à un ryhtme effréné, et pour Fourier la recherche obstinée d'une large reconnaissance qui, en 1820, lui échappe toujours: toute occasion de faire entendre et lire sa théorie doit être saisie. En 1827, il s'agit plus d'une note de synthèse pour ses pairs physiciens, autant que le regard apaisé du savant qui embrasse l'ensemble de son œuvre à l'automne de sa vie. Les dates fournissent donc un contexte complètement différent à ces deux articles.
| La partie publiée du Mémoire de 1820 | Le Mémoire de 1827 |
| à lire en entier en suivant les liens (source: Gallica BnF, Œuvres
de Fourier, tome2 ) |
|
Deux autres différences méritent d'être soulignées:
- la longueur: le texte de 1827 est complet, tandis que celui de 1820 n'est qu'une petite part d'un long mémoire, sorte d'iceberg dont la part imprimée n'est, aux propres dires de l'auteur, qu' environ un dixième du tout; et la partie cachée encore à découvrir, car tous les manuscrits de Fourier sont loin d'avoir été exhumés et explorés (Jean-Pierre Kahane insistait sur la nécessité d'un travail qu'on pourrait presque qualifier d'archéologique!)
- la technicité: celui de 1827 est une rédaction "littéraire", totalement exempte de formules; au contraire celui de 1820 exhibe l'équation de la chaleur, comme les séries et les intégrales qui donnent la solution des problèmes mathématisés. Il est conçu comme une illustration (triomphante!) de sa théorie mathématique, totalement sous-tendue par la philosophie "d'utilité publique" de la science, que Fourier défendra avec brio dans la préface de la Théorie Analytique de la Chaleur , deux ans plus tard.
Application ou ... Motivation?
Fourier a l'art de distiller les indications de manière anodine... voire de nous brouiller la piste! N'annonce-t-il pas, dans le Discours Préliminaire de la Théorie Analytique, que celle-ci est littéralementconforme au ùmanuscrit de 1811, et en même temps, que ce mémoire renferme "un premier exposé des applications que ne contient pas [cet] ouvrage"? De fait, la Théorie Analytique a été amputée des trois derniers chapitres du manuscrit, probablement pour des raisons de taille, peut-être aussi pour ne pas trangresser le propos unique: dérouler une théorie mathématique de la diffusion calorique. Sont notamment passés à la trappe le chapitre XII, sur la question des températures terrestres, et le chapitre XIV, relatif aux relevés numériques des expériences. |

|
| Extrait du Discours Préliminaire faisant allusion an mémoire de 1811 et aux mémoires applicatifs à paraître | extrait du Mémoire de 1811 (Archives de l'Académie des Sciences) |
De fait, il tiendra ses promesses: le mémoire de 1820 est présenté comme une suite à la théorie mathématique élaborée en 1807-1811, une application à la physique du globe, et il ira beaucoup plus loin mathématiquement, par l'emploi non seulement des séries trigonométriques, mais aussi de la transformée intégrale du chapitre XI du manuscrit; Quant à celui de 1827, il aborde pour la première fois la question de la température "des espaces planétaires", absente du manuscrit de 1811 comme du texte de 1820. Mais une phrase, en plein milieu (!) y inverse le point de vue: ce n'est plus une simple application, mais la motivation de son travail mathématique!
| "La question des températures terrestres m'a toujours paru un des plus grands objets des études cosmologiques, et je l'avais principalement en vue en établissant la théorie mathématique de la chaleur" Fourier, Mémoire de 1827
|
Comme on le constate, elle reprend, sous une forme à peine différente, l'idée exrimée en introduction du chapitre XII du manuscrit. Mais ce qui a mené Fourier à s'intéresser à la question reste toujours largement mystérieux; sur ce point comme sur d'autres, il s'est fort peu livré. Quelle est en particulier la part de son expérience égyptienne? Par delà la différence de climat, cette aventure lui a fait prendre sconscience du problème de l'âge de la Terre, en le confrontant à celui de la datation des monuments anciens. Ambition de trancher par les mathématiques une friction possible, pour ne pas dire certaine, avec les datations bibliques?
L'autre "déclencheur" pourrait être la publication d'un mémoire de Biot en 1804, comportant une large part d'expérimentation, mais totalement dénué de modélisation mathématique. Voilà en tout cas de quoi faire le point sur les prédécesseurs de Fourier, avant de présenter une lecture commentée de ses deux écrits.
Les Prédécesseurs
Émilie du Châtelet
Née Émilie Le Tonnelier de Breteuil (1706-1749), marquise du Châtelet par alliance, cette remarquable femme de science (formée à la Physique par Maupertuis et à la Géométrie par Clairaut) rédigea le premier mémoire un peu substantiel sur le sujet de la nature du feu, mis au concours par l'Académie des Sciences en 1738. |
 |
| Portrait de la Marquise (anonyme) Remarquer le compas et la sphère armillaire. | Son Mémoire ayant concouru pour le Grand Prix de l'Académie des Sciences , en 1738 |
Elle ne gagna cependant pas, mais est-ce une défaite que s'incliner devant Euler? C'est lui dont le mémoire fut primé, sans qu'il paraisse bien meilleur sur ce coup-là. Car leurs mémoires ont les mêmes qualités et les mêmes défauts: ils témoignent d'un réel esprit scientifique, font état d'observations et d'expériences pertinentes, mais ils se trompent tous deux sur la nature de la chaleur, et surtout, ni l'un ni l'autre ne recèlent de modélisation mathématique de sa propagation. On peut déjà dire ici que le génie de Fourier sera d'esquiver la savonnette de la nature et de mathématiser la propagation.
L'Académie reconnaît d'ailleurs explicitement les qualité du mémoire de Madame du Châtelet en le faisant imprimer
|
"[...]sur
le témoignage des Commissaires du Prix, quoiqu'ils n' eussent pû
approuver l'idée que l'on donne de la nature du feu [...],
elle leur avait paru être des meilleures de celles qui avaient été
envoyées, en ce qu'elle suppose une grande lecture, & une grande
connaissance des bons ouvrages de physique, & qu'elle est remplie
de beaucoup de faits, très bien exposés, et de beaucoup de vües ."
|
Ainsi, l'auteure remarque que l'échange thermique est d'autant plus intense que la surface séparant les deux milieux est plus grande:
|
"Deux globes de Fer également échauffés, conservent leur chaleur en raison directe de leur diamètre; car plus leur diamètre est grand, moins ils ont de surface par rapport à leur masse, & moins le Feu trouve d'issüe pour s'échapper de leurs pores; & de plus, l'air extérieur qui les environne les touchant en moins de points, prend moins de leur chaleur."
|
et elle ajoute une excellente remarque, qui revient mathématiquement à ce que la sphère résout le problème isopérimétrique: elle offre le plus grand volume intérieur à surface donnée, ou, ce qui revient au même, la plus petite surface de bord à volume donné:
|
"Par la même raison, la
figure sphérique est la plus propre à conserver lon-tems la chaleur,
car c'est de toutes les figures celle qui a le moins de surface, par
rapport à sa masse. [...] Cette raison pourroit faire croire que le Soleil e& les Étoiles fixes, sont des corps sphériques (en faisant abstraction de leur force centrifuge) ."
|
Le modèle de la sphère chauffée qui se refroidit sera central dans la suite. Elle pose également les deux problèmes que Fourier reprendra et résoudra quantitativement
- La perte rapide d'influence des variations saisonnières de la température de la croûte sur la température en profondeur;
- L'augemtation de la température avec la profondeur,
et l'hypothèse d'un "feu central" pour l'expliquer... qui engendrera
boientôt le modèle de datation du globe par refroidissement.
|
"L'action [du Soleil] ne pénétre pas beaucoup au de-là de la premiere surface de la terre; on sçait que les Caves de l'Observatoire qui n'ont environ que 84. pieds de profondeur,sont d'une température égaie dans le plus grand froid & dans le plus grand chaud. Donc le Soleil n'a aucune influence à cette profondeur. [...]
Mais le froid, loin d'augmenter avec la profondeur diminuë au contraire avec elle lorsqu'elle passe de certaines bornes; c'esl ce que M. Mariotte a éprouvé en mettant le même Thermometre consécutivement dans deux Caves, l'une de 30 pieds de profondeur,& l'autre de 84; le Thermometre ne passa pas 51 degrés ½ dans la première, mais il monta à y 53 degrés ½ degrés dans la féconde Donc puisque la chaleur étoit plus grande à 84 pieds qu'à 30 il faut qu'an Feu renfermé dans les entrailles de la terre [en] soit la cause." |
Beau prélude... le travail est tout tracé pour les candidats suivants!
Buffon
 |
 |
 |

|
C'est... dans son jardin que nous découvrons un digne successeur de la marquise: le Comte de Buffon. La plaque sur sa maison, à l'entrée, nous rappelle qu'il a veillé sur lui pendant près de 50 ans, au cœur de Paris. Le naturaliste étudiee
aussi bien à la zoologie qu'à la géologie; il est donc logique qu'il
s'intéresse à la formation de la Terre; en 1749, l'année même du décès
de Mme du Châtelet. Il reprend à son compte le modèle d'une terre
chaude qui se refroidit au cours des âges, et pour mieux serrer son
sujet, entreprend une série d'expériences sur le refroidissement de 10 sphères en fer.
Il les fait soigneusement réaliser, par une forge unique afin d'assurer
une qualité constante du métal! Le protocole expérimental est également
soigné: il fait trois fois la série de mesures pour se prémunir
contre tout résultat accidentellement faussé.
Il veut d'abord montrer que le temps de refroidissement n'est pas proportionnel au diamètre N (exprimé en demi-pouces), et pour cela enregistre deux temps, le premier où la sphère peut être touchée, le second où elle est parvenue à température ambiante. Le premier est comparé à une variation proportionnelle prenant pour base le même premier temps pour la plus petite sphère. Dans la citation, nous avons remplacé le texte par un tableau pour une meilleure lisibilité. |
 Statue et maison de Buffon au Jardin des Pantes (Paris) |
||
|
"Maintenant,
si l'on vouloit chercher avec Newton, combien il faudrait de temps à un
globe gros comme la terre pour se refroidir, on trouveroit, daprès les
expériences précédentes, qu'au lieu de
50000 ans qu'il assigne pour le temps du refroidissement de la
Terre jusqu'à la température actuelle, il faudroit déjà 42964 ans &
221 jours pour la refroidir, seulement jusqu'au point où elle cesse de
brûler, & 96670 ans & 132 jours pour la refroidir à la
température actuelle.
Car la suite des diamètres des globes étant [...]"
|
||||||||||||||||||||||||||||||||||||||||||||||||
N.B. : le pouce français peut alors être évalué à 27mm, mais on ne se trompera guère en considérant que 4 pouces = 10cm pour faire les calculs de tête...
On pourra sourire de la précision -au jour près!- quand la détermination de la température de premier refroidissement, selon sa désignation dns le texte... est fort subjective. Mais avoir recours "au ministère de quatre ou cinq jolies femmes à la peau douce [...qui] tenoiant [les globes] dans leurs mains délicates, en lui rendant compte des degrés de refroidissement" (dixit le chevalier Aude, auteur d'une Vie Privée du Comte Buffon) plutôt que des... thermomètres ferait du plus réfractaire aux TP de Physique un chaud partisan des expériences répétées. Quoiqu'il en soit, Buffon n'eut pas trop de peine à trouver empiriquement de quoi aligner approximativement ces points sur deux droites, respectivement
t1 = 24 N - 12 ; t2 = 54 N - 15
(la technique aujourd'hui standard de recherche d'une droite optimale, dite des moindres carrés, n'était pas encore inventée! Ceux des lecteurs qui la connaissent, ou la trouvent dans leur tableur, pourront s'amuser à la comparaison...)
On sera à bon droit estomaqué de la suite: c'est avec ces formules déduites de sphères de rayons compris entre 1cm et 10cm que Buffon donne sa fourchette pour l'age de la Terre, en extrapolant à un rayon de 6400km! Bien conscient que le matériau peut influer, il essaie très scrupuleusement d'autres matériaux; consigne ses résultats... et se garde bien de leur donner trop de publicité: les 6000 ans de la Bible sont pulvérisés , et il n'a pas envie de finir sur la roue, sort qui fut réservé au chevalier de la Barre pour outrage à la religion, moins de dix ans (1766) avant sa publication (1774) |
 |
|
|
Statue du Chevalier de la Barre dans le square Nadar, à Montmartre (Paris).
Plutôt à l'écart des chemins
empruntés par de milliers de touristes... simple coïncidence? Non, elle
y avait été déplacée en 1926, fut fondue en 1941 (comme celle de
Fourier). L'actuel monument ne date que de 2001.
|
||
Bref, on peut faire beaucoup de choses avec de petites sphères... et ce n'est pas le célèbre sculpteur Pol Bury
(1922-2005) qui nous contredira! Dommage qu'il n'ait pas connu Buffon:
il aurait pu offrir une belle deuxième vie à sa collection de boules!
Lambert et Biot
<à compléter>
Le Refroidissement Séculaire et l'Âge de la Terre: Fourier, 1820 (et 1827)
Les deux mémoires commencent par présenter les trois influences connues sur la température de la Terre:
En effet, c'est la linéarité de l'équation qui autorise cette superposition: la somme de deux solutions est une solution, et Fourier nous rappelle que c'est ce même principe qui lui a permis de construire une solution série en sommant les solutions fondamentales très simples (les modes propres).
Admirons sa rigueur scientifique: voilà tout ce que je connais de la physique, et ma théorie est mathématiquement sûre... mais s'il y avait autre chose? Quelle belle prémonition dans ce premier message pour le futur:
C'est très exactement ce qui va se passer... avec la découverte de la radio-activité, comme on le verra plus loin. Source de chaleur ignorée de Fourier, découverte presque un siècle plus tard, qui va résoudre le problème triangulaire Fourier-Kelvin-Darwin... mais n'anticipons pas!
Nous allons poursuivre avec , essentiellement dans ce paragraphe, le Mémoire de 1820. Notre choix est dicté par deux raisons:
Voilà ce que déclare Fourier au début de son article, précisant après avoir donné une table en 11 chapitres, qu'il en développe un seul dans cette livraison du Bulletin de la Société Philomatique; sans doute lui a imposé une taille maximale. C'est dire que celu-cii lui tient à cœur... mais c'est probablement le plus relevé mathématiquement! Or justement, c'est exactement ce qu'il veut montrer, le triomphe d'une analyse exacte, fondée sur la connaissance des lois mathématiques! .
Premier modèle
Et
de jeter tout de go la monumentale, et sans doute impressionnante pour
un néophyte, formule qui résoud la question de la température à une
profondeur u, au temps t, sur une demi-droite infinie, qui "remplace"
le rayon très grand d'une sphère dont il ne va plus (momentanément
seulement) s'encombrer. La température ν (u,t) vérifie l'équation de la chaleur unidimensionnellle et une condition de déperdition au bord u=0 ; la donnée initiale est la répartition F(u), a priori arbitraire (dans la continuité de style de la Théorie Analytique de la Chaleur)

Il se montre bien plus mesuré dans les conclusions générales, se contentant de justifier l'état quasi stationnaire de la température (en raison des grandes valeurs de t, le premier et seul terme oscillant conservé est "écrasé" par son facteur exponentiel). Le jalon antique choisi est l'École d'Alexandrie, ce "point-zéro" -tel qu'il est vu à l'époque-de notre culture mathématique européenne... et la durée de refroidissement n'est plus que minorée par 80 siècles; il y a de la place entre cette estimation et les millions évoqués dans l'excès d'enthousiasme qui précède!
Et manifestement, en 1820 comme en 1827 (période qui a connu les remous de la datation du zodiaque de Dendérah), Fourier préfère une conclusion gravée dans le granit plutôt que sur le sable. Plutôt que des dates, il choisit l'éternité: ce sera donc pour affirmer que sa théorie et ses méthodes sont là, et bien là, pour toujours, dans le paysage mathématique et physique. Ces phrases seront à peu de choses près, reprises dans (pour celles de 1820), ou reprises de (pour celles de 1827) la préface de la Théorie Analytique de la Chaleur. Avec quelque chose de la fierté, sinon de l'orgueil, d'un pharaon bâtisseur de pyramides.
Appendice: pas de parachutage!
S'il est une chose que déteste l'âme mathématique du Mathouriste, c'est qu'on vous jette à la figure une formule en vous disant: vérifiez, ça marche!
Se posent alors bien des questions: comment a fait le premier qui l'a
trouvée? et si les cieux restent muets, que du haut de l'Olympe
mathématique, les dieux ne nous envoient aucun signe? Comment puis-je
me comporter face à un problème similiare?
Nous résumons ici les idées d'un accès direct, moderne, à une résolution par formule intégrale. Si les méandres de la pensée de Fourier dans la Théorie Analytique de la Chaleur offrent le charme de la croisière, que nous espérons vous avoir fait partager, une reprise synthét ique est mieux à même d'éclairer l'intérêt mathématique de la transformation de Fourier.Vous pouvez évidemment sauter sans le moindre inconvénient cet encadré si vous n'êtes pas étudiant en science ou futur ingénieur; mais ne vous arrêtez pas là, car ce palpitant roman de la Terre a encore beaucoup de belles choses à vous révéler...
Tout Seigneur (et admirateur), tout Honneur: Kelvin
William Thompson, alias Lord Kelvin (1824-1907; biographie anglaise plus complète) est considéré comme l'auteur de la première datation "moderne" de l'âge de la Terre. C'est exact en un sens, puisqu'il est le premier à avancer, sur une base scientifique, des estimations numériques qui pulvérisent le calcul biblique. Mais quant à la méthode, il ne fait qu'appliquer le travail de Fourier et ne s'en cache pas, car il est un de ses plus grands admirateurs À preuve, elle est là, dans le très réputé traité de physique co-écrit avec Tait, la célèbre phrase qui fait de la Théorie Analytique un poème... on pourrait ajouter: une épopée, et, s'agissant de l'âge de la Terre, une Légende des Siècles!
Le traitement de Kelvin est en fait légèrement différent quant à la condition au bord (il préfère supposer une croûte à température constante). Sans entrer dans le détail des calculs (le lecteur qui en est curieux peut consulter avec profit le livre de Tom Körner), les deux pages reproduites ci-dessous font clairement voir que l'équation est bien celle de Fourier, que l'intégrale de Laplace -Gauss est présente dans la solution... et qu'il n'y a pas une page où il ne rende un hommage appuyé à Fourier!
En notant λ = K/CD il obtient
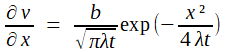 puis
puis 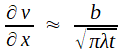
car, t étant très grand devant n'importe quel x, l'exponentielle pourra être prise égale à 1 sans ereur sensible.
Et c'est exactement ce qu'avait Fourier avec (6) et le report de sa condition initiale! Mais Kelvin fait, lui, l'application numérique... et voici ce qu'il trouve
Une objection plus sérieuse va venir d'un jeune chercheur qui s'est nourri des traités de Lyell, et en qui il trouvera un des premiers défenseurs de sa théorie de l'évolution des espèces: Charles Darwin (1802-1889). Même la durée la plus longue qu'ait proposée Kelvin est, selon lui, très insuffisante pour que se soient réalisés les lentes mutations décrites dans L'Origine des espèces (1859). Les nombreux détracteurs de la nouvelle théorie ne manquent d'ailleurs pas de lui opposer un Kelvin, alors considéré comme la grande autorité du monde savant, mais qui, au fil des éditions du Traité de Philosophie Naturelle, s'avoue profondément troublé par cette contradiction qu'il ne parvient pas à résoudre.
Ils ont immédiatement compris qu'une méthode de datation des échantillons de roches s'en déduit, qui va changer l'ordre de grandeur retenu par Kelvin -qui a accueilli l'article dans le Philosophical Magazine qu'il dirige: notre "bonne vieille Terre" va se retrouver d'un seul coup bien plus âgée, l'ordre de grandeur passant des millions aux milliards d'années (estimation actuelle :4,55 milliards d'années). La contradiction apparante avec l'étude du refroidissement est levée, car la décomposition radioactive s'accompagne d'une formidable libération d'énergie. Il ne reste pour Rutherford qu'à faire passer la chose avec diplomatie... surtout lorsque Kelvin est dans la salle, comme c'est le cas pour une conférence donnée en 1904:
A-t-il vu en songe Fourier le lui souffler? Rappelez-vous ce qu'il disait au début de son mémoire, en séparant les diverses causes des échanges thermiques:
Autres thèmes développés dans les deux Mémoires de Fourier (1820, 1827)
Ce qui procède d'un souci, au demeurant légitime, d'équilibre thermique entre la terre et son milieu environnement: il pense que sinon, la terre perdrait beaucoup trop de sa chaleur et ne pourrait maintenir à sa surface les températures qu'on y relève. Mais il sous-estime grandement, à ce moment précis, le rôle de couche isolante que constitue l'atmosphère, et sur lequel il va revenir avec la plus grande pertinence quelques pages plus loin.
Un homme dont le génie est toujours à l'affut de l'actualité va graver dans le marbre, ou du moins dans un de ses romans, l'erreur de Fouirer: Jules Verne! En 2019, pour les 150 ans de sa prmeière publication... et les 50 ans des premiers pas de Neil Armstrong et Buzz Aldrin sur la lune, ont été réédités à la fois un fac-simile de l'édition Hetzel et même le manuscrit original
En fait, ils se trompent tous les deux: nous savons aujourd'hui que cette température est encore bien plus basse, proche de -270°C, soit 3°C au dessus du zéro absolu: c'est celle du rayonnement fossile de l'Univers, signature du Big Bang. Une valeur à peu près inimaginable à l'époque des deux savants... Il faudra attendre le début du XXème siècle pour approcher vraiment le zéro absolu au laboratoire ( le Mathouriste ne résite pas au plaisir de vous faire voir le lieu et le héros de l'aventure) et le 20 mai1964 pour la découverte indiscutable du rayonnement fossile, conjecturé depuis 1948, par les physiciens américains Arno Penzias et Robert Woodrow Wilson. La difficulté du sujet offre donc quelques excuses aux malheureuses estimations de Fourier et Pouillet!
Rendons à chacun son mérite: à De Saussure, l'envie de'expliquer l'échauffement à travers les vitres (d'où la multiplication des couches dans l'appareil de son invention), à Fourier l'idée géniale du rôle comparable de l'atmosphère. Mais il faut en préalable mieux comprendre le phénomène, et Fourier le résume ainsi:
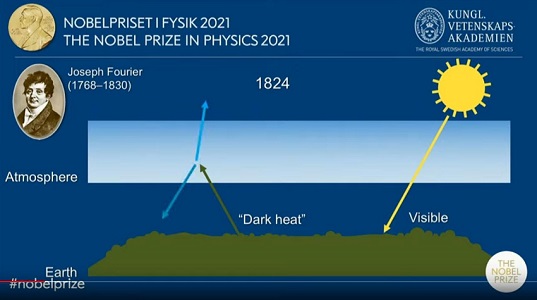
Qu'est-ce donc que cette chaleur obscure? Ce que l'on n'appelle pas encore, au temps de Fourier, rayonnement infrarouge. Il est découvert en 1800 par l'astronome Willima Herschel, qui cherchait à mesurer les températures des rayons de différentes couleurs séparés par un prisme, à partir d'une lumière blanche, et constata l'élévation de la température dans la zone d'ombre proche de la partie rouge. L'absence de lumière visible associée vient expliquer cette dénomination historique. Quant au matériel expérimental, le Mathouriste a pu le voir dans la maison de William Herschel, à Bath. C'est aujourd'hui un beau petit musée dont il vous recommande la visite!
Le pas supplémentaire que fait Fourier est de comprendre que l'atmosphère joue partiellement, pour la terre, le rôle du vitrage:
Dit de façon un peu plus moderne: l'énergie reçue du rayonnement solaire par la terre est partiellement réémise (conformément à la thermodynamique, vers l'atmosphère plus froide) sous forme de rayonnement infrarouge. Lequel peut être y retenu par les gaz qui y sont présents et possèdent une grande capacité d'absorption dans la partie infrarouge: ils retiendront et réémétront cette chaleur vers la terre, apportant ainsi un supplément calorique. Ce sont les désormais (malheiureusement) célèbres gaz à effet de serre, que recense déjà le chimiste suédois Svante Arrhenius (1859-1927, prix Nobel 1903), tout en rendant hommage à ses prédécesseurs, et, au tout premier rang, à Fourier:
Il mérite qu'on le cite un peu plus largement ici, tant sa pensée apparaît comme le meilleur prolongement de celle de Fourier. La vapeur d'eau et le gaz carbonique sont les principaux responsables: en un sens, c'est heureux, car sinon la terre serait beaucoup plus froide... donc moins habitable! Arrhenius évalue (à lui tout seul, bien avant qu'une cohorte d'experts du GIEC s'attèle, avec plus de précision sans doute, à la même tâche) les effets de la quantité de CO2 (alors nommée acide carbonique) rejetée
Sa conclusion est remarquable pour l'époque: il a compris la fragilité de l'équilbre naturel, qui n'a rien d'acquis de toute éternité (on sort tout juste du petit âge glaciaire, qu'il commente longuement), et le risque d'aller vers un dérèglement climatique. Il pointe avec un siècle d'avance une gestion des ressources insouciante de l'avenir et les dangers d'une démographie galopante. Sa conclusion -il veut croire en un monde meilleur-peut certes sembler naïve, du moins exagérément optimiste aujourd'hui, d'autant qu'elle ne prend pas en compte l'effet d'une désertification dans les pays du Sud; mais à le replacer dans son époque, on salueara la pertinence de ses idées générales.
Or, rien de tout cela n'avait pas échappé à Fourier, un siècle avant exactement (si l'on prend pour référence le dépôt de son premier mémoire à l'Académie), et c'est d'autant plus méritoire que, dans son cas, la révolution industrielle était encore à venir! Sans oublier, lui non plus, les aleas naturels, li mentionnait deux fois la contribution anthropique dans le Mémoire de 1827, à près de dix pages d'écart. Il ne faisait que reprendre une idée non moins clairement exprimée dans celui de 1820.
C'est un beau et fort symbole de voir qu'aujourd'hui, que ce soit depuis la terre ou des stellites (la sonde Cassini par exemple), la télésurveillance des gaz à effet de serre dans l'atmosphère repose sur la spectroscopie infrarouge par transformation de Fourier (à découvrir en détails dans notrre page sur les applications en spectroscopie). La transformation rapide, bien entendu, sinon nos meilleurs ordinateurs seraient submergés sous le volume des calculs...
Et nous ne sommes pas les seuls à le dire; regardez la présentation à la presse des Prix Nobel de Physique 2021: pour introduire les travaux de Syukuro Manabe et Klaus Hasselmann (récipiendaires chacun d'un quart du prix), John Wettlaufer, membre du Comité Nobel pour la Physique, revient à... Fourier!
Syukuro Manabe a construit, en 1967, le premier modèle global du climat prenant en compte l'effet de serre et la convection; il est considéré comme un pionnier du traitement informatique du problème. 10 ans plus tard Klaus Hasselmann expliquait pourquoi l'on peut prédire l'évolution du climat malgré le caractère chaotique de la météorologie ( il nous paraît important de rappeler ici que la découverte du chaos météorologique par Lorenz repose sur l'utilisation de développements de Fourier, voir notre page).
Au fait, le savez-vous? Certains d'entre vous, chers lecteurs, voient chaque jour un écho artistique du modèle de Manabe... dans la station RER de la gare du Nord! L'artiste britannique Liam Gillick a "décoré" les murs de béton, à la demande de la SNCF, en s'inspirant librement des formules de son article; ce qui compte pour lui est l'esthétique des caractères mathématiques, et non leur sens; il réagit au texte comme nous pouvons être sensibles aux textes en langue arabe (si nous ignorons tout de la langue) qui décorent les murs des mosquées.
Fourier nous a aussi fourni les mathématiques de notre outillage de détection; et si bien sûr, il ne pouvait s'en douter, il ne cessait de réaffirmer le caractère pérenne d'une théorie qui appartiendrait pour toujours aux sciences mathématiques. La jeunesse et l'efficacité de la spectroscopie par transformée de Fourier montrent que cette confiance en son œuvre n'était en rien trop orgueilleuse.
Mais Fourier ne peut pas tout pour nous, à notre place de citoyens du monde. Nous avons trouvé un sage pour dire, mieux que nous ne le ferions, ce qu'il laisse à notre responsabilité collective. On s'inquiètera légitimement de ce que ce discours fut prononcé 30 ans avant que cette page ne soit écrite, qu'il ne sera pas difficile de décomposer en septennats et quinquennats.
Lambert et Biot
<à compléter>Le Refroidissement Séculaire et l'Âge de la Terre: Fourier, 1820 (et 1827)
Les deux mémoires commencent par présenter les trois influences connues sur la température de la Terre:- l'action radiative du Soleil;
- l'existence d'une chaleur interne initiale qui se dissipe au fil du temps;
- l'échange avec l'espace interstellaire.
| " [...] nous avons d'abord à exprimer une remarque qui s'étend à toutes ces parties, parce qu'elle est fondée sur la nature des équations différentielles du mouvement de la chaleur. Elle consiste en ce que les effets qui proviennent de chacune des trois causes que l'on a indiquées peuvent être calculés séparément, comme si chacune de ces causes existait seule. Il suffit ensuite de réunir les effets partiels; ils se superposent librement comme les dernières oscillations des corps." Fourier, Mémoire de 1827
|
En effet, c'est la linéarité de l'équation qui autorise cette superposition: la somme de deux solutions est une solution, et Fourier nous rappelle que c'est ce même principe qui lui a permis de construire une solution série en sommant les solutions fondamentales très simples (les modes propres).
Admirons sa rigueur scientifique: voilà tout ce que je connais de la physique, et ma théorie est mathématiquement sûre... mais s'il y avait autre chose? Quelle belle prémonition dans ce premier message pour le futur:
| "Si d'autres causes jusqu'ici ignorées peuvent expliquer les mêmes faits, et s'il existe d'autres sources ou générales ou accidentelles de la chaleur terrestre, on les découvrira par la comparaison des résultats de cette théorie avec ceux des observations." Fourier, Mémoire de 1820
|
C'est très exactement ce qui va se passer... avec la découverte de la radio-activité, comme on le verra plus loin. Source de chaleur ignorée de Fourier, découverte presque un siècle plus tard, qui va résoudre le problème triangulaire Fourier-Kelvin-Darwin... mais n'anticipons pas!
Nous allons poursuivre avec , essentiellement dans ce paragraphe, le Mémoire de 1820. Notre choix est dicté par deux raisons:
- Nous profitons de l'occasion pour disséquer un peu les mathématiques qu' emploie Fourier -et pas seulement, on le verra, celles de la Théorie Analytique de la Chaleur ;
- Le Mémoire de 1827 fait l'objet d'une présentation sur le site BibNum écrite par James Lequeux, et nous nous en voudrions de recourir au pillage ou au remake... dans une moins bonne version! (C'est hélas le sort le plus fréquent des remakes). Nous vous la conseillons de toute manière, que ce soit en lieu et place, ou en complément.
| "Le troisième mouvement de la chaleur est variable, et il produit le refroidissement séculaire du globe. Cette
chaleur qui se dissipe ainsi dans les espaces planétaires était propre
à la Terre, et primitive; elle est due aux causes qui subsistaient à
l'origine de cette planète; elle abandonne lentement les masses intérieures, qui conservent pendant un temps immense une température très élevée. Cette hypothèse d'une chaleur intérieure et centrale s'est renouvelée dans tous les âges de la Philosophie, car elle se présente d'elle-même à l'esprit comme la cause naturelle de plusieurs phénomènes. La question consistait à soumettre
l'examen de cette opinion à une analyse exacte, fondée sur la
connaissance des lois mathématiques de la propagation de la chaleur. C'est ce mouvement variable de la chaleur primitive du globe qui est l'objet principal du Mémoire dont nous donnons l'extrait [...]" Fourier, Mémoire de 1820
|
Voilà ce que déclare Fourier au début de son article, précisant après avoir donné une table en 11 chapitres, qu'il en développe un seul dans cette livraison du Bulletin de la Société Philomatique; sans doute lui a imposé une taille maximale. C'est dire que celu-cii lui tient à cœur... mais c'est probablement le plus relevé mathématiquement! Or justement, c'est exactement ce qu'il veut montrer, le triomphe d'une analyse exacte, fondée sur la connaissance des lois mathématiques! .
Premier modèle
Et
de jeter tout de go la monumentale, et sans doute impressionnante pour
un néophyte, formule qui résoud la question de la température à une
profondeur u, au temps t, sur une demi-droite infinie, qui "remplace"
le rayon très grand d'une sphère dont il ne va plus (momentanément
seulement) s'encombrer. La température ν (u,t) vérifie l'équation de la chaleur unidimensionnellle et une condition de déperdition au bord u=0 ; la donnée initiale est la répartition F(u), a priori arbitraire (dans la continuité de style de la Théorie Analytique de la Chaleur)
D'une
part, renvoyer au Mémoire de 1807 est quelque peu étonnant: à
l'évidence, la formule est une application de la transformation
intégrale de Fourier, qui n'apparaît qu'en 1811, et au chapitre IX de
la Théorie Analytique. D'autre part, Darboux, qui édite les Œuvres sans apporter beaucoup d'éclaircissements, se croît tout de même obligé de la justifier, ou plus exactement , de la vérifier.
On peut faire la même chose, en plus simple encore, si l'on observe que Fourier se limite ensuite au cas physiquement le plus utile: F(u) = b ; c'est à dire que la température initiale de la Terre est la même à toute profondeur, quand elle n'est qu'une boule homogène de lave en fusion que vient de "pondre" le soleil brûlant qui lui a communiqué sa température interne. C'est à la fois simple et de bon sens; on peut du coup remplacer l'intégrale la plus à droite par..b, sans précaution particulière de calcul
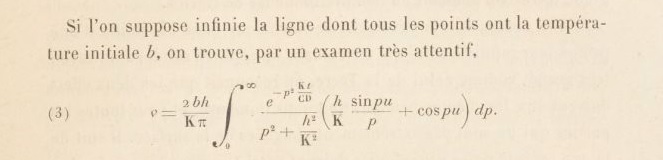
En effet, l'expression est de la forme (il est toujours très important de dégager des esxpressions compliquées ce que nous voulons voir en oubliant -temporairement!- tout ce qui pourrait nous gêner autour...)
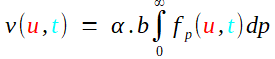 avec
avec 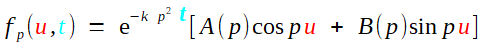
cela rend évident que fp vérifie l'équation de la chaleur (faire deux calculs séparés pour cos et sin et user de la linéarité) qui s'écrit avec ces noms de variables
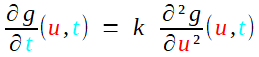
Il s'en suit que l'intégrale la vérifie aussi, comme somme de termes élémentaires la vérifiant, nous dirait Fourier avec un naturel eulérien; mais c'est bien sûr une dérivation sous le signe somme, facile à justifier pour t>0. ( Darboux ne se donne pas plus de mal, c'est encore trop tôt!) . Quant à retrouver la valeur b pour t=0, c'est la simple utilisation du calcul des transformées de Fourier en sin ou cos que le maître a obtenues dans le mémoire principal de 1811 (à retrouver aux pages 434-435 de la Théorie Analytique; nous les avons montrées dans la page relatant la naissance de la transformation intégrale).
Le moment le plus virtuose arrive ensuite! En deux "passages" d'une ligne à l'autre, ci-dessous (4)---> (5) et (5)---> (6), on va découvrir un mathématicien qui maîtrise son sujet... tout en chaussant ses bottes de sept lieues!. On peut se demander quelle proportion d'étudiants de niveau L2/Mathématiques Spéciales, ayant les bases ad hoc pour le faire, y arriveront en autonomie complète, sans indication... De quoi faire taire tous ceux qui feraient une moue sceptique sur ses talents en la matière.

Voici le détail de ces deux manipulations, que les âmes sujettes au vertige intégral peuvent sauter sans inconvénient pour admettre la formule très simple (6).dont nous reparlerons.
On peut faire la même chose, en plus simple encore, si l'on observe que Fourier se limite ensuite au cas physiquement le plus utile: F(u) = b ; c'est à dire que la température initiale de la Terre est la même à toute profondeur, quand elle n'est qu'une boule homogène de lave en fusion que vient de "pondre" le soleil brûlant qui lui a communiqué sa température interne. C'est à la fois simple et de bon sens; on peut du coup remplacer l'intégrale la plus à droite par..b, sans précaution particulière de calcul
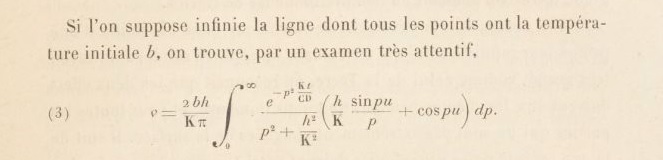
En effet, l'expression est de la forme (il est toujours très important de dégager des esxpressions compliquées ce que nous voulons voir en oubliant -temporairement!- tout ce qui pourrait nous gêner autour...)
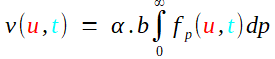 avec
avec 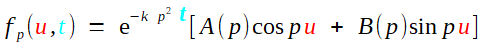
cela rend évident que fp vérifie l'équation de la chaleur (faire deux calculs séparés pour cos et sin et user de la linéarité) qui s'écrit avec ces noms de variables
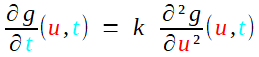
Il s'en suit que l'intégrale la vérifie aussi, comme somme de termes élémentaires la vérifiant, nous dirait Fourier avec un naturel eulérien; mais c'est bien sûr une dérivation sous le signe somme, facile à justifier pour t>0. ( Darboux ne se donne pas plus de mal, c'est encore trop tôt!) . Quant à retrouver la valeur b pour t=0, c'est la simple utilisation du calcul des transformées de Fourier en sin ou cos que le maître a obtenues dans le mémoire principal de 1811 (à retrouver aux pages 434-435 de la Théorie Analytique; nous les avons montrées dans la page relatant la naissance de la transformation intégrale).
Le moment le plus virtuose arrive ensuite! En deux "passages" d'une ligne à l'autre, ci-dessous (4)---> (5) et (5)---> (6), on va découvrir un mathématicien qui maîtrise son sujet... tout en chaussant ses bottes de sept lieues!. On peut se demander quelle proportion d'étudiants de niveau L2/Mathématiques Spéciales, ayant les bases ad hoc pour le faire, y arriveront en autonomie complète, sans indication... De quoi faire taire tous ceux qui feraient une moue sceptique sur ses talents en la matière.

Voici le détail de ces deux manipulations, que les âmes sujettes au vertige intégral peuvent sauter sans inconvénient pour admettre la formule très simple (6).dont nous reparlerons.
| Explications complémentaires On cherche à mettre le dénominateur sous la forme : 1+q² (la forme, toujours la forme... pour y voir clair!). On factorise donc h²/K² au dénominateur, que l'on ventile "moitié/moitié" du côté de la constante d'une part, pour la simplifier, et du dp d'autre part, pour faire apparaître le dq au moindre effort: 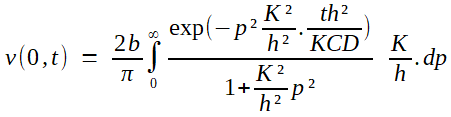 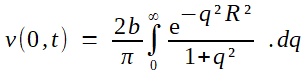 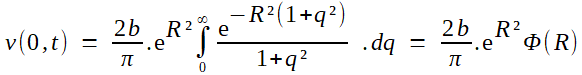 Il n'y a plus alors qu'à transformer la fonction Φ(R); sa forme invite très naturellement à une dérivation sous le signe intégrale qui ne peut que la simplifier en vue du calcul (R n'étant pas nul, toutes les hypohèses requises pour une telle popération se vérifient très aisément)
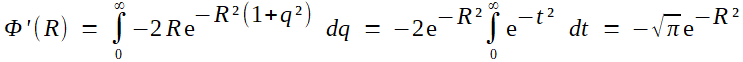 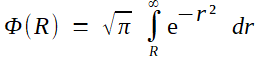 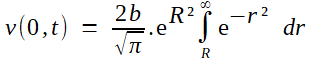 (5)---> (6) Cette expression était exacte. Maintenant, Fourier va passer à une expression approchée par développement asymptotique de l'intégrale. On effectue pour cela une intégration par parties, en forçant l'apparition de la dérivée de exp(-r²) et en compensant multiplicativement: 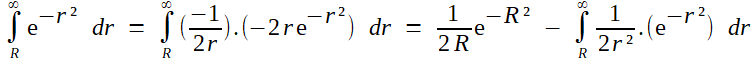 Il ne restera dès lors quà montrer que le deuxième terme est négligeable devant le premier. Ou, petit trick qui revient au même, le passer au premier membre et montrer qu'il est négligeable devant l'intégrale étudiée; mais c'est alors évident en majorant 1/r² par 1/R². Fourier est donc fondé à conserver seulement le terme exp(-R²) /2 R ... et voilà pourquoi le "2" a disparu de la formule! 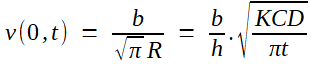 |
Revenons à Fourier, qui conclut:
Incroyablement, alors qu'il donne des valeurs raisonnables au seul paramètre restant, le rapport CD/K, il ne va pas plus loin... et toute la gloire sera pour Kelvin.
| "Ainsi la
température de la surface varie en raison inverse de la racine carrée
des temps écoulés depuis le commencement du refroidissement. La
valeur du temps t étant devenue beaucoup plus grande que mille années,
c'est cette équation (6) qui exprime, en fonction de t et des
constantes K, C, D, h, la température variable v de la surface du globe
terrestre, pendant un nombre immense de siècles. " Fourier, Mémoire de 1820
|
Deuxième modèle
Pourtant, il ne s'en tient pas là: après tout, la terre est une sphère de grand rayon, mais pas un plan à la verticale duquel on s'enfonce à l'infini. Dès lors, pourquoi ne pas se servir de l'étude de la sphère réalisée dans les mémoires de 1807 et 1811, et corroborer par cette deuxième méthode le résultat qu'il vient d'obtenir? (le mot intégrale doit ici être compris au sens de solution, courant à l'époque)
| "Si
l'on compare le mouvement de la chaleur dans un solide d'une profondeur
infinie à celui qui a lieu dans une sphère solide, d'un rayon très
grand, comme celui de la Terre, on reconnaît que les deux effets
doivent être les mêmes pendant un temps immense, et pour toutes les
parties qui ne sont pas extrêmement éloignées de la surface. Il suit de
là que les intégrales précédentes
doivent aussi être données par les formules qui expriment le mouvement
variable de la chaleur dans une sphère d'un rayon quelconque. " Fourier, Mémoire de 1820
|
 |
 |
Il rappelle donc les équations pour la sphère et les résultats obtenus dans ce qui deviendra le chapitre V de la Théorie Analytique. (voir notre page dédiée). On y somme en série des fonctions de la forme B(pi). exp [-pi²t K/(CD) ] . sin (pix )
Puis il indique, assez allusivement (et rapidement) que, lorsque le
rayon de la sphère tend vers l'infini, cette somme se transforme en
intégrale; on l'a vu faire un travail similaire pour justifier sa
transformation intégrale. |
|
||
| recomposition des pp. 278&279 du Mémoire (Œuvres, t;2) |
p. 280 du Mémoire (Œuvres, t;2) |
Et les Applications Numériques?
Celui qui a accompagné son étude mathématique générale de tant d'expériences, ici, se dérobe... et laissera un autre cueillir le fruit mûr de son travail! L'argument est certes légitime: il ne dispose pas de bonnes valeurs expérimentales des constantes dont il a besoin. La conclusion sera plus prudente, mais ce sera l'occasion de souligner que les déterminations ultérieures ne remettront pas en cause un modèle mathématique à qui il promet une validité éternelle!| "On ne connaît point la densité des couches intérieures du globe, ni les valeurs des coefficients K, h.
Ces deux derniers coefficients n'ont été déterminés jusqu'ici que pour
une seule substance, le fer forgé dont la surface serait polie. Les
expériences que nous avons faites pour mesurer ces coefficients ne se
rapportaient point à la question actuelle; elles avaient pour objet de
comparer quelques résultats théoriques avec ceux des observations, et
surtout de déterminer, du moins pour une substance, les éléments
qu'exigent les applications numériques. Nous ne pouvons donc
aujourd'hui appliquer les formules précédentes qu'à une sphère solide
de fer, d'un rayon comparable à celui de la Terre; mais cette
application donne une idée exacte et complète des phénomènes. Il est
facile ensuite de modifier les solutions générales, en supposant que
les coefficients D, C, h, K varient avec l'espèce de la matière, avec
la profondeur, la pression et la température.[...] Toutefois il est nécessaire de remarquer que ces conséquences ne sont entièrement exactes que si on les rapporte à une sphère de fer solide et homogène, d'un diamètre égal à celui de la Terre. Notre objet est moins de discuter les applications spéciales de la théorie à la masse du globe terrestre, dont la constitution intérieure nous est inconnue, que d'établir les principes mathématiques de cet ordre de phénomènes. " Fourier, Mémoire de 1820
|
Incroyablement, alors qu'il donne des valeurs raisonnables au seul paramètre restant, le rapport CD/K, il ne va pas plus loin... et toute la gloire sera pour Kelvin.
Et l'âge de la Terre?
Dans le cadre du modèle sphérique, où la solution est décrite par une série de termes exp (-k pi²t).sin (pix), il rappelle d'abord que la comparaison relative des exponentielles permet très vite de considérer comme une suffisante l'approximation qui consiste à ne conserver que la première d'entre elles, avant d'affirmer tout de go qu'eu égard à la taille de la terre, ce temps doit défier toute valeur jusque là avancée:| "Une des conséquences de cette solution consiste en ce que le mouvement de la chaleur dans l'intérieur du solide devient de plus en plus simple, à mesure que le temps augmente. Lorsque le refroidissement a duré pendant un certain temps que l'on peut déterminer, l'état variable du solide est exprimé sans erreur sensible par le premier terme de la valeur de p [...] Nous avons reconnu, en èffet, dans nos expériences, que cette disposition finale et régulière des températures s'établit, dans les corps de dimensions médiocres, après un temps assez court. Mais, pour une sphère solide d'un rayon comparable à celui de la Terre, les rapports des températures ne deviendraient fixes qu'après un temps immense, [...] durée qui doit surpasser plusieurs millions de siècles. Fourier, Mémoire de 1820
|
Il se montre bien plus mesuré dans les conclusions générales, se contentant de justifier l'état quasi stationnaire de la température (en raison des grandes valeurs de t, le premier et seul terme oscillant conservé est "écrasé" par son facteur exponentiel). Le jalon antique choisi est l'École d'Alexandrie, ce "point-zéro" -tel qu'il est vu à l'époque-de notre culture mathématique européenne... et la durée de refroidissement n'est plus que minorée par 80 siècles; il y a de la place entre cette estimation et les millions évoqués dans l'excès d'enthousiasme qui précède!
| "Quant
au nombre de siècles écoulés depuis l'origine du refroidissement il est évident qu'on ne peut l'assigner; mais on est du
moins certain qu'il surpasse la durée des temps historiques, telle
qu'on peut la connaître aujourd'hui par les annales authentiques les
plus anciennes: ce nombre n'est donc pas moindre que soixante ou
quatre-vingts siècles. On en conclut, avec certitude, que l'abaissement
de la température pendant un siècle est plus petit que d'un degré
centésimal. Depuis l'École grecque d'Alexandrie jusqu'à nous, la
déperdition de la chaleur centrale n'a pas occasionné un abaissement
thermométrique d'un 288e de degré. Les températures de la superficie du
globe ont diminué autrefois, et elles ont subi des changements très
grands et assez rapides; mais cette cause a, pour ainsi dire, cessé
d'agir à la surface: la longue durée du phénomène en a rendu le
progrès insensible, et le seul fait de cette durée suffit pour prouver
la stabilité des températures." Fourier, Mémoire de 1820
|
Et manifestement, en 1820 comme en 1827 (période qui a connu les remous de la datation du zodiaque de Dendérah), Fourier préfère une conclusion gravée dans le granit plutôt que sur le sable. Plutôt que des dates, il choisit l'éternité: ce sera donc pour affirmer que sa théorie et ses méthodes sont là, et bien là, pour toujours, dans le paysage mathématique et physique. Ces phrases seront à peu de choses près, reprises dans (pour celles de 1820), ou reprises de (pour celles de 1827) la préface de la Théorie Analytique de la Chaleur. Avec quelque chose de la fierté, sinon de l'orgueil, d'un pharaon bâtisseur de pyramides.
| Fourier, Mémoire de 1820 |
Fourier, Mémoire de 1827 |
| "Nous ajoutons, en terminant cet Extrait, que les valeurs numériques qui y sont rapportées ne peuvent être regardées comme exactes, ou même comme très approchées; car elles sont sujettes à toutes les incertitudes des observations. Mais il n'en est pas de même des principes de la théorie; ils sont exactement démontrés et indépendants de toute hypothèse physique sur la nature de la chaleur. Cette cause générale est assujettie à des lois mathématiques immuables, et les équations différentielles sont les expressions de ces lois." | "Dans
le présent écrit, je me suis proposé un autre but, celui d'appeler
l'attention sur un des plus grands objets de la Philosophie naturelle,
et de présenter les vues et les conséquences générales. J'ai
espéré que les géomètres ne verraient pas seulement dans ces recherches
des questions de calcul, mais qu'ils considéreraient aussi l'importance
du sujet. On ne pourrait point aujourd'hui résoudre tous les
doutes dans une matière aussi étendue, qui comprend, outre les
résultats d'une analyse difficile et nouvelle, des notions physiques
très variées. On multipliera par la suite les observations exactes; on
étudiera les lois du mouvement de la chaleur dans les liquides et dans
l'air. On découvrira peut-être d'autres propriétés de la chaleur
rayonnante, ou des causes qui modifient les températures du globe. Mais
toutes les lois principales du mouvement de la chaleur sont connues;
cette théorie, qui repose sur des fondements invariables, forme une
nouvelle branche des Sciences mathématiques: elle
se compose aujourd'hui des équations différentielles du mouvement de la
chaleur dans les solides et dans les liquides, des intégrales de ces
premières équations et des théorèmes relatifs à l'équilibre de la
chaleur rayonnante." |
Appendice: pas de parachutage!
S'il est une chose que déteste l'âme mathématique du Mathouriste, c'est qu'on vous jette à la figure une formule en vous disant: vérifiez, ça marche!
Se posent alors bien des questions: comment a fait le premier qui l'a
trouvée? et si les cieux restent muets, que du haut de l'Olympe
mathématique, les dieux ne nous envoient aucun signe? Comment puis-je
me comporter face à un problème similiare?Nous résumons ici les idées d'un accès direct, moderne, à une résolution par formule intégrale. Si les méandres de la pensée de Fourier dans la Théorie Analytique de la Chaleur offrent le charme de la croisière, que nous espérons vous avoir fait partager, une reprise synthét ique est mieux à même d'éclairer l'intérêt mathématique de la transformation de Fourier.Vous pouvez évidemment sauter sans le moindre inconvénient cet encadré si vous n'êtes pas étudiant en science ou futur ingénieur; mais ne vous arrêtez pas là, car ce palpitant roman de la Terre a encore beaucoup de belles choses à vous révéler...
| La Transformée de Fourier au service des Équations aux Dérivées Partielles <à
venir>
|
Les Suiveurs: Kelvin, Darwin et les Autres...
Tout Seigneur (et admirateur), tout Honneur: Kelvin
 |
 |  |
 |
| statue
de Kelvin à Kelvingrove Park, Glasgow (près de l'Université, dont sont
probablement issus les petits plaisantins qui lui offert ce chapeau) |
|||
William Thompson, alias Lord Kelvin (1824-1907; biographie anglaise plus complète) est considéré comme l'auteur de la première datation "moderne" de l'âge de la Terre. C'est exact en un sens, puisqu'il est le premier à avancer, sur une base scientifique, des estimations numériques qui pulvérisent le calcul biblique. Mais quant à la méthode, il ne fait qu'appliquer le travail de Fourier et ne s'en cache pas, car il est un de ses plus grands admirateurs À preuve, elle est là, dans le très réputé traité de physique co-écrit avec Tait, la célèbre phrase qui fait de la Théorie Analytique un poème... on pourrait ajouter: une épopée, et, s'agissant de l'âge de la Terre, une Légende des Siècles!
|
"[...]La distribution de chaleur à cet âge éloigné est essentiellement initiale - c'est à dire qu'elle n'est le résultat d'aucun état antérieur de la matière par un processus naturel. Elle est donc à juste titre dénommée «distribution initiale arbitraire de la chaleur» dans le grand poème mathématique de Fourier,
parce que ce qui est exprimé avec rigueur par la formule mathématique
ne pourrait être réalisé que par l'intervention d'une puissance capble
de modifier les lois de la matière inerte."
Thomson & Tait, Traité de Philosophie Naturelle, vol.I, part.II, app.D, p.470 (édition de 1883)
|
Le traitement de Kelvin est en fait légèrement différent quant à la condition au bord (il préfère supposer une croûte à température constante). Sans entrer dans le détail des calculs (le lecteur qui en est curieux peut consulter avec profit le livre de Tom Körner), les deux pages reproduites ci-dessous font clairement voir que l'équation est bien celle de Fourier, que l'intégrale de Laplace -Gauss est présente dans la solution... et qu'il n'y a pas une page où il ne rende un hommage appuyé à Fourier!
 |
 |
| "Thomson & Tait, Traité de Philosophie Naturelle, vol.I, part.II, app.D (édition de 1883) |
|
En notant λ = K/CD il obtient
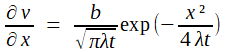 puis
puis 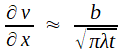
Et c'est exactement ce qu'avait Fourier avec (6) et le report de sa condition initiale! Mais Kelvin fait, lui, l'application numérique... et voici ce qu'il trouve
|
"Si nous supposons que la température de la roche en fusion est 10.000°F [5538°C, NdT] (ce qui nous paraît très surestimé), la solidification a dû commencer il y a 200 millions d'années. Ou, si nous supposons que cette température de la roche en fusion est 7.000°F [3871°C, NdT] (ce qui est une valeur plus communément admise), on peut penser que le processus de solidification a duré 98 millions d'années."
|
De Darwin à Rutherford
Mais dès les années 1830-1840, des géologues comme Charles Lyell se demandent si ces temps ne sont pas encore trop courts pour la formation des couches géologiques. Dans son travail, Kelvin lui-même souhaite que des connaissances plus précises sur les roches viennent améliorer les constantes requises par son modèle, et ses propres estimations ont été déduites de l'étude de divers échantillons. En même temps, il considère comme possible que les couches se soeient formées beaucoup plus rapidement à température élevée, ce qui léverait l'objection potentielle à son modèle.Une objection plus sérieuse va venir d'un jeune chercheur qui s'est nourri des traités de Lyell, et en qui il trouvera un des premiers défenseurs de sa théorie de l'évolution des espèces: Charles Darwin (1802-1889). Même la durée la plus longue qu'ait proposée Kelvin est, selon lui, très insuffisante pour que se soient réalisés les lentes mutations décrites dans L'Origine des espèces (1859). Les nombreux détracteurs de la nouvelle théorie ne manquent d'ailleurs pas de lui opposer un Kelvin, alors considéré comme la grande autorité du monde savant, mais qui, au fil des éditions du Traité de Philosophie Naturelle, s'avoue profondément troublé par cette contradiction qu'il ne parvient pas à résoudre.
La découverte de la
radioactivité par Becquerel, Marie et Pierre Curie (1897) va
précipiter le coup de grâce à la théorie "fouriériste" de
Kelvin.. Le physicien Ernest Rutherford
(1871 –1937, prix Nobel 1908) se lance dans la course
expérimentale. La métaphore est sienne: ce grand sportif et rugbuyman
accompli écrit dans une lettre à sa mère en 1901:
Il s'est adjoint le chimiste Frederick Soddy ( prix Nobel 1921); leur complémentarité en fait une équipe terriblement efficace, et dès 1903 ils sont en mesure de publier un article essentiel: ils y énoncent la loi de décroissance exponentielle de la radioactivité et définissent la période radioactive d'un élément. Sans oublier de rendre hommage à leurs prédécesseurs: Sportivement... mais dans un style plus académique, bien sûr. |
  Au musée Curie à Paris, le Radium, Pierre et Marie attendent votre visite! |
|
|
||
 |
 |
|
Cet article est présenté et commenté en détail par Pierre Radvanyi pour BibNum.
|
|
Ils ont immédiatement compris qu'une méthode de datation des échantillons de roches s'en déduit, qui va changer l'ordre de grandeur retenu par Kelvin -qui a accueilli l'article dans le Philosophical Magazine qu'il dirige: notre "bonne vieille Terre" va se retrouver d'un seul coup bien plus âgée, l'ordre de grandeur passant des millions aux milliards d'années (estimation actuelle :4,55 milliards d'années). La contradiction apparante avec l'étude du refroidissement est levée, car la décomposition radioactive s'accompagne d'une formidable libération d'énergie. Il ne reste pour Rutherford qu'à faire passer la chose avec diplomatie... surtout lorsque Kelvin est dans la salle, comme c'est le cas pour une conférence donnée en 1904:
A-t-il vu en songe Fourier le lui souffler? Rappelez-vous ce qu'il disait au début de son mémoire, en séparant les diverses causes des échanges thermiques:
| "Si d'autres causes jusqu'ici ignorées peuvent expliquer les mêmes faits, et s'il existe d'autres sources ou générales ou accidentelles de la chaleur terrestre, on les découvrira par la comparaison des résultats de cette théorie avec ceux des observations." Fourier, Mémoire de 1820
|
Autres thèmes développés dans les deux Mémoires de Fourier (1820, 1827)
Le Soleil, les Variations Saisonnières... et les Bonnes Caves
La question de la seule influence du rayonnement solaire est citée en premier par Fourier, dès 1820. Mais ce n'est pas le point qu'il veut développer dans ce mémoire, conformément au titre choisi. Il se contente donc d'énoncer le résultat, sans l'accompagner de justifications mathématiques, contrairement à l'effet de refroidissement.| "L'action des rayons du Soleil pénètre le globe, et cause des variations diurnes et annuelles dans les températures. Ces changements périodiques cessent d'être sensibles à quelque distance de la surface. Au delà d'une certaine profondeur, et jusqu'aux plus grandes distances accessibles, la température due à la seule influence du Soleil est devenue fixe; elle est la même pour les différents points d'une même verticale, et elle est égale à la valeur moyenne de la température." Fourier, Mémoire de 1820
|
Une belle illustration géographique en est fournie par la source de l'œil bleu,
au sud de l'Albanie, près de Saranda. Le mot source, consacré par
l'usage local, est en fait inexact: il s'agit d'une résurgence. L'eau a circulé sur 25km à 50m de profondeur ; sur une telle longueur, elle a eu tout le temps de se mettre à la température fixe (locale) de la profondeur -50m; aussi ressort elle (par une cheminée verticale) invariablement à 10°C, été comme hiver, alors que dans ce pays à la fois méditerranéen et montagneux, les contrastes saisonniers sont forts.
Cette "valeur moyenne de la température" est naturellement le premier terme, constant, du développement de Fourier de la température à la surface, qui est une fonction périodique, au moins en première approximation. Pour donner une idée peu plus précise, sans expliciter tous les nombres pour mieux saisir la forme, on aurait avec F périodique sue un an et paire
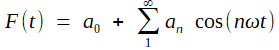
où ω = 2π / T, T étant la période. Ainsi, si t est exprimé en mois pour l'étude de la vatiation annuelle, ω = 2π / 12 = π / 6.
En ce cas, la solution sera, en fonction du temps t et de la profondeur x, de la forme (on verrra pourquoi un peu plus loin)
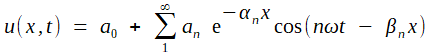
Les αn forment une suite positive, croissante; il est donc clair qu'à partir d'une certaine profondeur x, les exponentielles rendront négligeables tous les termes, et la température à partir de cette profondeur sera a0: c'est très exactement l'annonce de Fourier.
La forme des solutions peut vous étonner, en la comparant à celles que nous avons rencontré en parcourant la Théorie Analytique. Mais c'est tout simplement que l'on se trouve ici face à un problème d'un type différent de ceux que nous avions rencontrés jusqu'ici. Bien sûr, l'équation de la chaleur s'écrit toujours de la même manière; la différence vient des conditions complémentaires auxquelles est assujettie sa solution.
Ce travail est clairement présent dès le mémoire de 1811 (chapitre XII), comme l'atteste sa page 170 (que nous avons partagé en deux pour une meilleure visbilité, mais en respectant son pli: la liasse complète du mémoire est repliée en deux pour le stockage)
On l'a complété d'une deuxième ligne proposant pour cette température un modèle simple, à un seul terme oscillant. t est compté en mois, avec origine en juillet
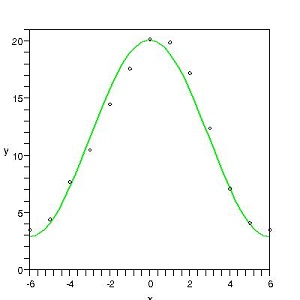
k a été évalué à environ 1,2 x 10-6 m²/s pour les matériaux de la croute terrestre par Kelvin ; dans les unités correspondantes ω est voisin de 2 x 10-7 rad/s, d'où une distance d = 3,5m. Le tableau et les graphiques qui suivent donnent les variations de température aux profondeurs d (en rouge) et 2d (en bleu), où l'excellence de la régulation peut être constatée. Aurait-on compliqué F d'un terme supplémentaire, cet ajout ne se ferait plus guère sentir à cette profondeur! On note enfin la possibilité de déterminer une profondeur qui rend la cave la plus fraîche au moment où il fait le plus chaud dehors: il suffit pour cela que le déphasage x/d vaille π; on a représenté cette courbe en brun. À cette profondeur, la température varie de moins de 1°C!
Que l'on soit atrrivé à une température quasi constante dans ce dernier cas n'a rien de surpremant: l'amplitude A de l'oscillation en surface (A = 8,6 dans notre exemple) a été divisée par exp(π), soit près de 25. Le résultat ne serait pas différent à Nice... car A y garde une valeur proche de 8; ce qui change, c'est la moyenne annuelle, qui passera à 16°C. Inutile de creuser plus profond, mais votre cave sera moins fraîche!
Enfin, si vous souhaitez calculer la moindre profondeur en fonction de l'amplitude δ des variations annuelles que vous êtes prêt à tolérer, il vous suffira de résoudre l'équation en x
| |
||
| La "source" bouillonne |
À la verticale de "l'œil"... ou presque (belvédère) |
La vigoureuse eau turquoise se calme en s'écoulant dans les bosquets |
Cette "valeur moyenne de la température" est naturellement le premier terme, constant, du développement de Fourier de la température à la surface, qui est une fonction périodique, au moins en première approximation. Pour donner une idée peu plus précise, sans expliciter tous les nombres pour mieux saisir la forme, on aurait avec F périodique sue un an et paire
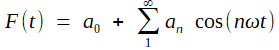
où ω = 2π / T, T étant la période. Ainsi, si t est exprimé en mois pour l'étude de la vatiation annuelle, ω = 2π / 12 = π / 6.
En ce cas, la solution sera, en fonction du temps t et de la profondeur x, de la forme (on verrra pourquoi un peu plus loin)
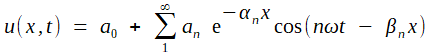
Les αn forment une suite positive, croissante; il est donc clair qu'à partir d'une certaine profondeur x, les exponentielles rendront négligeables tous les termes, et la température à partir de cette profondeur sera a0: c'est très exactement l'annonce de Fourier.
La forme des solutions peut vous étonner, en la comparant à celles que nous avons rencontré en parcourant la Théorie Analytique. Mais c'est tout simplement que l'on se trouve ici face à un problème d'un type différent de ceux que nous avions rencontrés jusqu'ici. Bien sûr, l'équation de la chaleur s'écrit toujours de la même manière; la différence vient des conditions complémentaires auxquelles est assujettie sa solution.
- Dans l'étude du refroidissement d'un solide, la donnée intiale est une fonction de x au temps t = 0 ;
- dans ce qui nous occupe, c'est une donnée au bord: une fonction du temps t à la profondeur x = 0 .
Ce travail est clairement présent dès le mémoire de 1811 (chapitre XII), comme l'atteste sa page 170 (que nous avons partagé en deux pour une meilleure visbilité, mais en respectant son pli: la liasse complète du mémoire est repliée en deux pour le stockage)
 |
 |
| Mémoire de 1811, p.170 (haut) : | Mémoire de 1811, p.170 (bas) : la traduction au bord (flèche bleue), qui revient à un développement de φ ,
le calcul de ses coefficients (flèche violette) |
Un Exemple Concret: pour une Bonne Cave... à Auxerre!
Si vous avez visité des grottes, des caves de vignerons, on vous aura immanquablement dit quelque chose comme : "La température n'y varie pratiquement pas au long de l'année, et vaut...". Non sans ajouter, dans le second cas, que c'est idéal pour la conservation des précieux liquides, ce dont on ne se permettra pas de douter. Voyons donc comment cela se traduit avec une localisation qui ne doit rien au hasard: ce serait faire injure à Fourier, au sol qui l'a vu naître et à la vigne qu'on y cultive de faira ailleurs que dans sa ville natale notre simulation numérique. On peut trouver sans peine, sur la page Wikipedia relative à Auxerre, un tableau des moyennes mensuelles des températures, ainsi que la moyenne annuelle : 11,5°C.On l'a complété d'une deuxième ligne proposant pour cette température un modèle simple, à un seul terme oscillant. t est compté en mois, avec origine en juillet
F(t) = 11,5 + 8,6 cos ( πt / 6 ) = 11,5 + 8,6 cos ωt
| Mois |
Jan |
Fev |
Mars |
Avr |
Mai |
Juin |
Juil |
Août |
Sept |
Oct | Nov |
Déc |
| tmoy (relevée) |
3,5 | 4,4 |
7,7 |
10,5 |
14,5 | 17,6 |
20,2 |
19,9 |
17,2 |
12,4 | 7,1 | 4,1 |
| tmod (modèle) |
2,9 |
4,1 | 7,2 | 11,5 | 15,8 | 18,9 |
20,1 | 18,9 | 15,8 | 11,5 | 7,2 | 4,1 |
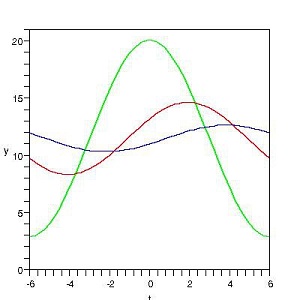
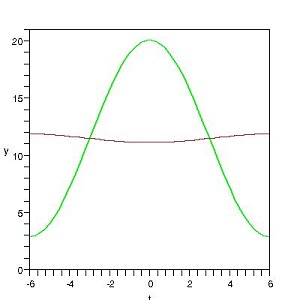
k a été évalué à environ 1,2 x 10-6 m²/s pour les matériaux de la croute terrestre par Kelvin ; dans les unités correspondantes ω est voisin de 2 x 10-7 rad/s, d'où une distance d = 3,5m. Le tableau et les graphiques qui suivent donnent les variations de température aux profondeurs d (en rouge) et 2d (en bleu), où l'excellence de la régulation peut être constatée. Aurait-on compliqué F d'un terme supplémentaire, cet ajout ne se ferait plus guère sentir à cette profondeur! On note enfin la possibilité de déterminer une profondeur qui rend la cave la plus fraîche au moment où il fait le plus chaud dehors: il suffit pour cela que le déphasage x/d vaille π; on a représenté cette courbe en brun. À cette profondeur, la température varie de moins de 1°C!
| Prof. approx. |
Mois |
Jan |
Fev |
Mars |
Avr |
Mai |
Juin |
Juil |
Août |
Sept |
Oct | Nov |
Déc |
| 0m |
u (0,t) (modèle) |
2,9 |
4,1 | 7,2 | 11,5 | 15,8 | 18,9 |
20,1 | 18,9 | 15,8 | 11,5 | 7,2 | 4,1 |
| 3.5m | u (d,t) | 9,8 |
8,7 |
8,3 |
8,8 | 10,0 |
11,6 | 13,2 |
14,3 |
14,6 | 14,1 | 12,9 | 11,3 |
| 7m | u (2d,t) | 12,0 |
11,4 |
10,4 |
10,3 | 10,6 | 11,0 | 11,6 | 12,2 | 12,6 | 12,7 | 12,4 | 11,9 |
| 10m |
u (πd,t) | 11,9 | 11,8 | 11,7 | 11,5 | 11,3 | 11,2 | 11,1 | 11,2 | 11,3 | 11,5 | 11,7 | 11,8 |
 |
 |
| température aux profondeurs 0, d, 2d |
température aux profondeurs 0 et πd |
Que l'on soit atrrivé à une température quasi constante dans ce dernier cas n'a rien de surpremant: l'amplitude A de l'oscillation en surface (A = 8,6 dans notre exemple) a été divisée par exp(π), soit près de 25. Le résultat ne serait pas différent à Nice... car A y garde une valeur proche de 8; ce qui change, c'est la moyenne annuelle, qui passera à 16°C. Inutile de creuser plus profond, mais votre cave sera moins fraîche!
Enfin, si vous souhaitez calculer la moindre profondeur en fonction de l'amplitude δ des variations annuelles que vous êtes prêt à tolérer, il vous suffira de résoudre l'équation en x
Ae- x/d = δ
| Complément technique: trouver la formule générale Pour passer de l'expression de F, exprimée comme série, à celle de la solution u,
on ne fait que généraliser le calcul de l'exemple. Il vaudra mieux,
comme souvent, travailler avec une représentation complexe, qui
simplifie grandement le calcul. Soit donc F donnée par
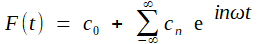 On cherchera la température à la profondeur x, toujours sous la forme d'un développement trigonométrique en t, mais dont les coefficients sont cette fois des fonctions de x: 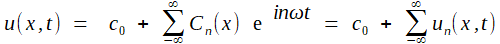 Sous réserve de pouvoir intervertir sommes et dérivations -ce qui est laissé au lecteur averti et consciencieux, il suffira que chaque un vérifie l'équation de la chaleur, ce qui revient à k C"n (x) = inω Cn (x) = ½ ( 1+ i)² nω Cn (x)
On y écrit i comme un carré, afin de préparer la forme classique de l'équation différentielle du second ordre y" = λ²y C"n (x) = (1+ i)² αn² Cn (x)
avec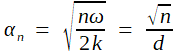 Cn (x) = An exp [-(1+ i) αn x] + Bn exp [(1+ i) αn x]
sauf qu'une exponentielle croissante n'a aucune pertinence dans ce contexte (Fourier nous l'a déja dit dans la Théorie Analytique) un (x,t) = An exp [-(1+ i) αn x + inωt]
= An e- αn x ei ( αn x - nωt ) ce qui est bien la forme annoncée. |
La Température de l'Espace
Curieuse et cruelle ironie du sort, on n'a souvent retenu, de ces remarquables mémoires, que la seule erreur qu'ils contiennent: une très mauvaise évaluation de la température de l'espace interstellaire..| "Notre
système solaire est placé dans une région de l'univers dont tous les
points ont une température commune et constante, déterminée par les rayons de lumière et de
chaleur qu'envoient tous les astres environnants. Cette température
froide du ciel planétaire est peu inférieure à celle des régions polaires du globe terrestre." Fourier, Mémoire de 1827
|
Ce qui procède d'un souci, au demeurant légitime, d'équilibre thermique entre la terre et son milieu environnement: il pense que sinon, la terre perdrait beaucoup trop de sa chaleur et ne pourrait maintenir à sa surface les températures qu'on y relève. Mais il sous-estime grandement, à ce moment précis, le rôle de couche isolante que constitue l'atmosphère, et sur lequel il va revenir avec la plus grande pertinence quelques pages plus loin.
| L'estimation
de Fourier revient à adopter pour l'espace une température entre -50°C
et-60°C, les plus basses mesurées (en Sibérie). Le premier
contradicteur sera le physicien Claude Pouillet (1790-1868), qui l'encadrera entre -115°C et-175°C, proposant, "d'après ses expériences", la valeur -142°C. Il se réclame de Fourier pour la théorie et lui rend hommage, avant de l'opposer à un Poisson qui a des vues plutôt déroutantes:
|
 |
||
| Buste de Pouillet, à l'ENS Ulm | Son mémoire (1838), consultable siur Gallica BnF |
Un homme dont le génie est toujours à l'affut de l'actualité va graver dans le marbre, ou du moins dans un de ses romans, l'erreur de Fouirer: Jules Verne! En 2019, pour les 150 ans de sa prmeière publication... et les 50 ans des premiers pas de Neil Armstrong et Buzz Aldrin sur la lune, ont été réédités à la fois un fac-simile de l'édition Hetzel et même le manuscrit original
En fait, ils se trompent tous les deux: nous savons aujourd'hui que cette température est encore bien plus basse, proche de -270°C, soit 3°C au dessus du zéro absolu: c'est celle du rayonnement fossile de l'Univers, signature du Big Bang. Une valeur à peu près inimaginable à l'époque des deux savants... Il faudra attendre le début du XXème siècle pour approcher vraiment le zéro absolu au laboratoire ( le Mathouriste ne résite pas au plaisir de vous faire voir le lieu et le héros de l'aventure) et le 20 mai1964 pour la découverte indiscutable du rayonnement fossile, conjecturé depuis 1948, par les physiciens américains Arno Penzias et Robert Woodrow Wilson. La difficulté du sujet offre donc quelques excuses aux malheureuses estimations de Fourier et Pouillet!
Les Réflexions sur l'Effet de Serre
C'est encore Pouillet qui, dans le même Mémoire, rend justice au rôle pionnier de Fourier en ce domaine.|
"M. Fourier
est, je crois, le premier qui ait eu l'idée de regarder l'inégale
absoption de l'atmosphère comme devant exercer une influence sur les
températures du sol. Il y avait été conduit par les belles
expériences faites par M. de Saussure, en 1774, sur quelques cimes
élevées des Alpes et dans les plaines voisines, pour comparer les
intensités de la chaleur solaire . [...]"
C. Pouillet, Mémoire sur la Chaleur Solaire, etc..(1838)
|
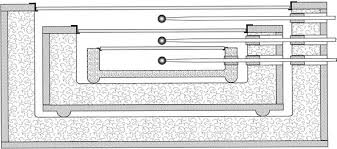 |
Fourier décrit avec précision le dispositif, dénommé héliothermomètre
par de Saussure; en fait de "vase", il s'agit plutôt
d'une caisse à trois vitrages superposés , la température étant relevée
dans chaque compartiment défini par les lames de verre et le fond
absorbant.Aucun appareil appartenant au savant n'a été conservé, le schéma ci-contre, issu de cet article sur l'histoire de l'effet de serre, est une reconstitution d'après la description de son inventeur. Précision utile: l'échelle de température octogésimale est celle de Réaumur, pour laquelle le point d'ébullition de l'eau est 80°, correspondant à 100°C.
|
||
|
 billet de 20 Francs Suisses à l' effigie de Saussure
au verso, reprise d'une gravure montrant son expédition au Mont Blanc,
un an après la première de Pacquard et Balmat. Son but est d'effectuer
diverses expériences en altitude, nortamment prouver que les
températures dans l'héliothermomètre ne dépendent pas de la température extérieure, qui s'abaisse avec l'altitude. |
||
 |
|||
Rendons à chacun son mérite: à De Saussure, l'envie de'expliquer l'échauffement à travers les vitres (d'où la multiplication des couches dans l'appareil de son invention), à Fourier l'idée géniale du rôle comparable de l'atmosphère. Mais il faut en préalable mieux comprendre le phénomène, et Fourier le résume ainsi:
| "La
théorie de cet instrument est facile à concevoir. Il suffit de
remarquer: 1° que la chaleur acquise se concentre, parce qu'elle n'est
point
dissipée immédiatement par le renouvellement de l'air; 2° que la
chaleur émanée du Soleil a des propriétés différentes de celles de la
chaleur
obscure. Les rayons de cet astre se transmettent en assez grande
partie au delà des verres dans toutes les capacités et jusqu'au fond de
la boîte. Ils échauffent l'air et les parois qui le contiennent : alors
leur chaleur ainsi communiquée cesse d'être lumineuse; elle ne conserve
que les propriétés communes de la chaleur rayonnante obscure." Fourier, Mémoire de 1827
|
Qu'est-ce donc que cette chaleur obscure? Ce que l'on n'appelle pas encore, au temps de Fourier, rayonnement infrarouge. Il est découvert en 1800 par l'astronome Willima Herschel, qui cherchait à mesurer les températures des rayons de différentes couleurs séparés par un prisme, à partir d'une lumière blanche, et constata l'élévation de la température dans la zone d'ombre proche de la partie rouge. L'absence de lumière visible associée vient expliquer cette dénomination historique. Quant au matériel expérimental, le Mathouriste a pu le voir dans la maison de William Herschel, à Bath. C'est aujourd'hui un beau petit musée dont il vous recommande la visite!
 |
 |
 |
|
| William Herechel, le prisme davec lequel il découvrit la "chaleur obscure", sa maison-musée à Bath (Angleterre) |
|||
Le pas supplémentaire que fait Fourier est de comprendre que l'atmosphère joue partiellement, pour la terre, le rôle du vitrage:
| "L'interposition de
l'air modifie beaucoup les effets de la chaleur à la surface du globe. Les
rayons du Soleil, traversant les couches atmosphériques condensées par
leur propre poids, les échauffent très inégalement[...]. La chaleur du
Soleil, arrivant à l'état de lumière, possède la propriété de pénétrer
les substances solides ou liquides diaphanes, et la perd presque
entièrement lorsqu'elle s'est convertie, par sa communication aux corps
terrestres, en chaleur rayonnante obscure. Cette
distinction de la chaleur lumineuse et de la chaleur obscure explique
l'élévation de température causée par les corps transparents La masse des eaux qui couvrent une grande partie du, tout en rendant hommahge globe et les glaces
polaires opposent moins d'obstacles à la chaleur lumineuse affluente
qu'à la chaleur obscure, qui retourne en sens contraire dans l'espace
extérieur. La présence de l'atmosphère produit un effet du même genre,
mais qui, dans l'état actuel de la théorie et à raison du manque
d'observations comparées, ne peut encore être exactement défini." Fourier, Mémoire de 1827
|
Dit de façon un peu plus moderne: l'énergie reçue du rayonnement solaire par la terre est partiellement réémise (conformément à la thermodynamique, vers l'atmosphère plus froide) sous forme de rayonnement infrarouge. Lequel peut être y retenu par les gaz qui y sont présents et possèdent une grande capacité d'absorption dans la partie infrarouge: ils retiendront et réémétront cette chaleur vers la terre, apportant ainsi un supplément calorique. Ce sont les désormais (malheiureusement) célèbres gaz à effet de serre, que recense déjà le chimiste suédois Svante Arrhenius (1859-1927, prix Nobel 1903), tout en rendant hommage à ses prédécesseurs, et, au tout premier rang, à Fourier:
Il mérite qu'on le cite un peu plus largement ici, tant sa pensée apparaît comme le meilleur prolongement de celle de Fourier. La vapeur d'eau et le gaz carbonique sont les principaux responsables: en un sens, c'est heureux, car sinon la terre serait beaucoup plus froide... donc moins habitable! Arrhenius évalue (à lui tout seul, bien avant qu'une cohorte d'experts du GIEC s'attèle, avec plus de précision sans doute, à la même tâche) les effets de la quantité de CO2 (alors nommée acide carbonique) rejetée
|
"
La disparition de la moitié de l'acide carbonique existant causerait un
refroidissement d'environ 4 degrés; la diminution jusqu'au quart de la
proportion actuelle nous ferait perdre 8 degrés. L'acide carbonique doublerait-il en quantité, que nous y gagnerions 4 degrés; il devrait augmenter de quatre fois son volume actuel pour gagner 8 degrés.
S. Arrhenius, L'Évolution des Mondes (1907)
|
Sa conclusion est remarquable pour l'époque: il a compris la fragilité de l'équilbre naturel, qui n'a rien d'acquis de toute éternité (on sort tout juste du petit âge glaciaire, qu'il commente longuement), et le risque d'aller vers un dérèglement climatique. Il pointe avec un siècle d'avance une gestion des ressources insouciante de l'avenir et les dangers d'une démographie galopante. Sa conclusion -il veut croire en un monde meilleur-peut certes sembler naïve, du moins exagérément optimiste aujourd'hui, d'autant qu'elle ne prend pas en compte l'effet d'une désertification dans les pays du Sud; mais à le replacer dans son époque, on salueara la pertinence de ses idées générales.
|
"
On entend souvent exprimer des craintes parce que les réserves de
houille existant sur notre globe sont attaquées et consommées par la
civilisation actuelle, sans qu'on ait aucune prévoyance ni égards pour l'avenir.
On s'effraie en même temps des énormes pertes de vies et de biens qui
sont la conséquence des phénomènes volcaniques de nos jours. Peut-être
trouvera-t-on qu'il convient de se rassénérer en se rappelant qu'il n'y
a ici, comme souvent, qu'un dommage d'un côté pour un bien de l'autre.
Par suite de l'augmentation de l'acide carbonique dans l'air, il nous
est permis d'espérer des périodes qui offriront au genre humain des
températures plus égales et des conditions climatiques plus douces.
Cela se réalisera sans doute dans les régions les plus froides de la
terre. Ces périodes permettront au sol de produire des récoltes
considérablement plus fortes qu'aujourd'hui, pour le bien d'une population qui semble en voie d'accroissement plus rapide que jamais [...]"
S. Arrhenius, L'Évolution des Mondes (1907)
|
Or, rien de tout cela n'avait pas échappé à Fourier, un siècle avant exactement (si l'on prend pour référence le dépôt de son premier mémoire à l'Académie), et c'est d'autant plus méritoire que, dans son cas, la révolution industrielle était encore à venir! Sans oublier, lui non plus, les aleas naturels, li mentionnait deux fois la contribution anthropique dans le Mémoire de 1827, à près de dix pages d'écart. Il ne faisait que reprendre une idée non moins clairement exprimée dans celui de 1820.
| Fourier, Mémoire de 1827 | Fourier, Mémoire de 1820 |
"Les mouvements de l'air et des eaux, l'étendue des mers, l'élévation et la forme du sol, les effets de l'industrie humaine et tous les changements accidentels de la surface terrestre modifient les températures dans chaque climat. Les caractères des phénomènes dus aux causes générales subsistent; mais les effets thermométriques observés à la superficie sont différents de ceux qui auraient lieu sans l'influence des causes accessoires.
[...]
L'établissement et le progrès des sociétés humaines, l'action des forces naturelles peuvent changer notablement, et dans de vastes contrées, l'état de la surface du sol; la distribution des eaux et les grands mouvements de l'air. De tels effets sont propres à faire varier, dans le cours de plusieurs siècles, le degré de la chaleur moyenne; car les expressions analytiques comprennent des coefficients qui se rapportent a l'état superficiel et qui influent beaucoup sur la valeur de la température." |
"D'autres causes accessoires, propres à chaque climat, ont une influence bien plus sensible sur la valeur moyenne des températures à l'extrême surface. L'expression analytique de cette valeur moyenne contient un coefficient numérique qui désigne la facilité avec laquelle la chaleur des corps abandonne la dernière surface et se dissipe dans l'air. Or cet état de la superficie peut subir, par les travaux des hommes, ou par la seule action de la nature, des altérations accidentelles qui s'étendent à de vastes territoires: ces causes influent progressivement sur la température moyenne des climats. On ne peut douter que les résultats n'en soient sensibles, tandis que l'effet de refroidissement du globe est devenu inappréciable." |
 |
En outre, il raisonne en climatologue, envisageant le globe dans son ensemble, plutôt que les seuls risques d'altération locale qui apparaîtront comme
évidents dès la seconde moitié du XIXème siècle (régions sidérurgiques,
fog londonien...). La transposition de l'expérience de Saussure à
l'atmosphère aurait fort bien pu être envisagée dans une zone limitée;
cette globalisation des phénomènes n'allait nullement de soi. Deux
influences ont pu l'y inciter: la connaissance des travaux d'Alexander von Humboldt,
qu'il cite explicitement en 1827 (ce très francophile Allemand était
installé à Paris, associé étranger de l'Académie depuis 1810) et la
mémoire de l'éruption du Laki en 1783 (évoquée dans notre page sur Bézout), génératrice d'un long désordre atmosphérique mondial. Ce qui justifie d'avoir placé l'action des forces naturelles à côté de celle des sociétés humaines.
|
| Statue d'Alexander von Humboldt devant l'université Humboldt de Berlin.
Elle est ainsi nommée en l'honneur des deux frères: Wilhelm, linguiste,
a sa statue à gauche de l'entrée, placée symétriquement par rapport
au portail d'entrée. |
C'est un beau et fort symbole de voir qu'aujourd'hui, que ce soit depuis la terre ou des stellites (la sonde Cassini par exemple), la télésurveillance des gaz à effet de serre dans l'atmosphère repose sur la spectroscopie infrarouge par transformation de Fourier (à découvrir en détails dans notrre page sur les applications en spectroscopie). La transformation rapide, bien entendu, sinon nos meilleurs ordinateurs seraient submergés sous le volume des calculs...
Conclure
Fourier a compris et entrevu, avant tout le monde.Et nous ne sommes pas les seuls à le dire; regardez la présentation à la presse des Prix Nobel de Physique 2021: pour introduire les travaux de Syukuro Manabe et Klaus Hasselmann (récipiendaires chacun d'un quart du prix), John Wettlaufer, membre du Comité Nobel pour la Physique, revient à... Fourier!
Syukuro Manabe a construit, en 1967, le premier modèle global du climat prenant en compte l'effet de serre et la convection; il est considéré comme un pionnier du traitement informatique du problème. 10 ans plus tard Klaus Hasselmann expliquait pourquoi l'on peut prédire l'évolution du climat malgré le caractère chaotique de la météorologie ( il nous paraît important de rappeler ici que la découverte du chaos météorologique par Lorenz repose sur l'utilisation de développements de Fourier, voir notre page).
Au fait, le savez-vous? Certains d'entre vous, chers lecteurs, voient chaque jour un écho artistique du modèle de Manabe... dans la station RER de la gare du Nord! L'artiste britannique Liam Gillick a "décoré" les murs de béton, à la demande de la SNCF, en s'inspirant librement des formules de son article; ce qui compte pour lui est l'esthétique des caractères mathématiques, et non leur sens; il réagit au texte comme nous pouvons être sensibles aux textes en langue arabe (si nous ignorons tout de la langue) qui décorent les murs des mosquées.
Fourier nous a aussi fourni les mathématiques de notre outillage de détection; et si bien sûr, il ne pouvait s'en douter, il ne cessait de réaffirmer le caractère pérenne d'une théorie qui appartiendrait pour toujours aux sciences mathématiques. La jeunesse et l'efficacité de la spectroscopie par transformée de Fourier montrent que cette confiance en son œuvre n'était en rien trop orgueilleuse.
Mais Fourier ne peut pas tout pour nous, à notre place de citoyens du monde. Nous avons trouvé un sage pour dire, mieux que nous ne le ferions, ce qu'il laisse à notre responsabilité collective. On s'inquiètera légitimement de ce que ce discours fut prononcé 30 ans avant que cette page ne soit écrite, qu'il ne sera pas difficile de décomposer en septennats et quinquennats.
|
"Mais dans quel temps, derechef, vivons-nous, même quand il se réduit
à celui qui passe et coule ? Réponse aujourd'hui universelle
: dans le très court terme. Pour sauvegarder la terre ou respecter
le temps, au sens de la pluie et du vent, il faut vivre et penser dans le
très long terme, et, pour n'y vivre pas, nous avons désappris
à penser selon ses rythmes et sa portée. Soucieux de se maintenir,
le politique forme des projets qui dépassent rarement les élections
prochaines, sur l'année fiscale ou budgétaire règne
l'administrateur et au jour la semaine se diffusent les nouvelles des
médias ; quant à la science contemporaine, elle naît
dans des articles de revues qui ne remontent presque jamais en-deçà
de dix ans ; même si les travaux portant sur le paléo-climat
comptent par dizaines de millénaires, ils ne datent pas eux-mêmes
de trois décennies. Tout se passe comme si les trois pouvoirs
contemporains ici réunis, j'entends par pouvoirs les instances qui,
nulle part, ne rencontrent de contre-pouvoirs, avaient éradiqué
la mémoire du long terme, les traditions millénaires, les
expériences accumulées par les cultures qui viennent de
mourir.
Or nous voici en face d'un problème causé par une civilisation en place depuis maintenant plus d'un siècle, elle-même engendrée par les cultures longues qui la précédèrent, face à des dommages causés sur un système physique âgé de millions d'années, relativement stable par variations rapides, aléatoires et multiséculaires, devant une question angoissante dont la composante principale est le temps et spécialement celui du très long terme ; notre contradiction majeure consiste à lui proposer des réponses et des solutions de très court terme, parce que nous ne vivons qu'à échéances immédiates et que de celles-ci nous tirons l'essentiel de notre pouvoir. Les administrateurs tiennent la continuité, les médias la quotidienneté, la science enfin le seul projet d'avenir qui nous reste. Les trois pouvoirs détiennent le temps, au premier sens, pour maintenant statuer sur le second. Certes, nous pouvons ralentir les processus déjà lancés, légiférer pour consommer moins de combustibles fossiles, replanter en masse les forêts dévastées... toutes excellentes initiatives, mais qui se ramènent, au total, à la figure du vaisseau courant à vingt-cinq noeuds vers une barre rocheuse où immanquablement il se fracassera et sur la passerelle duquel l'officier de quart commande à la machine de réduire la vitesse d'un dixième sans changer de direction. D'un problème de long terme, la solution, pour devenir efficace, doit égaler la portée. Ceux qui vivaient dehors et dans le temps de la pluie et du vent, induisant par leurs gestes des cultures longues, les paysans et les marins, n'ont depuis longtemps plus la parole ; elle nous reste, à nous, administrateurs, journalistes et savants, tous hommes de court terme, en partie responsables des dommages infligés au temps, pour avoir inventé ou propagé les moyens et les outils d'interventions puissantes et dommageables, inhabiles à trouver des solutions raisonnables parce qu'immergés dans le temps bref de nos pouvoirs. Il existe une pollution matérielle, certes, technique et industrielle, qui met en danger le temps, au sens de la pluie et du vent, mais il en existe une deuxième, invisible, qui met en danger le temps qui passe et coule, pollution culturelle que nous avons fait subir aux pensées longues, ces gardiennes de la terre, des hommes et des choses elles-mêmes. Sans lutter contre la seconde, nous échouerons dans le combat contre la première. Nul ne peut réussir dans une entreprise de long terme avec des moyens de terme court : il nous faut payer un tel projet par une révision déchirante de la culture induite aujourd'hui par nos trois pouvoirs." |
Références
- G.L. BUFFON , Histoire Naturelle, Introduction à l'Étude des Linéraux. Supplément, tome 1. (en ligne sur Gallica BnF)
- A.S. EVE, Rutherford (Cambridge University Press 1939, en ligne sur Gallica BnF)
- T. KÖRNER, Fourier Analysis (Cambridge University Press)
- E. RUTHERFORD, F. SODDY, Radioactive Change in Philosophical Magazine (1903); [commentaire détaillé sur BibNum]
- W. THOMSON (Lord KELVIN), P. TAIT, Traité de Philosophie Naturelle, vol.I, part.II, édition de 1883 (Cambridge University Press)
À propos du Climat et de l'Effet de Serre, où l'on cite Fourier
- S. ARRHENIUS, L'Évolution des Mondes (1907)
- T.R. ANDERSON, E. HAWKINS, P.D.JONES, CO2, the Greenhouse Effect and Global Warming: from the Pioneering Work
of Arrhenius and Callendar to Today's Earth System Models (Endeavour, 2016)
- E. BARD, Effet de serre et glaciations, une perspective historique (Collège de France, 2004)
- G. BORVON, Une brève histoire de l'effet de serre et du changement climatique (2018)
- J.-L. DUFRESNES, Jean-Baptiste Joseph Fourier et la Découverte de l'Effet de Serre (La Météorologie n°53, 2006)
- R.T. PIERREHUMBERT, Warming the World (Nature, 2004)
Oeuvres de Fourier disponibles en téléchargement sur le site de la B.N.F.
- Théorie Analytique de la Chaleur (édition de 1822)
- Œuvres de Fourier, tome2: Mémoires publiés dans divers recueils (publiés par Gaston Darboux), dont les deux étudiés ici:
- Extrait d'un Mémoire sur le Refroidissement Séculaire du Globe Terrestre (Mémoire de 1820)
- Mémoire sur les Températures du Globe Terrestre et des Espaces Planétaires (Mémoire de 1827)
Et aussi...
- Joseph Fourier et la préhistoire de l’effet de serre : une conférence de Raymond Pierrehumbert (univ. de Chicago), en vidéo, sur le site Diffusion des Savoirs de l'École Normale Supérieure.
- La théorie de la chaleur de Fourier appliquée à la température de la Terre: article de James Lequeux sur le site BibNum
- Changement climatique : prévision, scénario, catastrophisme, une conférence d'Hervé Le Treut (Académie des Sciences & École Polyrechnique)
- Wikipedia : le Changement Climatique
- Wikipedia : Histoire de la Recherche sur le Changement Climatique (beaucoup plus complète en Anglais, ou en Allemand)
Poursuivre dans le Monde de Fourier...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique