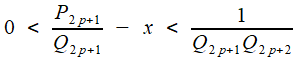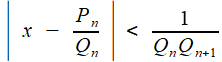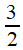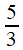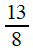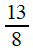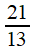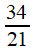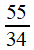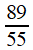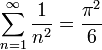Fractions
Continuées,
une
Promenade Initiatique

|
Écoutons
(ci-contre) la parole d'un expert (ci-dessous)

Lagrange,
à l'ENS Ulm
|
|
Et
posons nous la question:
la
situation a-t-elle vraiment changé?
|
Elles
sont pourtant l'outil
le plus simple et le plus naturel des démonstrations
d'irrationnalité,
la source d'approximations numériques parmi les plus
performantes, tout en restant mal aimées et tenues à
l'écart des programmes d'enseignement.
La Racine et la Divine: Pythagore et Pacioli
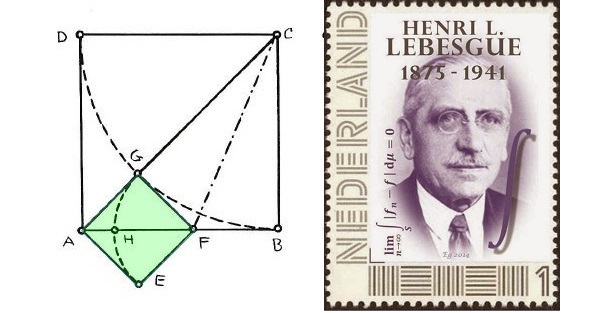
Voici
l’introduction que propose Henri Lebesgue dans ses Leçons
sur les Constructions Géométriques (1941).
Il
considère pour cela la question du rapport x
de la diagonale du carré à son côté. Il trace un arc de cercle centré en C, dont le rayon est le côté, et qui coupe la diagonale en G. Alors
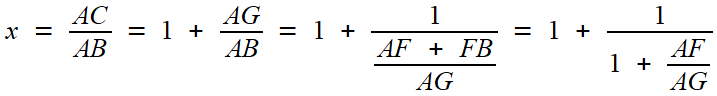
car AF = GF = BG
ce qui se traduit par l'équation en x -qui n'est, au premier stade, qu'une manière un peu tordue de réécrire...
x² = 2
|
|
|
Mais "l'originalité" est ici de reporter cette égalité dans le x
du dénominateur, ce qui rajoute un étage ( en sous-sol!) à la
fraction. Et il n'y a aucune raison de ne pas réitérer! Notez quà
chaque étape, c'est toujours l'équation x² = 2 que
l'on écrit, d'une façon de plus en plus alambiquée. Ce qui suggère
d'écrire, puisque cette substitution peut être réalisée indéfiniment:

La terminologie fraction continuée s'impose naturellement (et le
processus apparait comme "cousin" de la réitération du + pour les
séries, du × pour les produits infinis). Néanmoins, suggérer n'est pas prouver! D'autant qu'il faut donner un sens, comme limite, à ces points de suspension.
Prouver dans ce cas, c'est facile! (mais on peut sauter sans inconvénient si l'on n'a pas envie...)
Prouver consistera à montrer que la suite dont le nième terme est la fraction finie "à n traits de division
superposés" converge vers la limite attendue (on met provisoirement de
côté la partie entière 1, pour exploiter une parfaite régularité)

Or ces termes vérifient l'équation de récurrence
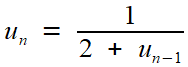
que l'on peut étudier par la méthode élémentaire (les détails, faciles, sont laissés au lecteur) : sa limite vérifie
|
L'écriture du nombre "avec une infinité d'étages" diagnostiquera instantanément son irrationnalité,
comme on le verra un peu plus loin. On tient donc là une preuve, qui
plus est d'origine géométrique, de ce résultat qui avait tant perturbé
les pythagoriciens.
Le trop célèbre nombre d'or
est justiciable d'un traitement en tous points analogue. S'il est
effectivement trop célèbre par le nombre des délires
artisco-géométriques qu'il a suscités, il peut être considéré comme le
plus simple de tous les nombres sous l'angle de son développement en
fraction continuée!
 |
« Une droite est dite coupée en extrême et moyenne raison quand elle est tout entière relativement au plus grand segment, comme est le plus grand relativement au plus petit. »
Euclide, les Éléments, II.11
|
Cela revient à dire que le rapport (a+b) / a est égal au rapport a / b. Il en résulte immédiatement que x = est la racine positive de l'équation du second degré
x²
- x - 1 = 0
C'est bien plus tard (au début du XXème siècle) que sa racine positive sera notée Φ, en hommage à Phidias, vu comme l'architecte des proportions idéales. Elle est nommée Divine Proportion
par Luca Pacioli, qui en fait le sujet d'un traité publié en 1509, avec
de belles illustrations d'un certain... Leonardo Da Vinci.

|

|

|

|
Édition 1509, page-titre
(source: Wikipedia)
|
Luca Pacioli
(attribué à Jacopo de Barbieri, Musée de Naples)
|
Une gravure de Leonardo
|
à lire absolument...
... comme garde-fou!
|
On réécrit l'équation sous une forme propice à la réitération, et on reporte, exactement comme dans le cas précédent.
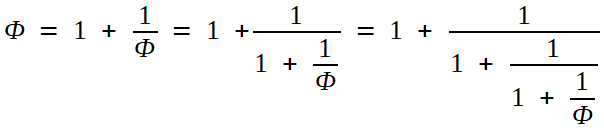
ce qui suggère la formule illimitée
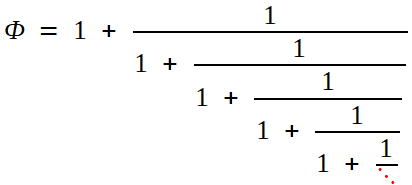
On peut la démontrer avec le même procédé élémentaire.
Des Racines et des "l"...
Peut-on aller plus loin, avec la racine carrée de 3, par exemple,
puis celle de 7, puis d'autres? Avec des racines cubiques?
Un peu plus compliqué, mais à peine: 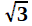
La forme à répétition 1/... suggère de préparer le travail en isolant la partie entière, puis en écrivant la partie fractionnaire
(donc, plus petite que 1) comme inverse d'un nombre plus grand que 1,
ce qui offre un espoir de réitération: on verra bientôt le caractère
"historique" de cette approche.
C'est un tout petit peu plus acrobatique, mais l'usage de la quantité conjuguée renvoie la racine en dénominateur:
Puis on s'arrange pour que la nouvelle fraction ait pour numérateur 1, selon le programme décidé, et l'on isole la partie entière (c'est de nouveau 1) pour recommencer
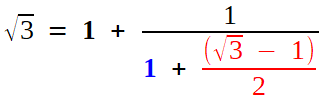
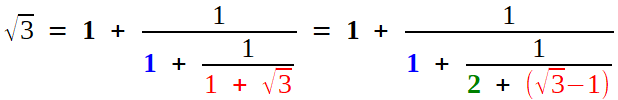
Tiens! Cette fois, la partie entière est 2. Mais surtout, on voit réapparaître  , dont on était parti. Volià, on peut réitérer, une fois d'abord, et, on espère, indéfiniment.
, dont on était parti. Volià, on peut réitérer, une fois d'abord, et, on espère, indéfiniment.
Et l'on peut adapter notre preuve élémentaire,
Mais il se peut que la racine 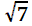 vous donne un peu plus de fil à retordre... nous la soumettrons un peu plus loin.
vous donne un peu plus de fil à retordre... nous la soumettrons un peu plus loin.
Le "premier" exemple historique: Bombelli et 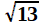
Il est toujours délicat de
parler de primauté: l'expérience montre souvent qu'il y avait un "plus
premier avant le premier", si l'on ose dire, et cette
première européenne ne fera pas exception. Bologne est à la
Renaissance, un centre important pour les mathématiques, et notre
pionnier est Rafaele Bombelli (1526-1572). L'année de son décès paraît
une première édition de son ouvrage d'Algèbre, probablement écrit 10 à
12 ans auparavant. Il y donne un développement à la fois similaire... et diffférent.
Diffférent, en ce sens: les numérateurs successifs des fractions (qu'on nommera désormais numérateurs partiels) ne sont plus des 1, mais des nombres quelconques, au même titre que les dénominateurs partiels.
Bombelli n'utilise pas la graphie ci-dessus, mais l'algorithme de
calcul d'une racine carrée qu'il propose, une fois dégagé de sa lourde
gangue de phrases, revient à cette formule.
On démarre en utilisant le plus petit carré inférieur au
nombre proposé: 13=3²+4. La suite est assez semblable aux cas
antérieurs, qu'on en juge!
Une fois de plus, on aura utilisé la quantité conjuguée pour faire réapparaître une quantité identique, et ainsi réitérer ad infintam.
Et une preuve élémentaire repose sur...
... l'étude de la suite récurrente 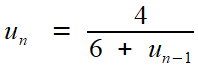 |
"Premier" exemple, pourquoi pas... mais faut-il créditer Bombelli? Découvert en 1881 à 80km de Peshawar (Pakistan), le manuscrit de Bakhshali contient le premier et le troisième approximants issus d'un développement similaire pour le calcul des racines carrées.

|
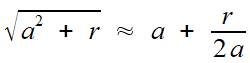
|
|
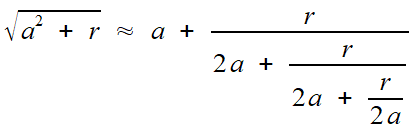
|
|
source de l'image: Bodleian Library, Oxford
|
|
Daté au carbone 14
en 2017, ce texte a été écrit entre 200 et 400 de notre ère -il a ainsi
défrayé la chronique, car il contient de nombreuses occurences du zéro,
plus de 400 ans avant la fameuse stèle indienne de Gwalior... Pour
notre affaire, il reste du mystère, car les approximations sont données
sous une forme littéraire, et surtout n'indiquent pas l'usage successif
de ces divisions: le premier approximant est connu un peu partout
depuis l'antiquité, le deuxième manque (ce qui se comprend mal, si l'on
a vu le caractère répétitif de la formule), et le troisième donné sous
une forme équivalente, certes, mais d'origine mystérieuse (une
compensation soustractive au premier)
Nos petits bricolages ayant clairement des limites, il est temps de
donner un procédé de recherche plus sytématique, qui nous aidera en
retour à trouver et démontrer le développement de 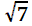
Huygens, le premier "développeur"
Jusqu'ici, nous avons exploité
des particularités liées à certains nombres pour deviner, puis prouver
leur développement. Un point commun se dégage clairement: l'utilsation d'une équation du second degré, ... mais laquelle? Pas la plus immédiate, qui serait x² - N = 0 pour approcher la racine carrée de N. Les tâtonnements ont vite montrés leurs limites, dès N = 7. La recherche d'une méthode systématique, d'abord pour le cas des fractions continuées régulières (c'est à dire, celles dont tous les numérateurs partiels sont des 1) s'impose. Voici ce qu'en dit Lagrange:

|
"La
première solution de ce Problème a été donnée par Wallis [...] ; mais
la méthode de cet Auteur est indirecte et fort laborieuse. Celle que
nous [allons] donner est dûe à Huyghens, et l'on doit la regarder comme
une des principales découvertes de ce grand Géométre. La construction de son automate planétaire paraît en avoir été l'occasion."
Lagrange, Additions aux Éléments d'Algèbre d'Euler (Œuvres, tome 7)
|

|

|
1703 pour la publication,
mais l'automate a été construit en 1682
|
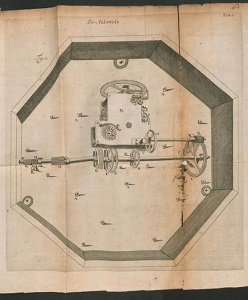
le fameux planétaire, au musée Borhaeve (Leiden, Pays Bas)
Les
vitres sont une plaie pour photographier l'objet, mais une excellente
idée est d'en avoir disposé une à l'arrière, qui permet de voir, en
dépit des reflets, tous les engrenages. Bref, nous vous conseillons
d'allet le découvrir sur place!
|
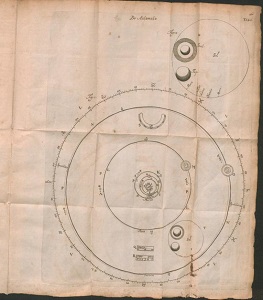
Il s'agit de fabriquer un
mécanisme d'horlogerie reproduisant fidèlement le mouvement des
planètes autour du soleil. La difficulté pratique en est évidente, et
Lagrange expose très clairement le problème d'approximation que posent
les deux limitations techniques: le nombre de dents par engrenage d'une
part, le nombre de roues dentées de la machine d'autre part.
 |
En effet, il est clair que pour pouvoir représenter exactement les mouvements des planètes, il faudrait employer des roues où les nombres des dents fussent précisément dans les mêmes rapports que les périodes
dont il s'agit; mais, comme on ne peut pas multiplier les dents au delà
d'une certaine limite dépendante de la grandeur de la roue, et que
d'ailleurs les périodes des planètes sont incommensurables ou du moins ne peuvent être représentées avec une certaine exactitude que par de très grands nombres, on est obligé de se contenter d'un à peu près, et la difficulté se réduit à trouver des rapports exprimés en plus petits nombres, qui approchent autant qu'il est possible de la vérité, et plus que ne pourraient le faire d'autres rapports quelconques qui ne seraient pas conçus en termes plus grands.
|
Huyghens résout cette question par le moyen des fractions continues [...]; il donne la manière de former ces fractions par des divisions continuelles,
et il démontre ensuite les principales propriétés des fractions
convergentes qui en résultent, sans même oublier les fractions
intermédiaires."
Lagrange, Additions aux Éléments d'Algèbre d'Euler (Œuvres, tome 7)
|
|
Suivons donc Huygens dans son travail: petit coup d'œil aux pages clés
avant de détailler le procédé, succession de divisions à partir d'une
valeur approchée très précise du quotient des angles parcourus lors
d'une année (terrienne!) par Saturne et la Terre (c'est donc un peu
moins de 360° pour cette dernière).

|

|

|
la première page;
elle commence par l'évocation d'une science millénaire
|
partir d'une bonne approximation rationnelle du rapport;
le développer par divisions successives...
|
... puis, tronquer le développement:
on obtient une fraction proche, mais "plus raisonnable"
|
Prenons, pour abréger le calcul, un rapport un peu moins précis, 777084 / 26409.
On effectue la division avec reste (division euclidienne) du numérateur par le dénominateur; le rapport donné s'écrit comme somme d'un entier
et d'une fraction inférieure à 1, par construction. Cette
dernière peut, du coup, s'écrire comme inverse d'une fraction, à
laquelle s'appliquera le même procédé. Ainsi se dessine un algorithme de calcul!
777084 = 29 × 26409 + 11223
|
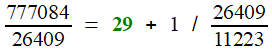
|
26409 = 2 × 11223 + 3963
|
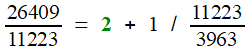
|
| 11223 = 2 × 3963 + 3297 |
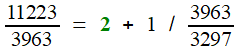
|
| 3963 = 1 × 3297 + 666 |
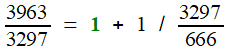
|
| 3297 = 4 × 666 + 33 |
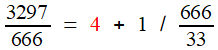
|
| 666 = 19 × 33 + 6 |
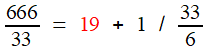 |
33 = 5 × 6 + 3
|
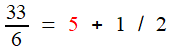
|
6 = 3 × 2 + 0
|
|
Un algorithme que nous reconnaissons, bien sûr! Ce n'est autre que le célèbre algorithme d'Euclide
(dont le dernier reste non nul est le PGCD du couple numérateur |
dénominateur ). Qu'il soit pratiqué depuis l'antiquité grecque explique
les nombreuses traces "archaïques" de fractions d'approximations
similaires à une réduite, c'est à dire la réduction à la forme p / q du développement tronqué à un certain stade, sans toutefois que la disposition "à la Huygens" n'apparaisse.
Mais revenons à Huygens: ces calculs successifs peuvent être "empilés" en une fraction continuée finie, et l'on a
On a noté en vert les dénominateurs partiels identiques à ceux obtenus par Huygens; ils diffèrent (en rouge) à partir d'un certain rang, parce que la fraction initiale n'est pas la même. Les réduites sont les fractions successives
dont on peut vérifier qu'elles s'approchent de plus en plus de la fraction de départ. On
s'est arrêté à la quatrième, car c'est l'approximation que choisit
Huygens pour son automate: il a calculé que l'erreur ainsi commise
n'excèdera pas 40' d'angle au cours d'un siècle!
Cette qualité d'approximation n'a rien de fortuit: on verra un
peu plus loin qu'elle est "congénitale" à l'algorithme des fractions
continuées.
Des Racines et des "l", #2...
Le cas 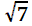
Appliquons à ce nombre rétif la méthode de Huygens, en le
remplaçant par une valeur décimale approchée. Et amorçons l'algorithme
d'Euclide:
C'est suffisant pour conjecturer la périodicité du développement, en répétant le motif 1, 1 , 1, 4 . C'est à dire écrire
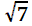
=
[ 2, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, ...]
en adoptant la convention limpide: remplacer la succession d'étagères (qui n'est certes pas sans charme...) par la liste des dénominateurs partiels.
Et maintenant qu'on tient notre suspect, il n'y a plus qu'à repartir en
sens inverse en partant du développement périodique suggéré, comme on
l'a fait pour 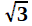
Prouver, c'est toujours facile!
pour montrer
|
étudier la récurrence
|
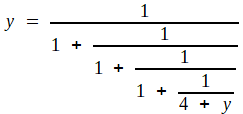
|
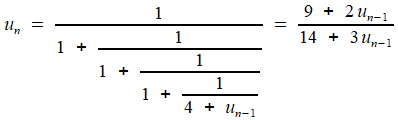
|
la limite positive vérifie ( y + 2)² = 7 ... et le tour est joué!
|
Deux Remarques
1. Le mécanisme précédent permet de trouver la limite de n'importe quel développement périodique (ou périodique à partir d'un certain rang). En réduisant la fraction qui exprime un en fonction de un-1 , on aura toujours une expression de la forme (dite homographique)
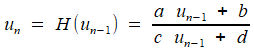 dont la limite vérifie
dont la limite vérifie
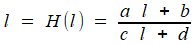
ce qui fait de l un nombre
quadratique, i.e. racine d'une équation du second degré. En fait, la
réciproque est vraie (mais nous ne la démontrons pas ici) : toute racine d'une équation du second degré a un développement périodique. C'est, du nom de son auteur, le
|
Théorème de
Lagrange : un nombre est quadratique si et seulement si son
développement en fraction continuée est périodique à partir dun certain
rang.
|
et il n'est pas peu fier d'avoir prouvé cette réciproque: voyez ce qu'il en dit dans son Traité de la Résolution des Équations Numériques (de tous les Degrés)
2. Pourquoi avons nous facilement traité les racines de 2,3,5 ... et pas 7?
Cela résulte du développement que nous avons évoqué à propos du manuscrit de Bakhshali (paragraphe dédié à 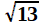 ), à savoir
), à savoir
si r = 1, on obtient immédiatement un développement régulier. Les racines de 2 et 5 sont dans ce cas, et en général
si r = 2, une simplification par 2 ramène encore à une fraction
régulière... mais attention à la façon d'opérer cette simplification!
En la suivant à la trace, on constate qu'elle ne concerne qu'un tour
sur deux. On retrouve le résultat de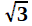
D'autres Racines? D'autres Nombres?
Se poser la question des racines cubiques est bien naturel.
Partant d'une bonne valeur décimale approchée, la méthode de Huygens
peut laisser espérer des découvertes, si ces nombres admettent des
développements dont les dénominateurs partiels obéissent à une loi
générale simple. Ainsi, par exemple
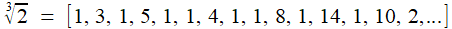
... Hélas, rien ne se révèle, et
du reste, rien n'est connu
à ce jour pour les racines cubiques, malgré la montée en puissance des
moyens de calculs qui permettent de pousser plus loin le développement.
Et π ? Grande question, bien sûr! C'est le premier exemple de nombre irrationnel que prend Lagrange dans ses Additions aux Éléments d'Algèbre d'Euler, invitant -cela mérite d'être souligné- à développer, non pas une fraction décimale d'approximation, mais deux qui encadrent le nombre proposé, afin de ne tenir pour sûrs que les dénominateurs partiels communs. Mise en pratique à partir de la valeur donnée par Viète, 3,14159 par défaut et 3,14160 par excès. La valeur plus précise à 35 décimales qu'il donne ensuite est l'occasion de rappeler qu'à l'époque, π ne s'appelle pas π, mais nombre de Lüdolph, du nom du recordman de l'époque(1596), Lüdolph Van Ceulen ("de Cologne"! 1540-1610) . Il faut dire que son record tiendra un peu plus de 100 ans...
 |
 |
Le fameux pilier de la cathédrale de Leiden (Pays Bas), au pied duquel Lüdolph est enterré, rappelle son exploit!
|
|

|
 |
Mais parfois, la méthode paye. Et la ténacité des grands calculateurs
est, dans cette chasse, récompensée comme celle des grands astronomes
dans la chasse aux étoiles et planètes: c'est ainsi qu'Euler découvre une loi remarquable pour les dénominateurs partiels du nombre e . Il n'aura plus qu'à repartir en sens inverse, comme nous l'avons modestement fait abvec 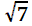 , pour démontrer. En deux lignes, il élude dans l'ouvrage pédagogique qu'est l'Introduction... cette preuve, quelque peu funambule, qu'il a donnée 12 ans plus tôt. Mais vous la trouverez dans notre page spéciale Irrationalité de e (avec les moyens de Terminale).
, pour démontrer. En deux lignes, il élude dans l'ouvrage pédagogique qu'est l'Introduction... cette preuve, quelque peu funambule, qu'il a donnée 12 ans plus tôt. Mais vous la trouverez dans notre page spéciale Irrationalité de e (avec les moyens de Terminale).

dans l'
Introduction à l'Analyse Infitésimale (1748)
Oui, car le simple caractère illimité de ce développement va prouver que e est irrationnel, et c'est précisément par quoi va commencer le paragraphe qui suit.
Les Réduites et la Convergence
Un Algorithme qui reconnaît la Nature des Nombres
Lagrange l'a bien fait remarquer à propos du
rapport des périodes de révolution de Saturne et de la Terre: il est
plus probablement irrationnel que rationnel. L'algorithme employé par
Huygens à la fraction approchée (qui est un nombre rationnel) peut
s'appliquer à tout nombre réel, de la façon qui suit:
Un nombre x (prenons le positif pour simplifier) se décompose en partie entière
(soit le plus petit entier inférieur à x), classiquement notée [x], et sa partie fractionnaire,
parfois notée (x) = x - [x], qui est donc comprise entre 0
(largement) et 1(strictement).
En écartant le cas trivial où x est entier (il n'y a plus rien à faire), on peut alors écrire , avec b = [x] entier et en introduisant
la
quantité y , inverse de
x - [x]
: x - [x] = 1/y,
x = b + 1/y , y > 1
ce
qui permet réitérer. On a donc l'algorithme (la flèche à gauche
signifie que la variable reçoit, prend la valeur, de ce qui est à
droite)
algorithme mathématique
|
algorithme informatique |
b0 = [x] ; r0 = x - b0 ;
tant que rn ≠ 0 faire
bn+1 = [ 1 / rn ] ;
rn+1 = 1 / rn - bn+1 ;
fin tant
|
b ← [x] ; r ← x - b ;
tant que r ≠ 0 faire
y ← 1 / r ; b ← [y] ;
r ← y - b ;
fin tant |
Par souci de simplicité, on n'a
pas fait apparaître le stockage des dénominateurs partiels successifs
dans la version informatique; il convient de ranger les b successifs obtenus (dans un tableau, par exemple). Ce qui nous intéresse à cet instant précis de l'histoire, c'est de savoir si l'algorithme se termine ou pas.
- Si x est rationnel, c'est exactement l'algorithme d'Euclide que l'on effectuera, comme on l'a vu sur l'exemple de Huygens. Il se terminera donc avec un certain rN+1=0, et l'on pourra écrire x sous forme d'une fraction finie
x = [ b0 , b1 , b2 , , ... ,bN ]
- Si x n'est PAS rationnel, l'algorithme ne se terminera pas: dans le cas contraire, il aurait trouvé un reste nul, et recalculant l'expression
x = [ b0 , b1 , b2 , , ... ,bN ]
qui est une suite d'opérations arithmétiques ( +, / ) effectuées
sur des entiers, x serait bien évidemment rationnel. On a prouvé ce
lemme simple mais fondamental:
lemme fondamental d'irrationnalité:
x ∉ ℚ si et seulement si son développement en fraction continuée est illimité.
|
Les Réduites
Ce sont les fractions finies avec "de plus en plus d'étages", que l'on réduit (d'où leur nom) à une forme p / q. Nous avons donné les 4 premières pour le développement de Huygens; de façon générale ce sont
R0 = b0 , R1 = [ b0 , b1 ] , R2 = [ b0 , b1 , b2 ] , ... , Rn = [ b0 , b1 , b2 , ... ,bn ] = Pn / Q n
Ajnsi, pour π
n
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| bn |
3 |
7 |
15
| 1
|
292 |
1 |
1 |
1 |
2 |
1 |
3
|
| Rn |
3 |
|
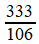
| 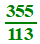
|
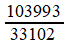
|
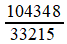
|
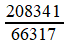
|
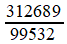
|
...
|
...
|
...
|
Parmi elles, deux sont fort célèbres: R1,
connue d'Archimède, et largement popularisée dans les écoles primaires
par les "hussards noirs de la République", ainsi que R3, dite "de Metius", du nom de l'astronome (1571-1635) qui a publié une formule trouvée par... son père, en 1585. Mais elle avait été découverte bien avant (sous le nom Milü) par le mathématicien chinois Zu-Chongzi (429-500) .
Voyons avec Lagrange leur calcul et leur convergence. Il commence par une affirmation assez péremptoire
|
"Il est d'abord évident que, plus
on prend de termes dans une fraction continue, plus on doit approcher
de la vraie valeur de la quantité qu'on a exprimé par cette fraction;
de sorte que, si l'on s'arrprête successivement à chaque terme de la
fraction, on aura une suite de quantités qui seront nécessairement
convergentes vers la quantité proposée."
Lagrange, Additions aux Éléments d'Algèbre d'Euler (Œuvres, tome 7)
|
Ce n'est pas la seule fois où il affirme avec
aplomb, et il lui est arrivé de se tromper (sur ses polynômes
d'interpolation, dans son cours à l'École Normale de l'An III, par
exemple). Mais il y reviendra un peu plus loin, avec des détails
convaincants. Commençons par le calcul.

|

|
Pas d'indices
généraux dans son texte, observons le: ils ne sont pas encore en
usage. Lettres grecques pour les dénominateurs partiels, majuscules
pour les numérateurs des réduites, majuscules affectées d'un petit
"1".
Ce que Lagrange écrit est la récurrence que suivent les
numérateurs d'une part, les dénominateurs d'autre part. Il s'agit de la même formule, du type linéaire à trois termes, mais avec des initialisations différentes.
Si vous n'aimez pas les indices, tenez vous en à Lagrange, cela doit
suffire pour être convaincu. Si vous préférez une écriture moderne:
| Pn+1 = bn+1 Pn+ Pn-1 |
P0 = b0 |
P-1= 1
|
| Qn+1 = bn+1 Qn+ Qn-1 |
Q0 = 1 |
Q-1= 0 |
L'emploi de l'indice "-1" est une petite ruse esthétique pour inclure les formules donnant P1 et Q1 dans la formule générale.
La preuve est banale, par récurrence.
|
Multipliant la relation des numérateurs par Qn , celle des dénominateurs par Pn
(c'est pourquoi il parle de produit "en croix", en référence à leur
disposition en deux colonnes parallèles qu'il a adoptée) , de façon à
éliminer bn+1 , on a:
Pn+1 Qn - Qn+1 Pn = - ( Pn Qn-1 - Qn Pn-1 )
qu'on peut réitérer jusqu'à P1 Q0 - Q1 P0 = 1, d'où
Pn+1 Qn - Qn+1 Pn = ( -1 )n
C'est l'encadré rouge, dont il déduit, grâce au célèbre théorème de Bézout, que Pn et Qn sont premiers entre eux: toutes les fractions Rn sont donc irréductibles.
Puis, en divisant par le produit Qn Qn+1
C'est le contenu de l'encadré vert.
|

|

|
La convergence va en résulter très rapidement: écrivant
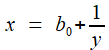 et
et 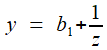 (tous les nombres sont positifs)
(tous les nombres sont positifs)
on tire, à partir de x > b0 et y > b1, par monotonie de la fonction inverse sur les réels positifs
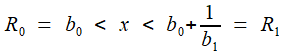 puis
puis 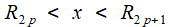
Mais de la formule de récurrence on déduit Qn+1 ≥ Qn+ Qn-1 ≥ 2 Qn-1 ; on en déduit aisément que la suite Qn diverge vers l'infini, ce qui prouve grâce à l'encadrement cidessu le
Théorème fondamental :
Pour tout nombre x réel donné, le développement en fraction continue régulière converge vers x.
|
N.B. : En outre, cette majoration explique n'intérêt de la réduite R3 "de Metius pour π : |π - R3 | < 3×10-7, grâce au "premier quotient négligé", 292, qui pèse de tout son poids sur Q5 . Par
contre, les trois "1" qui suivent n'apportent pas des améliorations
considérables, tout en compliquant la fraction d'approximation.
Des Réduites remarquablement... touristiques
|
Revenons au Nombre d'Or Φ : pour lui, les récurrences sont les plus simples qui soient
| Pn+1 = Pn + Pn-1 |
P0 = 1 |
P-1= 1
|
| Qn+1 = Qn + Qn-1 |
Q0 = 1 |
Q-1= 0 |
On reconnaît la suite de Fibonacci, et comme Q0 = 1, Q1 = 1, la suite Qn n'est que la décalée d'un rang de la suite Pn (elle la reproduit avec un rang de retard)
|

|

|
Leonardo Fibonacci (1175-1250) : sa biographie.
|
Statue de Fibonacci, dans un angle du Camposanto, le vieux cimetière attenant à la Cathédrale de Pise
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
| Pn |
1 |
2
| 3
|
5 |
8 |
13 |
21 |
34 |
55 |
89
|
| Rn |
1
|
2
| 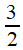
|
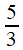
|
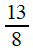
|
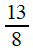
|
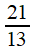
|
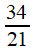
|
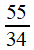
|
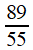
|
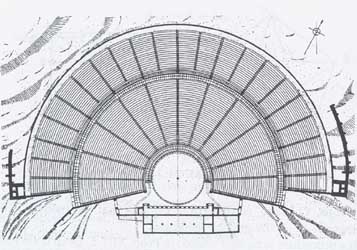
Or, les archéologues ont remarqué l'emploi des termes
mis en gras dans la construction du (grandiose) théâtre d'Épidaure: la partie
inférieure, construite vers 300 av J-C, possède 34
rangées de sièges, et 13 escaliers (un de plus
que les douze travées, puisqu'il y en a un à chaque
bout, bien visible sur les photos). Elle a été
complétée, vers 170 av J-C (mais, semble-t-il,
conformément aux plans initiaux) par 21 rangées
supplémentaires (la délimitation est nette, tant sur les clichés que
sur le plan ci-dessous): cela porte le nombre total de rangées
à 55, par définition de la suite de Fibonacci! Difficile d'imaginer que c'est une simple coïncidence.

|

|
|
Epidaure
(Grèce): le théâtre
|
Son Plan |
On peut, il est vrai, se demander pourquoi le nombre d'escaliers de la
partie supérieure n'a pas été réduit à 21... Il aurait suffi de
supprimer ceux des extrémités! (Ils sont bien présents: on voit
quelqu'un qui monte les marches...)
Non seulement le Nombre d'Or était prisé des Grecs, mais il était
particulièrement chéri des Pythagoriciens. Φ est intimement associé à la
construction du pentagone régulier, et le principe du théâtre repose
sur la division en 10 du demi-cercle (Observez bien le plan: dans chaque
partie, il y a une travée au delà du demi-cercle...) 10 est le nombre
de côtés d'une étoile à 5 branches (ou pentagramme), associée dans la
mystique Pythagoricienne à la santé. Les théâtres grecs faisaient partie
de vastes "ensembles de cure", dirait-on aujourd'hui (le spectacle
soignait l'esprit près de l'endroit où l'on soignait le corps), et selon
les historiens, la volonté de baser secrètement le plan sur le nombre 5
est certaine, et Φ, comme racine de l'équation du second degré x² - x -1 = 0, avait le statut de nombre constructible. L'utilisation des entiers associés aux fractions
d'approximation de Φ s'insérait parfaitement dans un tel mysticisme.
Sans doute faut-il être prudent: il y a des gens qui voient Φ partout,
et cela a suscité des abus. Mais on lit dans [1], qui est une référence
fiable et s'appuie sur des articles documentés:
"It would be very hard to believe that the occurence of Fibonacci
numbers in a building with a fivefold symmetry would be by pure chance"
Précisons enfin qu'il n'y a aucun anachronisme: la suite de Fibonacci
était parfaitement connue des Grecs. Et surtout, ils disposaient d'un
processus, dit d'anthyphérèse, équivalent au développement en fraction
continue, ou, vu d'une autre façon, à l'algorithme d'
Euclide (circa 300 av. J-C).
Un conseil ultime du Mathouriste
: si vous voulez faire une photo comme la sienne, ( et pourquoi pas en
mieux, par exemple avec un objectif à plus grand angle...) allez -y, si vous le
pouvez, le soir, car cela a deux avantages: la lumière et... le vide,
sans les tâches hideuses que font des touristes bariolés et leurs sacs
à dos, généralement choisis d'une teinte jurant le plus possible avec
celle de leur vêtement...
Résoudre des Équations Algébriques avec les Fractions Continuées
Lagrange insère, dans un vaste
traité sur les équations, un chapitre sur l'utilisation des fractions
continuées pour calculer numériquement les racines: la remarquable
vitesse de convegence du développement en fraction continuée (vue
ci-dessus avec la majoration de l'écart) incite à le rechercher "à
partir de l'équation". Cela s'écarte un peu de notre propos sur
l'irrationalité, quoiqu'en apparence seulement: les racines des
équations, hors des rationnelles qui sont très faciles à trouver (grâce
au théorème de divisibilité de Gauss), sont des irrationnels
privilégiés, des nombres algébriques dont la plupart on ne le sait pas encore!- ne peuvent s'exprimer par des superpositions de radicaux.
Disposer d'une méthode efficace et économe en calculs (eh oui, on les
faisait à la main, en ce temps-là!) est alors fort important.
La technique rejoint celle de Huygens: on encadre, par l'étude des
changements de signe du ploynôme, la racine entre deux entiers, p et p+1, ce qui permet de l'écrire
x = p + 1 / y
Voilà qui nous rappelle quelque chose! On varecommencer avec y
, en formant l'équation dont il est racine, résultat de ce changement
de variable dans l'ééquation initiale. Si vous suivez Lagrange, vous
aurez un peu l'impression qu'il vous raconte un conte pour enfants,
façon Les Trois Ours... eh bien, brave gens, c'est un algorithme!
Et après l'exposé du principe, un
exemple pour bien se faire comprendre. Il ne le choisit pas au hasard:
c'est l'équation à laquelle Newton applique sa méthode de la tangente.
Tout en l'égratignant un peu, sans avoir l'air d'y toucher: si elle est
fort précise dans ce cas, elle peut réserver des surprises désagréables
(aller vers une autre racine, cycler, diverger...) alors que la méthode par fraction continue sera toujours convergente, précise, et rapide...
sauf qu'il y a tout de même, si l'on veut regarder honnêtement les deux
plateaux de la balance, le poids de la transformation successive des
équations et la localisation de la racine parmi les entiers et la part
de tâtonnement qu'elle comporte.
Des Fractions Continuées plus générales
Jusqu'ici, nous n'avons considéré que les fractions continuées régulières, celles dont tous les numérateurs partiels
sont des 1. Qu'en est-il de celles qui, comme la fraction "employée"
par Bombelli pour donner la racine carrée de 13, ont la forme la plus
générale, avec des numérateurs partiels quelconques?
En fait, si Huygens inaugure en 1682 le
développement des nombres en fraction régulière, la première fraction
continuée, écrite sous forme d'une cascade de divisions, est une
fraction continuée générale; elle apparaît en 1656 sous la plume de William Brouncker (1620-1684), premier président de la Royal Society, et ami de John Wallis (1616-170), sans qui sa formule nous serait sans doute restée inconnue.
Un disque d'aire π a pour rayon 1; le carré circonscrit est par conséquent de côté 2, si bien que c'est le rapport 4/π
que Brouncker développe. Un an plus tôt, Wallis avait exprimé cette
valeur en un célèbre produit infini, que Brouncker a probablement
transformé par une manipulation formelle. Si la loi de formation est
parfaitement régulière, cette fraction a une piètre vitesse de
convergence, ce qui la rend sans intérêt pratique pour le calcul. Bref,
on a pour π le choix entre une belle
fraction inutile, et une fraction régulière efficace, mais dont la loi
de formation échappe aux mathématiciens; Euler s'y est cassé les dents.
|

|
| Lagrange, Additions aux Éléments d'Algèbre d'Euler (Œuvres, tome 7) |
Voici la citation faite par Wallis, à la fin de son Arithmetica Infinitorum, et reprise dans son Traité d'Algèbre (ci-dessous), il ne donne qu'une vague indication de démonstration, différente de la méthode employée par Brouncker.

|

|

|

|
Wallis,
|
son Traité,
|
et un chapitre de deux demi-pages seulement!
|
Moyennant une adaptation des conditions de convergence (car elle
n'est plus automatique) et du critère d'irrationnalité, ces fractions
peuvent devenir un outil puissant et utile. Toutefois, c'est au prix
d'une montée du niveau technique, et c'est pourquoi nous ne donnerons
plus de détails, mais simplement, deux résultats remarquables.
L'Irrationnalité de π , enfin!
Le vainqueur du sommet, en 1761, s'appelle Johann Lambert (1728-1777) .
Au lieu d'employer un argument direct (c'est à dire, du type de celui d'Euler pour e), il joue le coup de manière indirecte, à partir d'un développement de la fonction tangente: si π/4
était rationnel, sa tangente ne le serait pas... or, elle vaut 1!
La difficulté technique, et le joli tour de force de Lambert réside
dans l'obtention du développement, mais sa rigueur est impeccable;
l'image ci-dessous résume l'agument.
 Elle est pas belle, la fraction de tan?
Elle est pas belle, la fraction de tan?
Une Irrationnalité ... qui avait échappé à Euler!
Euler avait brillamment résolu le problème de Bâle sur
lequel avaient séché Leibniz et les Bernoulli (un des deux frères,
Johann eseignait à Bâle, d'où le nom donné à la question) , : trouver la somme infinie des inverses des carrés d'entiers (vue comme limite des sommes de 1 à N)
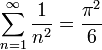
Mais qu'en était-il des autres
puissances? Euler n'était pas homme à laisser une idée de
généralisation de côté, et régla très vite la question des puissances
paires. Mais, malgré diverses tentatives, il ne tira rien du cas des
puissances impaires, et le problème est encore ouvert à ce jour. Même
s'il n'y a pas une jolie valeur en fonction d'une puissance de π, la question de l'irrationalité se pose, à commencer par celle de la somme des inverses des cubes, que l'on note ζ(3) . (Plus généralement, ζ(k) désigne la somme des puissances kièmes).
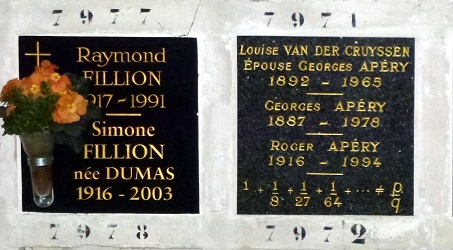
La réponse a été apportée en 1978, par le mathématicien français Roger Apéry, dans un style très eulérien... utilisant une fraction continuée assez extraordinaire. Jugez-en plutôt à son apparition dans un (très bon) article qui la met en évidence!

|
|

|

|
| Au colombarium du Père Lachaise (Paris), le résultat est très sobrement indiqué sur la plaque derrière laquelle repose Apéry. |
Qu'on puisse travailler "comme Euler au XXième
siècle" a d'abord suscité le scepticisme, voire les moqueries. Ceux qui
ont fait preuve d'un esprit ouvert ont beaucoup transpiré, mais comblé
les nombreux vides et finalement proposé... une démonstration expurgée
de fractions continuées. C'est comme si l'histoire de Fourier après
Euler pour e se réécrivait avec ζ(3) !
Bibliographie (relativement) élémentaire
Il
s'agit de livres possédant un chapitre sur le sujet, qu'on peut lire
isolément, avec une approche assez élémentaire. Nous vous recommandons
particulièrement le livre de Jean Itard, encore trouvable en
bibliothèque: difficile de faire plus simple, plus agréable, bien
informé historiquement dans un format aussi condensé. Les fractions
continuées n'y occupent que 25 pages, et le reste est tout aussi instructif; un
opuscule écrit en 1973, à contrecourant d'une époque de mathématiques
coupées de leur histoire, au point de préférer nommer un théorème
(4.6.23.2) plutôt que du patronyme de son découvreur... À méditer!
Bibliographie de référence (pour approfondir)
- [10] C. BREZINSKI, History of Continued Fractions and Padé Approximants (Springer Verlag)
- [11] D. DUVERNEY, Théorie des Nombres (Dunod)
- [12] G. HARDY, E. WRIGHT, An Introduction to the Theory of Numbers (Oxford)
- [13] W.B. JONES, W.J. THRON, Continued Fractions: Analytic Theory and Applications (Addison-Wesley)
- [14] L. LORENTZEN, H.WADELAND, Continued Fractions with Applications (Elsevier)
- [15] I. NIVEN, Irrational Numbers (Wiley)
- [16] I. NIVEN, Numbers: Rational & Irrational (The L. W Singer Company)
- [17] C. OLDS, Continued Fractions (MAA)
- [18] M.SERFATI, Quadrature
du
Cercle, Fractions Continues et Autres Contes (Brochure
APMEP
n°85)
Sur la Toile
Revenir
à la Home
Page du
Mathouriste

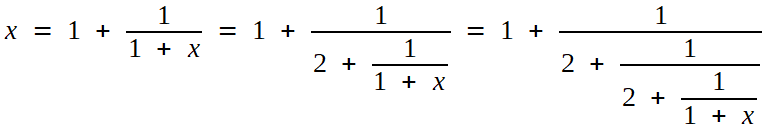

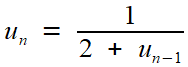
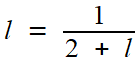 soit
soit 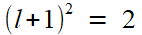 et finalement
et finalement 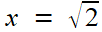




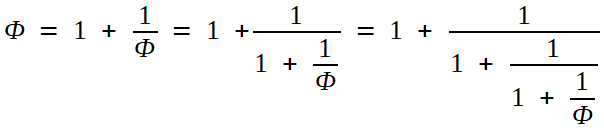
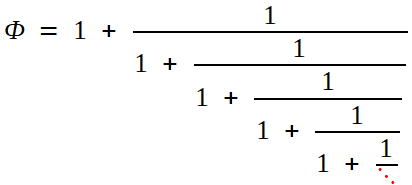
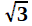
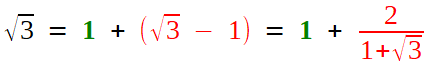
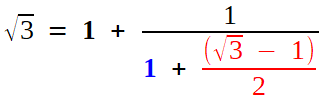
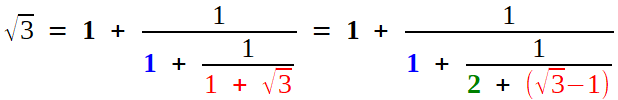
 , dont on était parti. Volià, on peut réitérer, une fois d'abord, et, on espère, indéfiniment.
, dont on était parti. Volià, on peut réitérer, une fois d'abord, et, on espère, indéfiniment.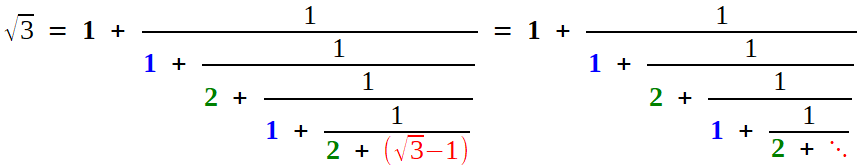
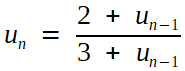
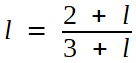 soit
soit 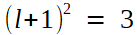
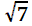 vous donne un peu plus de fil à retordre... nous la soumettrons un peu plus loin.
vous donne un peu plus de fil à retordre... nous la soumettrons un peu plus loin. 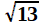


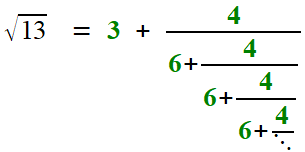
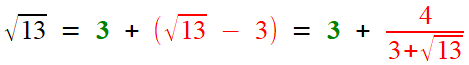
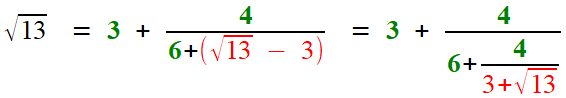
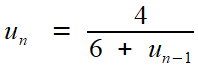

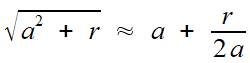
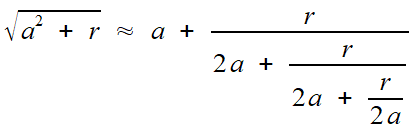
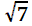



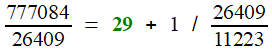
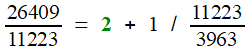
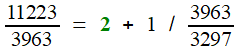
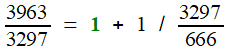
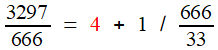
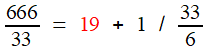
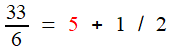
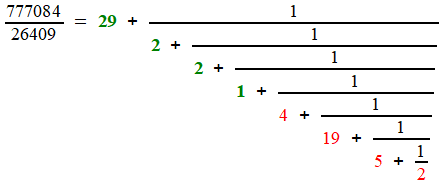
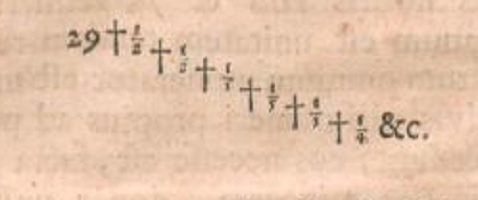
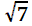
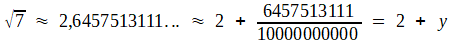

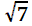 = [ 2, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, ...]
= [ 2, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, 1, 1, 1, 4, ...]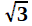
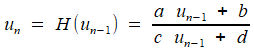 dont la limite vérifie
dont la limite vérifie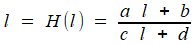

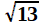 ), à savoir
), à savoir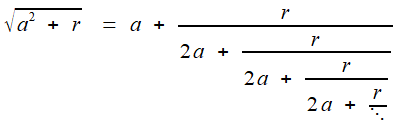
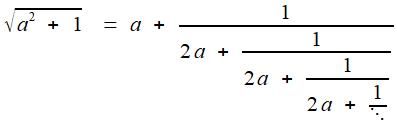
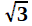
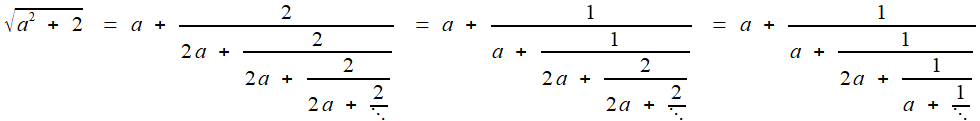
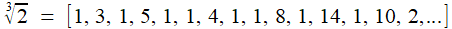


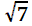 , pour démontrer. En deux lignes, il élude dans l'ouvrage pédagogique qu'est l'Introduction... cette preuve, quelque peu funambule, qu'il a donnée 12 ans plus tôt. Mais vous la trouverez dans notre page spéciale Irrationalité de e (avec les moyens de Terminale).
, pour démontrer. En deux lignes, il élude dans l'ouvrage pédagogique qu'est l'Introduction... cette preuve, quelque peu funambule, qu'il a donnée 12 ans plus tôt. Mais vous la trouverez dans notre page spéciale Irrationalité de e (avec les moyens de Terminale). 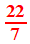
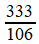
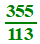
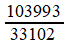
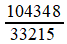
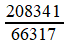
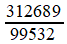
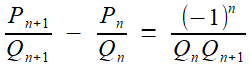


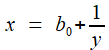 et
et 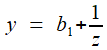 (tous les nombres sont positifs)
(tous les nombres sont positifs) 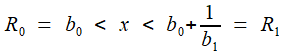 puis
puis 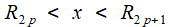
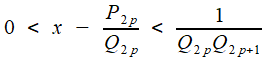 et
et