Identité de BÉZOUT, le (Grand) Retour!
Nous
vous proposons dans cette page de découvrir deux applications modernes,
mais faciles à comprendre, de cette fameuse identité: l'une au plus
célèbre système de chiffrement des messages (dit à clef publique), l'autre au Calcul Formel qui pemet d'effectuer de puissants calculs algébriques sur un simple PC (grâce à des systèmes comme Maple® ou Mathematica®).
Et c'est promis, tout sera prouvé, sans appel à des résultats extérieurs à cette page, et chacune des preuves sera très courte (on garde même le droit de la sauter...).
Les théorèmes ne se périment pas, ils sont éternels... mais les nécessités du temps (au mieux) et les modes (au pire) les mettent en lumière ou dans l'ombre. Les programmes d'enseignement, à la manière des musées, les exposent dans une belle salle ou les relèguent dans une obscure réserve. Celui qu'on présente ici est emblématique de ces flux et reflux: fortement présente dans les années 70, mais dans le cadre triomphant des structures algébriques, l'arithmétique en fut totalement, et sans grand ménagement, évacuée une décennie plus tard, au profit d'une invasion de probabilités & statistiques: cela, au moins, c'était utile, pour ne pas dire indispensable, à la star montante, l'économie mondialisée. Mais voici que l'économie découvre que la science cryptographique peut l'aider à sécuriser les transactions: vite, que l'identité de Bézout revienne dans les cours!
Le pêché d'orgueil des arithméticiens avait été de se comporter en conquérants de l'inutile, et, pire, de le revendiquer: Godfrey Hardy, un des plus grands d'entre eux, se désolait en pacifiste convaincu de voir tant d'applications des mathématiques à des fins militaires; il se consolait en pensant qu'au moins, "l'arithmétique resterait pure spéculation, éloignée des activités humaines, donc noble et propre". Mort en 1947, il pouvait ignorer encore le rôle qu'avait joué l'arithmétique dans la cryptanalyse lors de la seconde guerre mondiale, sujet longtemps protégé du sceau "Confidentiel/Défense". 30 ans plus tard, avec la montée en puissance des ordinateurs et une révolution cryptographique, le doute n'était plus permis: fin de la noblesse et de la propreté... mais grand retour de Gauss et Bézout!
(Petits) Prérequis Arithmétiques
Il fut un temps où la notion de plus grand commun diviseur
était étudiée au collège, à partir de la décomposition en facteurs
premiers d'un entier. Cela fonctionne bien, car la notion est assez
intuitive, et l'application facile:
Mais décomposer un nombre en facteurs premiers n'est pas facile pour un ordinateur -encore moins pour un humain. Non point qu'un programme qui fasse le travail soit difficile à écrire: cela peut être un des premiers exercices de programmation. Le hic est que, si le nombre est grand, un programme correct mettra des années à obtenir le résultat, et cette difficulté, connue aux temps balbutiants des opremiers ordinateurs, reste d'actualité malgré la fulgurante, pour ne pas dire inespérée, montée en puissance des processeurs en un demi-siècle. Autrement dit, il y a une difficulté algorithmique intrinsèque du problème, à laquelle le doublement de vitesse d'un processeur n'apporte aucune réponse, au plus une vaine illusion que l'allongement du nombre à décomposer réduira à néant.
Cette mauvaise nouvelle... est en fait excellente: elle va garantir la sécurité du procédé de cryptographie à clé publique R.S.A. qui va s'appuyer sur le théorème de Bézout!
Mais il y a d'autres moyens de définir et calculer le p.g.c.d. Nous privilégions pour la suite une approche loin d'être la plus générale possible, mais qui a l'immense avantage d'être effective, c'est à dire, ne pas se contenter de dire "il existe..." (avec en sous-entendu, ce pied de nez de l'homme de l'art: "mais débrouillez-vous pour le trouver, ce n'est plus mon affaire!"), mais donner un algorithme efficace (relativement, au moins) pour le calculer.
Cette forte similitude est garante d'une arithmétique similaire, comme on va le constater pour le théorème de Bachet-Bézout.
Appliquons aux diviseurs communs! (On note d | a pour dire que d divise a)
Le calcul de l'exemple ci-dessus devient alors fulgurant: tout diviseur commun à 126 et 120 divise 120 et 6, le premier reste: 6 est alors le plus grand, celui qu'on cherche.
Quel que soit le jeu de stratégie, la victoire en un coup est rare. Mais une arme anodine devient redoutable si on l'applique de façon réitérée! Pour retenir facilement ce principe, faites en un petit proverbe hédoniste, dont l'auteur de ses lignes pense détenir le copyright:
Si on effectue une nouvelle division de b par r, cette fois
Un algorithme apparaît naturellement: tout diviseur commun de a et b divise un autre couple d'entiers positifs de plus en plus petits. Si ce couple finit par être ( ρ , 0 ) , d divise ρ, qui se retrouve de fait plus grand diviseur commun; et sinon... sinon, l'algorithme ne se termine pas (hantise ordinaire de l'informaticien...). Mais cela siginifie qu'on a construit une suite infinie, décroissante, d'entiers strictement positifs, ce qui est impossible. OUF !
Il est difficile de faire plus simple! Si les mathématiciens ont opté pour une définition non constructive, employant la théorie des idéaux, c'est qu'hélas, tous les anneaux ne possèdent pas une division euclidienne. C'est même plutôt une exception! La réponse est certes positive pour l'anneau des entiers de Gauss ℤ [i] = {a + ib; a,b ∈ ℤ}ou ℤ [√2] = {a + b √2; a,b ∈ ℤ}, parce qu'ils disposent d'une application qui prend le relais de la valeur absolue ou du degré dans les deux cas qui nous occupent; mais ils ne sont qu'un nombre fini parmi tous les anneaux de ce type. Pour notre sujet, nous n'avons heureusement pas besoin d'aller plus loin sur la question.
Le point important est désormais le calcul d'un couple de Bézout.
Il se fait en remontant l'algorithme d'Euclide. Voici la marche à suivre sur un exemple: nous allons vérifier que 283 et 77 sont premiers entre eux et déterminer un couple de Bézout; le tour de main pour réussir ce calcul est de laisser les quotients sous forme numérique, mais surtout pas les restes, que l'on substituera de proche en proche! Nous les remplaçons donc par des lettres avec des indices pour cette deuxième phase de l'opération.
Dans la deuxième phase, nous repartons de l'étape 4 écrite 1 = r2 - r3 .12 et l'on y substitue l'expression de r3 que l'on peut tirer de l'étape 3
(u = -37, v = 136) est un couple répondant à la condition de Bézout. Laissons la conclusion à un mathématicien qui fait autorité:
Un (tout petit) peu d'Arithmétique Modulaire
Lorsque nous disons, à 13h, qu'il est 1h, nous faisons de l'arithmétique modulo 12
comme Monsieur Jourdain faisait de prose: nous ne conservons que le
reste d'une division par 12. Et nous savons ausi calculer dans cet
ensemble à 12 symboles: {0, 1, 2, ... 10, 11}: si, à 10h, nous nous
accordons 7h de sommeil avant de faire sonner le réveil pour aller
prendre un avion, nous le réglerons sur 5h, en ayant réduit modulo 12 la somme 10+7=17 = (12)+5. La chose s'écrit symboliquement avec une égalité à trois barres au lieu de deux: 17 ≡ 5 (12)
Le vocabulaire des mathématiciens puise dans cette mage naturelle: avec l'addition, cet ensemble, noté ℤn devient un groupe cyclique, ou encore le groupe de l'horloge. On peut bien sûr remplacer 12 par n'importe quel entier n. C'est encore un groupe de l'horloge, et ceux qu'on voit sourire un peu trop vite ("il n'y a bien que les mathématiciens pour penser qu'une horloge pourrait n'avoir que 11h sur son cadran, ou 13 si l'on est très riche et pas superstitieux") -oui, vous là bas, au fond!!!- feraient bien de visiter les musées parisiens: ils pourront y voir des horloges de l'époque révolutionnaire, avec 10 heures seulement sur leur cadran! Et un peu plus à l'est, ils trouveront de quoi opérer modulo 17 (voir cette page).
La multiplication se fait aussi facilement: on calcule dans les entiers, et on réduit modulo n le résultat. Ainsi la structure d'anneau de ℤ passe-t-elle à ℤn : voici les tables d'addition et de multiplication pour deux valeurs de n petites, mais exemplaires:
On y relève en effet que dans la première, le poduit 2.3 peut être nul sans qu'un des facteurs le soit, puisque 2.3 ≡ 0 (6) : il y a des diviseurs de zéro, ou, cela revient au même: l'anneau ℤ6 n'est pas intègre. Il est immédiat qu'il en va toujours de même si l'entier n est composé.
Dans le deuxième cas, on constate que tout élément non nul a un inverse multiplicatif, ce qui fait de ℤ5 un corps. Et grâce à l'identité de Bézout, on généralise aisément:
♦ Si a est un élément non nul entre 0 et p-1, il est premier avec p, grâce à la primalité de ce dernier. Il existe alors un couple de Bézout (u , v) tel que
Le procédé dispense en outre du calcul complet de la table de multiplication, qui n'est envisageable que pour les petites valeurs.
♦ On peut écrire, en forme développée: a = 1 + k.p = 1 + l.q ; donc k.p = l.q. Ainsi, p | l.q, et comme p est premier avec q, p | l d'après le théorème de divisibilité de Gauss. (Soit dit en passant, ce dernier est aussi une conséquence de l'identité de Bézout, écrite pour p et q, puis multipliée par l) .
Écrivant l = p.r, et reportant, a = 1 + p.q.r , ce qu'il fallait prouver. ♦
Comme le nom (un peu fantaisiste) que nous lui avons donné le suggère, le théorème chinois des restes est un résultat bien plus général, et des documents attestent son utilisation dans la Chine dès l'an 300, alors que Gauss n'a théorisé les calculs sur les résidus modulo n qu'en 1801! Il est un peu plus difficile à démontrer, et nous n'aurons pas besoin de cette forme complète dans notre aventure cryptographique; toutefois, il se trouve étroitement connecté au théorème de Bézout, ce qui justifie cette petite digression.
Notons que notre preuve du lemme 2 n'utilisait que cette forme plus faible de l'hypothèse; ce qui complique un peu le travail pour le "vrai" théorème est la présence de deux restes différents. Il se généralise à un nombre quelconque de congruences, et permettait de faire dénombrer une compagnie de moins de380 soldats -pour évaluer les pertes après une bataille, par exemple- à un sergent ne sachant pas compter plus loin que 12. Voici comment:
Application 1 : le Cryptosystème R.S.A., ... en 2 T-shirts!
Cette découverte qui a révolutionné le monde du chiffrement des
messages en 1978 repose sur le théorème de Bézout et les deux lemmes
cidessus.
Témoignage de la simplicité de l'algorithme, il tient en 5 lignes si célèbres... qu'on les a inscrites sur un T-shirt!!! Tandis qu'un autre présente le concept de clé asymétrique, qui a changé radicalement la conception du chiffrage, et dont R.S.A. constitue une implémentation (ce n'est pas la seule). Les fringues d'abord... ensuite, les explications!
L'art du secret est sans doute aussi vieux que celui de la guerre, mais l'expérience montre deux choses:
Ainsi les I ne sont jamais codés par la même lettre, tandis que Z dans le message crypté a deux valeurs différentes dans le clair: l'attaque statistique ne fonctionne plus de façon basique.
Plus la clef est longue, plus sûr est le système. Mieux: utiliser une clé de même longueur que le message, et la jeter immédiatement après usage, offre une sécurité parfaite: c'est le système de Masque Jetable, inventé en 1913 par l'ingénieur des Bell Labs Gilbert Vernam,(1890-1960) . Un perfectionnement dû au major Joseph Mauborgne est d'utiliser une clé aléatoire pour éviter toute faiblesse de la clé: ainsi, mieux vaut que César code avec une clé aléatoire qu'avec son prénom, ou sa date de naissance, qu'un adversaire essaiera peut-être en pensant que la clé repose sur un procédé mnémotechnique facile.
C'est par l'étude du problème d'échange des clefs que s'amorça le grand tournant: dans un article paru en 1976, New Directions in Cryptography, Whitfield Diffie et Martin Hellman jetaient les bases d'une cryptographie asymétrique, utilisant une clé publique pour coder le message et une clé privée pour le décoder: ce sont les deux clefs différentes (oui, oui, regardez bien leurs dents...) qui apparaissent sur le T-shirt de la jeune femme. Mais ce n'était qu'un principe général, évoquant certes les fonctions à sens unique (faciles à calculer, mais difficiles à inverser sans construire une table entière) et l'emploi de l'arithmétique modulaire, qui rend erratiques, grâce à la réduction modulo N, les fonctions exponentielle ou puissance sans inverse explicite (logarithme, racine) dans ℤN . Cette percée leur a valu le Prix Turing en 2015.
Émoustillés par cet article, quoiqu'un brin sceptiques au premier abord, Ronald Rivest, Adi Shamir et Leonard Adleman concevaient, un an plus tard, le premier système complet à deux clef distinctes, que nous détaillons ci-dessous. Mais ils ont été salués plus rapidement par le Prix Turing, dès 2002! N'hésitez par à lire leur article A Method for Obtaining Digital Signatures and Public-Key Cryptosystems, il est merveilleux de clarté et de simplicité.
Et c'est ainsi que, contrairement à l'usage, l'article ne fut pas signé dans l'ordre alphabétique des auteurs, et que le système qui aurait dû s'appeler ARS gagna la célébrité sous l'acronyme RSA!
Ligne 1 : c'est le choix de la clé secrète, en l'occurrence celui de deux nombres premiers P et Q; il importe qu''ils soient grands en pratique. Ce choix est fait par le destinataire, et lui servira à déchiffrer les messages: il les garde jalousement pour lui. Il complète ce couple par un nombre premier D assez grand, D > max (P , Q) -ceci pour éviter une recherche par essais successifs de son adversaire.
Ligne 2 : c'est la confection de la clé publique, toujours par le destinataire. Il lui est facile de calculer le produit N = P.Q , qu'il peut alors afficher sur sa page web, en compagnie d'un nombre E calculé à partir de D, on va voir comment à la ligne 3.: "Si vous voulez m'écrire, encodez votre message à l'aide de E et N" dit-il à tous ceux qui s'adresseront à lui. N est ainsi connu de tous, mais pas ses facteurs. Il est réputé très difficile de les trouver en un temps raisonnable, mais attention tout de même à ce que cela veut dire: on ne connaît aucun algorithme susceptible de faire ce travail dans un délai acceptable; toutefois, personne n'a prouvé non plus que c'est un problème intrinsèquement difficile, comme on l'a fait pour une foultitude d'autres. On le conjecture fortement...
Ligne 3 : c'est là que le théorème de Bézout entre en action: le destinataire calcule un couple de Bézout pour D et (P-1).(Q-1) : curieuse recette, direz vous, mais nous verrons son intérêt ci-dessous. (Observons qu'il suffit que D soit premier avec (P-1).(Q-1) ; notre choix ne visait qu'à l'assurer sans introduire ce bizarrre produit avant que le T-shirt ne le fasse!
Ligne 4 : Le Message M est encodé par l'expéditeur grâce à la fonction puissance E (comme encodage), calculée modulo N: l'expéditeur a bien tous ses outils à disposition dans la clé secrète; il obtient le message Crypté C , qu'il expédie sans crainte d'interception par un tiers.
Ligne 5 : Le destinataire reçoit C, qu'il déchiffre grâce à sa clé secrète de décodage D. C'est une élévation à la puissance D modulo N: le procédé est le même, mais un nombre secret remplace un nombre public.
♦ Il n'y a plus qu'à expliquer la magie de l'opération: pourquoi ces deux élévations à une puissance sont elles inverses l'une de l'autre?
Mais d'après le lemme 1, pour M ≠ 0, M P-1 ≡ 1 (P) a fortiori M (P-1).(Q-1) ≡ 1 (P) ;
de manière similaire M Q-1 ≡ 1 (Q) puis M (P-1).(Q-1) ≡ 1 (Q) .Nous pouvons alors appliquer le lemme 2 et en tirer
Exemples de problèmes
Nous savons calculer, dans le corps des complexes, l'inverse de 2-3i, et plus généralement de a+bi : il suffit de multiplier haut et bas de la fraction formée par la quantité conjuguée.
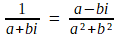
Le même tour de main nous permet de calculer
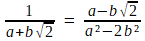
Ainsi, nous faisons des calculs exacts (par opposition à la
détermination de valeurs numériques approchées, la plus fréquemment
réalisée en machine) lorsque les coefficients a et b sont rationnels. Le premier calcul a été réalisé, en fait, dans un ensemble plus petit que ℂ, l'ensemble ℚ [i] des nombres de la forme a+bi , a et b sont rationnels. Le deuxième se déroule dans ℚ [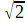 ],
dont la définition est similaire; ces formules établissent que ces
ensembles, dont la structure d'anneau est immédiate, sont aussi des corps, car l'inverse d'un élément s'y trouve aussi.
],
dont la définition est similaire; ces formules établissent que ces
ensembles, dont la structure d'anneau est immédiate, sont aussi des corps, car l'inverse d'un élément s'y trouve aussi.
Les logiciels de calcul formel sont capables d'effectuer des calculs exacts similaires, mais bien plus compliqués. Sans doute peut-on procéder en deux temps avec
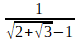
mais cela commence à devenir bien lourd, et saura-t-on encore faire avec
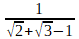
Le bricolage, quand il a cessé d'être instructif, est à proscrire! Il nous faut une méthode; et puis que ferons nous pour calculer
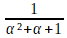 avec pour α la racine réelle de X3 + 2 X + 2 = 0 ?
avec pour α la racine réelle de X3 + 2 X + 2 = 0 ?
Les plus savants des lecteurs savent qu'il y a une formule pour
l'exprimer, aussi belle en théorie qu'assez horrible à manipuler...
mais que l'on change le cube en puissance 5, et, c'est une conséquence
des découvertes de Galois, il n'y a plus de formule!
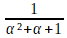 avec pour α la racine réelle de X5 + 2 X + 2 = 0 ?
avec pour α la racine réelle de X5 + 2 X + 2 = 0 ?
Une solution ... qui passe par Bézout!
Les systèmes de calcul formel, Maple® ou autres, manipulent naturellement les polynômes de ℚ [X] : ils peuvent être vus commes des tableaux ou des listes de coefficients. L'ensemble ℚ [α] des expressions P(α) ; où P est un polynôme, peut être manipulé de même; tous les résultats de calcul y sont exprimés en fonction des puissances de α . Mais pour limiter les complications, on va les réduire modulo un polynôme dont α est racine (polynôme annulateur), et même de degré le plus bas possible (on parle alors de polynôme minimal; c'est lui le plus efficace, car il est irréductible; mais il peut être un peu plus difficile à trouver).
Autrement dit, loin de résoudre les équations algébriques par radicaux (quand c'est possible), on transforme les expressions contenant des radicaux en racines de polynômes, sur qui l'on calcule. À titre d'exemple, avec α =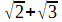 , on a
, on a
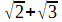 annule M (X) = X4 - 10 X2 + 1.
annule M (X) = X4 - 10 X2 + 1.
Tout polynôme en α peut alors être réduit à un degré inférieur ou égal à 3 par division euclidienne:
♦ Montrons maintenant que tout élément non nul a un inverse; de la preuve résultera une méthode de calcul ne comportant que des somme et produits. R est premier avec M à coup sûr, car celui-ci est irréductible; on peut donc appliquer le théorème de Bézout, et cette fois, c'est vraiment Bézout et non Bachet, car il s'agit de polynômes!
Il existe un couple de Bézout ( U , V ) pour R et M
Exemple 1 : effectuons le calcul demandé plus haut
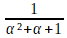 avec pour α la racine réelle de M ( X ) = X3 + 2 X + 2 = 0
avec pour α la racine réelle de M ( X ) = X3 + 2 X + 2 = 0
R ( X ) = X2 + X + 1; on effectue les divisions euclideinnes successives:
Exemple 2 :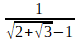
α =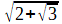 annule M (X) = X4 - 4 X2 + 1.
annule M (X) = X4 - 4 X2 + 1.
Une seule division euclidienne suffit, car le dividende X-1 est de degré 1, donc le reste de degré 0.
Le théorème de Bézout permet ainsi d'effectuer tous les calculs algébriques portant sur des fractions rationnelles sans qu'il y ait une division, et sans aucun calcul approché: toutes les expressions données sont de vraies égalités entre nombres!
Références
Pour commencer
Calcul Formel
Et c'est promis, tout sera prouvé, sans appel à des résultats extérieurs à cette page, et chacune des preuves sera très courte (on garde même le droit de la sauter...).
Les théorèmes ne se périment pas, ils sont éternels... mais les nécessités du temps (au mieux) et les modes (au pire) les mettent en lumière ou dans l'ombre. Les programmes d'enseignement, à la manière des musées, les exposent dans une belle salle ou les relèguent dans une obscure réserve. Celui qu'on présente ici est emblématique de ces flux et reflux: fortement présente dans les années 70, mais dans le cadre triomphant des structures algébriques, l'arithmétique en fut totalement, et sans grand ménagement, évacuée une décennie plus tard, au profit d'une invasion de probabilités & statistiques: cela, au moins, c'était utile, pour ne pas dire indispensable, à la star montante, l'économie mondialisée. Mais voici que l'économie découvre que la science cryptographique peut l'aider à sécuriser les transactions: vite, que l'identité de Bézout revienne dans les cours!
Le pêché d'orgueil des arithméticiens avait été de se comporter en conquérants de l'inutile, et, pire, de le revendiquer: Godfrey Hardy, un des plus grands d'entre eux, se désolait en pacifiste convaincu de voir tant d'applications des mathématiques à des fins militaires; il se consolait en pensant qu'au moins, "l'arithmétique resterait pure spéculation, éloignée des activités humaines, donc noble et propre". Mort en 1947, il pouvait ignorer encore le rôle qu'avait joué l'arithmétique dans la cryptanalyse lors de la seconde guerre mondiale, sujet longtemps protégé du sceau "Confidentiel/Défense". 30 ans plus tard, avec la montée en puissance des ordinateurs et une révolution cryptographique, le doute n'était plus permis: fin de la noblesse et de la propreté... mais grand retour de Gauss et Bézout!
Ce résultat arithmétique devrait plutôt être nommé Théorème de Bachet-Bézout, selon qu'on le situe dans le "décor" (les lecteurs plus savants diront l'anneau) des entiers ou celui des polynômes. Rappleons que si elle appartient légitimement à Bézout pour les polynômes, elle avait été découverte bien avant dans le cas des nombres entiers par un correspondant de Fermat, Bachet de Méziriac (1581-1638).
|
|||||
| personnage célèbre n'hésitant pas à invoquer les deux noms, d'après Hergé, très légèrement (seulement!) modiifée. |
(Petits) Prérequis Arithmétiques
Il fut un temps où la notion de plus grand commun diviseur
était étudiée au collège, à partir de la décomposition en facteurs
premiers d'un entier. Cela fonctionne bien, car la notion est assez
intuitive, et l'application facile:126 = 2.3.3.7 120 = 2.2.2.3.5
p.g.c.d. (126,120) = 2.3= 6
p.g.c.d. (126,120) = 2.3= 6
Mais décomposer un nombre en facteurs premiers n'est pas facile pour un ordinateur -encore moins pour un humain. Non point qu'un programme qui fasse le travail soit difficile à écrire: cela peut être un des premiers exercices de programmation. Le hic est que, si le nombre est grand, un programme correct mettra des années à obtenir le résultat, et cette difficulté, connue aux temps balbutiants des opremiers ordinateurs, reste d'actualité malgré la fulgurante, pour ne pas dire inespérée, montée en puissance des processeurs en un demi-siècle. Autrement dit, il y a une difficulté algorithmique intrinsèque du problème, à laquelle le doublement de vitesse d'un processeur n'apporte aucune réponse, au plus une vaine illusion que l'allongement du nombre à décomposer réduira à néant.
Cette mauvaise nouvelle... est en fait excellente: elle va garantir la sécurité du procédé de cryptographie à clé publique R.S.A. qui va s'appuyer sur le théorème de Bézout!
Mais il y a d'autres moyens de définir et calculer le p.g.c.d. Nous privilégions pour la suite une approche loin d'être la plus générale possible, mais qui a l'immense avantage d'être effective, c'est à dire, ne pas se contenter de dire "il existe..." (avec en sous-entendu, ce pied de nez de l'homme de l'art: "mais débrouillez-vous pour le trouver, ce n'est plus mon affaire!"), mais donner un algorithme efficace (relativement, au moins) pour le calculer.
Division Euclidienne et P.G.C.D. algorithmique
On donne deux entiers relatifs a et b, respectivement deux polynômes A et B. La division euclidienne des entiers n'est autre que celle qu'on apprend (euh... est-ce bien sûr encore?) à l'école primaire pour les entiers naturels. Il en va de même au pays des polynômes (et ce, quel que soit le corps où sont pris leurs coefficients) , à ceci près que le degré vient se substituer à la valeur absolue pour "hiérarchiser" reste et diviseur.| anneau des entiers relatifs ℤ | anneau des polynômes 𝕂 [X] |
| Il existe un unique couple d'entiers ( q , r ) tels que a = b q + r
et 0 ≤ r < |b|
|
Il existe un unique couple de polynômes ( Q , R ) tels que A = B Q + R
et R = 0 ou d° R < d° B |
Cette forte similitude est garante d'une arithmétique similaire, comme on va le constater pour le théorème de Bachet-Bézout.
Appliquons aux diviseurs communs! (On note d | a pour dire que d divise a)
d | a et d | b ⇔ d | b et d | r
Le calcul de l'exemple ci-dessus devient alors fulgurant: tout diviseur commun à 126 et 120 divise 120 et 6, le premier reste: 6 est alors le plus grand, celui qu'on cherche.
Quel que soit le jeu de stratégie, la victoire en un coup est rare. Mais une arme anodine devient redoutable si on l'applique de façon réitérée! Pour retenir facilement ce principe, faites en un petit proverbe hédoniste, dont l'auteur de ses lignes pense détenir le copyright:
Quand c'est bon... on recommence!
Si on effectue une nouvelle division de b par r, cette fois
b = r q' + r' ; 0 ≤ r' < r < |b|
on aura d | a et d | b ⇔ d | b et d | r ⇔ d | r et d | r'
Un algorithme apparaît naturellement: tout diviseur commun de a et b divise un autre couple d'entiers positifs de plus en plus petits. Si ce couple finit par être ( ρ , 0 ) , d divise ρ, qui se retrouve de fait plus grand diviseur commun; et sinon... sinon, l'algorithme ne se termine pas (hantise ordinaire de l'informaticien...). Mais cela siginifie qu'on a construit une suite infinie, décroissante, d'entiers strictement positifs, ce qui est impossible. OUF !
| Théorème : le p.g.c.d. est le dernier reste non nul de l'algorithme d'Euclide. |
Il est difficile de faire plus simple! Si les mathématiciens ont opté pour une définition non constructive, employant la théorie des idéaux, c'est qu'hélas, tous les anneaux ne possèdent pas une division euclidienne. C'est même plutôt une exception! La réponse est certes positive pour l'anneau des entiers de Gauss ℤ [i] = {a + ib; a,b ∈ ℤ}ou ℤ [√2] = {a + b √2; a,b ∈ ℤ}, parce qu'ils disposent d'une application qui prend le relais de la valeur absolue ou du degré dans les deux cas qui nous occupent; mais ils ne sont qu'un nombre fini parmi tous les anneaux de ce type. Pour notre sujet, nous n'avons heureusement pas besoin d'aller plus loin sur la question.
Le point important est désormais le calcul d'un couple de Bézout.
Il se fait en remontant l'algorithme d'Euclide. Voici la marche à suivre sur un exemple: nous allons vérifier que 283 et 77 sont premiers entre eux et déterminer un couple de Bézout; le tour de main pour réussir ce calcul est de laisser les quotients sous forme numérique, mais surtout pas les restes, que l'on substituera de proche en proche! Nous les remplaçons donc par des lettres avec des indices pour cette deuxième phase de l'opération.
| étape |
calcul du p.g.c.d. |
préparation |
| 1 |
283 = 77 x 3 + 52 |
a = b . 3 + r1 |
| 2 |
77 = 52 x 1 + 25 |
b = r1 . 1 + r2 |
| 3 |
52 = 25 x 2 + 2 | r1 = r2 . 2 + r3 |
| 4 |
25 = 2 x 12 + 1 | r2 = r3. 12 + 1 |
1 = r2 - 12 (r1 - r2 . 2 ) = - 12 r1 + 25 r2
Puis on remplace r2 avec l'étape 2 (c'est donc clairement une remontée!) 1 = - 12 r1 + 25 (b - r1 . 1) = 25 b - 37 r1
Et enfin, en utilisant l'étape 1 1 = 25 b - 37 (a - b . 3 ) = - 37 a + 136 b
(u = -37, v = 136) est un couple répondant à la condition de Bézout. Laissons la conclusion à un mathématicien qui fait autorité:
Un (tout petit) peu d'Arithmétique Modulaire
Lorsque nous disons, à 13h, qu'il est 1h, nous faisons de l'arithmétique modulo 12
comme Monsieur Jourdain faisait de prose: nous ne conservons que le
reste d'une division par 12. Et nous savons ausi calculer dans cet
ensemble à 12 symboles: {0, 1, 2, ... 10, 11}: si, à 10h, nous nous
accordons 7h de sommeil avant de faire sonner le réveil pour aller
prendre un avion, nous le réglerons sur 5h, en ayant réduit modulo 12 la somme 10+7=17 = (12)+5. La chose s'écrit symboliquement avec une égalité à trois barres au lieu de deux: 17 ≡ 5 (12)Le vocabulaire des mathématiciens puise dans cette mage naturelle: avec l'addition, cet ensemble, noté ℤn devient un groupe cyclique, ou encore le groupe de l'horloge. On peut bien sûr remplacer 12 par n'importe quel entier n. C'est encore un groupe de l'horloge, et ceux qu'on voit sourire un peu trop vite ("il n'y a bien que les mathématiciens pour penser qu'une horloge pourrait n'avoir que 11h sur son cadran, ou 13 si l'on est très riche et pas superstitieux") -oui, vous là bas, au fond!!!- feraient bien de visiter les musées parisiens: ils pourront y voir des horloges de l'époque révolutionnaire, avec 10 heures seulement sur leur cadran! Et un peu plus à l'est, ils trouveront de quoi opérer modulo 17 (voir cette page).
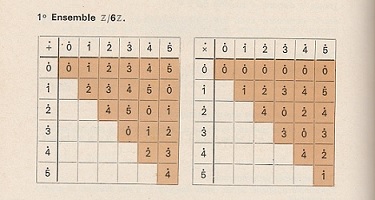
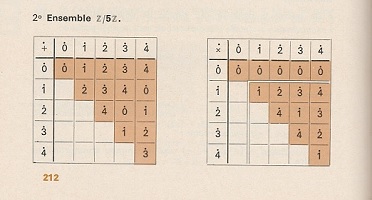
La multiplication se fait aussi facilement: on calcule dans les entiers, et on réduit modulo n le résultat. Ainsi la structure d'anneau de ℤ passe-t-elle à ℤn : voici les tables d'addition et de multiplication pour deux valeurs de n petites, mais exemplaires:
| + et X chez les entiers modulo 6 |
+ et X chez les entiers modulo 5 |
|
 |
 |
 |
| Dans un livre de Terminale mythique, LE "Condamine & Vissio" (1967) |
||
On y relève en effet que dans la première, le poduit 2.3 peut être nul sans qu'un des facteurs le soit, puisque 2.3 ≡ 0 (6) : il y a des diviseurs de zéro, ou, cela revient au même: l'anneau ℤ6 n'est pas intègre. Il est immédiat qu'il en va toujours de même si l'entier n est composé.
Dans le deuxième cas, on constate que tout élément non nul a un inverse multiplicatif, ce qui fait de ℤ5 un corps. Et grâce à l'identité de Bézout, on généralise aisément:
| lemme 0 : si p est un nombre premier, ℤp est un corps: tout élément non nul est inversible. |
♦ Si a est un élément non nul entre 0 et p-1, il est premier avec p, grâce à la primalité de ce dernier. Il existe alors un couple de Bézout (u , v) tel que
a u + p v = 1 soit a u ≡ 1 ( p)
Et c'est donc u, ou plutôt son reste modulo p, qui constituera un inverse. ♦Le procédé dispense en outre du calcul complet de la table de multiplication, qui n'est envisageable que pour les petites valeurs.
| lemme 1 (petit théorème de Fermat): pour tout a, ap ≡ a ( p) ; pour a ≠ 0 , a p-1 ≡ 1 ( p) |
| ♦ La formule du binôme dans permet de développer (a+b) p ; or p premier divise tous les coefficients binômiaux, sauf les deux extrêmes. Il ne reste donc que (a+b) p ≡ a p + b p ( p)
En particulier, avec a = b =1(1+1) p ≡ 1 +1 ( p) soit 2 p ≡ 2 ( p)
ce que l'on peut réitérer immédiatement (a=2, b=1)(2+1) p ≡ 2 +1 ( p) soit 3 p ≡ 3 ( p)
et ainsi de suite. Le deuxième résultat s'obtient en divisant par a, ce dont le lemme 0 garantit la légitimité. ♦ |
Fermat et sa Muse, au Capitole de Toulouse (plus dans notre page Fermat) |
| lemme 2 (TOUT PETIT Chinois) : si p et q sont premiers, a ≡ 1 ( p) et a ≡ 1 (q) ⇒ a ≡ 1 ( pq) |
♦ On peut écrire, en forme développée: a = 1 + k.p = 1 + l.q ; donc k.p = l.q. Ainsi, p | l.q, et comme p est premier avec q, p | l d'après le théorème de divisibilité de Gauss. (Soit dit en passant, ce dernier est aussi une conséquence de l'identité de Bézout, écrite pour p et q, puis multipliée par l) .
Écrivant l = p.r, et reportant, a = 1 + p.q.r , ce qu'il fallait prouver. ♦
Comme le nom (un peu fantaisiste) que nous lui avons donné le suggère, le théorème chinois des restes est un résultat bien plus général, et des documents attestent son utilisation dans la Chine dès l'an 300, alors que Gauss n'a théorisé les calculs sur les résidus modulo n qu'en 1801! Il est un peu plus difficile à démontrer, et nous n'aurons pas besoin de cette forme complète dans notre aventure cryptographique; toutefois, il se trouve étroitement connecté au théorème de Bézout, ce qui justifie cette petite digression.
| Théorème Chinois des Restes : si p et q sont premiers entre eux, a ≡ r ( p) et a ≡ r' (q) ⇒ a ≡ r.r' ( pq) |
Notons que notre preuve du lemme 2 n'utilisait que cette forme plus faible de l'hypothèse; ce qui complique un peu le travail pour le "vrai" théorème est la présence de deux restes différents. Il se généralise à un nombre quelconque de congruences, et permettait de faire dénombrer une compagnie de moins de380 soldats -pour évaluer les pertes après une bataille, par exemple- à un sergent ne sachant pas compter plus loin que 12. Voici comment:

|
Le théorème affirme que la question a une solution unique -donc sans ambiguïté. Le calcul effectif ne demande rien que l'emploi des théorèmes de Bézout et Gauss, donc vous avez tout le matériel nécessaire à ce calcul: c'est pourquoi nous l'avons inclus à titre ludique. N.B. : cette respectable technique ancestrale demeure essentielle dans la manipulation de très grands entiers par les systèmes de calcul formel, car elle économise spectaculairement leur stockage. À titre d'exemple, tout entier positif plus petit que 254 942 590 735 742 7520
peut être représenté de façon unique par ses restes modulo 7015, 6001,
4013, 5017 et 3008, c'est à dire des nombres à 4 chiffres au plus sur
lesquels les calculs seront très rapides. |
Application 1 : le Cryptosystème R.S.A., ... en 2 T-shirts!
Cette découverte qui a révolutionné le monde du chiffrement des
messages en 1978 repose sur le théorème de Bézout et les deux lemmes
cidessus. Témoignage de la simplicité de l'algorithme, il tient en 5 lignes si célèbres... qu'on les a inscrites sur un T-shirt!!! Tandis qu'un autre présente le concept de clé asymétrique, qui a changé radicalement la conception du chiffrage, et dont R.S.A. constitue une implémentation (ce n'est pas la seule). Les fringues d'abord... ensuite, les explications!
| Principe des clés distinctes |
R.S.A.... tout simplement! |
 |
 |
| dans cette affaire de secrets, la jeune femme a évidemment tenu à préserver son anonymat.... |
|
Principes Généraux de Cryptographie, #1 : Ce qu'il ne faut PAS faire!
Un message est certes un texte, mais il peut être converti en nombre, ou en suite de nombres: dans la version la plus naïve, on peut coder chaque lettre par son rang dans l'alphabet (que croyez vous que fasse le code ACSCII d'un ordinateur?). On peut aussi, en utilisant des nombres plus grands, coder des blocs de 4 lettres, de façon quà un bloc corresponde un nombre unique. Nous supposons ce travail fait et travaillons sur des nombres compris dans un intervalle fixé, [0..26] dans le premier cas (en réservant le 0 à l'espace), ou [0..36] si l'on souhaite adjoindre les chiffres, par exemple. C'est évidemment un terrain idéal pour l'emploi de l'arithmétique modulaire.
L'art du secret est sans doute aussi vieux que celui de la guerre, mais l'expérience montre deux choses:
- en dépit du très grand nombre de possibilités (26! = 26x25x...x3x2x1), coder par permutation des lettres n'est pas une bonne idée. Cela ne résiste pas à une attaque statistique, basée sur la fréquence d'occurence d'une lettre dans une langue donnée. Dans le texte "en clair" Français, E a une forte probabilité d'être la lettre qui apparait le plus souvent. Si le texte codé fait apparaître une majorité de R, un espion qui l'a intercepté tentera de remplacer tous les R par des E, essaiera ensuite de substituer le second caractère le plus fréquent, et ainsi de suite. Bien sûr, il y aura des erreurs, des tâtonnements, mais il réduira considérablement le nombre théorique de possibilités. Ce principe remonte au mathématicien arabe Al-Kindi (801-873), auteur du premier ouvrage de cryptanalyse connu (découvert seulement en 1987).
- il ne faut rien espérer du secret qui entourerait le procédé cryptographique; pire, compter dessus serait une faute. C'est l'essentiel du principe de Kerchoffs, aujourd'hui bien admis, mais révolutionnaire à l'époque où Auguste Kerckhoffs (1835-1903) l'énonça dans son article La Cryptographie Militaire (1883) [analyse sur BibNum]
Principes Généraux de Cryptographie, #2 : Clés et Problèmes afférants
Le cryptage reposera donc sur une clef, un texte (ou un nombre) qu'on combinera avec le texte clair pour fabriquer le texte codé. Une manière simple est d'écrire la clef sous le message à encoder (en la répétant si besoin), et additionner terme à terme modulo 26. Exemple avec la clé JULES (très mauvaise idée au demeurant que de coder avec son prénom!): V+J = 22+10 = 32 ≡ 6 (26) = F, etc...
| clair |
V |
E |
N |
I |
V |
I |
D |
I |
V |
I |
C |
I |
| clef | J |
U |
L |
E |
S |
J |
U |
L |
E |
S |
J |
U |
| crypté | F |
Z |
Z |
N |
O |
S |
Y |
U |
A |
B |
M |
D |
Ainsi les I ne sont jamais codés par la même lettre, tandis que Z dans le message crypté a deux valeurs différentes dans le clair: l'attaque statistique ne fonctionne plus de façon basique.
Plus la clef est longue, plus sûr est le système. Mieux: utiliser une clé de même longueur que le message, et la jeter immédiatement après usage, offre une sécurité parfaite: c'est le système de Masque Jetable, inventé en 1913 par l'ingénieur des Bell Labs Gilbert Vernam,(1890-1960) . Un perfectionnement dû au major Joseph Mauborgne est d'utiliser une clé aléatoire pour éviter toute faiblesse de la clé: ainsi, mieux vaut que César code avec une clé aléatoire qu'avec son prénom, ou sa date de naissance, qu'un adversaire essaiera peut-être en pensant que la clé repose sur un procédé mnémotechnique facile.
|
Puisqu'il y a un système parfait, pourquoi ne pas l'utiliser, et afficher le mot fin sur l'histoire de la cryptographie? Il n'y a qu'un ennui: cette clé unique doit rester secrète, et comment
faire pour l'envoyer préalablement en toute sécurité à l'autre bout de
la ligne? C'est le casse-tête majeur de la cryptographie. Le célèbre Téléphone Rouge
utilisait le système de Vernam, les clés étant transmises par... la
valise diplomatique.
La machine ENIGMA de la Wehrmacht était aussi
géniale par sa simplicité de conception que par sa complexité de
cryptage (voir notre encadré dans cette page)
, mais il fallait transmettre quotidiennement la position des rotors de
cryptage/décryptage qui construisaient la clef, et là, la sécurité
n'était plus totale, puisque cela se faisait grâce à un carnet de codes
(emporté par les U-Boots en début de mission) qui pouvaient tomber aux
mains de l'ennemi... et c'est arrivé. Notons que la machine respectait
parfaitement le principe de Kerchoffs: dès avant la guerre, les alliés
connaissaient en détail son principe, sans que cela les aidât à
déchiffrer: il fallut l'ingéniosité des cryptographes polonais, puis d'Alan Turing pour venir à bout de la tâche.
|
|
| Machine ENIGMA de la Kriegsmarine, à 4
rotors |
C'est par l'étude du problème d'échange des clefs que s'amorça le grand tournant: dans un article paru en 1976, New Directions in Cryptography, Whitfield Diffie et Martin Hellman jetaient les bases d'une cryptographie asymétrique, utilisant une clé publique pour coder le message et une clé privée pour le décoder: ce sont les deux clefs différentes (oui, oui, regardez bien leurs dents...) qui apparaissent sur le T-shirt de la jeune femme. Mais ce n'était qu'un principe général, évoquant certes les fonctions à sens unique (faciles à calculer, mais difficiles à inverser sans construire une table entière) et l'emploi de l'arithmétique modulaire, qui rend erratiques, grâce à la réduction modulo N, les fonctions exponentielle ou puissance sans inverse explicite (logarithme, racine) dans ℤN . Cette percée leur a valu le Prix Turing en 2015.
Émoustillés par cet article, quoiqu'un brin sceptiques au premier abord, Ronald Rivest, Adi Shamir et Leonard Adleman concevaient, un an plus tard, le premier système complet à deux clef distinctes, que nous détaillons ci-dessous. Mais ils ont été salués plus rapidement par le Prix Turing, dès 2002! N'hésitez par à lire leur article A Method for Obtaining Digital Signatures and Public-Key Cryptosystems, il est merveilleux de clarté et de simplicité.
Et c'est ainsi que, contrairement à l'usage, l'article ne fut pas signé dans l'ordre alphabétique des auteurs, et que le système qui aurait dû s'appeler ARS gagna la célébrité sous l'acronyme RSA!
R.S.A. en 5 lignes... avec Bézout en clef de voûte
Nous commentons ici la quintessence de l'algorithme, telle qu'elle se présente sur le T-shirt (suggestion: réaffichez le dans une autre fenêtre!).Ligne 1 : c'est le choix de la clé secrète, en l'occurrence celui de deux nombres premiers P et Q; il importe qu''ils soient grands en pratique. Ce choix est fait par le destinataire, et lui servira à déchiffrer les messages: il les garde jalousement pour lui. Il complète ce couple par un nombre premier D assez grand, D > max (P , Q) -ceci pour éviter une recherche par essais successifs de son adversaire.
Ligne 2 : c'est la confection de la clé publique, toujours par le destinataire. Il lui est facile de calculer le produit N = P.Q , qu'il peut alors afficher sur sa page web, en compagnie d'un nombre E calculé à partir de D, on va voir comment à la ligne 3.: "Si vous voulez m'écrire, encodez votre message à l'aide de E et N" dit-il à tous ceux qui s'adresseront à lui. N est ainsi connu de tous, mais pas ses facteurs. Il est réputé très difficile de les trouver en un temps raisonnable, mais attention tout de même à ce que cela veut dire: on ne connaît aucun algorithme susceptible de faire ce travail dans un délai acceptable; toutefois, personne n'a prouvé non plus que c'est un problème intrinsèquement difficile, comme on l'a fait pour une foultitude d'autres. On le conjecture fortement...
Ligne 3 : c'est là que le théorème de Bézout entre en action: le destinataire calcule un couple de Bézout pour D et (P-1).(Q-1) : curieuse recette, direz vous, mais nous verrons son intérêt ci-dessous. (Observons qu'il suffit que D soit premier avec (P-1).(Q-1) ; notre choix ne visait qu'à l'assurer sans introduire ce bizarrre produit avant que le T-shirt ne le fasse!
À ce stade, les clés sont bien définies: la clé publique est le couple ( N , E ) et la clé secrète, le triplet ( P, Q, D ).
Ligne 4 : Le Message M est encodé par l'expéditeur grâce à la fonction puissance E (comme encodage), calculée modulo N: l'expéditeur a bien tous ses outils à disposition dans la clé secrète; il obtient le message Crypté C , qu'il expédie sans crainte d'interception par un tiers.
Ligne 5 : Le destinataire reçoit C, qu'il déchiffre grâce à sa clé secrète de décodage D. C'est une élévation à la puissance D modulo N: le procédé est le même, mais un nombre secret remplace un nombre public.
♦ Il n'y a plus qu'à expliquer la magie de l'opération: pourquoi ces deux élévations à une puissance sont elles inverses l'une de l'autre?
C D ≡ M ED (N) ≡ M. M ED - 1 (N)
soit C D ≡ M. M k.(P-1).(Q-1) (N)
avec k entier, en appliquant l'identité de Bézout. .soit C D ≡ M. M k.(P-1).(Q-1) (N)
Mais d'après le lemme 1, pour M ≠ 0, M P-1 ≡ 1 (P) a fortiori M (P-1).(Q-1) ≡ 1 (P) ;
de manière similaire M Q-1 ≡ 1 (Q) puis M (P-1).(Q-1) ≡ 1 (Q) .Nous pouvons alors appliquer le lemme 2 et en tirer
M (P-1).(Q-1) ≡ 1 ( N)
puis C D ≡ M ED (N) ≡ M (N)
Le résultat est en outre évident si M ≡ 0.♦ puis C D ≡ M ED (N) ≡ M (N)
Application 2 : le Calcul Formel
Exemples de problèmes
Nous savons calculer, dans le corps des complexes, l'inverse de 2-3i, et plus généralement de a+bi : il suffit de multiplier haut et bas de la fraction formée par la quantité conjuguée.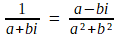
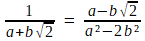
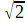 ],
dont la définition est similaire; ces formules établissent que ces
ensembles, dont la structure d'anneau est immédiate, sont aussi des corps, car l'inverse d'un élément s'y trouve aussi.
],
dont la définition est similaire; ces formules établissent que ces
ensembles, dont la structure d'anneau est immédiate, sont aussi des corps, car l'inverse d'un élément s'y trouve aussi.Les logiciels de calcul formel sont capables d'effectuer des calculs exacts similaires, mais bien plus compliqués. Sans doute peut-on procéder en deux temps avec
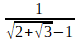
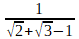
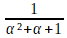 avec pour α la racine réelle de X3 + 2 X + 2 = 0 ?
avec pour α la racine réelle de X3 + 2 X + 2 = 0 ?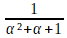 avec pour α la racine réelle de X5 + 2 X + 2 = 0 ?
avec pour α la racine réelle de X5 + 2 X + 2 = 0 ?Une solution ... qui passe par Bézout!
Les systèmes de calcul formel, Maple® ou autres, manipulent naturellement les polynômes de ℚ [X] : ils peuvent être vus commes des tableaux ou des listes de coefficients. L'ensemble ℚ [α] des expressions P(α) ; où P est un polynôme, peut être manipulé de même; tous les résultats de calcul y sont exprimés en fonction des puissances de α . Mais pour limiter les complications, on va les réduire modulo un polynôme dont α est racine (polynôme annulateur), et même de degré le plus bas possible (on parle alors de polynôme minimal; c'est lui le plus efficace, car il est irréductible; mais il peut être un peu plus difficile à trouver). Autrement dit, loin de résoudre les équations algébriques par radicaux (quand c'est possible), on transforme les expressions contenant des radicaux en racines de polynômes, sur qui l'on calcule. À titre d'exemple, avec α =
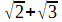 , on a
, on a(α - 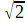 ) ² = 3, soit
) ² = 3, soit
α² - 1 = 2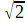 α , d'où
α , d'où
( α² - 1 )2 = 4.2.α²
En développant, on voir que α = 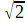 ) ² = 3, soit
) ² = 3, soitα² - 1 = 2
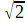 α , d'où
α , d'où( α² - 1 )2 = 4.2.α²
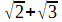 annule M (X) = X4 - 10 X2 + 1.
annule M (X) = X4 - 10 X2 + 1.Tout polynôme en α peut alors être réduit à un degré inférieur ou égal à 3 par division euclidienne:
P ( X ) = M ( X ) . Q ( X ) + R ( X ), d'où
P ( α ) = 0 . Q ( α ) + R ( α ) = R ( α )
P ( α ) = 0 . Q ( α ) + R ( α ) = R ( α )
♦ Montrons maintenant que tout élément non nul a un inverse; de la preuve résultera une méthode de calcul ne comportant que des somme et produits. R est premier avec M à coup sûr, car celui-ci est irréductible; on peut donc appliquer le théorème de Bézout, et cette fois, c'est vraiment Bézout et non Bachet, car il s'agit de polynômes!
Il existe un couple de Bézout ( U , V ) pour R et M
1 = U ( X ) . R ( X ) + V ( X ) . M ( X )
1 = U ( α ) . R ( α ) + V ( α ) . 0 = U ( α ) . R ( α )
♦1 = U ( α ) . R ( α ) + V ( α ) . 0 = U ( α ) . R ( α )
Exemple 1 : effectuons le calcul demandé plus haut
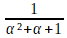 avec pour α la racine réelle de M ( X ) = X3 + 2 X + 2 = 0
avec pour α la racine réelle de M ( X ) = X3 + 2 X + 2 = 0 M ( X ) = R ( X ) . (X - 1) + ( 2 X + 3 ) = R ( X ) . (X - 1) + S ( X )
R ( X ) = S ( X ). (½ X - ¼) + 7/4
On peut à présent "remonter":R ( X ) = S ( X ). (½ X - ¼) + 7/4
7/4 = R ( X ) - S ( X ). (½ X - ¼)
7/4 = R ( X ) - [M ( X ) - R ( X ) . (X - 1) ]. (½ X - ¼)
7/4 = R ( X ) [ 1 + (½ X - ¼)(X - 1) ] - (½ X - ¼) M ( X )
en réduisant, on a7/4 = R ( X ) - [M ( X ) - R ( X ) . (X - 1) ]. (½ X - ¼)
7/4 = R ( X ) [ 1 + (½ X - ¼)(X - 1) ] - (½ X - ¼) M ( X )
7 = R ( X ) [ 2 X2 - 3 X + 5 ] - (2 X - 1) M ( X )
d'où7 = R ( α ). [ 2 α 2 - 3 α + 5 ] + 0
i.e;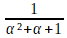 = (2 α 2 - 3 α + 5) / 7
= (2 α 2 - 3 α + 5) / 7
i.e;
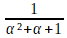 = (2 α 2 - 3 α + 5) / 7
= (2 α 2 - 3 α + 5) / 7Exemple 2 :
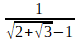
α =
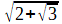 annule M (X) = X4 - 4 X2 + 1.
annule M (X) = X4 - 4 X2 + 1.Une seule division euclidienne suffit, car le dividende X-1 est de degré 1, donc le reste de degré 0.
X4 - 4 X2 + 1 = ( X - 1 ) ( X3 + X2 - 3 X - 3 ) - 2, d'où
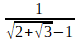 = ½ ( α3 + α2 - 3 α - 3 )
= ½ ( α3 + α2 - 3 α - 3 )
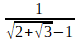 = ½ ( α3 + α2 - 3 α - 3 )
= ½ ( α3 + α2 - 3 α - 3 ) Le théorème de Bézout permet ainsi d'effectuer tous les calculs algébriques portant sur des fractions rationnelles sans qu'il y ait une division, et sans aucun calcul approché: toutes les expressions données sont de vraies égalités entre nombres!
Références
Cryptographie, Histoire
- David KAHN, La Guerre des Codes Secrets (Interéditions)
- Simon SINGH, Histoire des Codes Secrets (J.C. Lattès)
Cryptographie & Arithmétique
Pour commencer
- Un cours de base en Arithmétique et Cryptographie (en ligne, source: Université de Lille, donné en MOOC)
- M. ABDELJAOUAD, Introduction à l'Arithmétique (Centre de Publications Universitaires de Tunis)
- D. BARSKY, Cryptologie (en ligne, cours à l'Université Paris 13)
- B. BECKETT, Introduction aux Méthodes de la Cryptologie (Masson)
- C. BACHOC, Codes et Cryptologie (en ligne, cours de L1 à l'Université de Bordeaux)
- R. FRIEDBERG, An Adventurer's Guide to Number Theory (Dover)
- J. HOFFSTEIN, J. PIPHER, J. SILVERMAN, An Introduction to Mathematical Cryptolgraphy (Springer)
- G. ZEMOR, Cours de Cryptographie (Cassini)
Pour approfondir
- M. DEMAZURE, Cours d'Algèbre (Cassini)
- J.G. DUMAS, J.L. ROCH, E. TANNIER, S. VARRETTE, Théorie des Codes (Cassini)
- P. NAUDIN, C. QUITTÉ, Algorithmique Algébrique (Masson)
- B. SCHNEIER, Cryptographie Appliquée (Thomson Publishing)
Calcul Formel
- P. SAUX-PICART, Cours de Calcul Formel (Ellipses)
Revenir à la Home Page du Mathouriste


