BÉZOUT, LE théorème
Voilà un résultat qui plaide pour l'idée selon laquelle on découvre les mathématiques, et... qu'on invente les méthodes et les outils de la preuve.
Petits rappels: un monôme en deux variables x, y a pour degré la somme des degrés en x et y; par exemple x3 y2 est de degré 5. Le degré d'un polynôme est le plus grand degré de ses monômes; une courbe algébrique l'ensemble des points du plan où il s'annule: P (x, y) = 0.
Le Théorème de Bézout existe en deux versions:
Commençons par un avis d'expert:
Notre dernière ligne donne le nombre de points d'intersection "ressentis". Eh oui, comme avec les prévisions météo, dans les problèmes d'intersection, il y a le mesuré et le ressenti!
Les exemples proposés ont été choisis pour éviter des calculs trop compliqués. En particulier, former l'équation aux abcisses des intersections (résolvante) se fait par simple report dans tous les cas sauf un, où l'on gagne en deux coups.
EX 1 : l'équation résolvante est x2 + ( x3 - 4 x )2 - x - 8 = 0, soit
Elle n'a rien de très souriant, bien sûr, mais nous pouvons confier à une machine sa résolution numérique et confirmer qu'elle a 6 racines. L'appartion du degré 6 résulte simplement de la substitution d'un terme de degré 3 en x de la cubique dans un terme carré de la conique.
EX 2 : l'équation résolvante est :
Elle n'a qu'une seule racine réeelle, entre 1 et 2, comme l'étude des variations le montre élémentairement. Sa positivité permet de trouver deux solutions en y correspondantes, il n'y a donc que deux points réeels d'intersection.
EX 3 : l'équation résolvante est
On comprend dès ce moment que l'étude va inévitablement rencontrer la question du nombre de racines d'un plunôme de degré n. C'est donc sans doute le bon endroit pour rappeler deux faits importants, qu'il convient de ne pas mélanger, car le premier est élémentaire, et le second beaucoup moins.
TH A : un polynôme de degré n a au plus n racines.
TH B (théorème fondamental de l'Algèbre, dit aussi de d'Alembert-Gauss) : un polynôme de degré n a exactement n racines, dans le corps des complexes.
Le premier résulte de la divisibilité par X - α lorsque α est racine, et de la théorie du degré. Le second n'est pas démontré à l'époque de Bézout, même s'il est largement pressenti. Et inexorablement, l'étude des courbes algébriques va glisser vers le domaine complexe au siècle suivant, pour pouvoir énoncer des résultats généraux.
Mais revenons à nos exemples.
EX 4 : l'équation résolvante est :
On obtient en tout, avec ce premier exemple de multiplicité d'une intersection, 4 points réels (et deux imaginaires supplémentaires, pour arriver à 6 en tout)
EX 5 : l'équation résolvante s'obtient cette fois en deux temps. On remplace l'expression du cercle par le report de y2 tiré de la seconde:
Cela a abaissé le degré en y de la première (on voit ainsi se dessiner une méthode systématique), qui permetd'expliciter y et de reporter dans la seconde. le degré 6 de la résolvante s'explique bien par 3x2.
EX 6 : l'équation résolvante s'obtient de nouveau par simple report, et elle est de degré 3; c'est un effet de la symétrie mutuelle des deux courbes (pas de terme en y, donc pas de deuxième étape de report):
Une hyperbole, une parabole... et une excursion lointaine
Les exemples précédents ont fait ressentir la nécessité de prendre en
compte, si l'on veut espérer un dénombrement exact donné par le produit
des degrés, l'existence de points imaginaires et les divers aspects de
la multiplicité. Ce n'est pourtant encore pas tout, comme le prouvera
l'exemple ci-dessous.
En résumé, pour avoir un théorème de Bézout "fort" (le nombre de points d'intersection de deux courbes algébriques est égal au produit de leurs degrés), il faut accepter les points imaginaires, les points à l'infini, et les multiplicités, soit d'un point sur une courbe, soit de l'intersection si les courbes ont un contact "plus proche" (par ex. être tangentes correspond à une multiplicité 2). La simplicité du résultat est à ce prix... les mathématiciens n'ont pas compliqué par plaisir; ils ont été poussé à considérer les courbes dans ces espaces ambiants plus grands que le plan usuel pour continuer à travailler efficacement et produire des résultats.
Le démontrer en basse dimension ?
L'idée peut vous paraître saugrenue; historiquement, elle ne l'est pas
tant que cela, comme on le verra.
Deux droites (degré 1 et 1):
Deux droites d'équations a x + b y +
c = 0 et u x + v y + w = 0
se coupent en un point unique... sauf si elles sont parallèles. Mais en
ce cas, elles partagent la même direction (-b,a). Dans les coordonnées
homogènes de la géométrie projective,
x = X/T, y = Y/T, ces
droites ont pour équations
En choisisant un repère adapté, la première peut-être mise en forme "semi-réduite" y2 = a x2+ b x + c = Q(x) -que nous appelons ainsi parce que cest la première étape vers les formes réduites en repère quelconque. La seconde aura la forme la plus générale
en l'ordonnant en y; l'indice du ploynôme en x indique son degré maximal. Comme dans l'EX 5, l'élimination de y se conduit en deux temps: un premier report fait disparaître les y2 de la seconde, abaissant son degré à 1; dans un second temps le report de l'expression rationnelle en x obtenue pour y fournira la résolvante en x:
C'est la méthode d'abaissement du degré. Comme on l'a déjà indiqué, la tactique consistant à conserver celle des deux équations que l'on reporte dans l'autre est simple et sûre pour éviter tout ajout de solution parasite. L'équation obtenue est clairement de degré inférieur ou égal à 4, sans que l'on puisse dire plus, car on soustrait deux termes de degré inférieur ou égal à 4. Voici une description d'époque du procédé, par un illustre auteur, responsable des articles scientifiques de l'ouvrage:
Exercice: le calcul est encore moins volumineux à partir d'une des formes réduites y2 = x , y2 - x2 = 1 , y2 - x2 = 1, mais il faut s'y reprendre à trois fois...
Méthode 2 : utiliser un paramétrage pour une des deux coniques
C'est une situation idéale pour étudier une intersection que de disposer d'une courbe sous forme paramétrée et de l'autre en cartésiennes, car l'étude de l'intersection dse fait par simple report. Prenons pour origine un point sur la première conique, et coupons par une sécante variable issue de ce point:
autrement dit, x et y sont des fractions rationnelles en t dont les degrés du numérateur et du dénominateur n'excèdent pas 2, et, point extrêment important, le dénominateur est le même pour les deux ; c'est de là que vient le fait que le degré de l'équation aux paramètres t de l'intersection ne dépassera pas 4; c'est, après avoir chassé les dénominateurs
C'est une somme de 6 termes dont aucun n'a un degré qui dépasse 4.
Méthode 3 : se ramener à un cas plus facile
Avec un simple report, on règle le cas d'une conique et d'une droite: deux points d'intersection au plus, deux exactement en admettant points imaginaires ou points à l'infini. Si l'on considère le cas trivial où l'une des deux coniques est décomposée en deux droites, le résultat est aussi simple que... 2 x 2 = 4. Peut-on s'y ramener?
Le système des deux équations qui définit l'intersection des deux coniques est
La question est alors naturelle: peut-on trouver un tel que la deuxième soit une coniques décomposée en deux droites? Il est facile de voir que cela revient à ce que cette conique possède un point double. Un petit calcul auxiliaire donne pour cela une équation du trosième degré en λ, ce qui assure qu'uelle aura au moins une racine réelle, et l'affaire sera encore résolue!
Encore des exemples!
Juste pour se rappeler que multiplicités et rencontres à l'infini demeureront de la partie.
Voici d'abord une ellipse et un cercle, passant tous deux par O... et un autre point à coordonnées positives (cliquer sur les images zoomées pour mieux voir!). Sans calcul: il est évident que l'ellipse et le cercle ont même tangente x - 2y = 0 , donc O est au moins point double... mais que voit-on si l'on effectue un petit développement limité des deux fonctions donnant localement y en fonction de x ? (pas besoin d'être un savant connaisseur du théorème des fonctions implicites: il est évident qu'on peut donner des formules explicites, tellement moches qu'on ne les explicitera surtout pas:! Mais cela ne les empêche pas de garantir existence et régularité de ces fonctions, on peut alors calculer les développements par coefficients indéterminés)
On prouvera ce que nos yeux voient : leur différence est d'ordre 3: les deux courbes se traversent en changeant de position relative; le cercle est au dessus de l'ellipse à gauche de O, en dessous à droite. Les 4 points d'intersection sont réeels, O est triple.
Votre serviteur a utilisé le cercle de courbure de l'ellipse au point considéré; il est parmi les cercles tangents à l'ellipse le seul à avoir un contact d'ordre au moins (et, ici, exactement) 3; on peut du reste facilement voir que tout autre cercle tangent ( contact d'ordre 2) reste, soit intérieur, soit extérieur à l'ellipse en O.
Allons maintenant à l'infini, voir ce qui s'y passe...
Dans l'EX 9, les deux hyperboles ont trois points réels d'intersection; le dernier, à l'infini, représente la direction asymptotique commune x = 0. Les asymptotes respectives, x = 0 et x = 2, sont distintres.
Dans l'EX 10, les deux hyperboles ont deux points réels d'intersection; le dernier, à l'infini, représente toujours la direction asymptotique commune x = 0. Mais il est double, car les courbes ont cette fois la même asymptote x = 0, situation comparable à la propriété d'avoir même tangente à distance finie.
On remarque immédiatement (simple report de y = 1/x que la résolvante aux abcisses est de degré 3 = 4-1 pour le premier (un point à l'infini), 2 = 4-2 pour le second (un point double à l'infini)
N.B. : nous avons ici déterminé l'intersection de deux coniques en résolvant une équation du quatrième degré (en général). Mais "travailler en sens inverse" a aussi son intérêt: ramener la résolution d'une équation algébrique à l'intersection de deux coniques. C'est ce qu'a proposé le grand mathématicien persan Omar al-Khayyam (1048-1131) pour résoudre les équations du troisième degré: il ajoute la racine"factice" 0 en multipliant par x, et construit deux coniques, les plus simples possibles, dont les abbcisses d'intersection sont 0 et les racines de la proposée. Nous vous en reparlerons bientôt dans une page spéciale!
Méthode 2 : utiliser un paramétrage d'une des deux cubiques
On l'a dit plus haut, c'est idéal pour étudier une intersection que de disposer d'une courbe sous forme paramétrée et de l'autre en cartésiennes... et cela n'a rien à voir avec le degré! Avec pour l'une d'elles
P, Q, R étant des polynômes de degré inférieur ou égal à 3 pour représenter l'une, avec le même dénominateur R; et l'autre sous sa forme la plus générale
le report donnera une équation en t de degré inférieur ou égal à 3 x 3 = 9; il n'est guère besoin d'explicitertout pour s'en convaincre. Le seul point important est que c'est le même dénominateur R3que l'on chasse pour retrouver une équation polynômiale.
Tout irait pour le mieux dans le meilleur des mondes si toute cubique admettait un paramétrage rationnel... mais ce n'est pas le cas!
En fait, un paramétrage rationnel ne tient que pour les cubiques à point double. Si on place l'origine en un tel point de g (x, y) = g3 (x, y) + g2 (x, y) +g1 (x, y) +L' = 0, la constante est nulle; et si ne l'est pas, la courbe a une disposition d'arc régulier dont la tangente est g1 (x, y) = 0. Coupant par y = tx on a (si vous ne le voyez pas sous cette forme résumée, développez ces expressions)
d'où la forme attendue. Cela, c'est la partie facile; il faut un peu plus de travail pour montrer qu'en l'absence de point double, pas de paramétrage rationnel... et cela n'avancerait guère notre propos.
Méthode 1 : utiliser l'équation réduite d'une des deux cubiques
Sans nous interroger sur son origine, provisoirement au moins, admettons qu'un bon choix de repère nous donne, pour la première, une forme "semi-réduite", qui apparait assez proche de celle des conqieus rencontrée précédemment, à savoir
La résolvante sera
Revenons maintenant sur le lemme utilisé... et son illustre auteur:
Voici, dans la traduction anglaise (l'original est en latin), les deux pages où Newton présente les 5 formes de paraboles divergentes, et celle de son affirmation, que nous traduisosns en Français.
Oui, MAIS !!!!
Comment prouve-t-on, le plus généralement, ce résultat sur lequel nous nous appuyons? Écrire qu'un point est d'inflexion -c'est à dire que la tangente y a un ordre de contact avec la courbe, au moins égal à 3 (et donc égal, dans le cas d'une cubique!) mène (élémentairement, sans théorie génrale sur la Hessienne) à situer le point sur une autre courbe du troisième degré... et à conclure, par le théorème de Bézout, que les deux ont neufs points en commun, donc nécessairement, un au moins réel.
Et nous venons donc de fabriquer un magnifique cercle vicieux!!!
Les preuves de Clairaut et Nicole évoquées ci-dessus par Gomes-Teixeira (et que mentionne aussi Cramer) semblent exemptes de cette perfide circularité, mais la contrepartie est la longueur des calculs (et la typographie de l'époque n'en rend pas la présentation très agréable...). on se fera une opinion en les consultant sur Gallica (BnF) : Clairaut (pp 483-493) et Nicole (pp 494-511, 3 planches hors pagination à la suite) les deux se trouvent l'un derrière l'autre dans le recueil de l'Académie.
mais patience... nous pourrons reprendre plus bas grâce à une autre forme d'équation réduite.
Soient donc, ordonnées selon les y croissants, les deux courbes:
avec deg(A) ≤ 3; deg(B) ≤ 2; etc...Dorénavant, nous enlèverons les "(x)" quand ils n'apportent rien au calcul.
Résolvante-express
On va essayer de se ramener à la seule chose que l'on sache bien faire:
la résolution d'un système linéaire
Le quadruplet (1, y , y2 , y3 ) vérifie deux équations... voilà qui n'est pas très carré!
Mais il vérifia aussi, par exemple, celle que l'on déduit de la seconde en la multipliant par y.
On a donc
Chaque fois qu'il y a un point d'intersection, il y a un y tel que le système ait une solution non triviale: son déterminant est nul, c'est un polynôme en x (la résolvante) puisqu'il se calcule par somme et produit de A, B, C, D, a, b, c; il convient de vérifier que son degré est inférieur ou égal à 2 x 3, d°f x d°F en général; cela vient du fait que les degrés sont en progrssion arithmétique dans chaque ligne (chaque terme du dét a un seul élément par ligne et colonne).
La méthode d'Euler et Bézout
La présence d'un facteur commun à f et F se traduit par
l'écriture
On écrit ces polynômes à coefficients indéterminés, ici
On reporte dnas la relation , et on identifie les puissances de y ; l'écrire en "semi-développé" permet de rapprocher de la manière précédente tout en préparant l'identification:
On retrouve, à transposition près, la matrice précédente pour le système aux inconnues r, s, u, v w ; il admet une solution si et seulement si le déterminant est nul (puisque le système est homogène). L'extension aux degrés quelconques se laisse imaginer facilement.
Cependant, il ne pourrait y avoir plus de d°f ordonnées pour une racine de la résolvante; cela prouve déjà que l'intersection a un nombre fini k de points, à partir desquels on forme k.(k-1)/2 droites. À l'exception de celles-ci, aucune droite ne peut contenir deux points d'intersection des courbes; il y a donc toujours moyen de choisir une direction pour l'axe des y qui vérifie cette condition; dès lors à une abcisse d'intersection ne correspont qu'un point d'intersection.
Il est à noter que cette remarque apparaît explicitement dans le traité de Cramer (voir ci-dessous).
Brève Histoire du Théorème
Il est probable qu'en manipulant les exemples, comme nous venons
de le faire -déférence gardée envers les maîtres- les mathématiciens
ont eu très tôt l'intuition du résultat. Ce "ressenti" doit donc être
presque aussi vieux que la Géomètrie
de Descartes (1637) qui fonde la Géométrie Algébrique. Ceux qui en
douteraient trouveront matière à conviction dans la préface d'un
ouvrage
essentiel pour la gestation d'une preuve :
Tout seigneur, tout honneur, Newton l'emploie, comme une évidence dès 1665; il donnera en 1707 des calculs délimination complets pour deux polynômes de degré 2,, et 4: quand on vous disait qu'il n'est pas déshonorant de regarder comment ça marche sur les plus bas degrés: si Newton le fait, on peut bien suivre son exemple sans déshonneur, non?
Aux Temps pré-Bézoutiens
Deux figures se détachent particulièrement dans la revendication d'une
preuve, celles de MacLaurin, puis de Cramer. Mais on ne sait rien de ce
qu'a fait le premier, et les efforts du second ne sont exempts ni de
lourdeurs (notamment dans les notations), ni de passages obscurs.
De Cramer, Bézout retiendra particulièrement l'étude des systèmes linéaires, pour lequel l'histoire a surtout retenu son nom (en particulier les fameuses formules dont les étudiants fontsi mauvais usage, tant elles sont impraticables d'un point de vue caalculatoire, surtout par un ordinateur). Mais c'est là que s'introduisent les déterminants (eh oui, bien avant les matrices, contrairement à l'ordre pédagogique contemporain!) et Bézout saura tirer parti de cet outil des systèmes linéaires pour un problème a priori hors du champ de la linéarité!
Entre MacLaurin et Cramer, il convient de citer l'inévitable Euler -inévitable, parce qu'il y a peu de sujets de son temps qui échappent à son appétit d'ogre mathématique... Il a d'ailleurs beaucoup correspondu avec Cramer, sur ce sujet et bien d'autres concernant la géométrie des courbes. Le chapitre XIX, De l'Intersection des Courbes de Introduction à l'Analyse Infinitésimale, t.2, donne surtout les calculs systématiques d'élimination jusqu'au degré 4, et attire l'attention sur les solutions imaginaires (voir l'exemple que nous en avons tiré au début). Voyons comment il travaille
Méthode 1 d'Euler:
Il l'expose sur un exemple "pour mieux la faire voir", mais sa généralité est claire. Il s'agit d'abaisser le degré en y, en substituant aux deux équations d'origine, deux nouvelles équations, chacune ayant un degré diminué de 1: un algorithme s'en dégage par réitération, jusquà ce que, parvenu à la forme
La manière mérite qu'on s'y arrête. Sans surprise, faire une combinaison linéaire (à coefficients fonctions de x) compense les termes de plus haut degré (les y4 dans l'exemple): c'est l'équation IV de son texte. Plus original, il compense les termes constants, puis divise par y, ce qui le mène à III.
Selon John Stillwell, cette méthode était
déjà connue des
mathématiciens chinois au XIIème siècle, et fut même adaptée à 4
inconnues en 103 par Zhu Shijié dans un ouvrage au nom très poétique, Le Miroir de Jade des quatre Inconnues
(Siyuan yujian). On attend encore en Occident un traité
d'algèbre dont le seul nom fasse autant rêver...
Méthode 2 d'Euler:
C'est la méthode des coefficients indéterminés, que nous avons présentée plus haut. Mais Euler ne la fait guère apparaître comme la résolution d'un système linéaire.
N.B. : Le mot même de déterminant viendra plus tard, avec Gauss (1801), la notation qui nous est familière du tableau entre deux barres aussi, et, même s'il y a de quoi surprendre l'étudiant de première année à qui l'on présente rituellement les matrices puis les déterminants, les matrices attendront un demi-siècle de plus pour être ainsi nommées et utilisées en petites tailles par Sylvester (1850), Cayley (1854); le cas n x n ne sera guère abordé avant Frobenius (1898), c'est à dire la fin d'un siècle qui accouche de l'algèbre linéaire dans la douleur, ou, tout au moins, la lenteur... pour ne rien dire de son enseignement et de son utilisation en physique, pour lesquels il faudra laisser passer deux guerres: un physicien de l'envergure d'Heisenberg était fort mal à l'aise avec la non commutativité du produit matriciel!
L'ordre choisi (avec raison) pour le confort pédagogique n'a que peu à voir avec l'ordre historique d'apparition des concepts, et le cas de l'Algèbre Linéaire est particulièrement frappant. Ce qui démontre, par l'exemple, l'intérêt d'un retour en arrière, une fois l'acquisition technique réalisée.
Vous pourrez suivre Bézout pas à pas, dans ces articles, cette vidéo... et ce livre!
Exemples à 4x2 = 8 points
EX 11 : la besace (ainsi se trouve bien nommée cette courbe de degré 4) et le cercle ont d'abord deux points d'intersections réels simples qui sont bien en évidence. Qu'en estil en O? Chacun des deux arcs de la besace est tangent au cercle; autrement dit: chacun des deux arcs a, avec le cercle, un contact d'ordre 2. Cela représente un contact d'ordre 4 pour les deux courbes, et c'est ce que confirmerait l'utilisation d'un paramétrage rationnel du cercle (obtenu par y=tx); ou encore, reporter un DL d'ordre 2 du cercle y = βx² + o(x² ) le montre très rapidement.
2 + 4 = 6, il manque encore deux points pour faire un bon compte! Eh bien, ils sont à la fois à l'infini et complexes, car, passant en coordonnées homogènes x = X/T , y = Y/T, on trouve "à l'infiini":
Les courbes ont donc en commun les points I (1, i, 0 ) et J (1, -i, 0 ) ; ce sont les célèbres "points cycliques", qui tirent leur nom du fait que tous les cercles les contiennent. Et cette fois, le compte y est: 2 + 4 +2 = 8.
EX 12 : au lieu d'être un cercle tangent quelconque, celui-ci est le cercle de courbure en O à l'arc le plus proche de y=0 de la besace. Il a un contact d'ordre 3 au moins avec le cercle, qui monte nécessairement à 4 en raison de la symétrie! L'ordre du contact en O pour les deux courbes est donc 4+2 =6, et les points I et J subsitent.
Avec... un peu moins de gesticulation mais un peu (à peine!) plus de calculs, le report du DL local du cercle : y = βx² + o(x² ) fournira aisément l'équation
qui montre que le contact est en général d'ordre 4, sauf pour deux valeurs où il monte à 6; la plus grande est celle de cet exemple...
EX 13 : et la deuxième correspond au cercle de courbure de l'arc "supérieur", beaucoup plus serré!
EX 14 : La quartique est la célébre lemniscate de Bernoulli. O est à compter deux fois (tout se passe comme si chaque arc de la lemniscate coupait le cercle en un point simple); deux autres points sont complexes, et tout cela se vérfie aisément en prenant un paramétrage rationnel du cercle, exactement comme dans l'exemple 12. Et il ne peut y en avoir d'autres à distance finie, car l'équation résolvante est de degré 4 (et non 8!). Les 4 autres sont à l'infini, ce sont I (1, i, 0 ) et J (1, -i, 0 ) rencontrés ci-dessus, mais cette fois chacun est point double de l'intersection. Non par un contact, mais parce que I et J sont des points doubles de la lemniscate
Ce sont des nœuds, cest à dire que l'allure locale est similaire à celle en O de la cubique de l'ex.6.
EX 15 : la seule modification concerne l'existence d'un point de contact réel, donc double de l'intersection. En diminuant encore le coefficient de x et y, on obtiendrait deux points réels simples. Le cas tangent est "frontière" entre ce dernier et le cas où ils sont imaginaires, comme dans l'ex. 14
EX 16 : Rien ne change à l'infini, où I et J demeurent chacun point double de l'intersection, car ce sont les mêmes équations qu'en 14 et 15
EX 17 : le bifolium ne ressemble que de loin à la besace de l'ex. 12! Il y a deux raisons à cela: ses points à l'infini vérifient
ce ne sont donc PAS ceux du cercle: il n'y a plus d'intersection à l'infini! Par ailleurs, l'origine, point double pour la besace (tout se passant comme s'il y avait deux arcs à point simple) est maintenant faite localement d'un arc simple, tangent à y=0, et d'un arc à point double O dont la tangente est x=0 (dissociez le en pensée, il ressemble à x2 = y3 ), en sorte que l'origine est point triple du bifolium.
L'intersection réelle comprend deux points réels simples, et O quadruple (double par contact avec le sous-arc tangent à y=0, double avec le sous-arc tangent à x=0 parce que O en est point double). Il reste deux points imaginaires, et tout ceci se vérifie par le calcul en paramétrant le bifolium (couper par une sécante au point triple, y=tx).
EX 18 : O demeure quadruple , mais d'une façon différente: 4=1+3 (simple avec le sous-arc tangent à y=0, triple avec le sous-arc tangent à x=0 parce que O en est point double: le "modèle" local de cette deuxième intersection est
EX 17 bis: essayez donc cet autre bifolium :
Un seul terme change dans l'équation, et la courbe réelle qu'on peut dessiner a une allure vraiment similaire! Pourtant, on retrouve nos amis I et J dans l'intersection, puisqu'à l'infini
Ce sont des points simples du bifolium , et de l'intersection. (Sans entrer dans le détail, la différence avec l'ex.14 peut ne pas sauter aux yeux; elle tient à la différence de degré entre les termes dominants et les suivants, 2 pour la lemniscate et 1 = 4-3 ici; en homogénéisant l'équation, un T apparaît au lieu d'un T2)
EX 19 : En chacun des rebroussements de l'astroïde, la situation est, localement, celle de l'ex.4, c'est à dire une multiplicité 2 de l'intersection; voilà donx déjà 4x2 = 8 points de l'intersection. I et J sont, de façon évidente, sur l'astroïde comme sur le cercle, mais -c'est moins immédiat à l'œil nu!- ce sont aussi des rebroussements! Autrement dit, la position relative du cercle et de l'astroïde en I et J ne diffère pas de celle des 4 rebroussements réels, fonurnissant les 2x2 = 4 points qui manquaient à notre décompte.
EX 20 : En deux rebroussements de l'astroïde, la situation est, localement, identique à celle de l'ex.5, la multiplicité de l'intersection est 3. La situation en I et J reste la même que dans l'ex. 18, et l'on a ainsi en récapitulant
Construire vos Exemples Personnels à m x n points ?
N'hésitez pas à aller puiser de belles courbes dans le très complet
catalogue conçu par Robert Ferréol: vous y trouverez les
figures, avce leurs équations, de quoi vous inspirer des situations
originales!
Entre Enfer et Paradis
Revenons pour conclure à un cas simple, mais qui peut questionner, du théorème "fort": où sont les quatre points d'intersection de deux cercles concentriques?
Avant de répondre, observons que Dante se fait une représentation très
classique (à son époque) du Cosmos géocentrique. Et n'oublion pas qu'un des premiers diagrammes de Copernic est lui aussi fait de cercles concentriques -aux choix du centre près!
Références
Historiques
Complémentaires
Revenir
à la Home
Page du
MathouristePetits rappels: un monôme en deux variables x, y a pour degré la somme des degrés en x et y; par exemple x3 y2 est de degré 5. Le degré d'un polynôme est le plus grand degré de ses monômes; une courbe algébrique l'ensemble des points du plan où il s'annule: P (x, y) = 0.
Le Théorème de Bézout existe en deux versions:
| faible |
FORTE |
| Deux courbes algébriques de degrés m et n se coupent en m.n points au plus. |
Deux courbes algébriques de degrés m et n se coupent en m.n points exactement. |
Commençons par un avis d'expert:
| "
J'ai rapporté sans
démonstration cette proposition, que
deux lignes courbes
algébriques, dont l'une est
de l'ordre m et l'autre de l'ordre n, se peuvent
couper en m.n points.
La vérité de cette
proposition est reconnue de tous les géomètres,
quoiqu'on doive avouer, qu'on n'en trouve
nulle part une démonstration assez rigoureuse. Il y a des vérités générales que notre
esprit est prêt d'embrasser aussitôt qu'il en
reconnaît la justesse dans quelques cas particuliers
: et c'est parmi cette espèce de vérités
qu'on peut ranger à bon droit la proposition,
dont je viens de faire mention, puisqu'on la trouve vraie non seulement dans
quelques ou plusieurs cas, mais aussi dans une infinité de cas différents.
Cependant on
conviendra aisément que toutes ces preuves infinies
ne sont pas capables de mettre cette
proposition à l'abri de toutes les objections
qu'un adversaire peut former, et qu'il faut
absolument une démonstration rigoureuse, pour le réduire au silence." L. Euler, Démonstration sur le nombre de points où
deux lignes quelconques peuvent se couper
Académie des Sciences de Berlin, 1748 |
Approche par les exemples
Faisons donc comme les successeurs, ou pour le dire à sa manière, comme les Neveux de Descartes: promenons nous dans le jardin des courbes, observons, et... apprenons à compter les intersections, ce qui est un peu plus subtil qu'on ne pourrait croire au premier coup d'œil!Une cubique, un cercle
Une cubique, rappelons le, est une courbe dont les points annulent un polynôme en x et y de degré 3. Le cercle est, quant à lui, un cas particulier de conique, c'est à dire de degré 2. En combien de points peuvent-elles se rencontrer? Comment les déterminer par le calcul? Voici quelques configurations, qui ne sont pas exhaustives.Notre dernière ligne donne le nombre de points d'intersection "ressentis". Eh oui, comme avec les prévisions météo, dans les problèmes d'intersection, il y a le mesuré et le ressenti!
Les exemples proposés ont été choisis pour éviter des calculs trop compliqués. En particulier, former l'équation aux abcisses des intersections (résolvante) se fait par simple report dans tous les cas sauf un, où l'on gagne en deux coups.
EX 1 : l'équation résolvante est x2 + ( x3 - 4 x )2 - x - 8 = 0, soit
x6 - 8 x4 +
17 x2 - x - 8
= 0
Elle n'a rien de très souriant, bien sûr, mais nous pouvons confier à une machine sa résolution numérique et confirmer qu'elle a 6 racines. L'appartion du degré 6 résulte simplement de la substitution d'un terme de degré 3 en x de la cubique dans un terme carré de la conique.
EX 2 : l'équation résolvante est :
x3 +
x2 - 4
= 0
Elle n'a qu'une seule racine réeelle, entre 1 et 2, comme l'étude des variations le montre élémentairement. Sa positivité permet de trouver deux solutions en y correspondantes, il n'y a donc que deux points réeels d'intersection.
EX 3 : l'équation résolvante est
x3 +
x2 - 2x + 0.4 = 0
Elle a déjà deux racines positives,
l'une entre 0 et 1/2, l'autre entre 1/2 et 1, ce que l'on voit en
prenant les valeurs en 0, 1/2 et 1 du polynôme au premier membre. Elles
donnent naissance aux 4 points que l'on voit. Mais ayant deux racines
réelles, notre polynôme en a nécessairement une troisième, nommons la α , qu'on peut situer
rapidement entre -3 et -2 par le changement de signe. Elle est donc négative, et par suite il ne lui
correspond aucune ordonnée y
telle que y2 = α3
< 0.
Pour ceux qui auraient la curiosité de lire l'argument dans son
jus d'origine... il n'y a plus qu'à agrandir!
| N.B. : Ce type de situation n'a pas échappé au grand Euler, qui donne l'exemple, encore plus simple d'une parabole et d'un cercle. Le discours, lui, est un peu plus alambiqué, comme s'il avait des scrupules à parler de nombres complexes, lui qui est rompu à leur emploi. Peut-être veut-il , en multipliant les précautions oratoires, ne pas alarmer outre mesure un lecteur qui éprouverait de la gêne à voir surgir des points imaginaires sur les courbes bien réelles qui sont l'objet de la géométrie traditionnelle. | ||
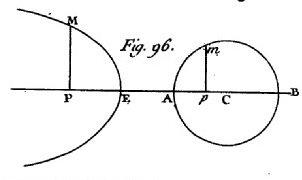
| La parabole a pour équation : y2
=
2ax - 2ab Le cercle e a pour équation : y2 = -2cx - x2 a, b, c, sont positifs ; "pour que nous soyions bien assurés qu'il n'y a aucun point d'intersection", b est la distance AE. du sommet de la parabole à l'extrémité d'un diamètre. Euler oriente l'axe vers la gauche -nos coutumes ont changé!- et nomme apppliquée l'ordonnée. L'équation résolvante est x2 + 2 ( a + c ) x -2ab = 0, qui a deux racines réeelles (leur produit est négatif) mais le report conduit à égaler y2 à un négatif. Il n'a plus qu'à conclure: |
 |
|
|
||
 |
 |
 |
|
| la figure dans sa planche |
Euler, Introduction à l'Analyse
Infinitésimale, t2, chapitre XIX |
||
On comprend dès ce moment que l'étude va inévitablement rencontrer la question du nombre de racines d'un plunôme de degré n. C'est donc sans doute le bon endroit pour rappeler deux faits importants, qu'il convient de ne pas mélanger, car le premier est élémentaire, et le second beaucoup moins.
TH A : un polynôme de degré n a au plus n racines.
TH B (théorème fondamental de l'Algèbre, dit aussi de d'Alembert-Gauss) : un polynôme de degré n a exactement n racines, dans le corps des complexes.
Le premier résulte de la divisibilité par X - α lorsque α est racine, et de la théorie du degré. Le second n'est pas démontré à l'époque de Bézout, même s'il est largement pressenti. Et inexorablement, l'étude des courbes algébriques va glisser vers le domaine complexe au siècle suivant, pour pouvoir énoncer des résultats généraux.
Mais revenons à nos exemples.
EX 4 : l'équation résolvante est :
x3 +
x2 - 2 x = x ( x - 1)
( x +
2 ) = 0
On trouve les points (1,-1), (1, 1), (0,0). Mais le dernier est à compter deux fois, car
pour x = 0
, l'équation qui détermine l'ordonnée est y2 = 0, qui possède une racine double
en 0. Si l'on compare à l'ex. 3, tout se
passe comme si les deux points
d'intersection de gauche venaient se fondre en un seul en 0.
On peut d'ailleurs, si on le souhaite, faire tous les calculs en
prenant un cercle mobile qui se rapproche de l'origine: x2 + y2 -
2 x + ε = 0
et l'on verra vraiment le cas actuel devenir la limite du
pécédent.On obtient en tout, avec ce premier exemple de multiplicité d'une intersection, 4 points réels (et deux imaginaires supplémentaires, pour arriver à 6 en tout)
EX 5 : l'équation résolvante s'obtient cette fois en deux temps. On remplace l'expression du cercle par le report de y2 tiré de la seconde:
x3 +
x2 - 2
y = 0
& y2 = x3
(conserver
l'équation reportée
est une méthode simple et sûre pour garantir que l'on peut faire le
chemin inverse vers le système précédent; on a transformé le système en
un système équivalent, donc on n'a ni rajouté ni perdu de solutions, ce
qui est le risque principal dans ce genre de calculs...)Cela a abaissé le degré en y de la première (on voit ainsi se dessiner une méthode systématique), qui permetd'expliciter y et de reporter dans la seconde. le degré 6 de la résolvante s'explique bien par 3x2.
x3 +
x2 - 2
y = 0
& ( x3 +
x2)2
= 4 x3
soit la résolvante x6 + 2 x5 + x4 - 4 x3 = x3 ( x - 1)
( x2 + 3 x + 4) = 0
Cette fois, 0 est racine triple, pourquoi?
Parce qu'en plus de la rencontre en un point douvble de la cubique, les
deux courbes ont même
tangente: elles partagent un ordre de contact supplémentaire.
L'intersection est encore composée de 4 points réels, (1,1) et (0,0) compté 3
fois. S'y ajoutent deux imaginaires, car l'équation
restante en x est sans racines réelles.EX 6 : l'équation résolvante s'obtient de nouveau par simple report, et elle est de degré 3; c'est un effet de la symétrie mutuelle des deux courbes (pas de terme en y, donc pas de deuxième étape de report):
x3 + 4 x2 + 3 x = x ( x + 1)
( x +
3 ) = 0
Deux phénomènes bien distincts apparaissent.- En x =-3, le report donne y2 = 0 , (-3,0) est à compter deux fois parce que les deux courbes sont tangentes: une rencontre simple, en se coupant transversalement, donne une racine simple, mais partager la même tangente donne un ordre de contact supplémentaire (comme on le constate sur un développement limité pour deux fonctions f(x) et g(x) par exemple.)
- En x =0, le report donne y2 = 0 , (0,0) est à compter deux fois. Toutefois le phénomène est bien différent: la cubique possède un point double, avec deux tangentes différentes à deux arcs différents. Le cercle rencontre chacun de ces deux arcs "de manière simple"... et 1+1 = 2.
Une hyperbole, une parabole... et une excursion lointaine
Les exemples précédents ont fait ressentir la nécessité de prendre en
compte, si l'on veut espérer un dénombrement exact donné par le produit
des degrés, l'existence de points imaginaires et les divers aspects de
la multiplicité. Ce n'est pourtant encore pas tout, comme le prouvera
l'exemple ci-dessous. | EX 7 xy + y - x = ( x - 1).( y - 1) - 1 = 0 y= x2 |
Avec
deux coniques, on peut attendre qu'un bon
décompte trouve 2 x 2 = 4 points d'intersection dans tous les cas; or,
considérons:
Son degré est 3, elle a 3 racines réelles... alors qu'on se serait attendu au degré 4 avec 0,2 ou 4 racines selon leur réalité. Où est passé le quatrièmepoint? sera-t-on tenté de dire. Eh bien, il est... à l'infini, dans la direction x = 0, qui est direction asymptotique commune aux deux courbes. Ces idées peuvent être mises en forme très rigoureusement, mais il faut avoir recours à la Géométrie Projective inventée par Jean-Victor Poncelet. On a alors recours aux coordonnées homogènes x = X/T , y = Y/T
|
En résumé, pour avoir un théorème de Bézout "fort" (le nombre de points d'intersection de deux courbes algébriques est égal au produit de leurs degrés), il faut accepter les points imaginaires, les points à l'infini, et les multiplicités, soit d'un point sur une courbe, soit de l'intersection si les courbes ont un contact "plus proche" (par ex. être tangentes correspond à une multiplicité 2). La simplicité du résultat est à ce prix... les mathématiciens n'ont pas compliqué par plaisir; ils ont été poussé à considérer les courbes dans ces espaces ambiants plus grands que le plan usuel pour continuer à travailler efficacement et produire des résultats.
Le démontrer en basse dimension ?
L'idée peut vous paraître saugrenue; historiquement, elle ne l'est pas
tant que cela, comme on le verra. Deux droites (degré 1 et 1):
Deux droites d'équations a x + b y +
c = 0 et u x + v y + w = 0
se coupent en un point unique... sauf si elles sont parallèles. Mais en
ce cas, elles partagent la même direction (-b,a). Dans les coordonnées
homogènes de la géométrie projective,
x = X/T, y = Y/T, ces
droites ont pour équationsa X
+ b Y + c T = 0 et u X + v Y
+ w T = 0
et elles partagent le point (-b,a,0).
Deux coniques (degré 2 et 2):
Méthode 1 : utiliser l'équation réduite d'une des deux coniquesEn choisisant un repère adapté, la première peut-être mise en forme "semi-réduite" y2 = a x2+ b x + c = Q(x) -que nous appelons ainsi parce que cest la première étape vers les formes réduites en repère quelconque. La seconde aura la forme la plus générale
A x2+ 2B xy + C y2
+
2D x + 2E y + F = C y2
+
P1(x) y + P2(x) = 0
en l'ordonnant en y; l'indice du ploynôme en x indique son degré maximal. Comme dans l'EX 5, l'élimination de y se conduit en deux temps: un premier report fait disparaître les y2 de la seconde, abaissant son degré à 1; dans un second temps le report de l'expression rationnelle en x obtenue pour y fournira la résolvante en x:
y2 = a x2+ b x + c = Q(x) & [ C Q(x) + P2(x) ] + P1(x) y = 0
puis P1(x)2 Q(x) - [ C Q(x) + P2(x) ]2
= 0 &
y = - [ C Q(x) + P2(x) ] / P1(x)
C'est la méthode d'abaissement du degré. Comme on l'a déjà indiqué, la tactique consistant à conserver celle des deux équations que l'on reporte dans l'autre est simple et sûre pour éviter tout ajout de solution parasite. L'équation obtenue est clairement de degré inférieur ou égal à 4, sans que l'on puisse dire plus, car on soustrait deux termes de degré inférieur ou égal à 4. Voici une description d'époque du procédé, par un illustre auteur, responsable des articles scientifiques de l'ouvrage:
| " EVANOUIR n. (Algebre) On dit que l'on fait évanoüir une inconnue d'une
équation, quand on la fait disparoître de cette équation, en y
substituant la valeur de cette inconnue. Voyez EQUATION. Quand il y a plusieurs inconnues dans un problème, une des difficultés de la solution consiste à faire évanoüir les inconnues, qui empêchent de reconnoître la nature & le degré de ce problème. [...] Quand il arrive que dans aucune des deux équations, la quantité inconnue n'est d'une seule dimension, il faut trouver dans chaque équation la valeur de la plus grande puissance de cette inconnue ; & si ces puissances ne sont pas les mêmes, on multipliera l'équation qui contient la plus petite puissance de cette inconnue par la quantité que l'on se propose de faire évanoüir, ou par son quarré ou son cube, &c. jusqu'à ce que cette quantité ait la même puissance qu'elle a dans l'autre équation : après quoi l'on fait une équation des valeurs de ces puissances ; d'où résulte une nouvelle équation, dans laquelle la plus haute puissance de la quantité que l'on veut faire évanoüir, est diminuée de quelque degré, & en répétant une pareille opération, l'on fera évanoüir enfin cette quantité." d'Alembert, L'Encyclopédie (le lien renvoie à
l'article complet sur le site
de l'Encyclopédie en ligne)
|
Exercice: le calcul est encore moins volumineux à partir d'une des formes réduites y2 = x , y2 - x2 = 1 , y2 - x2 = 1, mais il faut s'y reprendre à trois fois...
Méthode 2 : utiliser un paramétrage pour une des deux coniques
C'est une situation idéale pour étudier une intersection que de disposer d'une courbe sous forme paramétrée et de l'autre en cartésiennes, car l'étude de l'intersection dse fait par simple report. Prenons pour origine un point sur la première conique, et coupons par une sécante variable issue de ce point:
a x2+
2b xy + c y2
+
2d x + 2e y = 0
& y = tx
Après avoir enlevé le facteur x
(prévisible puisque le point (0,0) est sur la courbe), il reste x ( a +
2b t + c t2)
= - 2 ( d + e t
) ; y = tx
soit x = Q1(t) / Q2(t) ; y = t Q1(t) / Q2(t)
autrement dit, x et y sont des fractions rationnelles en t dont les degrés du numérateur et du dénominateur n'excèdent pas 2, et, point extrêment important, le dénominateur est le même pour les deux ; c'est de là que vient le fait que le degré de l'équation aux paramètres t de l'intersection ne dépassera pas 4; c'est, après avoir chassé les dénominateurs
A Q1(t)2+ 2B t Q1(t)2+ C t2Q1(t)2+ 2D Q1(t)Q2(t) + 2E t Q1(t)Q2(t) + F Q2(t)2
= 0
C'est une somme de 6 termes dont aucun n'a un degré qui dépasse 4.
Méthode 3 : se ramener à un cas plus facile
Avec un simple report, on règle le cas d'une conique et d'une droite: deux points d'intersection au plus, deux exactement en admettant points imaginaires ou points à l'infini. Si l'on considère le cas trivial où l'une des deux coniques est décomposée en deux droites, le résultat est aussi simple que... 2 x 2 = 4. Peut-on s'y ramener?
Le système des deux équations qui définit l'intersection des deux coniques est
f (x, y) = 0 & g (x, y) = 0
et il est équivalent pour tout λ à celui-ci f (x, y) = 0 & λ f (x, y) + g (x, y) = 0
La question est alors naturelle: peut-on trouver un tel que la deuxième soit une coniques décomposée en deux droites? Il est facile de voir que cela revient à ce que cette conique possède un point double. Un petit calcul auxiliaire donne pour cela une équation du trosième degré en λ, ce qui assure qu'uelle aura au moins une racine réelle, et l'affaire sera encore résolue!
Encore des exemples!
Juste pour se rappeler que multiplicités et rencontres à l'infini demeureront de la partie.
Voici d'abord une ellipse et un cercle, passant tous deux par O... et un autre point à coordonnées positives (cliquer sur les images zoomées pour mieux voir!). Sans calcul: il est évident que l'ellipse et le cercle ont même tangente x - 2y = 0 , donc O est au moins point double... mais que voit-on si l'on effectue un petit développement limité des deux fonctions donnant localement y en fonction de x ? (pas besoin d'être un savant connaisseur du théorème des fonctions implicites: il est évident qu'on peut donner des formules explicites, tellement moches qu'on ne les explicitera surtout pas:! Mais cela ne les empêche pas de garantir existence et régularité de ces fonctions, on peut alors calculer les développements par coefficients indéterminés)
On prouvera ce que nos yeux voient : leur différence est d'ordre 3: les deux courbes se traversent en changeant de position relative; le cercle est au dessus de l'ellipse à gauche de O, en dessous à droite. Les 4 points d'intersection sont réeels, O est triple.
| EX 8 | EX 8, zoom 1 | EX 8, zoom 2 |
| |
||
|
x2 + xy + y2 + x - 2y = 0 et x2
+ y2 + 2 α x
-4 α y = 0
; α = 5/14
|
||
Votre serviteur a utilisé le cercle de courbure de l'ellipse au point considéré; il est parmi les cercles tangents à l'ellipse le seul à avoir un contact d'ordre au moins (et, ici, exactement) 3; on peut du reste facilement voir que tout autre cercle tangent ( contact d'ordre 2) reste, soit intérieur, soit extérieur à l'ellipse en O.
Allons maintenant à l'infini, voir ce qui s'y passe...
| EX 9 |
EX 10 |
|
xy
- x2 + 2x - 2y -1/10
= 0
xy = 1
|
xy - x2 + 2x - 1/10 = 0
xy = 1
|
| 4 points, dont un à l'infini |
4 points, dont deux à l'infini |
Dans l'EX 9, les deux hyperboles ont trois points réels d'intersection; le dernier, à l'infini, représente la direction asymptotique commune x = 0. Les asymptotes respectives, x = 0 et x = 2, sont distintres.
Dans l'EX 10, les deux hyperboles ont deux points réels d'intersection; le dernier, à l'infini, représente toujours la direction asymptotique commune x = 0. Mais il est double, car les courbes ont cette fois la même asymptote x = 0, situation comparable à la propriété d'avoir même tangente à distance finie.
On remarque immédiatement (simple report de y = 1/x que la résolvante aux abcisses est de degré 3 = 4-1 pour le premier (un point à l'infini), 2 = 4-2 pour le second (un point double à l'infini)
N.B. : nous avons ici déterminé l'intersection de deux coniques en résolvant une équation du quatrième degré (en général). Mais "travailler en sens inverse" a aussi son intérêt: ramener la résolution d'une équation algébrique à l'intersection de deux coniques. C'est ce qu'a proposé le grand mathématicien persan Omar al-Khayyam (1048-1131) pour résoudre les équations du troisième degré: il ajoute la racine"factice" 0 en multipliant par x, et construit deux coniques, les plus simples possibles, dont les abbcisses d'intersection sont 0 et les racines de la proposée. Nous vous en reparlerons bientôt dans une page spéciale!
Deux cubiques (degré 3 et 3):
Pourquoi ne pas essayer les mêmes idées? Mais pas forcément dans le même ordre!Méthode 2 : utiliser un paramétrage d'une des deux cubiques
On l'a dit plus haut, c'est idéal pour étudier une intersection que de disposer d'une courbe sous forme paramétrée et de l'autre en cartésiennes... et cela n'a rien à voir avec le degré! Avec pour l'une d'elles
x = P(t) / R(t) ; y = Q(t) / R(t)
(*)
P, Q, R étant des polynômes de degré inférieur ou égal à 3 pour représenter l'une, avec le même dénominateur R; et l'autre sous sa forme la plus générale
f (x, y) = [ A x3+ B x2y + C xy2
+ D y3
]+ [ E x2 + 2F xy + G y2
] + H x + K y + L = 0
ou encore, en groupant par degrés homogènes (selon les crochets):f (x, y) = f3 (x,
y) + f2 (x,
y) +f1 (x,
y) +L = 0
le report donnera une équation en t de degré inférieur ou égal à 3 x 3 = 9; il n'est guère besoin d'explicitertout pour s'en convaincre. Le seul point important est que c'est le même dénominateur R3que l'on chasse pour retrouver une équation polynômiale.
Tout irait pour le mieux dans le meilleur des mondes si toute cubique admettait un paramétrage rationnel... mais ce n'est pas le cas!
En fait, un paramétrage rationnel ne tient que pour les cubiques à point double. Si on place l'origine en un tel point de g (x, y) = g3 (x, y) + g2 (x, y) +g1 (x, y) +L' = 0, la constante est nulle; et si ne l'est pas, la courbe a une disposition d'arc régulier dont la tangente est g1 (x, y) = 0. Coupant par y = tx on a (si vous ne le voyez pas sous cette forme résumée, développez ces expressions)
x2
[ x g3 (1, t) + g2 (1, t) ] = 0 ; y = tx
d'où la forme attendue. Cela, c'est la partie facile; il faut un peu plus de travail pour montrer qu'en l'absence de point double, pas de paramétrage rationnel... et cela n'avancerait guère notre propos.
Méthode 1 : utiliser l'équation réduite d'une des deux cubiques
Sans nous interroger sur son origine, provisoirement au moins, admettons qu'un bon choix de repère nous donne, pour la première, une forme "semi-réduite", qui apparait assez proche de celle des conqieus rencontrée précédemment, à savoir
y2 = a x3+ bx2
+ cx + d = Q(x)
. La seconde reste sous la
forme la plus
générale
f (x, y) = [ A x3+ B x2y + C xy2
+ D y3
]+ [ E x2 + 2F xy + G y2
] + H x + K y + L = 0
ou encore, ordonnée en y (
en ne traitant que le cas où D
est non nul; c'est encore plus simple sinon) :y3
+ y2 P1(x) + y P2(x) + P3(x) = 0
l'indice marrquant encore pour les polynômes,ici et dans la suite, le
degré maximum.y2 = Q(x) & [ Q(x) + P2(x) ] y + [ P3(x) + Q(x) P1(x) ] = 0
puis y2
= Q(x) & y = - R4(x) / R3(x)
La résolvante sera
R3(x)2 Q(x) + R4(x)2
= 0
Le premier terme est de degré inférieur ou égal à 9 = 2 x 3 + 3 ,
le second à 8, donc inférieur ou égal à 9 pour la somme.Revenons maintenant sur le lemme utilisé... et son illustre auteur:
| "Les cubiques représentées par l'équation y2 = a x3+ bx2
+ cx + d (1)
[...]sont comprises entre les cubiques
nommées paraboles divergentes par Newton dans son Enumeratio
linearul tertii ordinis.
Ces courbes jouent un rôle important dans la théorie générale des
cubiques, à cause de ce beau théorème, donné par le grand géomètre dans
l'ouvrage cité:
l'équation (1) peut représenter
la perspective de toutes les cubiques.
On ne
sait pas quelle voie a été suivie par Newton pour obtenir cette
intéressante propriété, car il n'en a pas publié la
dmonstration. Cette démonstration a été donnée plus tard par Clairaut et Nicole, en 1731, dans les
Mémoires de l'Académie des Sciences de Paris."
F. Gomes-Teixeira, Traité des Courbes Spéciales
Remarquables, t. 1
|
 |
|
| Le Maître en personne, chez lui, à
Trinity College (Cambridge) |
brouillon autographe de Newton |
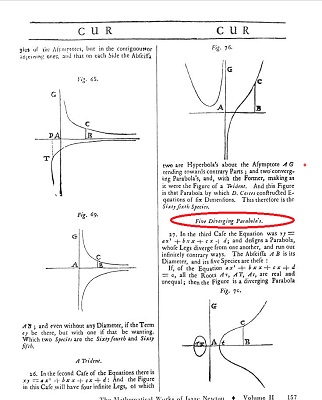
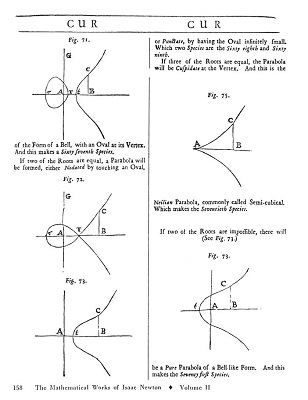
Voici, dans la traduction anglaise (l'original est en latin), les deux pages où Newton présente les 5 formes de paraboles divergentes, et celle de son affirmation, que nous traduisosns en Français.
 |
 |
 |
| "Si l'on projette, sur un plan infini, les Ombres des Figures depuis un point
lumineux, les ombres des Sections Coniques seront toujours des Sections Coniques [...]; et les Ombres des
courbes du Troisième Ordre sront elles-mêmes de cet Ordre, et ainsi ad
infinitum. Et de même qu'un Cercle, par ombre projetée,
engendre toutes les Sections Coniques,
les cinq Paraboles divergentes dont on a parlé au §27 engendreront par
leur ombre, et feront voir, toutes les Courbes du Troisième Ordre;
quant aux Courbes d'Ordres supérieurs, on pourra de même encore trouver
certaines Courbes plus simples du même Ordre, qui, par projection
depuis un point lumineux, les engendrent." |
||
Oui, MAIS !!!!
Comment prouve-t-on, le plus généralement, ce résultat sur lequel nous nous appuyons? Écrire qu'un point est d'inflexion -c'est à dire que la tangente y a un ordre de contact avec la courbe, au moins égal à 3 (et donc égal, dans le cas d'une cubique!) mène (élémentairement, sans théorie génrale sur la Hessienne) à situer le point sur une autre courbe du troisième degré... et à conclure, par le théorème de Bézout, que les deux ont neufs points en commun, donc nécessairement, un au moins réel.
Et nous venons donc de fabriquer un magnifique cercle vicieux!!!
Moralité
intéressante : toujours être prudent dans l'utilisation d'un résultat
admis.
La converture de l'ouvrage de Stirling reproduit, en image, le Sheldonian théâtre de l'Université d' Oxford ! |
Si James
Stirling reprend, commente, illustre, voire complète le traité du
maître, il n'apporte pas de démonstration sur ce résultat,ni sur
la question du nombre de points d'une intersection, que Newton tient
pour une évidence. |
|
 |
"Cest à l'Illustre Mr. NEWTON que la Géométrie est est surtout redevable de cette distribution. Son Énumération des Lignes du troisième Ordre est un excellent modèle de ce qu'il faut faire en ce genre, & une preuve convaincante que ce grand Homme avoit pénétré jusqu'au fonds de ce que la Théorie des Courbes a de plus delié & de plus intéressant. Il est fâcheux que Mr. NEWTON se soit contenté d'étaler ses découvertes sans y joindre les Démonstrations, & qu'il ait préféré le plaisir de se faire admirer à celui d'instruire. [...] Mr STIRLING a développé les Principes & la Méthode de Mr NEWTON , dans l'excellent Commentaire qu'il nous a donné sur son Livre. On y voit qu'il ne manquoit presque rien à Mr STIRLING pour donner une Théorie complète des Courbes, & qu'il n'auroit laissé que peu de choses à dire, s'il ne s'étoit pas attaché avec trop de scrupule à ne point s'écarter de son Auteur." G.
Cramer, Introduction à l'Analyse des
Lignes Courbes (1750)
|
|
Les preuves de Clairaut et Nicole évoquées ci-dessus par Gomes-Teixeira (et que mentionne aussi Cramer) semblent exemptes de cette perfide circularité, mais la contrepartie est la longueur des calculs (et la typographie de l'époque n'en rend pas la présentation très agréable...). on se fera une opinion en les consultant sur Gallica (BnF) : Clairaut (pp 483-493) et Nicole (pp 494-511, 3 planches hors pagination à la suite) les deux se trouvent l'un derrière l'autre dans le recueil de l'Académie.
 |
 |
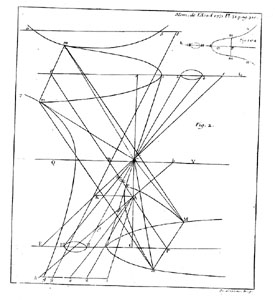 |
| premières pages des mémoires de Clairaut
et Nicole |
figure de Nicole |
|
mais patience... nous pourrons reprendre plus bas grâce à une autre forme d'équation réduite.
Un Aperçu de Méthode Générale... sur un Exemple
Il est clair qu'on ne peut aller guère plus loin par les procédés employés antérieurement, dont le seul mérite était de faire voir comment le degré montait. Ce que nous allons proposer maintenant peut être fait à tous les degrés, mais en le voyant sur le cas d'une cubique et une conique, nous éviterons les manipulations d'indices qui peuvent être rébarvbatives pour le débutant.
Soient donc, ordonnées selon les y croissants, les deux courbes:
F(y) = A(x) +
B(x) y + C(x) y2
+ D(x) y3 = 0
f(y) = a(x) + b(x) y + c(x) y2 = 0
f(y) = a(x) + b(x) y + c(x) y2 = 0
avec deg(A) ≤ 3; deg(B) ≤ 2; etc...Dorénavant, nous enlèverons les "(x)" quand ils n'apportent rien au calcul.
Résolvante-express
On va essayer de se ramener à la seule chose que l'on sache bien faire:
la résolution d'un système linéaireLe quadruplet (1, y , y2 , y3 ) vérifie deux équations... voilà qui n'est pas très carré!
A 1
+ B y + C y2 + D y3 = 0
a 1 + b y + c y2 = 0
a 1 + b y + c y2 = 0
Mais il vérifia aussi, par exemple, celle que l'on déduit de la seconde en la multipliant par y.
a y + b y2
+
c y3 = 0
On peut faire de même avec la première, mais apparaît alors un y4 ;
le quadruplet devient quintuplet... ajouter une équation ajoute une
inconnue! Il faut donc doser soigneusement le moment de l'arrêt. Or, si
l'on multiplis la première par 1, y , la
seconde par 1, y , y2 ,
cela conduira à éfcrire 2 + 3 = d°f + d°F
équations en 5 inconnues homogènes, l'idéal pour avoir, quand
tout va bien, une solution unique à un facteur près. Plus
profondément, dela correspond au produit de F par un
polynôme de degré d°f - 1et de f par un
polynôme de degré d°F - 1, le bon ajustement pour traduire
l'existence d'un facteur commun (ce qu'on verra au § suivant).On a donc
| A 1
+ B y + C y2
+ D y3
= 0 A y + B y2 + C y3 + D y4 = 0 a 1 + b y + c y2 = 0 a y + b y2 + c y3 = 0 a y2 + b y3 + c y4 = 0 |
Chaque fois qu'il y a un point d'intersection, il y a un y tel que le système ait une solution non triviale: son déterminant est nul, c'est un polynôme en x (la résolvante) puisqu'il se calcule par somme et produit de A, B, C, D, a, b, c; il convient de vérifier que son degré est inférieur ou égal à 2 x 3, d°f x d°F en général; cela vient du fait que les degrés sont en progrssion arithmétique dans chaque ligne (chaque terme du dét a un seul élément par ligne et colonne).
La méthode d'Euler et Bézout
La présence d'un facteur commun à f et F se traduit par
l'écriture f = Q
g et F
= Q G
d'où g F + (-G) f = 0 ; d°(g)
≤ d°f - 1 & d°(G)
≤ d°F - 1
On écrit ces polynômes à coefficients indéterminés, ici
g(y) = r + s y
; -G(y) = u + v y
+ w y2
On reporte dnas la relation , et on identifie les puissances de y ; l'écrire en "semi-développé" permet de rapprocher de la manière précédente tout en préparant l'identification:
r F + s y F +
u f + v y f +
w y2 f = 0
|
r A + r B y + r C y2
+ r D y3 + s A y + s B y2 + s C y3 + s D y4 + u a + u b y + u c y2 + v a y + v b y2 + v c y3 + w a y2 + w b y3 + w c y4 = 0 |
soit |
r
A + u a
= 0 (en
y0 ) r B + s A + u b + v a = 0 (en y1 ) r C + s B + u c + v b + w a = 0 (en y2 ) r D + s C + v c + w b = 0 (en y3 ) s D + w c = 0 (en y4 ) |
On retrouve, à transposition près, la matrice précédente pour le système aux inconnues r, s, u, v w ; il admet une solution si et seulement si le déterminant est nul (puisque le système est homogène). L'extension aux degrés quelconques se laisse imaginer facilement.
Remarque: fin de la preuve du théorème de Bézout "faible"
Comme on n'a pas éliminé pas à pas, on ne dispose pas à la fin d'un y = .... (rationnel en x) à reporter. Chaque verticale tracée à partir d'une racine pourrait fort bien couper chaque courbe eb plusieurs points; ainsi avoir d°f x d°F abcisses pour racines de la résolvante ne gearantit pas le même nombre de points; il pourrait même y en avoir plus!Cependant, il ne pourrait y avoir plus de d°f ordonnées pour une racine de la résolvante; cela prouve déjà que l'intersection a un nombre fini k de points, à partir desquels on forme k.(k-1)/2 droites. À l'exception de celles-ci, aucune droite ne peut contenir deux points d'intersection des courbes; il y a donc toujours moyen de choisir une direction pour l'axe des y qui vérifie cette condition; dès lors à une abcisse d'intersection ne correspont qu'un point d'intersection.
Il est à noter que cette remarque apparaît explicitement dans le traité de Cramer (voir ci-dessous).
Brève Histoire du Théorème
Il est probable qu'en manipulant les exemples, comme nous venons
de le faire -déférence gardée envers les maîtres- les mathématiciens
ont eu très tôt l'intuition du résultat. Ce "ressenti" doit donc être
presque aussi vieux que la Géomètrie
de Descartes (1637) qui fonde la Géométrie Algébrique. Ceux qui en
douteraient trouveront matière à conviction dans la préface d'un
ouvrage
essentiel pour la gestation d'une preuve :| "C'est
surtout dans la Théorie des Courbes qu'on éprouve sensiblement
l'utilité d'une Méthode aussi générale que l'est celle de l'Algèbre. DES
CARTES, dont l'esprit inventeur ne brille pas moins dans la Géométrie
que dans la Philosophie, n'eut pas plutôt introduit la manière
d'exprimer la nature des Courbes par des équations algébriques, que
cette Théorie changea de face. Les découvertes se multiplièrent
avec une extraordinaire facilité: chaque ligne de Calcul enfantoit de
nouveaux Théorèmes. Part ce moyen, l'art supplée au génie, & le
génie aié d'un art si secourable a eu des succès qu'il n'auroit jamais
obtenu par ses propres forces." G. Cramer, Introduction à l'Analyse des Lignes
Courbes (1750)
|
Tout seigneur, tout honneur, Newton l'emploie, comme une évidence dès 1665; il donnera en 1707 des calculs délimination complets pour deux polynômes de degré 2,, et 4: quand on vous disait qu'il n'est pas déshonorant de regarder comment ça marche sur les plus bas degrés: si Newton le fait, on peut bien suivre son exemple sans déshonneur, non?
Aux Temps pré-Bézoutiens
Deux figures se détachent particulièrement dans la revendication d'une
preuve, celles de MacLaurin, puis de Cramer. Mais on ne sait rien de ce
qu'a fait le premier, et les efforts du second ne sont exempts ni de
lourdeurs (notamment dans les notations), ni de passages obscurs. |
"
Je vous suis très obligé de m'avoir informé du fait que certains
papiers ont été communiqués à la [Royal] Society sur ce sujet auquel je
me suis particulièrment attaché d_ès ma prime jeunesse. Qu'on ait eu le
soin de le faire il y a environ qutre ans m'aurait évité une très
désagrable dispute. [...] Vous savez, Monsieur, qu'en 1721 j'ai fait imprimer près de quatre feuilles de Supplément à mon Traité sur la Description des Lignes Courbes. Ce traitté a été écrit alors que j'étais très jeune et imprimé alors que je navais pas 21 ans. J'avais alors pensé en différer plusieurs fois la publication; mais diverse raisons me poussaient à l'envoyer à l'étranger.[...] Bien conscient qu'il était incomplet sur plusieurs points, je revins sur le sujet à l'été 1720, et de nouveau à celui de 1721 où j'ai préparé un Supplément consistant en deux parties. Dans la première, je démontrais de façon générale que que deux Lignes, l'une d'ordre m et l'autre d'ordre n, se coupent en un nombre de points égal à mn, c'est à dire le produit des ordres de ces Lignes." Colin MacLaurin, lettre à [probablement John Machin], 1731
lettre 137 in The Collected Letters of Colin MacLaurin (S. Mills ed) |
 |
| [Préface] "Le troisième Chapitre développe la division des Lignes algébriques selon leurs différents Ordres. On y voit les Équations générales de chacun de ces Ordres, le nombre de leurs termes [...] & le nombre des Points donnés par lesquels une Ligne d'un Ordre donné peut rencontrer une Ligne du même Ordre, ou d'un autre Ordre aussi donné. La Règle qui détermine ce nombre est très importante dans la Théorie des Courbes, plusieurs grands Géomètres l'ont supposée, mais personne, que je sache, n'en a donné la Démonstration. On la prouve ici, par une manière, expliquée dans l'Appendice, N°2, de faire évanouir une grandeur indéterminée, au moyen de deux Équations dans lesqeulles elle entre. C'est là proprement un Problème de pure Algèbre; mais les Méthodes connues ayant paru insuffisantes, on a cherché une autre, qui rend la chose facile [...]" |
 |
|
[ch III, §42] "Alors, si l'on fait s'évanouir x ou y par le moyen des équations des deux Lignes, il restera une équation, qui aura au moins autant de racines qu'il y a de points de rencontre des deux Lignes. [...] Or, il est démontré* que si l'on a deux variables, & deux équations indéterminées qui expriment le raport [sic] de ces variables avec des constantes, desquelles l'une soit de l'ordre m et l'autre de l'ordre n ; lors qu'au moyen de ces deux équations on chasse une de ces variables, celle qui reste n'a, dans l'équation finale qui la détermine, que mn dimensions sau plus. Elle ne peut donc avoir,dans cette équation, que mn racines au plus. Par conséquent, deux Lignes algébriques décrites sur un même plan, ne peuvent se rencontrer qu'en autant de points , au plus, qu'il n'y a d'unités dans le produit des nombres qui sont les exposants de leurs Ordres. ** [Notes] * Ce Principe, purement algébrique, devroit être démontré dans l'Algèbre. Comme je n'en connois aucune qui en donne la Délonstration, j'ai crû devoir l'insérer dans l'Appendice, N°3. **Mr MAC-LAURIN a démontré la même chose, mais je ne crois pas que la démonstration ait été rendue publique." G. Cramer, Introduction à l'Analyse des Lignes
Courbes (1750)
|
 |
|
De Cramer, Bézout retiendra particulièrement l'étude des systèmes linéaires, pour lequel l'histoire a surtout retenu son nom (en particulier les fameuses formules dont les étudiants fontsi mauvais usage, tant elles sont impraticables d'un point de vue caalculatoire, surtout par un ordinateur). Mais c'est là que s'introduisent les déterminants (eh oui, bien avant les matrices, contrairement à l'ordre pédagogique contemporain!) et Bézout saura tirer parti de cet outil des systèmes linéaires pour un problème a priori hors du champ de la linéarité!
Entre MacLaurin et Cramer, il convient de citer l'inévitable Euler -inévitable, parce qu'il y a peu de sujets de son temps qui échappent à son appétit d'ogre mathématique... Il a d'ailleurs beaucoup correspondu avec Cramer, sur ce sujet et bien d'autres concernant la géométrie des courbes. Le chapitre XIX, De l'Intersection des Courbes de Introduction à l'Analyse Infinitésimale, t.2, donne surtout les calculs systématiques d'élimination jusqu'au degré 4, et attire l'attention sur les solutions imaginaires (voir l'exemple que nous en avons tiré au début). Voyons comment il travaille
Méthode 1 d'Euler:
Il l'expose sur un exemple "pour mieux la faire voir", mais sa généralité est claire. Il s'agit d'abaisser le degré en y, en substituant aux deux équations d'origine, deux nouvelles équations, chacune ayant un degré diminué de 1: un algorithme s'en dégage par réitération, jusquà ce que, parvenu à la forme
A(x) +
B(x) y = 0 & a(x) + b(x) y = 0
la dernière élimination lui fournisse la résolvante A(x) b(x) - B(x) a(x) = 0
La manière mérite qu'on s'y arrête. Sans surprise, faire une combinaison linéaire (à coefficients fonctions de x) compense les termes de plus haut degré (les y4 dans l'exemple): c'est l'équation IV de son texte. Plus original, il compense les termes constants, puis divise par y, ce qui le mène à III.
7 |
 |
| Application: retour sur l'Intersection de
deux Cubiques N.B. : pour chaque polynôme, l'indice désignera aussi le degré maximum de ce polynôme. Avec un choix un peu moins contraignant (faire en sorte que la droite de l'infini Z=0 soit une tangente à la courbe -et non plus une tangente d'inflexion, c'est beaucoup plus banal! Puis prendre pour X=0 la tangente au point où Z=0 recoupe la courbe), on peut réduire la première cubique à x y2 + (ax + b) y = c x2 + d x +
e soit x y2 + P1(x)
y - P2(x) = 0
la seconde étant sous la forme généraley3
+ y2 Q1(x) + y Q2(x) + Q3(x) = 0
On commence par une demi-étape puisque la première est de degré 2: on
la multiplie par -y et la
seconde par x pour obtenir,
en ajoutant l'élimination des y3 (x Q1- P1) y2 + (x Q2
+
P2) y + Q3(x) = 0
soit le système, abaissé au degré 2 en y
x y2 + P1 y - P2
= 0
On fait maintenant deux combinaisons: R2 y2 + R3 y + Q3 = 0 - d'abord en multipliant la première par -R2 et la seconde par x ; -ensuite, en multipliant la première par Q3 et la seconde par P2 ;
(x R3 - P1 R2 ) y + (x Q3 + P2 R2 ) = 0
(x Q3 + P2 R2 ) y2 + (P1 Q3 + P2 R3 ) y = 0 Enfin, on divise la seconde par y pour parvenir à la forme
S4 y + T4 = 0
et nous voilà à la résultante, qui culmine par son premier terme au
degré 9 = 5+5U4 y + V5 = 0
S4 V5 -U4 T4 = 0
Ce qui établit le résultat général sur les cubiques, sans avoir besoin d'envoyer une inflexion à l'infini! N.B. : Retour au texte de Newton: ce qu'il aurait pu faire... Lorsqu'il attaque sa classsification des Cubiques, en discutant suivant la partie homogène dominante (de degré ), Newton les répartit en 4 familles en adaptant son repère:
|
Méthode 2 d'Euler:
 |
 |
C'est la méthode des coefficients indéterminés, que nous avons présentée plus haut. Mais Euler ne la fait guère apparaître comme la résolution d'un système linéaire.
Mais comment Bézout s'y prenait-il?
S'il part du même système à coefficients indéterminés qu'Euler, il a sur lui l'avantage de travailler avec un système homogène et surtout de traduire l'existence d'une solution par l'annulation du déterminant qu'on appellera plus tard résultant. L'idée de déterminant, prise chez Cramer, est bien plus claire avec Bézout, qui donne le premier, de façon très explicite, la règle de développement suivant une colonne pour construire les déterminants d'ordre à partir de ceux d'ordre 2, etc... |
 |
| Ici, Bézout donne le calcul du déterminant
en énumérant toutes les permutations possibles, dûment signées; c'est ce qu'il a hérité de Cramer. |
Après quoi, pour avoir un caclul "moins
pénible", il propose ce qui
correspond à un développement par
rapport à la dernière colonne: c'est son innovation personnelle! |
N.B. : Le mot même de déterminant viendra plus tard, avec Gauss (1801), la notation qui nous est familière du tableau entre deux barres aussi, et, même s'il y a de quoi surprendre l'étudiant de première année à qui l'on présente rituellement les matrices puis les déterminants, les matrices attendront un demi-siècle de plus pour être ainsi nommées et utilisées en petites tailles par Sylvester (1850), Cayley (1854); le cas n x n ne sera guère abordé avant Frobenius (1898), c'est à dire la fin d'un siècle qui accouche de l'algèbre linéaire dans la douleur, ou, tout au moins, la lenteur... pour ne rien dire de son enseignement et de son utilisation en physique, pour lesquels il faudra laisser passer deux guerres: un physicien de l'envergure d'Heisenberg était fort mal à l'aise avec la non commutativité du produit matriciel!
L'ordre choisi (avec raison) pour le confort pédagogique n'a que peu à voir avec l'ordre historique d'apparition des concepts, et le cas de l'Algèbre Linéaire est particulièrement frappant. Ce qui démontre, par l'exemple, l'intérêt d'un retour en arrière, une fois l'acquisition technique réalisée.
Vous pourrez suivre Bézout pas à pas, dans ces articles, cette vidéo... et ce livre!
|
 |
Et après...
Dans le cadre d'un enseignement exemplairement moderne, Laplace n'hésite pas à le mentionner dans sa 6ème Leçon à l'École Normale de l'An III, le 21 Ventôse (11 Mars 1795). C'est toutefois plus un survol rapide et une indication bibliographique qu'un cours minutieux sur le sujet; après avoir évoqué l'élimination à la manière de d'Alembert, il ajoute:| "Vous
trouverez cette méthode exposée dans un grand détail et
appliquée à un
nombre quelconque d'équations et d'inconnues dans un très bon ouvrage
de Bézout qui a pour titre: Théorie des Équations. L'auteur y démontre,
par une application ingénieuse du calcul aux différences finies, ce
théorème général, savoir que, si
l'on a un nombre quelconque
d'équations complètes entre un pareil nombre l'inconnues, le degré de
l'équation finale, résultant de l'élimination de toutes les inconnues, à l'exception d'une seule, est
égal au produit des degrés de toutes ces équations." [souligné par Laplace lui-même] |
Encore des Exemples pour le Théorème "Fort"
Nous savons mainteant, même si nous ne l'avons pas prouvé ici, que le nombre de points de l'intersection est le produit des degrés, à condition de compter les multiplicités, les points imaginaires, et les points à l'infini (qui peuvent aussi être imaginaires, ou multiples, ou les deux à la fois).Saurez-vous
les trouver tous dans les images suivantes?
Exemples à 4x2 = 8 points
| x2 (x2+ y2 ) - 4 x2 y + y2 = 0 et x2 + y2 - 2 α y = 0 | ||
| EX 11 | EX 12 | EX 13 |
| α = 1,5 | 2 α = 2 + √ 3 = 3.732 ... | 2 α = 2 - √
3 = 0.268 ... |
EX 11 : la besace (ainsi se trouve bien nommée cette courbe de degré 4) et le cercle ont d'abord deux points d'intersections réels simples qui sont bien en évidence. Qu'en estil en O? Chacun des deux arcs de la besace est tangent au cercle; autrement dit: chacun des deux arcs a, avec le cercle, un contact d'ordre 2. Cela représente un contact d'ordre 4 pour les deux courbes, et c'est ce que confirmerait l'utilisation d'un paramétrage rationnel du cercle (obtenu par y=tx); ou encore, reporter un DL d'ordre 2 du cercle y = βx² + o(x² ) le montre très rapidement.
2 + 4 = 6, il manque encore deux points pour faire un bon compte! Eh bien, ils sont à la fois à l'infini et complexes, car, passant en coordonnées homogènes x = X/T , y = Y/T, on trouve "à l'infiini":
T = 0 , X2 ( X2+ Y2 ) = 0 et X2+ Y2 = 0
Les courbes ont donc en commun les points I (1, i, 0 ) et J (1, -i, 0 ) ; ce sont les célèbres "points cycliques", qui tirent leur nom du fait que tous les cercles les contiennent. Et cette fois, le compte y est: 2 + 4 +2 = 8.
EX 12 : au lieu d'être un cercle tangent quelconque, celui-ci est le cercle de courbure en O à l'arc le plus proche de y=0 de la besace. Il a un contact d'ordre 3 au moins avec le cercle, qui monte nécessairement à 4 en raison de la symétrie! L'ordre du contact en O pour les deux courbes est donc 4+2 =6, et les points I et J subsitent.
Avec... un peu moins de gesticulation mais un peu (à peine!) plus de calculs, le report du DL local du cercle : y = βx² + o(x² ) fournira aisément l'équation
[ β2 x2
+ (β2 - 4 β + 1) y ] x4
= 0
qui montre que le contact est en général d'ordre 4, sauf pour deux valeurs où il monte à 6; la plus grande est celle de cet exemple...
EX 13 : et la deuxième correspond au cercle de courbure de l'arc "supérieur", beaucoup plus serré!
| EX 14 | EX 15 | EX 16 |
| |
||
| (x2+ y2 )2 - x y = 0 x2 + y2 - 0.8 x - 0.8 y = 0 |
(x2+ y2 )2 - x y = 0 x2 + y2 - 0.5 x - 0.5 y = 0 |
(x2+ y2 )2 - x y = 0 x2 + y2 - y = 0 |
EX 14 : La quartique est la célébre lemniscate de Bernoulli. O est à compter deux fois (tout se passe comme si chaque arc de la lemniscate coupait le cercle en un point simple); deux autres points sont complexes, et tout cela se vérfie aisément en prenant un paramétrage rationnel du cercle, exactement comme dans l'exemple 12. Et il ne peut y en avoir d'autres à distance finie, car l'équation résolvante est de degré 4 (et non 8!). Les 4 autres sont à l'infini, ce sont I (1, i, 0 ) et J (1, -i, 0 ) rencontrés ci-dessus, mais cette fois chacun est point double de l'intersection. Non par un contact, mais parce que I et J sont des points doubles de la lemniscate
T = 0 , ( X2+ Y2 )2 = 0
Ce sont des nœuds, cest à dire que l'allure locale est similaire à celle en O de la cubique de l'ex.6.
EX 15 : la seule modification concerne l'existence d'un point de contact réel, donc double de l'intersection. En diminuant encore le coefficient de x et y, on obtiendrait deux points réels simples. Le cas tangent est "frontière" entre ce dernier et le cas où ils sont imaginaires, comme dans l'ex. 14
EX 16 : Rien ne change à l'infini, où I et J demeurent chacun point double de l'intersection, car ce sont les mêmes équations qu'en 14 et 15
T = 0 , ( X2+ Y2 )2 = 0 , X2+ Y2 = 0
Il y a un point réel simple, reste donc 8 - (2 + 2 +1) = 3 points...
tous en O , car des deux
sous-arcs locaux de la lemniscate, celui qui est tangent à x=0 a une intersection simple avec
le cercle, tandis que l'autre partage avec le cercle la même tangente y=0, ce qui en fait un point double
de l'intersection: O a donc 3 pour multiplicité d'intersection.
| EX 17 |
EX 18 |
| |
|
| x4+ y4 - 4 x2 y = 0 x2 + y2 - 2 y = 0 |
x4+ y4 - 4 x2 y = 0 x2 + y2 - 3 x = 0 |
EX 17 : le bifolium ne ressemble que de loin à la besace de l'ex. 12! Il y a deux raisons à cela: ses points à l'infini vérifient
T = 0 , X4+ Y4 = 0
ce ne sont donc PAS ceux du cercle: il n'y a plus d'intersection à l'infini! Par ailleurs, l'origine, point double pour la besace (tout se passant comme s'il y avait deux arcs à point simple) est maintenant faite localement d'un arc simple, tangent à y=0, et d'un arc à point double O dont la tangente est x=0 (dissociez le en pensée, il ressemble à x2 = y3 ), en sorte que l'origine est point triple du bifolium.
L'intersection réelle comprend deux points réels simples, et O quadruple (double par contact avec le sous-arc tangent à y=0, double avec le sous-arc tangent à x=0 parce que O en est point double). Il reste deux points imaginaires, et tout ceci se vérifie par le calcul en paramétrant le bifolium (couper par une sécante au point triple, y=tx).
EX 18 : O demeure quadruple , mais d'une façon différente: 4=1+3 (simple avec le sous-arc tangent à y=0, triple avec le sous-arc tangent à x=0 parce que O en est point double: le "modèle" local de cette deuxième intersection est
x2 = y3
, y = x2
pour qui l'ordre 3de O se
voit immédiatement (reporter la deuxième dans la première).EX 17 bis: essayez donc cet autre bifolium :
(x2+ y2)2 - 4 x2 y = 0 = x4+ 2 x2y2 + y4 - 4 x2 y
Un seul terme change dans l'équation, et la courbe réelle qu'on peut dessiner a une allure vraiment similaire! Pourtant, on retrouve nos amis I et J dans l'intersection, puisqu'à l'infini
T = 0 , ( X2+ Y2 )2 = 0 et X2+ Y2 = 0
Ce sont des points simples du bifolium , et de l'intersection. (Sans entrer dans le détail, la différence avec l'ex.14 peut ne pas sauter aux yeux; elle tient à la différence de degré entre les termes dominants et les suivants, 2 pour la lemniscate et 1 = 4-3 ici; en homogénéisant l'équation, un T apparaît au lieu d'un T2)
Exemples à 6 x 2 = 12 points
| EX 19 | EX 20 |
| |
|
|
(x2+ y2 - 1)3 + 27 x2 y2 = 0
x2 + y2 - 2 α y = 0
|
(x2+ y2 - 1)3 + 27 x2 y2 = 0 x2 + y2 - 2 x - 2 y = 0 |
EX 19 : En chacun des rebroussements de l'astroïde, la situation est, localement, celle de l'ex.4, c'est à dire une multiplicité 2 de l'intersection; voilà donx déjà 4x2 = 8 points de l'intersection. I et J sont, de façon évidente, sur l'astroïde comme sur le cercle, mais -c'est moins immédiat à l'œil nu!- ce sont aussi des rebroussements! Autrement dit, la position relative du cercle et de l'astroïde en I et J ne diffère pas de celle des 4 rebroussements réels, fonurnissant les 2x2 = 4 points qui manquaient à notre décompte.
EX 20 : En deux rebroussements de l'astroïde, la situation est, localement, identique à celle de l'ex.5, la multiplicité de l'intersection est 3. La situation en I et J reste la même que dans l'ex. 18, et l'on a ainsi en récapitulant
3 x 2 + 2 x 2 = 10 points.
Les deux derniers points sont imaginaires, ce que peut révéler un
paramétrages rationnel du cercle.Construire vos Exemples Personnels à m x n points ?
N'hésitez pas à aller puiser de belles courbes dans le très complet
catalogue conçu par Robert Ferréol: vous y trouverez les
figures, avce leurs équations, de quoi vous inspirer des situations
originales!Une Belle Application
Le théorème est utilisé, entre autres, dans une preuve du théorème de l'hexagramme mystique de Pascal, la preuve n°4 de notre page dédiée à ce beau résultat: ne manquez pas d'aller la voir en suivant le lien! Car si la figure se trouve dans beaucoup de livres, peut-être la verrez vous pour la première fois gravée dans la pierre! On n'a besoin que de cas très simples, car il s'agit d'intersection de deux cubiques particulières, réunions de trois droites ou d'une droite et une conique, entièrement démontrés ici.Entre Enfer et Paradis
Revenons pour conclure à un cas simple, mais qui peut questionner, du théorème "fort": où sont les quatre points d'intersection de deux cercles concentriques? | Maison de Dante Florence (Italie) |
Cercles du Paradis de Dante, par Massimo Tosi (Mason de Dante) |
Boticelli, le cercle de Mercure
illustration pour le livre de Dante |
La Divine Comédie couverture, d'après une gravure de Gustave Doré. |
 Lady Macbeth de Mzesk (Dmitri Chostakovitch) mise en scène à lOpéra Bastille, 2019 |
à gauche, le décompte est facile: deux points d'intersection réeels, et, n'oublions pas, les fameux points cycliques I (1, i, 0 ) et J (1, -i, 0 )puisque tous les cercles les contiennent
à droite, .ils sont toujours communs à deux cercles. Alors, où sont les deux autres? En I (1, i, 0 ) et J encore, car ce soints chacun des points doubles de l'intersection: des cercles concentriques sont tangents à l'infini!
Cela conforte l'intuition qu'ils ont en commun quelque chose de plus spécial que deux cercles en position quelconque, que cela fait la différence entre les deux images de droitye et de gauche.Ah, qu'il fait de belles choses, l'imaginaire, à l'infini.....
|
 LA figure de Copernic |
Références
Historiques
- É. BÉZOUT, Recherches sur le degré des équations résultantes de l'évanouissement des inconnues et sur les moyens qu'il convient d'employer pour trouver ces équations
- É. BÉZOUT, Théorie Générale des Équations Algébriques (sur e|rara, ETH Zürich)
- G. CRAMER, Introduction à l'Analyse des Lignes courbes algébriques (sur e|rara, ETH Zürich)
- L. EULER, Introduction à l'Analyse Infinitésimale, tome 2 (sur Gallica-BnF)
- C. MACLAURIN, Geometria Organica (sur Google-Books)
- J. STIRLING, Lineae Tertii Ordinis Neutonianae (sur Google-Books)
Complémentaires
- A. ASH, R. GROSS, Elliptic Tales (Princeton)
- R.BIX, Conics and Cubics, A Concrete Introduction to Algebraic Geometry (Springer)
- E. BRIESKORN, H. KNÖRRER, Plane Algebraic Curves (Birkhaüser)
- J. COOLIDGE, A Treatise on Plane Algebraic Curves (Dover)
- G. FISCHER, Plane Algebraic Curves (Alerican Math. Society, Student Texts vol. 15)
- C.J. GIBSON, Elementary Geometric Algebraic Curves, An Undergraduate Introduction (Cambridge University Press)
- H. HILTON, Plane Algebraic Curves (Oxford University Press)
- F. KIRWAN, Complex Algebraic Curves (London Math. Society, Student Texts 23)
- E. KUNZ, Introduction to Plane Algebraic Curves (Birkhaüser)
- M. REID, Undergraduate Algebraic Geometry (London Math. Society, Student Texts 12)
- G. SALMON, A treatise on the Higher Plane Curves (sur Google-Books)
- J. STILLWELL, Mathematics and its History (Springer)
