Une Promenade dans l'Irrationnel

• Les épisodes disponibles de la série! Chacun est autonome et peut être lu indépendamment des autres.
  
• #1  La promenade commentée "à travers la longue histoire" de la question,  sous forme du diaporama (en .pdf) de la conférence;
• #2  L'outil merveilleux de l'irrationalité: les Fractions continuées, dans une approche douce ;
  
• #3  L'étude du nombre e, presque tout... avec les moyens du programme de Terminale! (la page est désormais complète, avec images et liens).
  
  
• Des (extraits de) textes originaux choisis, pouvant être étudiés et commentés avec des lycéens.
• Platon, sur la duplication du cube (Ménon);
• Klein sur la caractérisation des irrationnels constructibles;
  
• Klein sur le problème de Délos et la trisection de l'angle;
• Klein sur la dénombrabilité des nombres algébriques;
• Lagrange sur les fractions continuées et leur application à la résolution des équations.

• La bibliographie complète. (ci-dessous)

• Des compléments, textes, images, commentaires, sont à retrouver dans les pages de ce site (toutes ne sont pas achevées); vous pouvez utilement consulter celles consacrées aux héros croisés en chemin: Pythagore, Al-Khowarizmi, Al-Biruni, Al-Khayyam (à créer prochainement), Al-Kashi, Huygens, Euler, Lambert, Lagrange, Fourier, Segner, Hermite, ou aux lieux évoqués (Darb-e-Imam à Isfahan pour les pavages apériodiques, théâtre d'Epidaure pour les fractions continues).

• Enfin, n'oubliez pas le site BibNum qui présente une riche collection de textes originaux accompagnés d'un commentaire de lecture: une aide pour vous, mais aussi des idées sur la façon de créer cet accompagnement; loin d'être unique, elle est propre à chaque contributeur... de quoi vous faire votre propre idée, en fonction du public ciblé, sur la manière dont vous conduirez le vôtre! La théorie des nombres et les questions d'irrationalité y sont bien représentées.

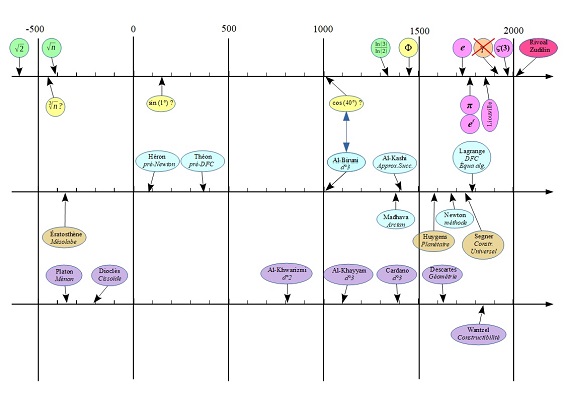Un synoptique de l'Irrationalité... à agrandir en cliquant!

Bibliographie abrégée (Les Indispensables!)

1. Le Petit Archimède, n° Spécial Pi, Revue du Palais de la Découverte, 1980. (réédition ADCS)
2. J. AYMES, Ces Problèmes qui font les Mathématiques: la Trisection de l'Angle. (Brochure APMEP n°70)
3. J.-L. CHABERT & al. , Histoire d'Algorithmes (Belin)
4. J.P. DELAHAYE, Le Fascinant Nombre Pi (Belin)
5. J. HAVIL, The  IrratiΦnals (Princeton University Press)
6. F. KLEIN, Leçons sur certaines Questions de Géométrie Élémentaire (Diderot)
7. H. LEBESGUE, Leçons sur les Constructions Géométriques (Gautheirs-Villars, réédition J. Gabay)
8. E. MAOR, The Pythagorean Theorem (Princeton University Press)
9. P. NAHIN, An Imaginery Tale: the Story of i (Princeton University Press)
10. M. NEVEUX / H.E. HUNTLEY, Le Nombre d'Or / La Divine Proportion (Points Sciences )
11. I. NIVEN, Irrational Numbers (Wiley)
12. B. RITTAUD, Le Fabuleux destin de racine carrée de deux (Ed. du Pommier)

1. J. HAVIL, The  IrratiΦnals (Princeton University Press)
2. F. KLEIN, Leçons sur certaines Questions de Géométrie Élémentaire (Diderot)
3. B. RITTAUD, Le Fabuleux Destin de Racine Carrée de Deux (Ed. du Pommier)
4. J. AYMES, Ces Problèmes qui font les Mathématiques: la Trisection de l'Angle. (Brochure APMEP n°70)
5. Le Petit Archimède, n° Spécial Pi, Revue du Palais de la Découverte, 1980. (réédition ADCS)
6. M. NEVEUX / H.E. HUNTLEY, Le Nombre d'Or / La Divine Proportion (Points Sciences)
7. J.-L. CHABERT & al. , Histoire d'Algorithmes (Belin)
8. H. BOAULEM, R. BROUZET, La Planète R (Dunod)
9. H. LEBESGUE, Leçons sur les Constructions Géométriques (Gauthiers-Villars, réédition J. Gabay)
10. I. NIVEN, Irrational Numbers (Wiley)
11. P. NAHIN, An Imaginery Tale: the Story of i (Princeton University Press)
12. E. MAOR, The Pythagorean Theorem (Princeton University Press)

Bibliographie générale

Textes historiques (Sources Premières)

• R. DESCARTES, La Géométrie
• L. EULER, les Archives EULER: bientôt, tout Euler en ligne!
• M. GHYKA, Le Nombre d'Or (Gallimard)
• M. GHYKA, The Geometry of Art and Life (Dover)
• C. HERMITE, OEUVRES COMPLETES
  
• Oeuvres, tome 1 (à l'Université du Michigan)
• Oeuvres, tome 2 (à l'Université du Michigan)
• Oeuvres, tome 3 (à l'Université du Michigan) 
  
• Oeuvres, tome 4 (à l'Université du Michigan)
• H. HELMHOLTZ, Théorie Physiologique de la Musique (Masson)
• E. HOBSON, Squaring the Circle : a History of the Problem (Cambridge, en ligne à l'Université du Michigan )
• F. KLEIN, Leçons sur certaines Questions de Géométrie Élémentaire (Diderot)
• J. LAMBERT, l’irrationalité de π (1761)  sur le site BibNum .
• H. LEBESGUE, Leçons sur les Constructions Géométriques (Gautheirs-Villars, réédition J. Gabay)
• J. LIOUVILLE, Sur des Classes très étendues de Quantités dont la valeur n'est ni Rationnelle... (CRAS , 15 mai 1844)
  
• C. MACMAURIN, Traité d'Algèbre, et de la Manière de l'Appliquer  (GoogleBooks)
• M. MERSENNE, L'Harmonie Universelle  (Gallica BnF)
• J.-E. MONTUCLA, Histoire des Recherches sur la Quadrature du Cercle  (Bachelier, en ligne sur Gallica BnF)

Ouvrages accessibles (niveau *, Élèves)

• Le Petit Archimède, n° Spécial Pi, Revue du Palais de la Découverte, 1980. (réédition ADCS)
• E. BARBIN, A. BOYE, , François Viète (Vuibert)
• J.-L. CHABERT & al. , Histoire d'Algorithmes (Belin)
• J.P. DELAHAYE, Le Fascinant Nombre Pi (Belin)
• D. FLANNERY, The Square Root of 2 (Copernicus Books)
• P. HEMENGWAY, Le Code Secret (Evergreen)
• M. NEVEUX / H.E. HUNTLEY, Le Nombre d'Or / La Divine Proportion (Points Sciences )

Ouvrages de Références (niveau **, Profs)

• J. AYMES, Ces Problèmes qui font les Mathématiques: la Trisection de l'Angle. (Brochure APMEP n°70)
• A. ASH, R.GROSS, Elliptic Tales: Curves, Counting & Number Theory (Princeton University Press)
• B. ARTMANN, Euclid, The Creation of Mathematics (Springer)
• Dave BENSON, Music: a Mathematical Offering (version en ligne, 2008)
  
• L. BERGGREN, J. BORWEIN, P. BORWEIN, Pi, a Source Book (Springer)
• H. BOAULEM, R. BROUZET, La Planète R (Dunod)
• C. BREZINSKI, History of Continued Fractions and Padé Approximants (Springer)
• F.CONTI, E. GIUSTI, Au delà du Compas: la Géométrie des Courbes (Diagonale)
• R. DUNLAP, The Golden Ratio and Fibonacci Numbers (World Scientific)
• J. GRAY, A History of Abstract Algebra (Springer)
• E. HAIRER, G. WANNER, Analusis by its History (Springer)
• R. HERZ-FISCHLER, A Mathematical History of the Golden Number (Dover)
• P. HEYMARD, J.-P. LAFON, Autour du  Nombre Pi (Hermann)
• X. HASCHER, A. PAPADOPOULOS, Leonhad Euler: Mathématicien, Physicien & Théoricien de la Mudique (CNRS Éditions)
• J. HAVIL, The  IrratiΦnals (Princeton University Press)
• J. HAVIL, Gamma  (Princeton University Press)
• W.R. KNORR, The Ancient Tradition of Geometric Problems (Dover)
• N. MAHAMMED, Sur la Résolution des Équations Algébriques (Diderot)
• E. MAOR, The Pythagorean Theorem (Princeton University Press)
• P. NAHIN, An Imaginery Tale: the Story of i (Princeton University Press)
• P. NAHIN, Dr Euler's Fabulous Formula (Princeton University Press)
• I. NIVEN, Irrational Numbers (Wiley)
• I. NIVEN, Numbers: Rational & Irrational  (The L. W Singer Company)
• C. OLDS, Continued Fractions (MAA)
• A. OSTERMANN, G. WANNER, Geometry by its History (Springer)
• P. PESIC, Abel's Proof  (MIT Press)
• P. RIBENBOÏM, My Numbers, my Friends: Popular Lectures on Number Theory (Springer)
• M.SERFATI, Quadrature du Cercle, Fractions Continues et Autres Contes (Brochure APMEP n°85)
• J. STILLWELL, Mathematics and its History (Springer)
• W. STEIN, Elementary Number Theory : Primes, Concgruences & Secrets (Springer)
• G. TOTH, Glimpses of Algebra and Geometry (Springer)
• S. VAJDA, Fibonacci & Lucas, and the Golden Section (Hellis Horwood)

Ouvrages de Références (niveau ***, Profs)

• D. DUVERNEY, Théorie des Nombres (Dunod)
• F. GOMES-TEIXEIRA, Traité des Courbes Spéciales et Remarquables (J. Gabay)
• G. HARDY, E. WRIGHT, An Introduction to the Theory of  Numbers (Oxford)
• A. KNAPP, Elliptic Curves (Princeton University Press)
• W. LEVEQUE, Foundamentals of  Number Theory  (Dover)
• J.H. SILVERMAN, J.TATE, Rational Points on Elliptic Curves (Springer)
• J.H. SILVERMAN, A Friendly Introduction to Number Theory (Pearson)
• M.WALDSCHMIDT, Nombres Transcendants. (Springer, Lecture Notes in Mathematics 402).

Articles (Profs)

• R. TENANT, Medieval Islamic Architecture, Quasicrystals, and Penrose and Girih Tiles
• M.WALDSCHMIDT, Les Débuts de la Théorie des Nombres Transcendants. (Cahiers d'Histoire des  Mathematiques de l'Université Pierre et Marie Curie, n°4).

Sur la Toile

•  Site du Giardino de Archimede: Exposition Oltre il Compasso 
•  Site du Musée de Modène: Exposition Theatrum Mechanicum, Strumenti per la Geometria
• La Géométrie de Descartes, par Patrice DEBART
• La Duplication du Cube, Site de l'IUFM de la Réunion
• Alain Juhel: Irrationalité et Transcendance: État des Lieux avant Hermite , conférence aux journées Padé (Lycée Faidherbe, Lille, 1994).
• Site de Michel Waldschmidt
• Site du Mathouriste

Revenir à la Home Page du Mathouriste