Le Darb-e-Imam à Isfahan:
plus de cinq siècles d'avance sur un prix Nobel ?
"Ispahan
a des tons bleus, si puissants et si rares que l’on songe
à des pierres fines, à des palais en saphir,
à d’irréalisables splendeurs de
féeries…"
Pierre Loti, Vers Ispahan ( 1904)
Pierre Loti, Vers Ispahan ( 1904)
"Isfahan est la moitié du monde..." dit-on depuis bien longtemps en Perse. Les splendeurs des époques Seljoukide (XI-ème siècle) et Séfévide (XVII-ème siècle) qui sautent aux yeux du visiteur ne doivent pourtant pas faire oublier qu'elle renferme bien d'autres trésors. C'est un monument un peu moins fréquenté que le Mathouriste vous invite à découvrir ici; c'est aussi l'histoire d'une belle rencontre à travers les siècles, celle d'un artiste Persan anonyme et d'un chercheur Israélien, lauréat du Prix Nobel de Chimie 2011. Et, que le lecteur se rassure: les mathématiques, loin d'être absentes, en seront le ciment intemporel!
Le Monument
Situé un peu à l'Ouest de la célèbre Mosquée du Vendredi, dans le quartier de Dardasht, le Darb-e-Imam est un complexe funéraire bâti sur un ancien cimetière du X-ème siècle, dont la partie essentielle est un Imamzadeh, ou mausolée pour deux descendants du quatrième calife et gendre de Mahomet, Ali, personnage clef de l'Islam Chi'ite. Commencé en 1453, il s'est vu adjoindre à l'époque Séfévide les deux coupoles (1601pour la plus grande, 1670 pour la plus petite) dont la proximité inusuelle est la caractéristique première qui s'impose au regard.Entrée de la cour, face à l'Imamzadeh
Sitôt
franchie l'entrée, on pénètre dans une
vaste cour...
| Darb-e-Imam, la cour | |
et l'attention des
visiteurs (a fortiori des photographes) est immédiatement
captée par le pishtak
(portail d'entrée du mausolée),
élément typique de l'architecture seldjoukide en
Asie Centrale.
Mais, quelle qu'en soit la finesse... est-ce l'élément le plus original du monument?
Non, et, hasard probable... il suffit de suivre la direction indiquée par le regard du lion de pierre!
Mais, quelle qu'en soit la finesse... est-ce l'élément le plus original du monument?
Non, et, hasard probable... il suffit de suivre la direction indiquée par le regard du lion de pierre!
| Protecteur du peuple, bien
à l'abri dans sa gueule... Mais malheur à lui s'il désobéit! |
Les deux panneaux au
dessus des arcs (fléchés en rouge), de part et
d'autre du pishtak,
sont identiques et ornés d'un fort classique pavage
périodique, obtenu par répétition d'un
motif
hexagonal. La surprise vient du panneau en léger
renfoncement,
à gauche (flèche verte) qui n'a curieusement pas
son
pendant dans la partie droite. Toute symétrie n'en est pas
absente: il possède un axe vertical évident; mais
en
revanche, aucune
répétition périodique n'y
apparaît clairement.
Et alors? Qu'est-ce qui prouve que ce panneau n'est pas qu'une petite parcelle d'un motif plus vaste, "débordant", en quelque sorte, de ce cadre et qu'on pourrait, lui répéter périodiquement?
L'objection est tout à fait sérieuse à ce stade, et certains chercheurs n'ont pas manqué de la faire, avançant même des propositions de complétion en un motif que l'on pourrait ensuite répéter périodiquement à l'infini. Pourtant, on verra que, sous une hypothèse de conception, à la fois solide archéologiquement et raisonnable mathématiquement, nous sommes bien là en présence d'un pavage non périodique du plan, avec cinq siècles d'avance sur leur découverte mathématique... et dix ans de plus avant que cette recherche "gratuite" ne trouve son reflet à l'intérieur de la matière!
Et alors? Qu'est-ce qui prouve que ce panneau n'est pas qu'une petite parcelle d'un motif plus vaste, "débordant", en quelque sorte, de ce cadre et qu'on pourrait, lui répéter périodiquement?
L'objection est tout à fait sérieuse à ce stade, et certains chercheurs n'ont pas manqué de la faire, avançant même des propositions de complétion en un motif que l'on pourrait ensuite répéter périodiquement à l'infini. Pourtant, on verra que, sous une hypothèse de conception, à la fois solide archéologiquement et raisonnable mathématiquement, nous sommes bien là en présence d'un pavage non périodique du plan, avec cinq siècles d'avance sur leur découverte mathématique... et dix ans de plus avant que cette recherche "gratuite" ne trouve son reflet à l'intérieur de la matière!
| Darb-e-Imam, le fronton | |
Des Pavages Périodiques aux Quasi-cristaux
Quelques préliminaires sont indispensables avant de nous lancer dans l'analyse de ce fronton.Pavages et Décoration: l'Art et la Manière
Dans l'architecture islamique, la première évidence que l'on perçoit de la plupart des décorations des monuments est la périodicité: un motif se répète, égal à lui même, dans deux directions du plan. Les façons dont un plan (supposé infini!) est ainsi pavé ne sont pas toutes les mêmes, et le Darb'-e-Imam lui même nous en fournit des exemples: en 1, la "maille" (cellule de base) est hexagonale, elle est carrée dans 2 ou 3. Le pavage 1 entier est invariant par des rotations successives de 60° autour d'un sommet, alors qu'en 2 ou 3, ce n'est manifestement pas le cas; au contraire, des rotations de 90° autour des sommets les conservent; il n'en irait pas de même pour 1. Plus subtile est la différence entre 3 et 5: en 5, il y a bien invariance par des rotations de 90°, mais elles ne sont pas centrées sur un axe de symétrie de la figure.Par contre, 2, 3 et 4 varient en taille, en dessin, en matériau, mais pasdans la manière dont les motifs s'agencent les uns par rapport aux autres. Le mathématicien les met donc "dans un même sac" du point de vue de l'orgagnisation interne du pavage. Pour mieux appréhender l'extraordinaire variété de motifs possibles, voir les célèbres gravures de M.C.Escher. (exemple de galerie de pavages d'Escher, par le mathématicien/informaticien Jos Leys)
Les "manières de paver" le plan sont donc classifiées selon les transformations géométriques laissant la figure invariante; pour chacun des cas 1,3,5 ce sont des groupes de transformation différents. Le mot peut être pris dans un premier temps en son sens le plus vague; il peut -et doit, pour avancer l'étude précise- être pris dans son acception mathématique (voir une présentation élémentaire dans un contexte artistique et architectural).
| Pavages différents, pavages similaires | Une cellule de base carrée se répète... |
On a
démontré qu'il n'y a que 17 manières
différentes de paver un plan au sens que l'on vient de
donner.
Une légende court chez les mathématiciens: elles
sont
toutes présentes dans un seul monument, l'Alhambra de
Grenade. Mais s'ils sont nombreux à le dire... la
plupart ont
répété sans contrôler ce que
d'autres
avaient dit avant eux! À leur décharge, une
vérification personnelle prendrait plusieurs jours aux plus
sagaces, et quelques batailles par articles interposés se
sont
déroulées depuis 1984. Pour Marcel Berger, qui
fait
autorité en matière de
Géométrie (tout en
reconnaissant s'être lui aussi fait pièger
à
recopier cette affirmation dans ses ouvrages des années 1970)
13
sont sûres, 16 envisageables ... et le 17ème
à
Tolède, si vraiment l'honneur de l'Espagne est en jeu (voir
son
livre Géométrie
Vivante,
p.697). Pour intéressant et riche que soit ce
débat, nous
n'en dirons pas plus, sous peine de trop nous
éloigner.

Grenade (Espagne): l'Alhambra et au fond, la bien nommée Sierra Nevada
Et lorsqu'on quitte le plan pour l'espace, ce nombre monte à 230 (!)
De plus, dans les exemples observés, les invariances par rotation se limitaient à des rotations de 90° (qu'on qualifie "d'ordre 4", parce qu'il en faut 4 successives pour revenir à l'identité) ou multiples, 60° (ordre 6, de façon similaire) ou multiples. Ce n'est pas fortuit: on démontre que seuls les ordres 1, 2, 3, 4 et 6 sont possibles, c'est le théorème de restriction cristallographique (démonstraion dans la page liée, pour les amateurs). En particulier, chose très importante pour la suite, les rotations d'ordre 5 se trouvent bannies!
Grenade (Espagne): l'Alhambra et au fond, la bien nommée Sierra Nevada
Et lorsqu'on quitte le plan pour l'espace, ce nombre monte à 230 (!)
De plus, dans les exemples observés, les invariances par rotation se limitaient à des rotations de 90° (qu'on qualifie "d'ordre 4", parce qu'il en faut 4 successives pour revenir à l'identité) ou multiples, 60° (ordre 6, de façon similaire) ou multiples. Ce n'est pas fortuit: on démontre que seuls les ordres 1, 2, 3, 4 et 6 sont possibles, c'est le théorème de restriction cristallographique (démonstraion dans la page liée, pour les amateurs). En particulier, chose très importante pour la suite, les rotations d'ordre 5 se trouvent bannies!
Le Système des Gereh
Comment les carreleurs procédaient-ils? Une possibilité est évidemment de réaliser in situ les constructions géométriques nécessaires. Mais un autre système a été découvert et remis à l'honneur, notamment par Peter Lu, celui des Gereh. Le mot signifie "tuile" en Persan, de sorte que mieux vaut éviter le pléonasme Girih Tiles! Il s'agit de polygones sous-jacents aux dessins, les tuiles portant chacune des segments se raccordant de façon parfaitement rectiligne lors de l'assemblage des pavés. Le système complet comporte 5 tuiles, avec des angles bien précis (pour pouvoir se raccorder sans laisser le moindre interstice), mais on peut n'en utiliser qu'une partie, comme on le verra dans le cas qui nous intéresse.| Les 5 tuiles de base (Wikipedia Commons) | Exemple de pavage (Wikipedia Commons) |
Les couleurs ne sont
utilisées
ici que pour mieux visuliser l'assemblage; dans un travail effectif les
bords des pavés ne seront pas visibles (à la
façon
de traits de construction réalisés au crayon, et
gommés d'un dessin à l'encre
définitif); au
contraire les lignes bleues seront soulignées, et des
figures
complémentaires dessinées et colorées.
Ce système est attesté archéologiquement par un rouleau du XVème siècle conservé au musée de Topkapi, à Istanbul (Turquie); il comporte 114 exemples de schémas.
La méthode semble avoir été utilisée, de manière alternative à un tracé direct, dès 1200, pour produire des décors périodiques. Peter Lu cite l'exemple d'une tour funéraire (géométriquement très intéressante par ailleurs!), en Azerbaïdjan Iranien.
Ce système est attesté archéologiquement par un rouleau du XVème siècle conservé au musée de Topkapi, à Istanbul (Turquie); il comporte 114 exemples de schémas.
 |
|
| Rouleau de Topkapi (Univ. Bilkent, Turquie) | Extrait, avec mise en évidence des tuiles (P. Lu, [3]) |
La méthode semble avoir été utilisée, de manière alternative à un tracé direct, dès 1200, pour produire des décors périodiques. Peter Lu cite l'exemple d'une tour funéraire (géométriquement très intéressante par ailleurs!), en Azerbaïdjan Iranien.
Maragheh (Iran), Gumbad-e-Qabud (XII-ème
siècle)...
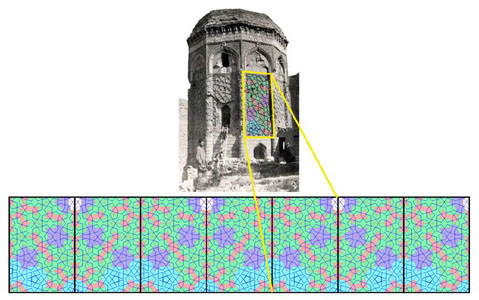
et une "reconstruction" en pavage Gereh, proposée par P. Lu dans [1], [2]
et une "reconstruction" en pavage Gereh, proposée par P. Lu dans [1], [2]
Mais le procédé recèle une puissance supplémentaire, qui va permettre la création de pavages apériodiques et que l'on va voir à l'œuvre au Darb-e-Imam.
Avant les Quasi... les Cristaux!
Il y a deux façons de répondre à une question qui n'est saugrenue que pour celui qui n'a jamais eu le mondre cours de chimie (ou, pire, à qui il n'en est vraiment rien resté!):"Quelle
différence y-a-t-il entre le charbon et le diamant?"
Réponse 1 : Aucune,
ils sont tous deux faits d'atomes de carbone empilés.
Réponse 2 : elle est énorme: leurs systèmes cristallins sont différents, et les propriétés physiques et chimiques qui résultent de cette organisation reflètent, en l'amplifiant au niveau macroscopique, cette différence d'organisation des atomes. Alors que le graphite a un réseau formé de mailles hexagonales dans des plans parallèles, sans liason entre eux, le diamant s'organise suivant un système dérivé du système cubique à face centrée, chaque atome y étant fortement lié à ses voisins.

Diamant (à gauche) et graphite (à droite). Source: article "Diamond" de Wikipedia.
Examiner ces différences n'est pas notre propos (pour les curieux, voir ici ou là ). Il est seulement de comprendre que le chimiste fait avec les atomes ce que le maçon-décorateur fait avec les briques, et que l'essentiel est la façon d'organiser. Sans surprise, elle utilise aujourd'hui la théorie des groupes dans un domaine comme dans l'autre; ce sont les mêmes mathématiques appliquées à deux domaines qui partagent un même modèle.
Réponse 2 : elle est énorme: leurs systèmes cristallins sont différents, et les propriétés physiques et chimiques qui résultent de cette organisation reflètent, en l'amplifiant au niveau macroscopique, cette différence d'organisation des atomes. Alors que le graphite a un réseau formé de mailles hexagonales dans des plans parallèles, sans liason entre eux, le diamant s'organise suivant un système dérivé du système cubique à face centrée, chaque atome y étant fortement lié à ses voisins.

Diamant (à gauche) et graphite (à droite). Source: article "Diamond" de Wikipedia.
Examiner ces différences n'est pas notre propos (pour les curieux, voir ici ou là ). Il est seulement de comprendre que le chimiste fait avec les atomes ce que le maçon-décorateur fait avec les briques, et que l'essentiel est la façon d'organiser. Sans surprise, elle utilise aujourd'hui la théorie des groupes dans un domaine comme dans l'autre; ce sont les mêmes mathématiques appliquées à deux domaines qui partagent un même modèle.
Petite Chronologie
- 632-732 : en un siècle, la fulgurante conquête Arabe impose l'Islam dans un vaste Empire qui s'étent de l'Espagne et du Maghreb jusqu'aux confins de l'Asie Centrale.
- 800 - 1700 (environ) : L'interdiction de représenter la figure d'Allah ou du Prophète stimule l'imagination géométrique des artisans qui décorent mosquées, tombeaux et Madrassas; au fil des ans, ils s'enhardissent à des constructions de plus en plus complexes.
- 1200 (environ): Apparition (Maragheh, Gumbad-e-Qabud) de la méthode de construction des motifs décoratifs par le système des Gereh.
- 1333-1354 : construction de l'Alhambra de Grenade. Il est réputé présenter, dans ses décors, les 17 seuls types de pavage périodique possibles. Toutes les possibilités sont épuisées, mais on ne dispose alors d'aucune preuve du fait qu'il n'en existe pas d'autre ("J'ai tout essayé et je ne n'y arrive pas" n'est pas un argument mathématique, car un doute subsiste toujours: et s'il y en avait un 18-ème, très subtil, bien caché, que seuls une intelligence supérieure et un travail acharné découvriraient plus tard?)
- entre 1500 et 1600 : le rouleau de Topkapi recense systématiquement des procédés de construction par le système des Gereh.
- 1784
: Haüy écrit son
premier ouvrage sur la cristallographie; un traité complet suivra
en 1822.
| Ouvrage en ligne sur le site Gallica de la BnF | |
- 1832 : naissance de la théorie des groupes (à propos des équations algébriques) et mort en duel de son fondateur, Évariste Galois.
- 1849 : Auguste Bravais,ex-Polytechnicien, recense, grâce à l'emploi de méthodes géométriques les 14 systèmes cristallins de l'espace; on les nommera en son honneur réseaux de Bravais.
- 1872 : Felix Klein publie le Programme d'Erlangen, texte aride, mais qui révolutionne la vision de la Géométrie, désormais structurée par la théorie des groupes.
- 1912
: Max Von Laue apporte la
confirmation expérimentale de l'hypothèse de
Bravais, en employant la technique de diffraction des rayons X,
qu'il vient de mettre au point: elle lui vaudra le prix Nobel de
Physique 1914). Elle va devenir la méthode courante
d'étude des structures cristallographiques; le point important,
pour la suite, est le suivant: les figures de diffraction ne sont pas
des photographies exactes du cristal, de la disposition des atomes,
mais elle doivent observer les mêmes symétries que celui-ci. Les rotations d'ordre 5 (ou 10) doivent donc en être bannies.
Bravais (Wikipedia Commons)
Von Laue (Wik. Commons) - 1936
: Heinz
Voderberg réalise le premier pavage en spirale, à
l'aide
d'une seule tuile à 9 côtés. Il est en
particulier
apériodique, mais...
deux de ses tuiles mise tête-bêche forment un
octogone qui
pave le plan de manière périodique! Les
mathématiciens conjecturent, de plus en plus fortement, que
tout
système fini de tuiles pavant le paln de façon
apériodique peut être, comme dans cet exemple,
réagencé en un pavage
périodique.

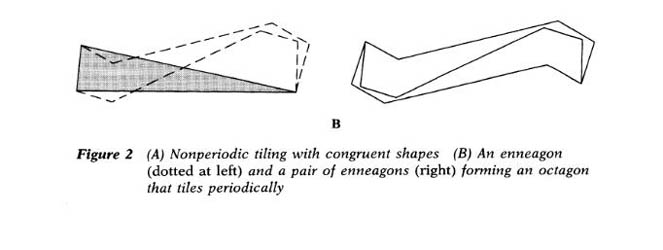
figures extraites de Martin Gardner, Penrose Tilings
- 1974
: Roger Penrose
exhibe un premier ensemble de six tuiles (dont 3 pentagones et une
étoile à cinq branches) qui infirme la
conjecture: il
pave le plan, mais seulement de manière
apériodique.
Puis, il construit un deuxième ensemble plus simple:
seulement
de deux tuiles (la
flèche et le cerf-volant). Avec,
de plus, une structure
hiérarchique: chaque cerf-volant se
découpe en deux cerfs-volants et deux demi
flèches; chaque flèche se découpe en
un cerf-volant et deux demi-flèches, semblables
(mêmes angles) à 'un facteur d'aggrandissement
près (voir l'article
Wikipedia Penrose Tiling)
. C'est drôlement beau, mais ça ne sert
à rien...
les mathématiciens sont décidément des
rêveurs incorrigibles.
Penrose sur un sol représentant son premier pavage (Université A&M du Texas, Austin)
Images provenant de l'article Wikipedia Penrose Tiling
- 1982 : Daniel Schechtman (Université Technion, Haïfa, Israël) découvre, en analysant un échantillon d'alliage Zinc-Manganèse-Holmium, des figures de diffraction présentant de nombreuses symétries pentagonales ou décagonales: elles violent donc le théorème de restriction cristallographique! Il se résout à publier après deux ans de vérifications, mais essuie immédiatement l'hostilité de nombreux collègues, dont, pour les dix ans qui suivent, celles du double prix Nobel Linus Pauling, qui va jusqu'à déclarer: "Il n'y a pas de quasi-cristaux, il n'y a que des quasi-scientifiques!". Sans se décourager, Shechtman renouvelle les expériences, et les faits têtus, donnent raison à son obstination. Plusieurs centaines de quasi-cristaux sont synthétisés par alliage. Quasi faute d'avoir une structure périodique, mais quasi-cristaux parce qu'ils partagent avec ceux-ci un spectre de diffraction discret. Et pour qui un outil de description mathématique est déjà là: les pavages de Penrose!
- 2007 : Peter Lu attire l'attention sur les pavages faits selon le système des Gereh et établit, sur le cas du Darb-e-Imam, l'anticipation des quasi-cristaux.
- 2009 : première découverte d'un quasi-cristal à l'état naturel:
- 2011
: Daniel Schechtman voit ses travaux enfin
couronnés par le Prix Nobel de Chimie.
"For
three millennia we have known that five-fold symmetry is incompatible
with periodicity, and for almost three centuries we believed that
periodicity was a prerequisite for crystallinity. The electron
diffraction pattern obtained by Dan Shechtman on April 8, 1982 shows
that at least one of these statements is flawed, and it has led to a
revision our view of the concepts of symmetry and crystallinity alike.
The objects he discovered are aperiodic, ordered structures that allow
exotic symmetries and that today are known as quasicrystals. Having the
courage to believe in his observations and in himself, Dan Shechtman
has changed our view of what order is and has reminded us of the
importance of balance between preservation and renewal, even for the
most well established paradigms."
Sven Lidin, membre du
comité Nobel (début du discours de remise du prix)
Le communiqué de presse du
jury mentionne même le Darb-e-Imam!
Également sur le site Nobel: la présentation grand public, le dossier scientifique de présentation (plus détaillé, mais d'un niveau plus élevé)
Également sur le site Nobel: la présentation grand public, le dossier scientifique de présentation (plus détaillé, mais d'un niveau plus élevé)

