De Pythagore aux Ondelettistes ...
... la Quête de Parseval!
|
"Il
est un petit peu paradoxal de commencer une leçon de 'Mathématiques
d'aujourd'hui' par le théorème de Pythagore. L'idée du théorème de Pythagore
m'est venue pour illustrer les problèmes de vulgarisation mathématique.
On peut, à partir de ce théorème, faire de nombreux développements. Je
vais vous présenter certains dentre eux, en théorie des ensembles, en
analyse multifractale et sur le mouvement brownien. Mais comme j'espère vous en convaincre, on
pourrait aller dans bien d'autres directions, c'est un sujet
efflorescent."
J.-P. KAHANE. Le Théorème de Pythagore, l'Analyse
Multifractale et le Mouvement Brownien (1993)
in Repères IREM n° 27 |
Et pour illustrer la pertinence de ce point de vue, nous allons en explorer l'héritage dans une tout autre direction, celle de l'analyse de Fourier, si chère au conférencier cité. Mais en prenant le temps de nous promener, bien sûr!
Pythagore
Il est partout!
Et d'abord, là où on ne l'attend pas forcément: au portail royal de la cathédrale de Chartres. Les mathématiciens sont plutôt rares dans ce genre d'endroits, où l'on croise plus volontiers anges ou démons -à moins qu'ils ne tiennent des deux... Hommage des compagnons tailleurs de pierres? Ou n'est-ce pas plutôt le rappel du fait qu'on y enseignait encore au XIIème siècle, selon la tradtition antique tardive, les 7 arts libéraux? À lui tout seul, en effet, Pythagore incarne toutes les matières du quadrivium: arithmétique, musique, astronomie et géométrie.| portail de la cathédrale de Chartres: | au dessus de la porte de droite |
Pythagore est à gauche, avec un instrument de musique à corses sur les genoux |
Mais on trouve aussi son image, ou celle de son théorème (par exemple, la figure par laquelle Euclide le démontre), en Italie, en Turquie...
| Musée du Capitole (Rome) |
Musée La Specola, Florence; "Tribune de Galilée" |
Musée d'Aphrodisias (Turquie) |
Samos
Le Mathouriste a projeté, depuis quelque temps déjà, d'y faire une visite, d'autant que Pythagore n'est pas le seul scientifique à être natif de l'île... en attendant, il emprunte ces deux images à un site invitant à venir y passer des vacances. |
 |  |
| Statue et buste à Samos, sa terre natale | Samos, sur un timbre grec |
|
| images provenant du site commercial
(tourisme):
http://www.greece.com/ | ce timbre, et tous ceux montrés danns cette page, à voir sur le site de Jeff Miller | |
|
"J'aimerais
bien vous donner les dates de sa naissance et de sa mort, mais personne
ne les connaît. Pythagore était contemporain de Bouddha [-556,-480] et
de Confucius [-5565,-479],
dont on connaît beaucoup de choses, mais l'Inde et la Chine étaient à
l'époque des nations anciennes et civilissées, contrairement à cette
poussière d'îles de la Grèce ancienne ."
J.-P. KAHANE. Le Théorème de Pythagore, l'Analyse
Multifractale et le Mouvement Brownien (1993)
|
Si la date de décès avancée est exacte, il meurt au moment où va naître Périclès, qui a laissé son nom à cet exceptionnel Vème siècle, celui du "miracle grec". Des mathématiciens grecs que nous connaissons, seuls Anaximandre et Thalès sont plus anciens.
Dans sa légende, on trouve beaucoup de voyages, comme autant d'initiations: en Grèce continentale, en Égypte, en Mésopotamie, en Perse, en Crète...
|
"En
fait, on ne sait rien de précis à son sujet. On ne sait même pas s'il
pratiquait la géométrie, et tous les ouvrages quon lui attribue sont
apocryphes. Il est cependant considéré comme l'inventeur de la
mathématique grecque. Mais ceci est une légende attestée dès le IV ème siécle pour expliquer les origines. Dans le même ordre d'idées, le supposé voyage de Pythagore en Égypte reconstruit pour les anciens un ordre rêvé, une origine de la mathématique, une histoire des temps très reculés. ."
M. NEVEUX, Le Nombre d'Or, Radiographie d'un Mythe (Seuil, 1995)
|
Crotone
On sait en revanche de façon sûre que, banni de Samos par le tyran Polycrate, 'il s'installae à Crotone, en Calabre (au pied de la botte italienne, dans la Grande Grèce d'alors) en 535 av JC. Il y fonde 3 ans plus tard une école, à moins qu'on ne préfère dire une confrérie, voire une secte. Elle est en tout cas nettement hiérarchisée, avecson initiation, ses degrés, dont le plus haut est celui de mathématicien, (celui quii démontre), alors qu'au précédent, celui des acousmaticiens, on se contente d'écouter (comme le suggère l'étymologie) et d'apprendre par cœur les parole du maître . Au menu, philosophie, arithmétique, géométrie, musique, astronomie et... végétarisme!De quoi redevenir bien plus sûrement à la mode qu'avec la géométrie...
La ville lui a rendu hommage avec uun monument en plusieurs pièces, pour évoquer les multiples aspects de son enseignement et de ses recherches.Il a été créé en 1991 par Ludovico Graziani. Bizarrement, le théoème n'y est guère en vedette; on aperçoit une équerre au bas de la plaque, et à côté des solides géométriques. L'autre personnage, à gauche, est Alcméon de Crotone, médecin, astronome, et bien sûr philosophe pythagoricien.
 |
 |
 |
Le disque vertical évoque les deux grand sévènements quo'nt été la fondation de la ville et la création de l'école pythagoricienne.
 |

|

|
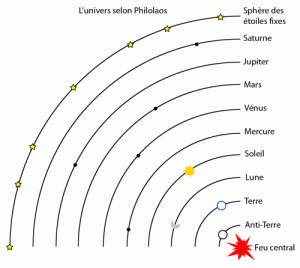 |
Une autre partie évoque la cosmographie de Pythagore; son piédestal est formé de deux pentagones, reposant eux-mêmes sur une étoile à 5 branches, autres éléments forts de la symbolqiue pythagoricienne. Ce système, avec 10 sphères emboîtées. est attribué à un disciple du maître, Philolaos de Crotone. La Terre n'est pas immobile au centre du monde, elle tourne... mais autour d'un "feu central", comme le soleil, la lune (qui ne font que réfléchir la lumière de clui-ci) et une curieuse anti-terre! Sert-elle à obtenir un beau nombre 10 = 2x5 de sphères? à nous cacher le feu central? Mystère! |
|
source du schéma explicatif: cette page de l'Observatoire de Paris; vous y trouverez plus de précisions.
|
On peut aussi retrouver dans la ville, au hasard des rues, le nom de son citoyen le plus célèbre... chacun appréciera la mise en valeur!
 |
|
"À
peine arrivé au port nonchalent de Crotone, il discerne devant les
maisons des femmmes aux cheveux torsadés en train de se barbouiller le
visage de blanc de céruse, mêmant à ce résidu de plomb une poudre de
racines, ce qui leur rosit les joues comme les Athéniennes. Lui, rêve
d'une femme fière dans son vêtement plissé sous les seins, brune de
peau, grimpant les côtes odorantes dans des bottines élégantes ou des
sandales serées aux chevilles; elle saurait lire et conter l'Illiade et
l'Odyssée à leurs enfants. Il a assez voyagé et pensé sa vie: il veut
une épouse véritable, instruite, belle, paisible. Les femmes qui ne
vibrent pas au ciel, à la lyre et aux poèmes d'Homère le lassent. [...]
Soudain, une femme élancée vient au devant de lui, c'est une prêtresse, qui le salue, et ose le regarder comme une lionne son petit. [...] - Ton teint est clair et sans céruse... Je n'ai jamais vu femme telle que toi. Je ne t'ai pas même rêvé et pourtant.... -Je ne nage quau soleil levant ou couchant, ainsi je n'ai pas à me peindre en blanc! Si tu veux me revoir, j'appartiens à ce temple que tu aperçois entre les cyprès. Je me nomme Théano. [...] |
Raphaël, Lécole d'Athènes, détail (copie à la Bibliothèque Sainte Geneviève, Paris)
Pythagore est le personnage qui écrit dans le livre; à côté de lui, Théa tient l'ardoise |
|
Lorsqu'il
veut contempler le visage de la prêtresse, elle a déjà emprunté un
chemin de chèvres. Cette femme s'affirme en marchant gallairdement, son
corps fait penser à un ruisseau en plein désert. Elle semble
impassible, mais elle ondule comme la foudre. Pythagore est touché au
cœur. [...]
Le soir même, il se rend chez un hôte illustre: son ami Brontinos, qui n'est autre que le père de la belle inconnue.Théano rempote des plants de basilic et salue avec ironie l'ami de son père. Pythagore ne la quitte plus des yeux."
H. CHARDAK, L'Énigme Pythagore
|
|
S'il est bien établi que l'école fut florissante et marqua durablement les esprits, on sait, faute d'écrits, bien peu de choses sur ce qui s'y discuta; ceux qui évoquent les pythagoriciens le font à un, voire plusieurs siècles d'écart... peut-on vraiment s'y fier? Un principe unificateur, les nombres régissent toutes choses, entraîne des correspondances parfois plus ésotériques que scientifiques, entre arithmétique, astronomie, géométrie et musique. Exemple de ces attributions incertaines, les 5 solides dits platoniciens: autant on est certain de leur mention (correspondance aux éléments comprise) dans le Timée de Platon, autant on ne peut confirmer par recoupements cette affirmation de Plutarque, reprise quatre siècles plus tard par Diogène Laërce.:
Cela peut sembler naïf, mais Képler lui-même, en 1596, commencera ses travaux en misant sur des correspondances entre ces solides et les planètes connues...
Une preuve de l'importance du groupe est le grand nombre de ses membres On en trouvera des listes partielles ici et là..
Outre Théano (ce n'était pas la seule femme, et sur ce point Pythagore était très en avance), Alcméon et Philolaos déjà cités, ceux qui retiendront particulièrement l'attention des mathématiciens sont Hippase de Métaponte et Archytas de Tarente Au premier s'attache la légende d'avoir été noyé pour avoir révélé l'existence du nombre irrationnel 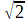 ,
comme diagonale d'un carré de côté 1. Et si Jamblique donne une version
quelque peu différente, il n'échappe pas au châtiment, et le motif en
reste la divulgation d'un secret de la confrérie, en l'occurrence celui
qu'on a présenté juste au dessus! ,
comme diagonale d'un carré de côté 1. Et si Jamblique donne une version
quelque peu différente, il n'échappe pas au châtiment, et le motif en
reste la divulgation d'un secret de la confrérie, en l'occurrence celui
qu'on a présenté juste au dessus!
Archytas l'auteur d'une des premières solutions du problème de Délos (construction, grâce à une courbe auxiliaire, de certains irrationnels inconstructibles à la règle et au compas). Sont également cités comme pythagoriciens d'autres qui prirent une part active à létude de ce problème: Hippocrate de Chios, Dioclès . |
Buste d' Archytas au Musée de Naples |
Mort à Métaponte
Les versions diffèrent; l'auteur ci-dessous en donne lui-même trois. On
y retrouve toujours le refus de piétiner les fèves, sur lesquelles il
avait jeté un intedit alimentaire strict.|
" Voici comment mourut Pythagore. Il séjournait avec ses disciples dans la maison de Milon,
quand cette maison fut incendiée par un homme jaloux de n’avoir pas été choisi comme élève par le
philosophe. On accuse parfois les Crotoniates de ce crime en disant qu’ils
craignaient que Pythagore ne devînt tyran de leur ville. Toujours est-il que
le philosophe prit la fuite et fut rejoint près d’un champ de fèves. Il refusa
de le traverser en déclarant qu’il préférait être tué à fouler les fèves aux
pieds, et en ajoutant qu’il valait mieux mourir que parler.
Ses poursuivants le mirent à mort, et avec lui la plupart de ses compagnons,
au nombre de quarante environ. Quelques-uns purent s’enfuir, entre autres
Archippe de Tarente et Lysis déjà nommé. Dicéarque prétend que Pythagore mourut
dans le temple des Muses de Métaponte où il s’était réfugié, après un jeûne de quarante jours." Diogène Laërce, Pythagore
|
LE fameux Théorème
|
" [...] ce n'est pas moi qui le dis. C'est Pythagore. Et croyez-vous qu'il fût con, Pythagore ?
Évidemment non, sous-doués que vous êtes. S'il avait été con,
Pythagore, je vous le demande, aurait-il inventé le thé au rhum ?
Est-ce qu'il aurait découvert la maladie de Carré, dont souffre notre
estimé confrère Luis Rego ici présent depuis qu'il s'est coincé
l'hypoténuse dans un placard à balais ? "
P. DESPROGES. Les Réquisitoires du Tribunal des
Flagrants Délires (contre
Gisèle Halimi, 1982)
|
C'est l'une des plus célèbres figures de la géométrie, et on la voit ci-contre sur cet insigne maçonnique. Elle vient directement de la figure donnée par Euclide dans ses Éléments (voir ci-dessous); le théorème exprime en effet que "
Dans un triangle rectangle, le carré de l'hypoténuse est égal à la
somme des carrés des deux autres côtés."
La figure met en évidence, sous forme géométrique, les trois carrés qui interviennent, signifiant que l'aire du plus grand est égal à la somme des deux autres aires. On peut d'ailleurs en voir une monstration (entendons par là: ce n'est pas une démonstration, une preuve, mais cela permet de constater le fait sur un exemple) à la Cité des Sciences; elle est reprise dans cette vidéo. |
|
| en exposition à la Grande Loge de France,
Journées du Patrimoine 2010 |
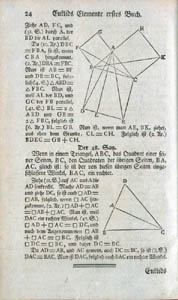
La figure des Éléments, bestseller mathématique après sa redécouverte ( Rome et le christianisme ayant perdu, par leur total désintérêt tout l'héritage scientifique grec, il ne nous est revenu qu'à la fin du moyen-âge, la transmission ayant été assuré par l'empire d'Orient et ses successeurs musulmans) est agrémentée de lignes de construction à fins de démonstration.
 |
 |
 |
|
| en
grec ancien (1825, d'après. Peyrard) |
Luca della Robbia, Euclide et Pythagore. Musée de l'œuvre de la cathédrale de Florence |
en latin, traduit par l'anglais Isaac Barrow (1638) |
en
allemand (1781)
|
Preuves
Mais la manière d'Euclide est loin d'être la plus douce pour aborder la démonstration. Et il y a tant de façons d'opérer...|
" Il y a autant de démonstrations du
théorème attribué à Pythagore que d'églises à Rome. Ce sont des variantes de trois prototypes:
la preuve du puzzle, la preuve d'Euclide, et la preuve de l'homothétie.
La démonstration d'Euclide ne semble pas assez "primitive" pour être pythagoricienne." P. Brémaud. Le Dossier Pyhtagore
|
Suivons cette classification, et commençons par la plus simple, celle avec lesquelles on aurait envie de jouer dès l'école primaire!
Preuves par découpage
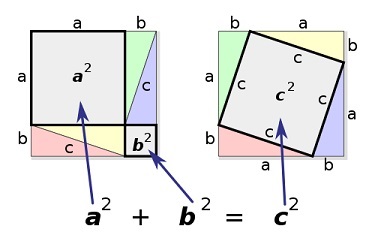
La plus immédiate consiste à comparer deux manières d'évaluer l'aire
d'un carré de côté a+b, a et b étant les deux côtés de l'angle
droit du triangle d'hypothènuse c:( a + b )² = a² + b² + 4. (½ ab ) = c² + 4. (½ ab )
en disposant les quatre triangles rectangles de deux façons
différeentes. Elle est souvent appelée preuve chinoise
, car elle provient du Zhoubi Suanjing, alias Chou Pei Suan Jing
(circa. 1100 av. J.C.) Se peut-il qu'elle ait inspiré une œuvre d'art
révolutionnaire?Peut-être trouvez-vous ce rapprochement saugrenu? Tiré par les cheveux? Ces malades de mathématiciens, ils voient leurs obsessions partout, n'est-ce pas? Ne concluez pas trop vite: la preuve d'Abu-al-Wafa (940-998) a été intentionnellement reproduite dans l'iwan ouest de la Mosquée du Vendredi d'Isfahan! Algébriquement, avec un petit carré central de côté a-b, cela équivaut à:
( a + b )² = ( a - b )² + 8. (½ ab ) = c² + 4. (½ ab )
Preuve d'Euclide
La façon la plus agréable de la
visualiser est la version d'Oliver Byrne (1847), qui a eu l'excellente
idée non seulement de la mettre en couleurs, mais d'en faire suivre la
progression colorée de manière dynamique... et ce, bien avant le temps
des vidéos sur Internet! ... C'est tout le traité d'Euclide,
d'ailleurs, qu'il présente ainsi; voici le résultat: n'est-il pas
plus facile à suivre? |
 |
 |
| page de
titre |
la
démonstration |
couverture |
Profitons en pour revenir sur notre "exagération" précédente, relative à Malevitch: l'endroit est idéal pour vous convaincre que ce n'en était pas une; car l'auteur de cette page a testé sur différents publics, en conférence, la présentation de l'image centrale de Byrne aux côtés de... mais voyez plutôt!
 |
 |
 |
| Malevitch, Suprématisme n°56 (1936) Musée de l'Ermitage, St-Petersbourg (Russie) |
|
Ican Klioune, Suprématisme (1916) Galerie Tetriakov, Moscou (Russie) |
Et ça marche: colorée, la figure d'Euclide passe pour une estimable toile suprématiste. Piège, pensez-vous? Si le Mathouriste l'a tendu à d'autres, c'est pour vérifier qu'il n'était pas la seule victime ce "test de Rorschach artistique": la première fois qu'il a vu cette image, il l'a immédiatement rapprochée des suprématistes. Simple projection d'émotions esthétiques, et excellente occasion de convaincre ceux qui se disent allergiques aux mathématiques que la figure d'un théorème peut bien, à leur corps défendant, leur procurer une émotion esthétique!
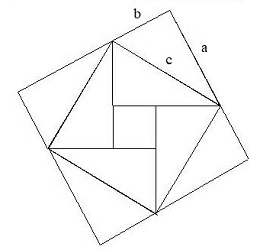
Preuves par similtude
La plus naturelle, car elle ne demande aucune construction auxiliaire.
Mmême l'introduction du carré de côté a+b, dans la preuve chinoise, a un
petit goût d'astuce ingénieuse: il faut penser à introduire une figure extérieure au triangle donné. Ici,
au contraire, on se contente d'abaisser sa troisième hauteur, issue du
sommet droit C; elle
appartient naturellement à la figure du triangle.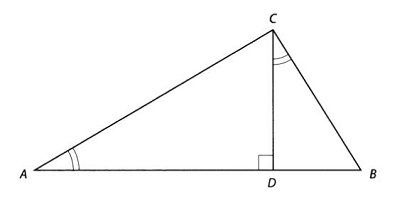 |
Les angles CAD et DCB sont égaux parce que leurs côtés sont perpendiculaires, et donc les triangles CAD et DCB sont semblables. On a donc:
BD / CD = CD
/ AD = BC /
AC
mais aussi, CAD et BAC étant semblables (on a volontairement réécrit le
premier rapport à la fin, pour mieux voir):
AC /
AB = CD / BC
= AD / AC = AC /
AB
d'où enfin donc
BC = BD . AC / CD et
BC = AB . CD /
AC par
produit BC ²= AB . BD
et aussi AC²
= AB . ADAC² + BC ²= AB . AD + AB . BD = AB . (AD + BD) = AB²
Proclus de Lycie (412-485), commentateur d'Euclide, estime que c'est la seule preuve originale que celui-ci ait donné dans les Éléments. C'est aussi la seule fois qu'il donne une deuxième preuve d'un résultat établi bien avant (proposition VI.31, sa preuve classique étant numérotée I.47).
370 + 1 preuves!
La beauté du résultat, son ancienneté ont naturellement fasciné les
mathématiciens de toutes les époques... et beaucoup ont voulu mettre
leur petit caillou sur le cairn, comme le mong des chemins de
randonnée, histoire de dire: "moi
aussi, je suis passé par là, et je dépose ma modeste contribution...".
Le mathématicien E. Loomis (1842-1940) en a recensé 371 dans son
livre The Pythagorean
Proposition: Its Demonstration Analyzed and Classified et,
vous vous en doutez bien, il doit y en avoir plus aujourd'hui... Le
site Cut the Knot vous en donne déjà 118 ici, de quoi se rassasier pour une première
dégustation..Pourquoi en mettre une à part dans notre titre? Ce pourrait être celle d'Euclide, bien sûr, mais le Mathouriste a plus original et... plus touristique a vous proposer: il en a photographié l'auteur à... Washington, le voici!
| statue du
président Garfield ( 1831-1881)devant le Capitole, Washington
(U.S.A.) |
||
| Reconnaissons-le:
ce n'est pas tous les jours qu'on rencontre une démonstration signée
par un président des États-Unis! Enfin, futur, puisqu'il l'a
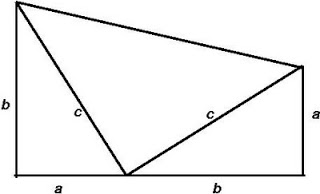
donnée en 1876, 5 ans avant son élection. Elle repose sur la figure suivante, où le triangle est disposé deux fois, mais différemment. On calcule pirectement, ou par somme, l'aire totale de la figure... il suffit de ne pas avoir oublié, depuis le temps de l'école primaire, l'aire du trapèze. |
 |
Des antécédents?
En Mésopotamie?
Quelques tablettes d'argile (essentiellement 4 selon la page historique dédiée de l'univrsité de St-Andrews) suggèrent une connaissance, au moins partielle, du "théorème de Pythagore" en Mésopotamie, 1500 ans avant la naissance du mathématicien de Samos: plus précisément, toutes sont datées dans une fourchette 1900 av. JC, 1600 av. JC, de l'époque d'Hammourabi, dit-on fréquemment, ce qui est une excellente manière de les situer en raccourci par rapport à un autre texte fondateur, gravé, lui, dans la pierre: le premier code juridique connu. Voici les deux plus fréquemment citées:| YBC 7289 ( YaleUniversity, USA) |
Plimpton 322 ( British Museum) | Code d'Hammourabi |
 |
 | |
| cliché Bill Casselman, pour cette page: consultez-la! | portail des IREM, photo C. Proust |
au Louvre (photo personnelle) |
Mais c'est faire un raccourci trop sommaire qu'en déduire ne serait-ce que la maîtrise du résultat "de Pythagore", sans même parler de sa démonstration!
- La première a l'avnatage de comporter une figure, mais ce n'est pas celle du théorème, simplement la présentation du carré et de sa diagonale. Elle n'évoque qu'un seul cas, très particulier -peut-on dire qu'on connaît ce théorème en voyant 1² + 1² = 2? Son but est le calcul numérique de cette diagonale, indiqué avec une très grande précision, sans doute pour servir de facteur multiplicatif pour trouver la diagonale d'un carré quelconque. Elle est un jalon fondateur de l'analyse numérique, quoiqu'on ne connaisse même pas l'algorithme utilisé par le scribe! Ce qui suffit à en faire un objet fascinant, et toujours mystérieux. (voir une analyse détaillée sur le site BibNum ).
- La seconde est plutôt un objet arithmétique: elle donne une liste de triplets pythagoriciens, c'est à dire de nombres entiers vérifiant a² + b² = c². Remarquable, tout aussi fascinant, tout aussi mystérieux quant à son but, encore discuté aujourd'hui (on peut lire un très intéressant article, plutôt récent, qui y voit une table trigonométrique exacte). Pour autant, est-ce qu'une quinzaine d'exemples, que l'on a pu découvrir expérimentalement, sans dessiner la moindre figure, prouve quoi que ce soit sur le versant géométrique du théorème?
En Égypte?
Il
n'est pas faux, de manière
générale, de considérer qu'avec le bénéfice de l'antériorité, la
culture égyptienne a influencé la Grèce naissante. Les bâtisseurs
égyptiens utilisaient la cordes à 13 noeuds,
peu encombrante et si pratique qu'elle sera aussi utilisée sur les
chantiers des cathédrales, notamment Chartres... est-ce la raison qui
vaut à Pythagore de figurer à son portail? Elle permettait aussi bien
de tracer des segments que des angles droits, en joignant ses deux
extrémités pour réaliser le triangle pythagoricien ( 3, 4, 5 ).
Mais, une fois de plus, un exemple ne peut valoir connaissance générale. Invoquer aussi le "papyrus Berlin 6619" n'apporte rien: c'est un problème du second degré où ce même triangle (à un facteur multiplicatif 2 près) n'apparaît qu'au dernier stade, commme solution. |
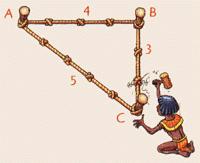 |
| source: Wikipedia, article corde à noeuds |
|
"
Dans 90% des livres, on trouve l'affirmation que les Égyptiens
connaisssaient le triangle rectangle de côtés (3, 4, 5) et qu'ils l'ont
utilisé pour construire des angles droits. Quel crédit accorder à cette
affirmation? Aucun!"
B. Van der Waerden, Science Awakening (Wiley, 1963)
|
Et il ajoute que c'est par recopies successives, les uns sur les autres, qu'ils ont ainsi bâti artificiellement un "fait bien établi", puisque... tous les auteurs le disent! Le procédé a prouvé son efficacité: tous ceux qui remplissent leurs bibliographies en y incluant sans plus de vérifications celles des quelques ouvrages effectivement consultés s'y reconnaîtront; et s'ils se sont crus malins, ils n'ont rien inventé! Sans vouloir les exonérer de leur petit forfait ordinaire, leur confiance pourrait bien venir d'un auteur réputé du premier siècle, qui invoque des raisons plus théologiques que l'inventaire d'une caisse à outils...
|
"
On peut supposer que les Égyptiens
étaient sensibles à la nature de l'univers, et tout particulièrement à
cette beauté suprême des triangles dont Platon semble lui aussi avoir
fait usage dans la République pour représenter le mariage. Ce
triangle a une verticale de 3 unités de longueur, une base de 4, et une
hypothénuse de 5 qui, lorsqu'on l'élève au carré, est égale à la somme
des deux autres carrés. La verticale peut être assimilée à
l'homme, la base à la femme, et l'hypothénuse à leur progéniture; ainsi
respectivement la source Osiris, l'élément réceptif Isis et leur
parfaite réalisation, Horus."
|
Quant aux pyramides...
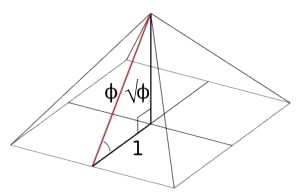
Oui, bien sûr, la hauteur de la pyramide se relie à celle d'une face triangulaire (l'apothème, comme on disait jadis...) par le théorème de Pythagore. Ce n'est pas la preuve qu'il a été utilisé. Un qui y croyait, c'est le très sérieux astronome John Herschel (1792-1871), fils de William, le découvreur d'Uranus. Il écrivit en 1860 un article où il prétendait qu'Hérodote affirmait que les architectes avaient, pour la beauté de leur monument, fait en sorte que l'aire d'une face triangulaire fût égale à celle d'un carré construit sur la hauteur. Former l'équation du second degré qui détermine la hauteur en fonction du côté exige l'emploi du théorème; comble d'esthétique, la solution fournit un "triangle d'or"! Ce que les mesures sur le terrain confirment de façon satisfaisante; et d'ailleurs, elles étaient bien connues à l'époque où Herschel écrivait. D'où un petit soupçon: n'a-t-il pas triché en invoquant Hérodote pour donner plus de poids à ses calculs? Certes, celui-ci mentionne les mesures de la pyramide, mais pour dire que la hauteur est égale au côté! Ce qui est donc grossièrement faux.
 |
 |
|
| source: site "Phi" de Gary Meisner |
||
| William Herschel dans sa maison, à Bath |
Laissons donc la conclusion à un mathématicien (et historien de sa matière) connu:
|
" Il n'y a aucune indication formelle que les
Égyptiens aient eu la moindre notion relative au théorème de Pythagore,
en dépit d'histoires infondées, supposant les angles droits construits
à l'aide d'une corde à 3 + 4 + 5 = =12 nœuds ."
D. Struik, A Concise History of Mathematics (Dover, 1967, en ligne sur Internet Archive)
|
En Chine
Cette fois, on tient du sérieux, avec le Zhoubi Suanjing déjà mentionné. Si on retrouve les triplets en nombres entiers, la différence est dans l'adjonction de la figure géométrique par découpage; ainsi se fait le lien entre arithmétique et géométrie qui manquait tant dans les deux cas précédents; et pour une fois, les spécialistes sont (à peu près) d'accord!| dans une édition d'époque Ming (XVIIème siècle) |
|
Pour l'honneur de l'Europe... Stonehenge?
Il ne manquait plus que cela... voilà qu'on prétend avoir trouvé, dans ce lieu plein de beauté et de mystère -de cela, au moins, on conviendra sans peine!- UN triplet pythagoricien, proportionnel à (5,12,13). Certes, cela change un peu de (3,4,5). Au hasard, quelques échos dans la presse: The Telegraph, The Daily Express, News.com... qui ne manquent surtout pas de vous annoncer la sortie d'un nouveau livre le jour du solstice, évidemment: plus fort que Harry Potter!Pour le charme, quelques images, histoire de vous convaincre qu'on peut apprécier le lieu sans céder à la pseudo-science:
et pour le reste... si vous n'avez pas tiré la leçon de ce qu'on a dit de l'Égypte et de la Mésopotamie, soit votre cas est désespéré, soit vous faites partie d'une secte new-age, ou néo-pythagoricienne au sens philosophico-ésotérique; il n'en manque pas pour aller y célébrer les solstices. Le monument étant daté, pour ses débuts, entre 2800 av JC et 2100 av JC, ce serait idéal pour reprendre le record du théorème, mais quel dommage que ces savants druides ne nous aient pas laissé un manuscrit irréfutable, au moins la figure, s'ils n'avaient pas encore inventé l'écriture... Et puis, est-il bien raisonnable de confier l'honneur de l'Europe à un pays qui s'apprête à la quitter?
Transmission
L'avez vous remarqué? Euclide ne fait aucune attribution à sa célèbre proposition I-47. Mais alors, qui l'a baptisée théorème de Pythagore? Il semble que le premier soit Vitruve (90 av JC-20 av JC), dans son traité d'architrecture, au livre IX; Plutarque lui emboîtera le pas..  |
 |
Il est passablement amusant d'y lire que "Pythagore a inventé l'équerre" (!). Il donne l'inévitable recette (3,4,5), mais souligne en note que la propriété est vraie pour tout triangle rectangle. Encore plus truculente, la note de la page qui contient la figure:
Ces notes sont de l'architecte français Claude Perrault, à qui l'on doit le Louvre, l'Observatoire de Paris... et cette traduction! images et texte complet en ligne sur e|rara |
Vitruve se
contente de donner le résultat, sans la démonstration; concédons lui
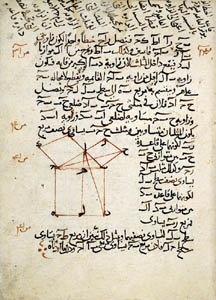
que ce n'est guère la place dans son livre. Quant aux Éléments d'Euclide, ils ont été perdus en Occident, et la faute en incombe doublement à Rome:
Le manuscrit ci-contre est généralement attribué à Thabit ibn Qurra (826-901) |
 |
Géométrie, Arithmétique, ou... Analyse?
À peine posé, le théorème de Pythagore offre d'étonnantes perspectives de prolongement.| Du côté de l'arithmétique, mieux que cueillir des triplets de nombres entiers
à la façon d'un herboriste (ci-contre, le timbre évoque efficacement,
sans le moindre mot ou chiffre le fameux triplet 3,4,5), on peut
vouloir chercher tous les triplets pythagoriciens, i.e:; les triplets d'entiers vérifiant x² + y² = z²
Euclide a donné la paramétrisation des triplets primitifs (premiers entre eux) x = 2uv , y = u² - v² , z = u + v²
Mais ce résultat pousse vers l'étude d'autres exposants que le carré... ce quei nous mène droit à un Himalaya mathématique, le grand théorème de Fermat! |
 |
 |
Du côté de l'analyse... nous rejoignons, comme promis au début de la page, l'analyse de Fourier.
Parseval, nous voilà!
En route vers Parseval...
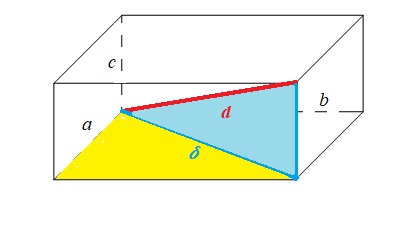 |
Passer de la dimension 2 à la dimension 3, c' est facile. Pour calculer la diagonale du parallélépipède rectangle de côtés a, b, c, et de diagonale d, on applique une première fois le théorème dans le triangle bleu: d² = δ² + c²
mais dans le
triangle jaune:δ² = a² + b²
d'oùd² = a² + b²+ c²
| |
|
 |
Pourquoi ne pas continuer? Il n'est pas plus difficile d'évaluer la longueur d'un vecteur en dimension n; mieux: la figure de dimension 3 va nous aider à "voir" en dimension finie quelconque. Bienvenue dans un monde orthogonal! L'outil pertinent pour ces questions est le produit scalaire des vecteurs, qui permet de dire l'orthogonalité de deux vecteurs et d'évaluer leur longueur. Bienvenue dans le monde riant des produits scalaires ! |
 |
|
| Piet Mondrian, Composition avec bleu, 1926. Philadelphia Museum of Art (USA), | |||
Le tableau qui suit montre que, de l'espace de dimension 3 à un
espace de dimension n
quelconque et à l'espace des polynômes trigonométriques Tn (qui, lui; est de
dimension 2n+1),
tout "fonctionne" de la même manière. Le produit scalaire consiste,
dans chaque cas, à faire la somme des produits deux à deux des
composantes!
Seulement, quand il s'agit de fonctions, la bonne manière est de faire le prosuit des valeurs, et sommer sur l'infinité de valeurs de t grâce à l'intégrale. L'orthogonalité des sinus et cosinus avait été constatée, mais d'un strict point de vue calculatoire, par Fourier pour" légitimer" (mais c'est plus délicat pour une série!) le calcul des coefficients (voir cette page ). Ni lui, ni personne à son époque -et pour presque un siècle encore!- n'avait cette vision géométrique, essentiellement dûe à Hilbert, qui allège les formules e nous " rend la vue", en quelque sorte: nous n'évoluons pas en aveugle dans ces espaces. |
 |
ci-dessus: Piet Mondrian, Composition avec grand plan rouge, jaune, noir, gris et bleu., 1921. Gemeente Museum, La Haye (Pays Bas) ci-contre: Piet Mondrian, Composition en rouge, bleu et jaune 1937-42. MoMA, New York (USA), |
|
| espace |
ℝ3 | ℝn |
Tn = { polynômes trigonométriques
de degré n au plus }
|
| base
orthonormée |
{ i , j , k } | { e1 , e2 , ... , en } | γ0 (t) = 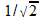 ; γj (t) = cos (jt), 1 ≤ j ≤ n ; γj (t) = cos (jt), 1 ≤ j ≤ nσj (t) = sin (jt), 1 ≤ j ≤ n |
| vecteur |
V = x i
+ y
j + z k |
V = x1 e1 + x2 e2 + ... + xn en | f = (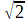 a0 ) γ0
+ a1 γ1 + a2 γ2 + ... + +
an γn a0 ) γ0
+ a1 γ1 + a2 γ2 + ... + +
an γn+ b1 σ1 + b2 σ2 + ... + + bn σn |
| produit scalaire | < V , V' > = V.V' = xx' + yy' + zz' | < V , V' > = x1 x'1 + x2 x'2 + ... +xn x'n | 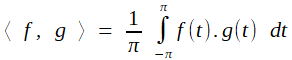 |
| norme
au carré |
|| V ||² = V.V = x² + y² + z² | || V ||² = < V , V > = x1² + x2 ² +... +xn ² | || f ||² = <
f , f > = 2 a0 ²
+ a1² + a2 ² +... +an ² + b1² + b2 ² +... +bn ² |
| orthogonalité | < V , V' > = 0 | < V , V' > = 0 |
< f , g > = 0 |
| coefficients | x = V.i ; y = V.j ; z = V.k | xj = < V , ej > | aj = <
f , γj
> = 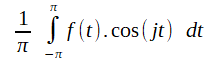 bj = < f , σj > = 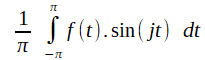 |
Dans l'espace de dimension finie Tn (qui, lui; est ), l'égalité de Parseval est celle que nous avons mise en rouge, ou, pour l'écrire dans sa forme la plus usuelle:
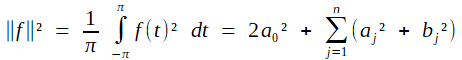
l'énergie du signal est la
somme des énergies de ses composantes de Fourier
C'est remarquable, car à cause de la présence du carré (penser à l'énergie électrique en ri² ), l'énergie n'est pas additive: celle de la somme de deux signaux n'est pas la somme de leurs énergies. Sauf s'ils sont orthogonaux, ce qui est le cas de la base de Fourier.
Mais la grande question est évidemment de savoir si cela s'étend aux signaux "quelconques" (ou presque!), autrement dit au cas des séries. Lorsqu'il y a une infinité de coefficients de Fourier non nuls, a-t-on encore:
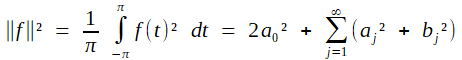 |
Parseval dans le texte
Tous ceux qui ont entendu parler de ce théorème risquent d'avoir un choc: ce texte date de 1799 -il est donc antérieur à ceux de Fourier-, il ne parle pas le moins du monde de séries trigonométriques, et... le résultat est énoncé sans preuve; du moins est-il tenu pour évident (le lecteur est prié de connaître la formule de Moivre...) |
 |
 |
 |
| Dans le
recueil original, les 3 pages du fameux mémoire où figure
l'égalité qui a fait sa gloire (à aggrandir en cliquant) |
|||
En fait, le but est tout autre; Parseval a juste besoin d'un lemme pour sommer une série Aa + Bb + Cc + ... à partir des deux données A, B, C ... et a, b, c ... Il faut sûrement être malin, car le grand Euler a séché, nous précise t-il! Il introduit alors pour la première une série entière génératrice, à la façon d'Euler ou Laplace
A +
Bz + Cz² + ...
mais au lieu de faire de même
pour la deuxième, il la remplace par une série entière en 1/z. Le produit formel
des deux place la somme qu'il cherche comme terme constant
(vérification facile dans le cas de deux suites finies, avec le produit
d'un polynôme en z par un
polynôme en 1/z ). Pour se
débarasser des autres, il a alors l'idée de poser z
= exp(-iu) d'où 1/z =
exp(iu)
intégrer de -π à π fait disparaître tous les termes... peu importe leurs très vilains, très moches coefficients. Seul subsite celui qui nous intéresse! Voilà pour l'évidence, qui en est effectivement une avec deux polynômes, mais pose avec des séries les mêmes problèmes d'interversion que pour le calcul des coefficients chez Fourier... l'époque n'est pas mûre pour cette justification.
C'était le côté face (sombre!), mais pour le côté pile, cela correspond carrément au cas encore plus général
- du calcul du
produit scalaire plutôt que la norme:
<g , f > = 2 a0(f) a0(g) + a1(f) a1(g) +... +an(f) an(g) + b1(f)b1(g) +... +bn(f) bn(g) [+ ... éventuellement]
- de l'utilisation un
produit scalaire hermitien (similaire, mais pour les espaces complexes:
on conjugue tout ce qui concerne g)
Mais qui est Parseval ?
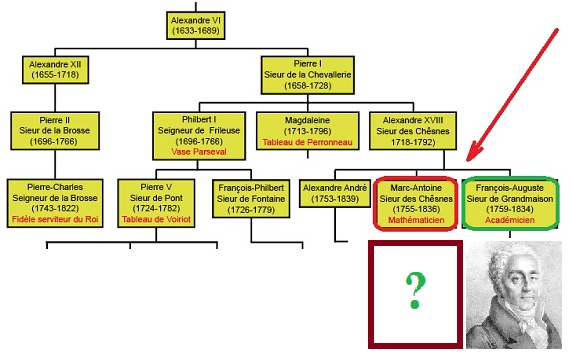
Marc-Antoine Parseval des Chênes (1755-1836) )appartient à l'une des plus anciennes familles de la noblesse française (site web de la famille).
L'extrait ci-contre de l'arbre généalogique (qu'on peut voir au complet) le situe par rapport à ses ancêtres, et à son frère, poète qui accompagna Fourier en Égypte, puis devint membre de l'Institut en 1811. Le mathématicien eut moins de chance: il candidata cinq fois, toujours en vain, à l'Académie des Sciences. Mais il a tout de même une jolie consolation posthume: le voici aujourd'hui certainement plus "immortel" que son frère, et, autre ironie de l'histoire, beaucoup plus compagnon de Fourier, tant ces deux noms sont indissociables dans le plus élémentaire cours sur le sujet. Reste une interrogation:
comment se fait-il que, contrairement à son frère et bien d'autres
membres de la famille, on ne voie nulle part son portrait?
Le Mathouriste
a posé la question à l'aide du contact su site familial, et a obtenu
une réponse très rapide, hélas négative, qui disait en substance: "Nous
serions très intéressés si, de votre côté, vous en dénichiez un, car
c'est le seul dont on n'ait aucune image... Il paraît qu'il était fort
laid, mais est-ce la raison?"
|
 |
||
Faute d'image, nous en avons trouvé deux brèves descriptions qui s'accordent sur la singularité du personnage; la première est dans une sorte de Bottin mondain pour l'année 1836, la seconde est un portrait qu'en dresse un contemporain dans ses mémoires:
| "Le
dernier des trois frères Parseval était une espèce d'ours, fort
original, fort sale et qui s'en piquait, mathématicien du premier ordre
et poète du
dernier rang, qui me confia un jour qu'il avait trouvé un moyen
d'égaler La Fontaine: c'était de faire six cents fables et d'en brûler
cinq cent soixante dix en ne gardant que les trente parfaites. Toute
cette famille avait un petit coup de marteau." |
| Souvenirs du baron de Frénilly, pair de France (1768-1828) |
Sa ville natale,
Rosières-aux-Salines (54), s'est contenté d'un hommage bien
minimal (une ruelle, pas même une rue!), à l'orthographe aussi
incertaine que celle de nombreuses copies d'étudiants... mais, après
tout, le mythe de la table ronde n'est-il pas un avatar du cercle
trigonométrique où naissent toutes les fonctions qui servent de base
orthogonale au développement de Fourier?
Allons donc poursuivre notre balade de ce côté là! |
 |
Prouver la formule de Parseval ?
Il est intéressant d'aller un peu plus loin vers la preuve (la vraie, complète!) du théorème pour deux raisons:- Illustrer la puissance de la vision géométrique en analyse (comment voir un espace de fonction à travers l'image de lespace 3D usuel?);
- voir comment le théorème de Pythagore élémentaire y contribue lui-même (habillé en version produit scalaire et norme, évidemment).
Sn = 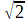 a0 (f) γ0
+ a1 (f) γ1 + a2 (f) γ2 + ... + +
an (f) γn
a0 (f) γ0
+ a1 (f) γ1 + a2 (f) γ2 + ... + +
an (f) γn
+ b1 (f) σ1 + b2 (f) σ2 + ... + + bn (f) σn
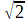 a0 (f) γ0
+ a1 (f) γ1 + a2 (f) γ2 + ... + +
an (f) γn
a0 (f) γ0
+ a1 (f) γ1 + a2 (f) γ2 + ... + +
an (f) γn+ b1 (f) σ1 + b2 (f) σ2 + ... + + bn (f) σn
On oublie volontairement les "(x)" dans cette écriture, car ce qui nous intéresse, ce ne sont plus les valeurs ponctuelles d'une fonction, mais de se la représenter globalement, comme un vecteur d'un (grand) espace.
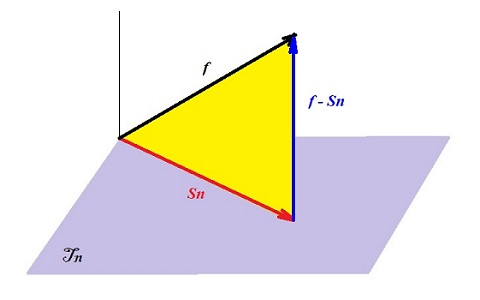 LA figure, comme aime à l'appeler votre serviteur, tant elle surclasse en
importance beaucoup d'autres...
|
La figure ci-contre représente l'espace des polynômes trigonométriques Tn , de dimension 2n+1 (n est fixé, mais quelconque), plongé dans un espace de fonctions de dimension infinie, lespace des fonctions continues par exemple, pour fixer les idées, mais on peut prendre plus grand (les fonctions intégrables). Il peut sembler téméraire de représenter cet espace par un pauvre espace à 3 dimensions, et Tn par un plan.Pourtant, cela va nous être très utile, et c'est le bon endroit pour se convaincre que, vous l'avez sûrement entendu dire, sans que cela efface votre moue sceptique: la géométrie est l'art de
raisonner juste sur des figures fausses!
Le point capital est que le triangle jaune est rectangle, ce qui revient à dire que f - Sn est orthogonale à toutes les fonctions de Tn . Et il suffit de le montrer pour tous les vecteurs d'une base: < f - Sn
, γk > = < f , γk > - < Sn
, γk >
par définition du
coefficient de Fourier.= ak (f) - < Sn , γk > Mais, cette fois d'après l'expression des composantes dans une base orthonormée, on a aussi, parce que ak (f) est la composante de Sn sur γk ak (f)
= < Sn
, γk >
Il s'en suit (avec un
calcul similaire pour les auttres membres de la base) que < f - Sn
, γk > = 0 ; < f - Sn
, σk > = 0
|
||
f ||² = || f - Sn
||² + || Sn
||²
Première conséquence: inégalité de Bessel : puisque tous les nombres écrits sont positifs,
|| Sn
||² ≤ ||
f ||² soit, en développé

Comme c'est vrai pour tout n, en résultent la convergence de la série et l'inégalité, dite de Bessel:
 |
On vient donc, avec le strict minimum d'hypothèses, et pour vraiment pas cher, de prouver la moitié de l'égalité de Parseval. Soyons honnête: c'est la moitié la plus facile, mais cela donne une première idée de la connexion entre les deux membres.
Deuxième conséquence: meilleure approximation au sens de la norme euclidienne
 LA figure,... bis! |
Reprenons et complétons notre figure. Prenons un vecteur Q quelconque, qui varie dans Tn comme si on le promenait par le bout du nez, en quelque sorte. Un nouveau triangle rectangle apparaît, correspondant à la décomposition: f - Sn
= ( f - Q ) + ( Q - Sn
)
Nous l'avons représenté en bleu. Mais n'attendons plus pour y appliquer le théorème de Pythagore!|| f - Q ||² = || f - Sn ||² + || Q - Sn
||²
Nous en déduisons || f - Q || ≥ || f - Sn || , avec égalité si et seulement si Q = Sn
|
| Autrement dit: Sn
, qui apparaissait comme projection orthogonale de f, est, parmi tous les polynômes trigonométriques de Tn , celui qui minimise la distance à f. Il est imbattable, il n'est pas possible de faire plus près que lui de f en restant dans Tn , au sens de la distance euclidienne (Mais attention: elle n'a pas de lien avec la convergence ponctuelle de la série). |
|
N.B. : Ce qui précède est le plus économique pour parvenir à ce résultat, et a l'intérêt esthétique de le faire en deux coups de cuiller à Pythagore élémentaire! Mais d'un point de vue "philosophique", il y a mieux encore. Pour former f - Sn , nous avions besoin de connaître a priori les formules donnant les coefficients de Fourier. Ce qui est phénoménal, c'est qu'on peut découvrir celles-ci en cherchant à résoudre le problème de minimisation:
Les
coefficients de Fourier s'imposent naturellement quand on cherche le
polynôme trigonométrique le plus proche de la fonction, pour la norme
euclidienne!
C'est un excellent exercice, fortememnt recommandé à tout étudiant: bien mené, le calcul ne prend que 3 lignes bien senties; il peut aussi, dans les mains d'une "brute à calcul", prendre une page complète... avant de s'enliser. Le calcul repose sur le développement bien tempéré de || f - Q ||² = < f - Q , f - Q >.
|
Indication: on peut écrire, pour éviter de distinguer les sinus et cosinus : Q = = q1 e1
+ q2 e2
+ ... + q2n+1 e2n+1
Il doit aboutir à || f - Q ||² = A(f) + ( q1 - <
f , e1
> )² + ( q2 - <
f , e2
> )² + ... + ( q2n+1 - <
f , e2n+1
> )²
La quantité A(f) ne dépend que de f,
elle donc incompressible. La somme qui suit peut alors être rendue
nulle en annulant chacun des termes, ce qui impose à chaque qk d'être le coefficient de Fourier. |
Troisième conséquence: encore plus près du but!
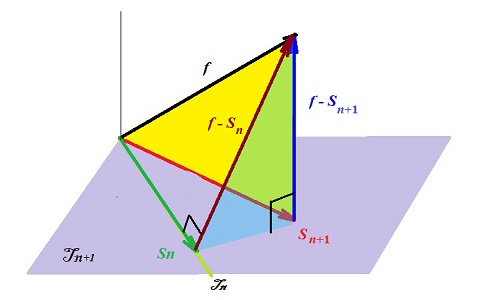 LA figure,... ter! |
Complétons encore une fois notre figure, en y montrant l'espace Tn (représenté par la droite vert pâle) comme inclus dans Tn+1 (mauve). La projection orthogonale Sn de f sur Tn , optimale dans cet espace, est un vecteur tout à fait "quelconque" dans l'espace plus grand Tn+1 , où Sn+1 fait mieux que lui! || f - Sn+1 || ≤ || f - Sn ||
Si l'on préfère -mais c'st la même chose!- cela résulte du théorème de Pythagore dans le triangle bleu translucide (qui laisse apparaître kle jaune derière lui en le teintant) || f - Sn ||² = || f - Sn+1 ||² + || Sn+1 - Sn
||²
|
| Quand n croît jusqu'à l'infini, ces distances décroissent en restant positives... donc elles ont une limite: 0 ≤ ... ≤ dn+1 = || f - Sn+1 || ≤ || f - Sn || = dn ≤ ... ≤ d0
Mais cette limite est-elle 0? Voilà la conclusion hâtive qu'il ne faut pas tirer! Il y a une limite d, le théorème des suites monotones l'affirme (dn est décroissante et minorée par 0); tout ce qu'on peut affirmer à ce stade est que d est positive ou nulle. |
|
Faire le dernier pas?
Au point où nous en sommes... ne serait-ce pas rageant de s'arrêter près d'un but qui semble si proche? Nous pouvons achever pour les fonctions continues, à condition d'admettre un résultat phare de l'analyse de Fourier. Refuser d'admettre le théorème de Parseval pour être contraint à en admettre un autre en amont, quel intérêt, penserez-vous? La question est tout à fait judicieuse (et se la poser est une saine interrogation). La raison est double: voir à l'œuvre le résultat d'approximation déduit de Pythagore d'une part, et le théorème de Fejér, présenté comme un important jalon dans notre page historique, d'autre part.
Le théorème de Fejér est une réponse à la découverte surprenante que révéla en 1873 Paul Dubois-Reymond à la communauté mathématique: la série de Fourier d'une fonction continue ne converge pas toujours! Fejér eut l'idée de considérer la moyenne des sommes partielles de Fourier; elle a un effet régulateur bienfaisant:
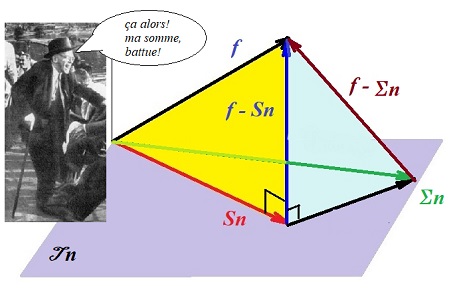 Fejér n'en revient pas: sa somme, meilleure pour la convergence ponctuelle ou uniforme, est battue quand il s'agit de la norme euclidienne |
Σn
= ( S1
+ S2
+ ... + Sn
) / n
Pour une fonction continue, elle converge uniformément vers f : || f - Σn ||u converge vers 0. Avec l'inégalité immédiate 0 ≤ || f - Σn ||² ≤ 2 || f - Σn ||u ²
la norme euclidienne || f - Σn || converge elle aussi vers vers 0. Mais Σn est dans dans Tn (moyenne d'éléments de Tn ), donc Sn est plus proche de f pour la norme euclidienne. 0 ≤ || f - Sn || ≤ || f - Σn ||
à son tour, || f - Sn || converge vers 0, par encadrement. Cest notre "deuxième conséquence" c-dessus, où nous avons pris pour vecteur Q le Σn de Fejér; ce qui revient à avoir utilisé le théorème de Pythagore (triangle bleu) || f - Σn ||² = || f - Sn ||² + || Σn - Sn
||² |
C'est déjà remarquable en soi: quoiqu'elle puisse diverger ponctuellement, la série de Fourrier converge toujours au sens de la norme euclidienne. Les combinaisons linéaires finies de sin et cos approchent uen fonction continue daussi près qu'on veut pour cette norme: on dit qu'elle sont denses dans lespace des fonctions continues, ou que le système trigonométrique est total. Voilà de quoi en faire la norme chérie de tous les utilisateurs des séries de Fourier, les "traiteurs de signal" en premier. Et revenant au triangle jaune: ||
f ||² = || f - Sn
||² + || Sn
||²
Que || f - Sn || converge vers 0 entraîne que || Sn
||² converge vers ||
f ||² , ce qui est exactement la formule de Parseval; le théorème est démontré dans le cadre choisi.
Pour des fonctions continues
par morceaux, c'est un peu plus technique, mais pas vraiment difficile.
Il faut faire de l'approximation en deux temps, de la fonction donnée
par une fonction continue, et de celle-ci par sa somme de Fourier.
|
|
Toujours plus loin ?
Il y a beaucoup de directions où poursuivre.Pour de plus en plus de fonctions: cela passe par l'invention de l'intégrale de Lebesgue, qui a permis à Frédéric Riesz d'établir une correspondance parfaite entre fonctions de carré intégrable (ce qui donne un sens au premier membre de la formule) et séries de carré sommable (ce qui donne un sens au second) : Riesz l'a résumé en une image, un billet d'aller et retour entre les deux espaces. (voir cet endroit dans notre page historique)
|
"Fatou donna à la formule de Parseval son cadre naturel, en montrant quelle est valable quand f est de carré intégrable. C'est lui qui en attribua la paternité à Parseval,
qui avait publié un mémoire en 1806, à une époque où personne en vérité
ne pouvait avoir la moindre idée de quelque chose qui ressemble à la
démonstration de la totalité du système trigonométrique. Antérieurement
à Fatou, Hurwitz avait désigné la formule comme Fundamentalsatz der Fourierischen Konstanten. [...] Hurwitz, comme nous lavons déjà dit, avait besoin de ce Fundamentalsatz pour traiter le problème isopérimétrique. Il ignorait tout, semble-t-il, des travaux antérieur [...]. "
J.-P. KAHANE. Séries de Fourier et Ondelettes
|
Cest dans l'article Séries trigonométriques et séries de Taylor (1906) aux Acta mathematica que Fatou fait cette attribution, désormais universellement retenue.
Pour d'autres systèmes orthogonaux: qu'il s'agisse des autres systèmes orthogonaux introduits par Fourier lui-même, ou pour les familles classiques de polynômes orthogaux, il est immédiat que le travail que nous avons fait jusqu'à la troisième conséquence incluse peut être décalqué à l'identique. La raison en est simple, mais elle a toute sa place dans cette page: nous n'avons utilisé que le théorème de Pythagore et celui des suites monotones!
Reste à faire ce fameux derniers pas, et, là, il n'y a plus rien de garanti; c'est à voir au cas par cas. Sturm et Liouville avaient cru y parvenir:dans la continuité de Fourier, on leur doit la première étude générale sur la question des développements en séries de fonctions orthogonales (voir notre page Liouville et l'article BibNum dédié).
Quant à la théorie des ondelettes, avatar le plus récent de celle de Fourier, elle doit pour moitié son succès à la découverte, notamment par Ingrid Daubechies, de "bons" systèmes orthogonaux (et pour l'autre, à l'adaptation de l'algorithme rapide de la FFT)
Pour les transformées de Fourier: il s'agit d'étendre le résultat aux intégrales; n'oublions pas que cet outil est encore plus prisé que les séries en traitement du signal! Mathématiquement, l'extension a été réalisée par le suisse Michel Plancherel en 1910. On a ainsi, pour toutes les fonctions intégrables et de carré intégrable,
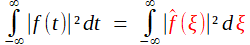 |
Au second membre, la série, qui sommait sur une infinité dénombrable de fréquences, s'est vue logiquement substituer une intégrale, sommant sur toutes les fréquences sans restriction. Cette évolution est comparable à celle que nous avons vue pour la formule dinversion (voir notre page sur la naissance de la transformation intégrale)
Sur la vie de Michel Plancherel (1885-1967) et son théorème, on trouvera plus de détails dans cet article.
Retour à l'Antique
Le problème de Didon
Exposé légendaire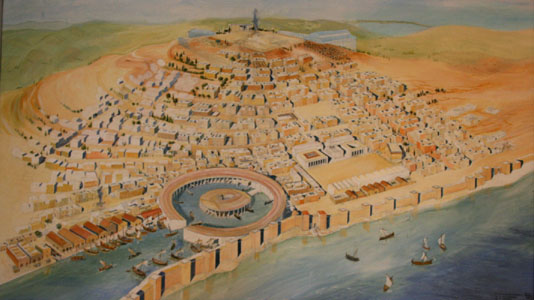 |
De Carthage aujourd'hui, il ne subsite, sinistre ironie de
l'histoire, que des ruines romaines, à de rares petits vestiges puniques près. Le forfait d'un peuple qui après avoir
vacillé devant la puissance de Cathage, décréta, par la bouche de Caton
l'Ancien, le fameux Delenda est Carthago.
Mais c'est la fondation de la ville, en 814 av. J.-C., qui nous intéresse, ou du moins sa légende. Virgile confie à Vénus le soin d'instruire incognito Énée (qui est son fils) de la terre où il vient de s'échouer, de qui la gouverne, et comment elle fut fondée: |
|
| ci-contre: image deCarthage avant la victoire de Rome, présentée sur le site archéologique ci-dessous: stèles puniques avec l'image de la déesse Tanit (sur le terrain, au Tophet) ou en forme de Tanit (au musée du Bardo, à Tunis); ruines du quartier punique de Byrsa.
|
||
|
"Tu vois ici le royaume
punique,
les Tyriens et la ville
d'Agénor ;
mais il s'agit du territoire des Libyens, peuple intraitable à la guerre. Didon y exerce le pouvoir ; elle est partie de la ville de Tyr, fuyant son frère. Longue suite d'injustices et de vicissitudes ![...] À Tyr régnait son frère Pygmalion, le plus scélérat des hommes. [...] [lequel assassine son mari, par cupidité]
Mais, dans son sommeil, elle vit l'image
même de son époux,privé de sépulture et qui levait vers elle un visage étrangement pâle ; Il parle de l'autel ensanglanté, dénude sa poitrine transpercée par le fer, et dévoile point par point le crime, resté secret, de sa maison. Puis il la persuade de fuir au plus vite, de quitter sa patrie. Pour l'aider dans son voyage, il révèle où sont enfouis en terre d'anciens trésors, masse ignorée d'or et d'argent. |
Virgile, entre les muses Clio et Melpomène Musée du Bardo, Tunis |
sur un billet tunisien, sous son autre nom, Elyssa |
Émue, Didon préparait
sa fuite, cherchait des compagnons.
Autour d'elle se rassemblent ceux qui vouaient au tyran une haine féroce ou qu'habitait une grande crainte ; des bateaux qui se trouvaient prêts, ont pris d'assaut et on y entasse l'or ; la mer emporte les trésors de l'avide Pygmalion ; c'est la femme qui dirige tout. Les fugitifs parvinrent en ces lieux, où tu vois maintenant d'immenses remparts et la citadelle naissante de la jeune Carthage, qui s'appelle Bursa du fait qu'ils ont acheté comme surface de terrain juste la quantité qu'ils pouvaient entourer avec la peau d'un taureau." |
par Giovanni Pittoni (1687-1767) au Musée de l'Ermitage, St Pertersbourg (Russie) |
par Matthias Merian l'Ancien (1687-1767)
|
Les seigneurs de l'endroit pensaient avoir roulé la princesse en lui vendant fort cher une parcelle dérisoire... mais la rusée Didon découpa la peua en fines lanières (comme le montrent les images), de façon à entourer le plus grand domaine possible. Car, une fois fabriquée une liongue corde par son subterfuge, restait à résoudre un ropblème d'optimisation mathématique:
Étant donnée une corde de longueur L, quelle forme lui donner pour quelle entoure la plus grande surface possible?
Petites expériences pour se familiariser
1. Parmi les rectangles de périmètre L donné, c'est le carré qui donnera le meilleur résultat, S = L²/16 (facile)
2. Parmi les triangles de périmètre L donné, c'est le triangle équilatéral qui donnera le meilleur résultat, et 27 S² = L4/16.
Un peu moins facile, déjà! Utiliser la formule de Héron d'Alexandrie, où p = L / 2 est le demi-périmètre:
- S² = p.(p - a). (p - b)..(p - c).
3. La comparaison des deux donne un avantage au carré sur le triangle équilatéral... que se passe-t-il pour les polygones réguliers?
On trouvera avec un petit dessin, ou... dans l'article Wikipedia comment exprimer périmètre et surface en fonction du rayon du cercle circonscrit R et du nombre de côtés n
L = 2R .n sin π/n ; S = ½ R .L cos π/n
.dont on déduit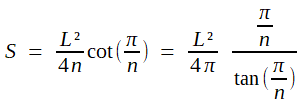
Cette surface croît en fonction de n, car par composition, tout se ramène à la croissance de la fonction (tan x)/x, facile à vérfier par dérivation. On a donc intérêt à augmenter indéfiniment le nombre de côtés... jusqu'au cercle!
On notera que le cercle apparaît bien comme cas limite, et qu'on a par ailleurspour tous les polygones réguliers 4πS ≤ L² (inégalité isopérimétrique)
Alors, Didon... intuition féminine ou intuition géométrique? L'argument des polygones était certes suffisant pour qui veut tracer le contour des fortifications d'une ville; il ne saurait suffire à un mathématicien. Il va appeler Parseval à sa rescousse!
Quand Parseval vole au secours de Didon
Quelques lignes suffisent pour
déduire le cas le plus général du théorème de Parseval: cette élégante
démonstration a été proposée en 1901 par Adolf Hurwitz
(1859-1919). Elle ne demande de connaître, pour la comprendre, que les
formules intégrales donnant la longueur d'une courbe et maire qu'elle
enferme.1. Considérons une courbe fermée de classe C1, c'est à dire continue et dont la tangente varie, elle aussi, continûment, sans heurt. Elle peut être paramétrée, au moins théoriquement -et c'est ce qui nous occupe- par son abccisse curviligne s, et sa longiueur est L.Si vous n'êtes pas familier de ces notions, imaginez simplement que vous avez disposé une corde le long de la courbe, puis que vous la tendez: sa longueur est L, et s mesure la position entre 0 et L!on a rectifié la courbe (ici, au sens propre, matériel), c'est le mot qu'emploie les mathématiciens, qui se contentent pour leur part d'une vue de l'esprit..
Pour utiliser l'analyse de Fourier, on se ramène à l'intervalle [0, 2π] par le (petit) changement de paramètre t = 2πs / L; on appelle alors x(t) et y(t) les coordonnées d'un point courant.Notons que les hypothèses faites rendent x(t) et y(t) sommes de leurs séries de Fourier respectives (grâce au théorème de Dirichlet -voir notre page historique), alors que rien ne permet de le dire pour leurs dérivées x'(t) et y'(t) ; mais de toutes façons, nous n'aurons aucun besoin de développements pour ce qui suit, juste du théorème de Parseval, qui ne nécessite que les coefficients de Fourier.
| fonction |
x |
y | x' | y' |
| coeff. de cos nt |
an | cn | αn = n bn |
γn = n dn |
| coeff. de sin nt | bn | dn | βn = - n an | δn = -n cn |
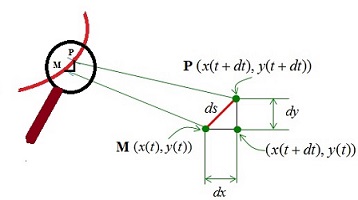
2. La suite va utiliser d'abord le "triangle rectangle infinitésimal" de Leibnitz évoqué plus haut, c'est à dire essentiellement la relation
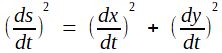 ou, avec s :
ou, avec s : 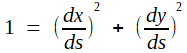
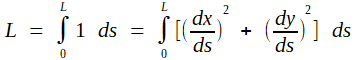
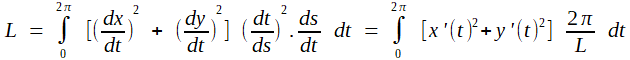
ce qui permet d'appliquer le résultat de Parseval aux fonctionx continues x' et y'
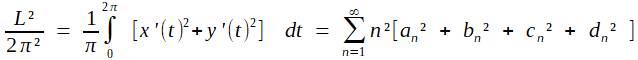 (P1)
(P1)3. Par ailleurs, l'aire S délimitée par la courbe s'exprime; selon une des classiques formules déduites du théorème de Green-Riemann, par
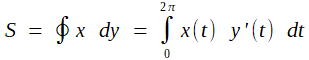
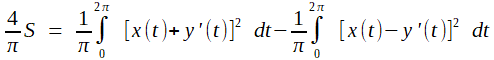
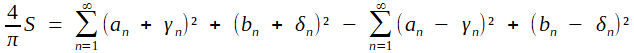 (P2)
(P2)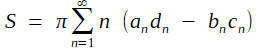
à partie de la majoration immédiate
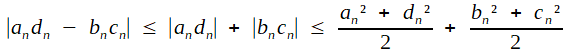
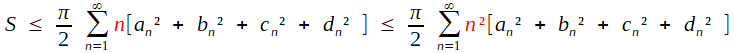 (I)
(I)| 4πS ≤ L² (inégalité isopérimétrique) |
L'égalité exige donc que tous les coefficients pour n>1 soient nuls.
Si oui, en reprenant la chaîne des inégalités -qui doivent toutes devenir des égalités- on a aussi a1 = d1 , b1 = - c1. Le paramétrage est clairement celui d'un cercle, qui convient effectivement à l'égalité.
| 4πS = L² si et seulement si la courbe est un cercle. |
Si vous avez la curiosité de regarder son article original (aucun peoblème, il est en Français!), vous verrez d'ailleurs que nous n'avons pas fait très original... p401, p402, p403.
 |
 |
|
| Hurwitz en 1910 (Wikipedia) |
Volume et début de l'article (CRAS 1901); source: Gallica BnF | |
Le problème isopérimétrique en lui-même est très intéressant, et il a une longue histoire... inachevée, car le cas de la dimension 2 se généralise mal aux dimensions supérieures (pour ne donner qu'une image élémentaire, le cercle est approché par les polygones réguliers, mais cest impossible pour la sphère, car il n'ya que les 5 solides pythagoriciens évoqués plus haut!). La première approche sérieuse est est celle de Steiner en 1836; mais elle est incomplète sur l'existence; cette lacune ne sera comblée qu'en 1895 par Minkowski et Weirstrass. Les idées de Steiner, à la fois élémentaires et ingénieuses, sont très clairement présentées en cinq minutes chrono dans cette vidéo proposée par le Centre Henri Lebesgue: c'est la règle du jeu de la série des "5' de Lebesgue".
On peut consulter comme points d'entrée les articles isopérimétrie et théorème isopérimétrique de Wikipedia, , celui du site Cut the Knot: Isoperimetric Theorem and Inequality, et la famille d'articles de Jennifer Wiegert The Sagacity of Circles: A History of the Isoperimetric Problem (site de la MAA)
Pour une étude plus fouillée mathématiquement, mais qui exige plus de son lecteur:
- Arnaud Duran, Inéegalités géométriques dans le plan euclidien (TER, 2006)
- Marine Malo, CoralieRenault, Inégalité Isopérimétrique (mémoire ENS Cachan, 2012)
Références
Du côté de Pythagore
- B. ARTMANN, Euclid. The Creation of Mathematics (Springer)
- P. BREMAUD, Le Dossier Pythagore (Ellipses)
- O. BYRNE, The Elements of
Euclid (W. Pickering 1847; en fac
simile: Taschen 2010) ou en ligne ici.
- H. CHARDAK, L'Énigme Pythagore (Presses de la Renaissance)
- JAMBLIQUE, Vie de Pythagore (Les Belles Lettres), voir des liens vers les éditions latines en ligne.
- DIOGÈNE LAËRCE, Pythagore in Vie des Philosophes Illustres (trad. 193)
- E. LOOMIS, The Pythagorean
Proposition: Its Demonstration Analyzed and Classified (en
ligne sur Archive.org)
- E. MAOR, The Pythagorean Theorem (Princeton University Press)
- PORPHYRE de TYR, Histoire de la philosophie (vers 260) : fragments, Vie de Pythagore. Lettre à Marcella ( Les Belles Lettres)
Du côté de Parseval
- S.F. LACROIX, Traité des différences et des séries ( sur e|rara, ETH Zurich)
- M.-A. PARSEVAL in Mémoires présentés
à l'Institut des Sciences, Lettres et Arts: 1805 (sur
Google Books)
Du côté de Fourier
- B. BURKE-HUBBARD, Ondes et Ondelettes (Belin-Pour la Science)
- C. GASQUET, P.WITOMSKI, Analyse de Fourier et Applications (Dunod)
- J.-P. KAHANE, P.-G. LEMARIÉ, Séries de Fourier et Ondelettes (Cassini)
Poursuivre dans le Monde de Fourier...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Revenir à la Page Biographique