avec un portrait conservé à l'École Polytechnique
 |
 |
| Arrivée au Panthéon | |
 |
 |
| Entrée au Panthéon | |
 |
 |
 |
| Dépôt de la gerbe... et salut au premier professeur d'Analyse de l'École Polytechnique | ||
 |
 |  |
| Mais qu'y a-t-il sur le ruban? | Ah, oui, bien sûr! L'équation d'Euler-Lagrange... | ... qu'on retrouve sur le mug commémoratif! |
 |
 |  |
| " | "Après m'être longtemps et inutilement fatigué à chercher cette intégrale, quel a été mon étonnement lorsque j'ai appris que dans les Mémoires de Turin le problème se trouvait résolu avec autant de facilté que de bonheur. Cette belle découverte m'a causé d'autant plus d'admiration qu'elle est plus différente des méthodes que j'avais données et qu'elle les surpasse considérablement en simplicité." L. Euler
|
|
 |
 |
| Le discours d'hommage, par Jérôme Perez, organisateur de la manifestation. | |
 |
 |
|
«Lagrange, le premier des savants d'Europe, paraît avoir de 50 à 60 ans: il est cependant plus jeune; il a dans les traits de la dignité et de la finesse dans la physionomie; il paraît un peu grêle et pâle; sa voix est très faible, à moins qu''il ne s'échauffe; il a l'accent italien très marqué et prononce les s comme des z; il est très modestement vêtu en noir ou en brun; il parle très familièrement et avec quelque peine; il a dans la parole l'embarras et la simplicité d'un enfant. Tout le monde voit bien que c'est un homme extraordinaire, mais il faut l'avoir vu pour y reconnaître un grand homme. Il ne parle que dans les conférences, et il y a telle de ses phrases qui exciterait la risée. Il disait l'autre jour: "Il y a encore sur cette matière beaucoup de choses importantes à dire, mais je ne les dirai pas. " Les élèves, dont la plupart sont incapables de l'apprécier, lui font assez peu d'accueil, mais les professeurs le dédommagent.» Notes manuscrites de Joseph FOURIER |
 |
 |
 |
|
| "Joseph Louis Lagrange est né dans cette maison le 25 janvier 1736" "Par décret de la commune" |
|
|
«Son père était riche, il avait fait un mariage avantageux, mais il s'était ruiné dans des entreprises hasardeuses. N'en plaignons pas M. Lagrange. Lui-même envisageait ce malheur comme la première cause de tout ce qui lui était arrivé ensuite de plus heureux. S'il avait eu de la fortune, a-t-il dit lui même, il n'eût probablement pas fait son état des Mathématiques [...]» J.-B. Delambre, Notice sur la Vie et les Ouvrages de M. le Comte J.-L. Lagrange, in Œuvres, t1. |
 |
| 
|
| Le couchant est un autre moment favorable, quand le soleil illumine par ses reflets les vitres du bâtiment latéral: |  |
|
 |
 |  |
| Notez la dédicace sur le socle: "à Luigi Lagrange, la Patrie" |
||
 |
 |
 |
 |
|
Le premier article qu'il y publie, en 1759, a trait aux conditions suffisantes pour qu'une fonction de plusieurs variables possède un extremum
en un point où ses dérivées partielles premières s'annulent (condition
nécéesssaire qui traduit l'annulation de la dérivée pour chacune des
fonctions d'une variable, prise en fixant toutes les autres)
Il présente le cas de deux variables, en réduisant sur la forme quadratique, comme on l'enseigne encore aujourd'hui en prépa et en premier cycle universitaire. article complet: Œuvres, t1 (sur Gallica) |
 |
 |
| "Ce télescope a été envoyé au point Lagrange 2; c'est un endroit très stable, idéal pour les observations précises; c'est là aussi que se trouve le télescope spatial James Webb." |
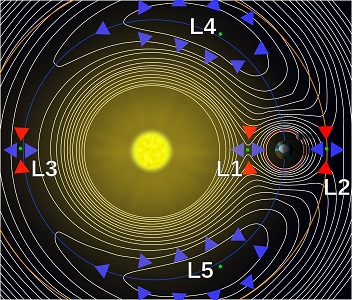
| Les points de Lagrange de deux planètes
sont des points où leurs attractions respectives (sur un
troisième corps, un satellite par exemple) se compensent exactement. Il
y a donc autant de systèmes de points de Lagrange que de couples de
planètes; ceux qui vont nous intéresser sont ici ceux du système
Soleil-Terre, mais il y en a aussi pour le système Terre-Lune, pour le
système Soleil-Jupiter (comme on le verra ci-dessous), etc... ce sont
donc des points d'équilibre
du champ de gravitation auquel est soumis le satellite. Il est temps de
regarder où ils se trouvent! L'image ci-contre nous les montre. Le plus évident intuitivement est sans doute L1: on conçoit facilement qu'en se déplaçant en ligne droite entre les deux masses attractives, il existe un point où l'influence de la première cesse d'être prédominante au profit de la seconde. Mais il en existe deux autres sur cette ligne, à l'extérieur du segment des deux masses; L2 est justement un de ces deux points. Ces trois premiers points ont en fait été mis en évidence par Euler, et le mérite de Lagrange est d'avoir découvert les deux derniers, L4 et L5, qui forment avec L3 un triangle équilatéral, raflant ainsi la mise de l'appellation. |
 timbre allemand, de réalisation personnelle (source) |
 |
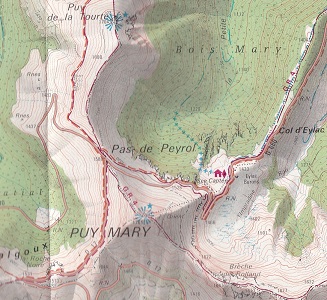 | Une situation géographique analogue, sur une carte de randonnée (col du Pas de Peyrol, au voisinage du Puy Mary, Cantal) |
Vision tridimensionnelle de la situation géographique analogue. En un col, il y a pour l'altitude un minimum sur la courbe jaune, joignant deux sommets, mais un maximum pour la ligne joignant deux vallées. Le modèle mathématique le plus simple est un paraboloïde hyperbolique (modèle el plâtre, collection de l'IHP); détails à voir dans notre page sur cette belle surface. |  |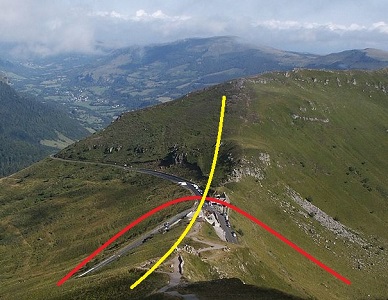
 |
Les anglo-saxons préfèrent l'appellation point-selle (saddle-point), fort évocatrice... Le Mathouriste
n'a pas hésité à se rendre à Fort Worth,Texas pour vous offrir cette
image d'une selle de 1847 qui confirme la pertinence de la dénomination.
Un point-selle est instable:
une bille posée en ce point, à la moindre pichenette, au moindre
souffle, partira dans l'une ou l'autre des vallées. Dans l'espace, L1, L2
et L3 sont tous des équilibres instables:
le plus petit écart d'un satellite qui s'y trouverait le ferait
basculer sous l'influence gravitationnelle prépondérante, soit de la
Terre, soit du Soleil.
|
 |
|
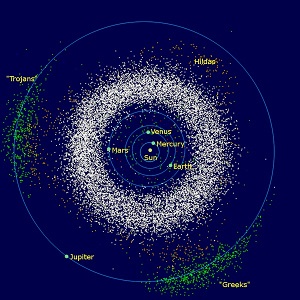 Les astéroïdes Troyens (source: Wikipedia) | En revanche, les points L4 et L5 sont toujours stables; une manifestation bien concrète se montre dans le système Soleil-Jupiter, où deux "paquets" d'astéroïdes, dénommés Troyens, se regroupent au voisinage de L4 et L5, Peut-être ont-ils "voyagé" auparaavant, mais une fois piégés à cet endroit, ils n'ont plus l'énergie pour s'en extraire, et une petite perturbation n'aura aucun effet notoire; ils seront naturellement ramenés dans cette zone. On a dénombré, en 2023, 7 079 troyens de Jupiter, dont 4 603 au niveau du point de Lagrange L4 (dit camp grec) et 2 476 au niveau du point de Lagrange L5 (dit camp troyen). C'est qu'en effet, le premier découvert (par Max Wolf, en 1906) avait été baptisé... Achille, grec notoire! S'en suivit l'idée de les nommer d'après l'Illiade, en les répartissant en Grecs et Troyens. Le système Soleil-Terre en possède aussi, mais les deux premières découvertes sont très récentes, et les noms qui leur ont été attribués (provisoirement?) ne feront pas rêver les amateurs de mythologie: 2010TK7 (L4, en 2011), 2020XL5 ((L4, en 2021). |
 |
 |
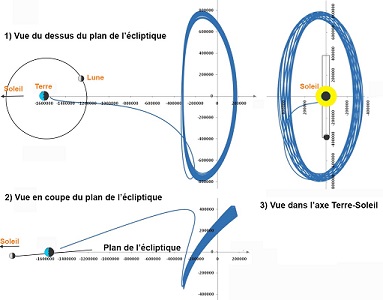 (source: Wikipedia) | Voici, à titre d'exemple, la trajectoire de James Webb, depuis la Terre jusqu'à L2 et autour... un régal pour amateurs de géométrie descriptive, avec ses 3 vues (en correspondance 2 à 2) sur des plans de références perpendiculaires! Si on prend la peine d'y réfléchir, L2, point instable, a, malgré les apparences immédiates, plus d'avantages que d'inconvénients pour y installer un engin d'observation: l'absence d'astéroïdes au voisinage (qui est une conséquence de cette instabilité) diminue le risque de collision qui pourrait endommager le satellite et ses appareils -cauchemar récurrent des équipes qui surveillent le bon déroulement du vol- et de surcroît, L2 est toujours dans l'ombre de la Terre, donc le Soleil ne perturbe pas l'observation et la photographie des lointaines galaxies. Qui plus est, le Soleil ne se trouve ainsi jamais entre le satellite et la Terre, ce qui assure d'excellentes communications, garantes de l'intégrité des données transmises. |
| Le point de Lagrange L2 du système Soleil-Terre avait édéjà été utilisé par les satellites Herschel et Planck ;
tous deux ont fini leurs missions en 2013, et, grâce à l'absence
volontaire de correction de trajectoire, ont glissé naturellement hors
du voisinage. Autant libérer la zone le plus possible avant d'y envoyer
d'autres engins. Un troisième observatoire y était en place avant James Webb et d'Euclid. Lancé par l'ESA comme ce dernier, il a pour nom Gaïa, et navigue plus près de L2 , sur une orbite de Lissaajous (Salut à toi, Jules!) 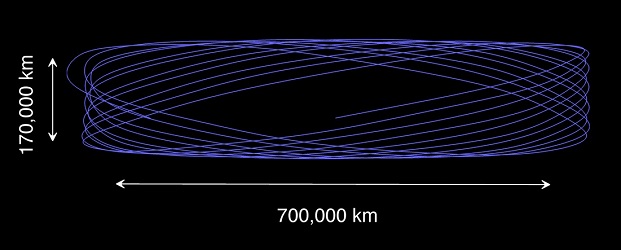 Orbite de Gaïa, vue de la Terre. (sur le site de l'ESA) Elle s'inscrit dans un rectangle, c'est "typiquement Lissajous"! Un quatrième devrait les rejoindre en 2027, le Nancy Grace Roman Space Telescope. |
 capture
d'écran faisant clairement voir les orbites de J. Webb (bleue), Euclid
(verte) et Gaïa (jaune) ayutour de . Image à agrandir par clic.
Voir l' Animation vidéo réalisée par l'ESA, sur YouTiube |
||||
|
En revanche L1 est une position intéressante, entre Soleil et Terre, pour étudier l'étoile qui nous éclaire et nous chauffe: on y a donc placé le satellite d'observation SoHO.
Placer un télescope spatial au point L4 ou L5 du système Terre-Lune? Cela a été envisagé,
mais des nuages de poussière y ont été observés (accumulation provoquée
par la stabilité de ces points...), si bien que le projet a été
abandonné: illustration concrète de l'avantage, tout bien pesé,
d'un point instable sur un point stable!
La science-fiction en a également tiré parti: Dans la "suite" donnée par Peter Hyams: 2010, l'Année du Premier Contact au mythique 2001, l'Odyssée de l'Espace de Stanley Kubrick, le vaisseau Discovery est garé en orbite à un point de Lagrange du système formé par Jupiter et son satellite Io. Rendez-vous chez Lagrange, donc, encore une fois, pour savoir où en est le pervers ordinateur HAL -qui, a n'en point douter, faisait preuve de plus d'Intelligence Artificielle que ChatGPT, sauf que l'expression n'était pas encore dévoyée, à l'époque de Stanley Kubrick.
|
|||||
 |
 |  |
