Clairaut, Night and Day...
C'est
à l'Hôtel de Ville de Paris que l'on peut s'offrir
cette évocation
à la Cole Porter: que dire de mieux
à un astronome, certes unique?
"Night and day, you are the one
Only you beneath the moon and under the sun
Whether near to me or far..."
Only you beneath the moon and under the sun
Whether near to me or far..."
(A sa
place, l'auteur de ces lignes se le ferait chanter par Ella... mais si vous
le préférez dansé par Ginger et Fred,
pourquoi pas!)
Plus
précisément,
si vous la cherchez, la statue est située sur la face
arrière du bâtiment (donnant sur la rue de Lobau,
perpendiculairement à la rue de Rivoli). Il ne vous restera
plus
qu'à lever les yeux, elle est au troisième
étage
de niches...
| Hôtel de Ville, Paris (côté rue de Lobau) | |
Alexis Clairaut
(1713-1765) est d'ailleurs né et mort dans cette ville. 2013
a
vu commémorer le tricentenaire de sa naissance, et Mai 2015
se
situe 250 ans après son décès. Des
occasions pour
ne pas oublier un savant des Lumières, un des plus important
de son époque.
Mathématicien
On n'exagérerait guère en disant que Clairaut a têté les Mathématiques au biberon: son père est mathématicien, il apprend à lire à 4 ans dans les Éléments d'Euclide, publie sa première recherche à 12 ans et 8 mois et entre à l'Académie Royale des Sciences à l'âge de 18 ans, par dérogation royale: l'âge minimum requis était 21 ans! Il restera ainsi le plus jeune académicien de tous les temps. Il a gagné cette place grâce à un mémoire sur ce que l'on appelle aujourd'hui les courbes gauches (courbes de l'espace qui ne sont pas planes): il les nomme à double courbure en faisant référence à deux de leurs projections sur les plans de référence, puisque chacune a sa courbure propre (La notion, pour les courbes planes, de rayon de courbure est plus intuitive, donc plus facile pour un premier contact). De nos jours, on utilise toujours deux paramètres dans l'étude métrique locale de la courbe, la courbure et la torsion. Personne avant lui n'avait abordé cette question.
On lui doit aussi la démonstration du résultat annoncé par Newton dans sa classification des cubiques (Enumératio Linearum Tertii Ordinis, 1706): elles peuvent toutes être considérées comme projections coniques du modèle
C'est un fait capital dans la théorie moderne des courbes elliptiques (cryptographie, Grand Théoème de Fermat), qui ramène les 72 espèces de Newton à 5 types seulement!
qu'il a laissé son nom de façon la
plus durable en
Mathématiques.
Pourtant, celle-ci n'apparait, pour la première fois, qu'au détour d'un mémoire de géométrie où il s'agit de construire des courbes satisfaisant à des propriétés diverses; le dernier problème est de déterminer une courbe enveloppée (c'est le mot exact!) par un mouvement d'équerre dont le sommet décrit une courbe donnée.
L'ensemble est plutôt touffu, mais avant de passer à des exemples, Clairaut mentionne plus explicitement le cas d'une équation différentielle qui, à côté d'une famille de droites solutions, a en plus une parabole solution. Et pour cause: les droites solutions forment la famille des tangentes à cette parabole; en chaque point, le triplet (x, y, y') est donc le même pour la parabole et sa tangente: s'il vérifie l'équation pour l'une, il la vérifie pour l'autre. Mais pour prouver qu'elle est solution, la parabole, en chaque point, requiert l'aide d'une solution "droite" différente!
Hélas...aussi, elle est universelle; autrement dit, sa merveilleuse simplicité est le germe d'une fabuleuse complexité! C'est que "tout le monde attire tout le monde"; et l'ellipticité des orbites n'est prouvée qu'en considérant que le soleil est seul avec chacune des planètes, ce qui est bien sûr faux en théorie. La Terre, par exemple, subit aussi l'attraction de:
Mais il en va tout autrement de la Lune avec la Terre: l'imposante masse du soleil empêche d'en négliger l'action. Le système Terre-Lune-Soleil est une instance du célèbre problème des trois corps; et comme au théâtre de boulevard, le ménage à trois s'avère extrêmement compliqué avec un ressort très simple (ici, la loi de Newton).
Clairaut est un pionnier de ce sujet, et, après avoir, dans un premier temps, douté de la loi de Newton au point d'envisager l'ajout d'un terme complémentaire en 1/r4, il considère l'action du soleil comme une force perturbatrice (On reste donc proche du théâtre!): l'idée est d'introduire la correction nécessaire dans les équations et d'en déduire une correction correspondante de l'ellipse.
Effectivement, comme nous le rappelle Poisson, Clairaut maîtrisait bien le système (différentiel) exact du problème des trois corps. Mais il avait assez vite renoncé à en obtenir des formules explicites de solution -on sait depuis Poincaré qu'une telle recherche serait illusoire. Après avoir posé explicitement les six équations différentielles, Clairaut dit:
Les comètes "de 1531,1607,1682" étaient soupçonnées d'être un seul et même objet, réapparaissant avec une période de 76 ans: on l'attendait donc pour 1758. Mais, l'orbite étant une ellipse très allongée (ce qui explique que les retours soient très espacés), Clairaut pense qu'elle doit subir les perturbations des planètes massives connues, Jupiter et Saturne, et recalcule la trajectoire d'une façon semblable à son travail sur la lune. Il se fait aider du jeune Jérôme Lalande, et prédit un retour retardé par les perturbations, pour Mars 1759. Elle arrive en Avril, c'est un triomphe pour les deux hommes... et la théorie de Newton.
Le premier mérite une attention toute particulière: publié en 1753, il a été conçu entre 1734 et 1736, à partir des cours d'initiation qu'il donna à la marquise Émilie du Châtelet. Aussi avide de connaissances que... des hommes qui pouvaient les lui apporter -et qui étaient fort bien choisis!- elle avait quelque peu lassé Maupertuis en le pressant de passer aux... travaux pratiques; et celui-ci n'avait pu faire lever le siège qu'en la confiant à Clairaut. Si l'on en croit un Diderot quelque peu persifleur (mais peut-être voulait-il railler le rival de son ami d'Alembert dans la théorie lunaire...), cela ne lui aurait pas déplu:
La matière en est élémentaire, mais laissez l'académicien Etienne Ghys vous convaincre, en fin connaisseur, que "c'est une petit merveille" qui en remontrerait à bien des manuels (et des programmes scolaires!) d'aujourd'hui dans sa manière de démontrer -serait-ce au prix d'un escamotage provisoire (pour ne pas perturber le lecteur) sur lequel on revient plus tard, dans sa façon d'aborder les problèmes, de susciter le questionnement... Faut-il le préciser, cette présentation est à la portée de non spécialistes, qui découvriront avec surprise et ravissement qu'on peut montrer le théorème de Pythagore à l'aide de jolis découpages (pratiqués par les Chinois bien antérieurement, soit dit au passage)
"Il est temps de de le remettre
à sa vraie place, parmi les plus grands"
J.-P. KAHANE, Introduction aux conférences du
Tricentenaire (Mai 2013)
Mathématicien
Géométrie d'abord...
| Premier exploit... |
|
On n'exagérerait guère en disant que Clairaut a têté les Mathématiques au biberon: son père est mathématicien, il apprend à lire à 4 ans dans les Éléments d'Euclide, publie sa première recherche à 12 ans et 8 mois et entre à l'Académie Royale des Sciences à l'âge de 18 ans, par dérogation royale: l'âge minimum requis était 21 ans! Il restera ainsi le plus jeune académicien de tous les temps. Il a gagné cette place grâce à un mémoire sur ce que l'on appelle aujourd'hui les courbes gauches (courbes de l'espace qui ne sont pas planes): il les nomme à double courbure en faisant référence à deux de leurs projections sur les plans de référence, puisque chacune a sa courbure propre (La notion, pour les courbes planes, de rayon de courbure est plus intuitive, donc plus facile pour un premier contact). De nos jours, on utilise toujours deux paramètres dans l'étude métrique locale de la courbe, la courbure et la torsion. Personne avant lui n'avait abordé cette question.
On lui doit aussi la démonstration du résultat annoncé par Newton dans sa classification des cubiques (Enumératio Linearum Tertii Ordinis, 1706): elles peuvent toutes être considérées comme projections coniques du modèle
| y2 = x3 + px + q |
C'est un fait capital dans la théorie moderne des courbes elliptiques (cryptographie, Grand Théoème de Fermat), qui ramène les 72 espèces de Newton à 5 types seulement!
L'équation de Clairaut
Mais c'est grâce à l'équation différentielle| y = x y' + f (y') |
Pourtant, celle-ci n'apparait, pour la première fois, qu'au détour d'un mémoire de géométrie où il s'agit de construire des courbes satisfaisant à des propriétés diverses; le dernier problème est de déterminer une courbe enveloppée (c'est le mot exact!) par un mouvement d'équerre dont le sommet décrit une courbe donnée.
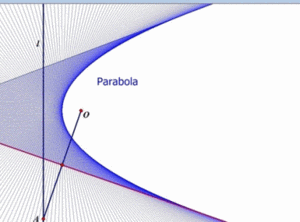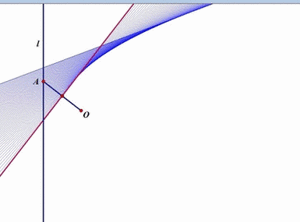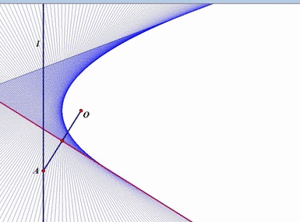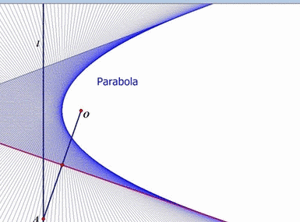
L'ensemble est plutôt touffu, mais avant de passer à des exemples, Clairaut mentionne plus explicitement le cas d'une équation différentielle qui, à côté d'une famille de droites solutions, a en plus une parabole solution. Et pour cause: les droites solutions forment la famille des tangentes à cette parabole; en chaque point, le triplet (x, y, y') est donc le même pour la parabole et sa tangente: s'il vérifie l'équation pour l'une, il la vérifie pour l'autre. Mais pour prouver qu'elle est solution, la parabole, en chaque point, requiert l'aide d'une solution "droite" différente!
|
Comme le montre l'animation
ci-contre (source: Math Images), la parabole apparait
sans être jamais dessinée elle-même:
il a suffi de tracer sa famille
de tangentes pour la faire apparaître!
C'est
exactement ce qui se passe pour notre exemple d''équation de
Clairaut: les droites solutions "dessinent une nouvelle
solution"
parabolique.
|
 |
Traiter
l'exemple du texte, aujourd'hui:
2/ On cherche les solutions de classe C² (deux fois continûment dérivable) On peut alors dériver l'équation ; on obtient: y". ( x + 1 - 2 y' )
= 0
Les
droites solutions sont retrouvées avec y" = 0.
Mais il y a clairement une autre possibilité, x + 1 -2 y' = 0; que vérifie y = (x + 1)² / 4 3/ Des solutions "composites", de classe C1 , peuvent être formées par réunion des précédentes: un arc de parabole et ses deux tangentes. 4/ On peut montrer qu'il n'y en a pas d'autres (attention, c'est un peu plus délicat dans le traitement du produit, ci-dessus!) |
Astronome
Night (and Day): la nuit est propice à l'observation de la lune et des comètes. Mais Clairaut n'est pas un astronome au sens: observateur assidu. C'est plutôt un Mécanicien céleste, qui va développer les mathématiques de la prévision du mouvement des astres, comme l'ont fait avant lui Copernic et Kepler, comme le feront plus tard Laplace et Leverrier.La Lune
La magnifique simplicité de la loi d'attraction de Newton, proportionnelle aux masses et inversement proportionnelle au carré de la distance mutuelle, assigne, en première vision, à chaque planète une orbite elliptique autour du soleil qui l'attire. Encore plus magnifique, elle est universelle... donc s'applique aussi bien à la lune autour de la terre.Hélas...aussi, elle est universelle; autrement dit, sa merveilleuse simplicité est le germe d'une fabuleuse complexité! C'est que "tout le monde attire tout le monde"; et l'ellipticité des orbites n'est prouvée qu'en considérant que le soleil est seul avec chacune des planètes, ce qui est bien sûr faux en théorie. La Terre, par exemple, subit aussi l'attraction de:
- Mercure, Vénus, Mars, relativement proches mais heureusement de masse très faible devant celle du soleil, ce qui permet de négliger leur effet;
- Jupiter, la plus massive, mais heureusement assez lointaine pour pouvoir négliger son effet;
- Saturne, Uranus, Neptune, moins massives et plus loin que Jupiter...
Mais il en va tout autrement de la Lune avec la Terre: l'imposante masse du soleil empêche d'en négliger l'action. Le système Terre-Lune-Soleil est une instance du célèbre problème des trois corps; et comme au théâtre de boulevard, le ménage à trois s'avère extrêmement compliqué avec un ressort très simple (ici, la loi de Newton).
Clairaut est un pionnier de ce sujet, et, après avoir, dans un premier temps, douté de la loi de Newton au point d'envisager l'ajout d'un terme complémentaire en 1/r4, il considère l'action du soleil comme une force perturbatrice (On reste donc proche du théâtre!): l'idée est d'introduire la correction nécessaire dans les équations et d'en déduire une correction correspondante de l'ellipse.
| Toutes les pages en photos sur le site e-rara (ETH Zürich) |
| En quoi Clairaut innove-t-il? | ||||||||
Les
équations d'un mouvement à force centrale
se ramènent classiquement, en
éliminant le temps, à une relation entre l'angle
θ
etle rayon-vecteur r,
considéré comme fonction de l'angle θ, ce
qui suffit à déterminer la trajectoire (mais pas,
bien
sûr, la façon dont elle est parcourue). Il est
plus simple
d'utiliser la fonction u(θ)= 1/ r(θ),
c'est la célèbre formule
de Binet:
|
||||||||
| Deux corps | Trois corps | |||||||
| Γ = - ku²(θ)
, puisque l'attraction est en 1/
r². L'équation se simplifie remarquablement, au point de devenir linéaire!
|
Γ = - ku²(θ)
+ Γ1
, avec un terme complémentaire (non
constant, compliqué) puisqu'une autre force s'exerce depuis
le soleil. Finie, la belle simplification providentielle!
ce que
Clairaut écrit, ne retenant que la forme
générale
Ω est
toujours aussi compliqué...
... mais c'est là qu'il a une idée formidable: Si Ω peut s'écrire sous la forme d'une somme de termes
une solution s'écrira -comme apprend à le faire tout étudiant de première année- en ajoutant à celle de gauche la quantité
On a ici les prémisses d'une Analyse de Fourier! (à ceci près qu'elle est limitée à un problème spécifique) Somme finie ou série? La diffuculté mathématique n'est certes pas la même; mais en pratique, les astronomes travaillent toujours avec des développements tronqués, soit des sommes finies. Ce qui rend triviale la légitimté de la formule solution; ce qui compte, c'est la légitimité des approximations initiales. Techniquement, obtenir ce développement -en fait, limité- exige donc de l'attention, du doigté -comment ramener tout en fonction de θ, que négliger, que conserver... C'est assez long, mais Clairaut y réussit avec brio. |
|||||||
Voici ce
passage en version originale; noter l'allusion au "célèbre
M. Euler",
et la quantité initiale au début du lemme 2,
qu'on lirait
de façon moderne comme l'expression issue de la
méthode
de variation des constantes (dont ceci est une preuve d'existence avant
Lagrange!).
Elle est obtenue de façon un peu mystérieuse,
et l'employer est plus compliqué (il faut
linéariser,
mais heureusement, les géomètres
connaissent bien leurs formules de trigo, eux!) qu'intégrer
les seconds membres particuliers.
| pages issues du site e-rara (ETH Zürich) | |
| "Clairaut
est le premier qui ait donné une théorie du
mouvement de
la Lune, fondée sur l'intégration, par des
séries,
des équations différentielles du
problème des
trois corps, qu'il avait obtenu en même temps qu'Euler et
d'Alembert." Denis
Poisson, Sur le
mouvement de la Lune autour de la Terre (1833)
|
Effectivement, comme nous le rappelle Poisson, Clairaut maîtrisait bien le système (différentiel) exact du problème des trois corps. Mais il avait assez vite renoncé à en obtenir des formules explicites de solution -on sait depuis Poincaré qu'une telle recherche serait illusoire. Après avoir posé explicitement les six équations différentielles, Clairaut dit:
| "Intègre maintenant qui
pourra.[...] J'ai
trouvé les six équations que je viens de donner
dès les premiers tems que j'ai envisagé le
problême
des trois corps, mais je n'ai jamais fait que peu d'efforts pour les
résoudre, parce qu'elles m'ont toujours paru peu traitables.
Peut-être promettront-elles plus à d'autres. Pour
moi, je
les ai promptement abandonnées pour employer la
méthode
d'approximation ."
Alexis Clairaut,
Sur le mouvement
de la Lune autour de la Terre (1833)
|
Les Comètes
Clairaut applique sa méthode de perturbation à la trajectoire des comètes, et notamment celle qui va devenir la plus célèbre d'entres elles, la comète de Halley.| La "Comète de 1531, 1607", etc... du titre n'est autre que la célébrissime comète de Halley, ici photographiée par la NASA lors de son dernier passage, en 1986. (Source: Wikipedia Commons) | |
Les comètes "de 1531,1607,1682" étaient soupçonnées d'être un seul et même objet, réapparaissant avec une période de 76 ans: on l'attendait donc pour 1758. Mais, l'orbite étant une ellipse très allongée (ce qui explique que les retours soient très espacés), Clairaut pense qu'elle doit subir les perturbations des planètes massives connues, Jupiter et Saturne, et recalcule la trajectoire d'une façon semblable à son travail sur la lune. Il se fait aider du jeune Jérôme Lalande, et prédit un retour retardé par les perturbations, pour Mars 1759. Elle arrive en Avril, c'est un triomphe pour les deux hommes... et la théorie de Newton.
| Halley et sa comète, commémorés sur le mur de Westminster Abbey (Londres) | Portrait de Lalande, à l'Observatoire de Paris |
Pédagogue
Clairaut n'avait pas spécialement vocation à enseigner, mais il s'est trouvé d'écrire deux livres d'apprentissage, qui ont connu un large succès (il suffit de remarquer qu'ils ont été réédités de nombreuses fois, traduits dans plusieurs langues, notamment Italien et Allemand)| Toutes les pages en photos sur le site e-rara (ETH Zürich) | |
Le premier mérite une attention toute particulière: publié en 1753, il a été conçu entre 1734 et 1736, à partir des cours d'initiation qu'il donna à la marquise Émilie du Châtelet. Aussi avide de connaissances que... des hommes qui pouvaient les lui apporter -et qui étaient fort bien choisis!- elle avait quelque peu lassé Maupertuis en le pressant de passer aux... travaux pratiques; et celui-ci n'avait pu faire lever le siège qu'en la confiant à Clairaut. Si l'on en croit un Diderot quelque peu persifleur (mais peut-être voulait-il railler le rival de son ami d'Alembert dans la théorie lunaire...), cela ne lui aurait pas déplu:
|
"Il
aimait éperdument le plaisir et les femmes, et il avait vu ce
règne brillant de la Géométrie
où les
femmes titrées voulaient un géomètre
à leur
suite."
Denis
Diderot
|
La matière en est élémentaire, mais laissez l'académicien Etienne Ghys vous convaincre, en fin connaisseur, que "c'est une petit merveille" qui en remontrerait à bien des manuels (et des programmes scolaires!) d'aujourd'hui dans sa manière de démontrer -serait-ce au prix d'un escamotage provisoire (pour ne pas perturber le lecteur) sur lequel on revient plus tard, dans sa façon d'aborder les problèmes, de susciter le questionnement... Faut-il le préciser, cette présentation est à la portée de non spécialistes, qui découvriront avec surprise et ravissement qu'on peut montrer le théorème de Pythagore à l'aide de jolis découpages (pratiqués par les Chinois bien antérieurement, soit dit au passage)
Tout savoir (ou presque) sur Clairaut!
à l'Occasion de son Tricentenaire
- Vidéos des Conférences à l'Académie des Sciences (14 Mai 2013)
- Archives Clairaut: Chronologie jour par jour, Œuvres, Correspondance, Éloges et Portraits... Exhaustif et captivant!
autres ressources: ses livres
- Livres de Clairaut numérisés sur Gallica (BnF)
- Livres de Clairaut en mode Image sur le site e-rara (ETH Zürich)
ouvrages complémentaires
- G. PASCOLI, Éléments de Mécanique Céleste (Masson)
- F. TISSERAND, Traité de Mécanique Céleste, tome 3: Théorie de la Lune (Gabay). Disponible en ligne sur Gallica (BnF)
Revenir
à la Home
Page du
Mathouriste