Le Problème
des Ponts de
Königsberg est mythique pour
les informaticiens et les mathématiciens, comme
acte
fondateur de la Théorie
des Graphes d'une part, eu égard
à la
personnalité de celui qui le posa et le résolut
en 1736,
Leonhard
EULER,
d'autre part. Meurtrie par la Seconde Guerre Mondiale,
passée brutalement de l'Allemagne à l'URSS -donc
rebaptisée!-
à l'issue de la Seconde Guerre Mondiale, aujourd'hui encore
exclave
Russe (justification terminologique ici)
déconnectée du reste du territoire,
la ville peut-elle offrir au visiteur mathématicien quelque
trace de sa légende et quelque émotion ?
Sans doute la reconstruction, tardive et non à l'identique (contrairement au Centre Historique de Varsovie, victime de dommages de même ampleur), engendrera-t-elle des frustrations... mais le Mathouriste n'hésitera pas une seule seconde à vous recommander ce pélerinage scientifique. Il y voit deux raisons:
- on trouve sur place quelques vestiges significatifs et, dans le musée, des documents du passé;
- on s'y fait une raison: par sa nature, un tel problème est un problème vivant (n'en va-t-il pas de même de son homologue Parisien?), et s'il est bien connu qu'en 1945, les données plus que bicentenaires furent modifiées durablement, il l'est peut-être moins que le plus récent changement a eu lieu... en 2005! Avez-vous encore raison de dire qu'il n'a pas de solution? Suspense en images!
L'Alte Pregel, visible en bas de l'île du Kneiphof, ne l'est plus en dessous de la deuxième île! (Musée de la Cathédrale)
Mais laissons Euler formuler lui-même la fameuse question:

Le début du méoire d'Euler (lire le texte intégral)


dans la traduction d'Édoaurd Lucas, Récréations Mathématiques (texte intégral à la BnF)
Euler est un mathématicien, et cela se voit tout de suite.
À trois choses:


Vues Ouest (à gauche) et Sud-Ouest (à droite) du Kneiphof
Source de l'image centrale: R. R. Kadesch, Problem Solving Across the Disciplines (Prentice Hall)
L'idée d'Euler peut se résumer ainsi: "tout ce qui entre doit ressortir!" Donc, entrer dans un sommet (A,B,C,D) par un arc (a,b,...g) implique d' en sortir par un arc différent; donc tout sommet doit avoir un nombre d'arc y aboutissant (qu'on appelle son degré) qui est pair.
Un seul sommet de degré impair ruine immédiatement tout espoir de solution! Or, c'est le cas de l'île A (Kneiphof), donc inutile de regarder ailleurs: il n'y a pas de circuit Eulérien à Königsberg!
Notez qu'il n'y a pas non plus de chemin Eulérien: si tel était le cas, tous les sommets seraient de degré pair, sauf deux: le départ et l'arrivée de la promenade.
Lucas note avec beaucoup d'à propos:
La légende évoque les promenades dominicales des bourgeois de la ville. Quant au promeneur le plus célèbre de la cité, il n'avait que douze ans lorsqu'Euler publia sa solution, et il était réputé pour effectuer invariablement le même trajet: il est donc certain qu'il ne procédait pas à l'énumération exhaustive des chemins!
Sur le plan, la suppression de deux ponts saute aux yeux, ainsi que la transformation de l'île A, jadis habitée, en un parc. Défiguration complète?
En fait, il reste un seul bâtiment dans ce parc, c'est la Cathédrale restaurée. Adossé (à l'arrière par rapport à la photo de gauche), le mausolée d'Emmanuel Kant.
Le piéton a, lui, un peu plus de posssibilités:
des
escaliers lui permettent de descendre sur l'île depuis le
pont.
Il peut donc toujours considérer a et c comme
deux entités séparées lors de sa
promenade.
Laquelle est déjà plus agréable,
notamment dans le
calme du Kneiphof.
Malgré tout, l'ambiance a radicalement changé: remontons le temps sur le Grüne Brücke (a) , avec le tramway à deux époques, et même avant l'existence de quelque tramway que ce soit, au XVIIIème siècle.
Les ponts b et d, nous l'avons déjà signalés ont été détruits pebdant la guerre. Mais le tas de ruines qu'était devenu l'île ne doit pas qu'aux combats acharnés lors de l'assaut Sovétique d'Avril 1945; les pires dégâts furent, assez étrangement, l'œuvre des bombardements de la Royal Air Force britanique en 1944, alors que le centre-ville ne semblait pas recéler d'objectif militaire essentiel. Les forts situés en périphérie, concentrant troupes, commandement et matériels furent plutôt moins touchés...
Les deux photos anciennes ci-dessous constituent un témoignage à peine croyable de la "table rase" opérée dans le Kneiphof, seuls les murs essentiels de la cathédrale ont survécu. Le plus incroyable est la date de cette deuxième image, présentée au Musée: 15 années ont passé depuis la guerre, et aucune trace de vie sur l'ïle...

Pont c, Russie post-Sovétique: la reconquête Allemande... par l'automobile de luxe?
Une coutume insolite en
2010... qui, depuis, a essaimé dans toute l'Europe!
La vue amont sur la Neuer Pregel depuis le pont a certainement perdu de son charme avec les "barres" grisâtres de HLM soviétiques de la rive Nord (C). D'où le choix stratégique d'une photo matinale. Quant à y revenir en hiver... pourquoi pas, mais il y a peu de chance de remonter le temps!
Ainsi, bien averti que des sept ponts, seul cinq subsistaient, le Mathouriste n'avait plus qu'à achever sa tournée en trouvant le pont sur l'Alte Pregel. Chance, celui-ci se trouvait à proximité de son hôtel...
quoique... sa localisation un peu trop près de l'île du Kneiphof, plutôt avant qu'après le coude de l'Alte Pregel était de nature à laisser perplexe. D'autant qu'un médaillon sur ce pont confirma son allure "trop neuve". Était-il possible qu'il y eût un sixième pont à Kaliningrad?
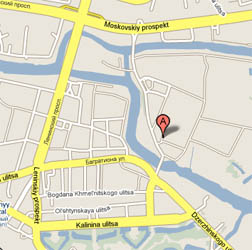
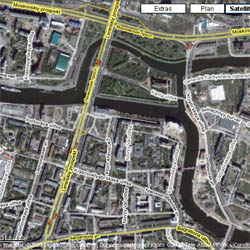
Il fallait donc réexaminer les cartes. À commencer par celle de Google: 5 ponts comme prévu... mais, ô surprise, la vue satellite en comportait effectivement un sixième! On venait donc bien de construire en 2005 cette passerelle piétonnière -large certes, mais interdite aux voitures. Nous l'appellerons donc désormais Pont h. Soyons sûr qu'Euler nous approuverait de prolonger ses notations...)
D'abord, cela ne changeait rien, du moins au problème du circuit Eulérien, le degré 3 de l'ïle A n'étant pas modifié. Tout au plus, cela ruinait-il les ambitions des amateurs d'un chemin Eulérien (un seul sommet, A, restant de degré impair).
Mais encore? Durant ce trop bref séjour -un visa d'un jour et une nuit!- pas le temps d'aller jusqu'au pont f, Hohe Brücke. Empruntons donc les images à nos sources externes!
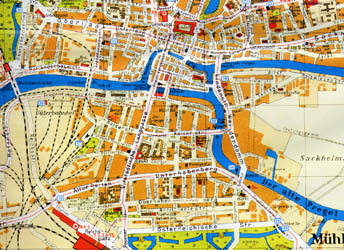
D'ailleurs, il y avait plus important. La bonne idée était d'acheter une autre carte, rééditée pour les touristes: celle de Königsberg en 1930. Elle a de plus l'avantage d'être enrichie de photos d'époques, hélas assez petites... L'image de Hohe Brücke ci-dessus en est un exemple.
Or, nouveau coup de théâtre: le pont h y figure, et il s'appelle Kaiser Brücke! Par ailleurs, il n'apparait pas sur une autre carte, datée de 1905, ce qui fournit un intervalle de 25 ans pour son édification... Bien évidemment, le Mathouriste accueillera tout encadrement plus précis avec joie!
Pour finir, on peut constater que la reconstruction s'en est faite à l'identique, ou en tout cas en respectant l'esprit du monument initial: remarquer la maison d'angle, les piles, les lampadaires...
L'augmentation du nombre de ponts avait donc eu lieu dans celle que l'on croyait immuable, la Königsberg d'avant-guerre! Königsberg a donc possédé 7, puis 8 ponts, Kaliningrad 5 puis 6. Mais à travers ces vicissitudes, le degré du Kneiphof est toujours resté impair. Et le problème du circuit Eulérien, toujours sans solution...
Et quand on rentre dîner après une journée pleine d'émotions, rien ne vaut un petit rafraîchissement. Et que voit on sur l'étiquette? Un pont sur la Pregel!

Sans doute la reconstruction, tardive et non à l'identique (contrairement au Centre Historique de Varsovie, victime de dommages de même ampleur), engendrera-t-elle des frustrations... mais le Mathouriste n'hésitera pas une seule seconde à vous recommander ce pélerinage scientifique. Il y voit deux raisons:
- on trouve sur place quelques vestiges significatifs et, dans le musée, des documents du passé;
- on s'y fait une raison: par sa nature, un tel problème est un problème vivant (n'en va-t-il pas de même de son homologue Parisien?), et s'il est bien connu qu'en 1945, les données plus que bicentenaires furent modifiées durablement, il l'est peut-être moins que le plus récent changement a eu lieu... en 2005! Avez-vous encore raison de dire qu'il n'a pas de solution? Suspense en images!
Le Problème Historique
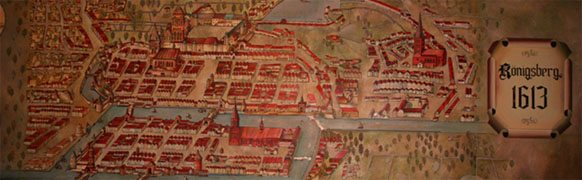
Position
Le décor est planté dès le siècle précédent, si l'on en croit cette peinture conservée au musée de la cathédrale. La rivière Pregel possède à l'Est deux bras, Alte Pregel au Sud, Neue Pregel au Nord, qui fusionnent en un seul à l'Ouest. Se trouvent ainsi définies deux îles: la plus petite, le Kneiphof, constitue le centre de la ville, fondée par les chevaliers de l'Ordre Teutonique (1255) et bien sûr on y installa la cathédrale (1327), comme on fit à Paris... l'autre est une assez longue bande de terre, encore peu urbanisée à l'époque où notre héros entre en scène.
L'Alte Pregel, visible en bas de l'île du Kneiphof, ne l'est plus en dessous de la deuxième île! (Musée de la Cathédrale)
"À Koenigsberg, en
Poméranie, il y a une île appelée Kneiphof; le fleuve qui l'entoure se
divise en deux bras, sur lesquels sont jetés les sept ponts a,
b, c, d, e, f, g.
Cela posé, peut-on arranger son parcours de telle sorte que
l'on
passe sur chaque pont, et que l'on ne puisse y passer qu'une seule
fois? Cela semble possible, disent les uns, impossible, disent les autres; cependant
personne n'a la certitude de son sentiment."
Précisons qu'il s'agit d'effectuer le parcours en revenant à son
point de départ,
ce qui n'est pas anodin: des naïfs croient parfois
s'être
montrés plus malins que lui, témoignant ainsi
d'une
solide dose d'inconscience. On nomme, en son honneur, Circuit Eulérien
un tel trajet; on pourra parler de Chemin
Eulérien si le point de départ
diffère du point d'arrivée.

Le début du méoire d'Euler (lire le texte intégral)
Ah! Un petit
problème avec vos
(éventuels) souvenirs de Latin? Pas grave, il y a une
traduction
Française dans un ouvrage assez
célèbre par
lui-même:



dans la traduction d'Édoaurd Lucas, Récréations Mathématiques (texte intégral à la BnF)
- Il formalise le problème: ne gardant du tracé que ce qui est utile, gommant tout le superflu. Il nomme Géométrie de Situation -d'après Leibniz, dit-il- cette "science [qui] s'occupe uniquement de l'ordre et de la situation, indépendamment des rapports de grandeur."
- Il généralise: ce qui est intéressant, ce n'est pas Königsberg, simple prétexte, mais la possibilité de statuer dans tous les cas qui se présenteraient; et de tracer immédiatement les figures de cas imaginaires.
- Il "algorithmise"-osons le dire. En notant ce qui fait à la fois le charme et la redoutable difficulté des problèmes combinatoires:
- Si le nombre de possibilités est faible, on peut facilement les énumérer toutes... et le problème est à la fois compréhensible et résoluble par un enfant à l'école primaire!
- S'il est important, il y faut un peu plus d'observation, et une méthode algorithmique... et c'est bien sûr ce qui l'intéresse!
Vues Ouest (à gauche) et Sud-Ouest (à droite) du Kneiphof
Solution (rapide)
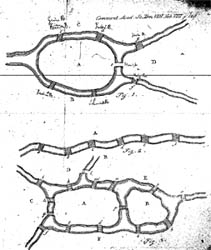
Nous adpoterons dans toute la suite les notations d'Euler pour les ponts et les rives.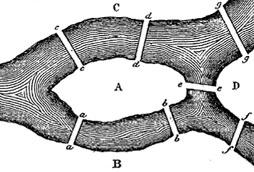 |
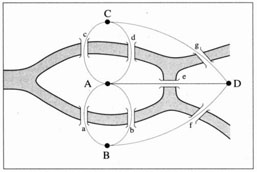 |
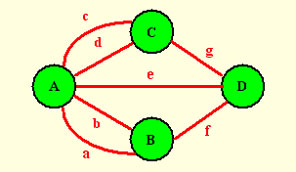 |
| Carte, dans Lucas | Poser un graphe sur la carte... | Retirer la carte: il reste le graphe! |
Source de l'image centrale: R. R. Kadesch, Problem Solving Across the Disciplines (Prentice Hall)
L'idée d'Euler peut se résumer ainsi: "tout ce qui entre doit ressortir!" Donc, entrer dans un sommet (A,B,C,D) par un arc (a,b,...g) implique d' en sortir par un arc différent; donc tout sommet doit avoir un nombre d'arc y aboutissant (qu'on appelle son degré) qui est pair.
Un seul sommet de degré impair ruine immédiatement tout espoir de solution! Or, c'est le cas de l'île A (Kneiphof), donc inutile de regarder ailleurs: il n'y a pas de circuit Eulérien à Königsberg!
Notez qu'il n'y a pas non plus de chemin Eulérien: si tel était le cas, tous les sommets seraient de degré pair, sauf deux: le départ et l'arrivée de la promenade.
Lucas note avec beaucoup d'à propos:
"J'ai observé que,
dans un grand nombre de problèmes de la
Géométrie de Situation, il y a souvent une
différence considérable dans la
manière de traiter la possibilité et
l'imposssibilité; en
général l'impossibilité se manifeste
plus facilement que la possibilité, ainsi que
l'on pourra s'en convaincre dans les théories du solitaire,
du taquin et de quelques autres jeux."
C'en est donc fini pour Königsberg... sachez tout de
même
que si cette condition issue de l'observation
élémentaire
est vérifiée, l'algorithme décrit par
Euler permet
de construire une solution, et, c'est important, dans un temps raisonnable
si l'on soumet un graphe de grande taille à un ordinateur.Grâce à Euler, vous pouvez donc répondre assez vite à la question similaire relative au graphe du métro parisien! (ne considérer que les stations de correspondance...)
Source
"Récemment, j'ai entendu parler d'un problème qui paraît se rapporter à la Géométrie de Situation..." déclare Euler dans son propos liminaire. Est-ce par son habituel correspondant, Christian Goldbach, originaire de cette ville à qui il avait offert la primeur d'un résultat du même genre sur les polyèdres? |
Euler, et son fameux théorème sur les polyèdres: La somme du nombre de faces et du nombre de sommets, diminuée du nombre du nombre d'arêtes, vaut 2. Comme le théorème des ponts de Königsberg, ce résultat est à l'interface de la topologie et de la combinatoire. Si vous êtes sceptique, vous pouvez toujours prendre un ballon de football (un vrai, en cuir, fait de panneaux polygonaux cousus) et vérifier par vous même! |
La légende évoque les promenades dominicales des bourgeois de la ville. Quant au promeneur le plus célèbre de la cité, il n'avait que douze ans lorsqu'Euler publia sa solution, et il était réputé pour effectuer invariablement le même trajet: il est donc certain qu'il ne procédait pas à l'énumération exhaustive des chemins!
Le Problème ... aux XXème et XXIème siècles!
Nomenclature Touristique
Retour à la carte, ou plutôt aux cartes, pour la correspondance des noms réels avec les notations des mathématiciens:| carte 1736 | lettre | pont | état | carte 1999 |
 |
a | Grüne Brücke |  |
|
| b | Köttel Brücke | X |
||
| c | Krauner Brücke | |||
| d | Schmiede Brücke | X | ||
| e | Honig Brücke | |||
| f | Hohe Brücke | |||
| g | Holz Brücke |
Sur le plan, la suppression de deux ponts saute aux yeux, ainsi que la transformation de l'île A, jadis habitée, en un parc. Défiguration complète?
En fait, il reste un seul bâtiment dans ce parc, c'est la Cathédrale restaurée. Adossé (à l'arrière par rapport à la photo de gauche), le mausolée d'Emmanuel Kant.
Les Ponts du Kneiphof
On a beau être prévenu, le choc à l'arrivée au centre-ville (la première vision d'un des ponts!) est quelque peu brutal: les deux ponts séparés a et c ont étés remplacés par un immense ouvrage en béton qui enjambe l'île, reliant directement, pour les voitures et les tramways, la rive B à la rive C, "survolant", si l'on peut dire, le Kneiphof. |
 |
 |
| Pont a du soir... | ...Pont a du matin! | Pont du temps jadis |
Malgré tout, l'ambiance a radicalement changé: remontons le temps sur le Grüne Brücke (a) , avec le tramway à deux époques, et même avant l'existence de quelque tramway que ce soit, au XVIIIème siècle.
 |
 |
 |
| 2009 | autour de 1900 (?) | autour de 1800 (?) |
Les ponts b et d, nous l'avons déjà signalés ont été détruits pebdant la guerre. Mais le tas de ruines qu'était devenu l'île ne doit pas qu'aux combats acharnés lors de l'assaut Sovétique d'Avril 1945; les pires dégâts furent, assez étrangement, l'œuvre des bombardements de la Royal Air Force britanique en 1944, alors que le centre-ville ne semblait pas recéler d'objectif militaire essentiel. Les forts situés en périphérie, concentrant troupes, commandement et matériels furent plutôt moins touchés...
Les deux photos anciennes ci-dessous constituent un témoignage à peine croyable de la "table rase" opérée dans le Kneiphof, seuls les murs essentiels de la cathédrale ont survécu. Le plus incroyable est la date de cette deuxième image, présentée au Musée: 15 années ont passé depuis la guerre, et aucune trace de vie sur l'ïle...
 |
 |
| Schmiede Brücke (d) aux temps de la splendeur | Restes du Köttel Brücke en...1960 ! |
Aujourd'hui,
à la place
approximative du Schmiede Brücke se trouve un petit
embarcadère, sur chacun des quais de la Pregel.
Ainsi, soir ou matin, on
peut effectuer un calme et reposant tour de l'île. Seul le
pont c
conserve une ambiance peu engageante...

Pont c, Russie post-Sovétique: la reconquête Allemande... par l'automobile de luxe?
La coupure
des arcs b
et d
a fait dire à certains qu'ils savaient résoudre
le
problème: en fait, ils se contentaient d'effectuer
l'enchaînement c-g-e-a-f,
qui est un chemin
Eulérien (deux sommets seulement de
degré impair, A
et D, mais
pas un circuit
Eulérien, toujours impossible puisque le
degré de A
est 3.
Le Honig Brücke entre les Îles
Il n'a pas changé, conservant son aspect de pont ancien. Il n'est utilisé que par les piétons qui se rendent au parc ou à la Cathédrale, et quelques véhicules de service. |
 |
| De l'île D vers l'île A | Son tablier est encore en planches! |
Une coutume locale, sans
doute
récente, veut que les jeunes fiancés ou
mariés
viennent y sceller symboliquement leur union, d'un cadenas
gravé
à leurs noms qu'ils accrochent sur le parapet
métallique,
avant de jeter la clé dans la Pregel. La même
pratique
existe un peu plus au Nord, à Klaipeda (Lituanie),
où le
bonheur est promis à ceux qui franchiront les sept
ponts de la ville! (Hasard? Symbolique usuelle du 7? Aucune allusion
explicite à un parcours Eulérien en
tous cas...)
Les Ponts de l'Île Est: une Surprise-Partie?
Le Holz Brücke (g) a lui aussi peu changé. |
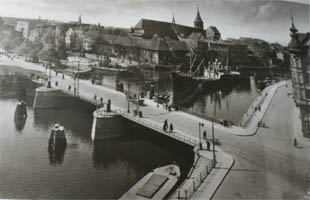 |
 |
| 2009, depuis la rive Nord (C) | Vers 1930... les bateaux venaient jusque là. | 2009, depuis l'île A (Kneiphof) |
La vue amont sur la Neuer Pregel depuis le pont a certainement perdu de son charme avec les "barres" grisâtres de HLM soviétiques de la rive Nord (C). D'où le choix stratégique d'une photo matinale. Quant à y revenir en hiver... pourquoi pas, mais il y a peu de chance de remonter le temps!
| Depuis le Holzbrücke, 1900 + ? | Du même endroit, en...été 2009! |
Ainsi, bien averti que des sept ponts, seul cinq subsistaient, le Mathouriste n'avait plus qu'à achever sa tournée en trouvant le pont sur l'Alte Pregel. Chance, celui-ci se trouvait à proximité de son hôtel...
 |

|
| Le cinquième pont: "Night and Day, you are the one..." (Cole Porter) | |
quoique... sa localisation un peu trop près de l'île du Kneiphof, plutôt avant qu'après le coude de l'Alte Pregel était de nature à laisser perplexe. D'autant qu'un médaillon sur ce pont confirma son allure "trop neuve". Était-il possible qu'il y eût un sixième pont à Kaliningrad?
Il fallait donc réexaminer les cartes. À commencer par celle de Google: 5 ponts comme prévu... mais, ô surprise, la vue satellite en comportait effectivement un sixième! On venait donc bien de construire en 2005 cette passerelle piétonnière -large certes, mais interdite aux voitures. Nous l'appellerons donc désormais Pont h. Soyons sûr qu'Euler nous approuverait de prolonger ses notations...)
D'abord, cela ne changeait rien, du moins au problème du circuit Eulérien, le degré 3 de l'ïle A n'étant pas modifié. Tout au plus, cela ruinait-il les ambitions des amateurs d'un chemin Eulérien (un seul sommet, A, restant de degré impair).
Mais encore? Durant ce trop bref séjour -un visa d'un jour et une nuit!- pas le temps d'aller jusqu'au pont f, Hohe Brücke. Empruntons donc les images à nos sources externes!
D'ailleurs, il y avait plus important. La bonne idée était d'acheter une autre carte, rééditée pour les touristes: celle de Königsberg en 1930. Elle a de plus l'avantage d'être enrichie de photos d'époques, hélas assez petites... L'image de Hohe Brücke ci-dessus en est un exemple.
Or, nouveau coup de théâtre: le pont h y figure, et il s'appelle Kaiser Brücke! Par ailleurs, il n'apparait pas sur une autre carte, datée de 1905, ce qui fournit un intervalle de 25 ans pour son édification... Bien évidemment, le Mathouriste accueillera tout encadrement plus précis avec joie!
Pour finir, on peut constater que la reconstruction s'en est faite à l'identique, ou en tout cas en respectant l'esprit du monument initial: remarquer la maison d'angle, les piles, les lampadaires...
 |
 |
| Carte postale du vieux pont | edition 2005 |
L'augmentation du nombre de ponts avait donc eu lieu dans celle que l'on croyait immuable, la Königsberg d'avant-guerre! Königsberg a donc possédé 7, puis 8 ponts, Kaliningrad 5 puis 6. Mais à travers ces vicissitudes, le degré du Kneiphof est toujours resté impair. Et le problème du circuit Eulérien, toujours sans solution...
Épilogue
Le Mathouriste espère vous avoir convaincu que la Pregel est belle et mérite une visite! Au fait, savez vous que les chercheurs de Google ont baptisé Pregel, en hommage à Euler, bien évidemment, un nouvel outil de travail sur les graphes de très grandes tailles qui modélisent le Web? (lire ce blog de Google)| Ambiances matinales sur la Pregel; les deux faces du Honig Brücke (dit encore Dom Brücke) | |
Et quand on rentre dîner après une journée pleine d'émotions, rien ne vaut un petit rafraîchissement. Et que voit on sur l'étiquette? Un pont sur la Pregel!

Consommez avec
modération! En effet, voir
les ponts en double rendra avec certitude tous les degrés
des sommets pairs...
une halucination extrêmement dangereuse, puisqu'elle
persuaderait
sa victime qu'un problème insoluble a désormais
une
solution évidente!
| Plus sérieusement, soyez attentifs: rien ne ressemble plus à un problème informatiquement facile (ie, qu'un ordinateur traitera en quelques minutes) qu'un problème informatiquement diffcile (ie, que la même machine ne pourra traiter qu'en un temps déraisonnable, très supérieur à une vie humaine... et souvent proche de celle de l'Univers!) Ainsi, si au lieu d'imposer le passage une fois une seule par les arcs (circuit Eulérien), on demande le passage une fois une seule par les sommets, (circuit Hamiltonien, nommé d'après William R. Hamilton, qui l'introduisit en 1859), le problème devient redoutable! |
Références
Touristiques
Les photos du Mathouriste ont été complétées pour comparaison par des vues anciennes issues de:- la carte 1930 de Königsberg mentionnée ci-dessus (ce sont celles qui portent un numéro de référence à la carte, en rouge);
- la remarquable carte interactive de ce site qui compare des vues de la ville avant et après 1945.
Mathématiques
Outre les textes originaux, dont les liens ont étés donnés en début de page, on pourra lire:- B. RITTAUD, Tous les Chemins mènent à Königsberg in Tangente, Hors-Série n°12: les Graphes.
- O. COGIS, C. ROBERT, Au delà des Ponts de Königsberg: Théorie des Graphes (Vuibert)
- J. HARRIS, J. HIRST, M. MOSSINGHOFF, Combinatorics and graph theory (Springer-Verlag)
- The Bridges of Königsberg in Famous Problem Page (Math Forum)
- I; PETERSON's MathTrek: Euler Bridges (MAA, 2006)
- J. HEINE BARNETT, Early Writings on Graph Theory: Euler Circuits and The K¨onigsberg Bridge Problem
- B. HOPKINS, J. WILSON, The Truth about Königsberg (College Mathematics Journal, vol.35, n°3, 2004 )