Ce que les nouveaux matériaux permettent, c'est l'augmentation
des portées: la charpente métallique permet au Goum ce que la basilique
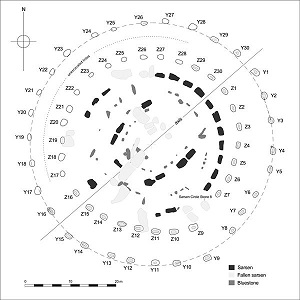
Saint Sernin ne peut offrir. De tels succès sont dans l'air du temps de
cette fin du XIXème siècle; en France, la
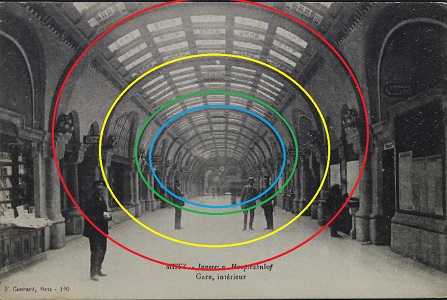
Gare d'Orsay
(1898) -devenue aujourd'hui Musée d'Orsay, après avoir passé bien près
de démolition- présente un autre bel exemple de voûte en cylindre de
révolution.

| 
|
la voûte cylindrique, au premier plan un célèbre Rodin...
| ... ou un célèbre Carpeaux!
|
En Cylindre Elliptique :
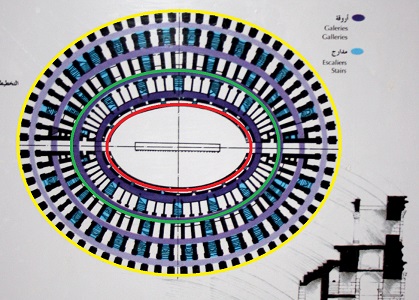
Les
voûtes
du métro parisien sont considérées comme elliptiques, quoiqu'une
construction approchée par réunion d'arcs de cercles tangents ne soit
pas exclue: si cela peut être si précis que cela prête à discussion
pour un amphithéâtre, a fortiori cela passera inaperçu sur une taille,
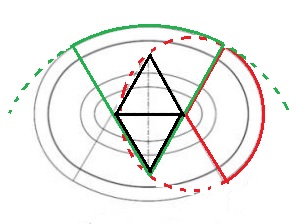
en ordre de grandeur, dix fois moins importante! Et puis, il y a la fameuse expérience acoustique de pouvoir se parler confidentiellement à voix basse d'un quai à l'autre,
les deux protogonistes se situant bien face à face, donc dans le
plan d'une unique ellipse section droite du cylindre: il suffit que les
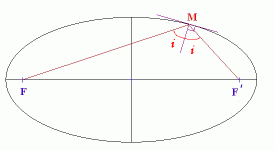
deux personnages se placent aux foyers de cette ellipse, car
- les lois de la réflexion
- dans le plan d'incidence,
- avec des angles égaux par rapport à la normale à la voûte,
- et une importante propriété géométrique de l'ellipse -jadis enseignée en Terminale: la normale bissecte les rayons joignant un point à chacun des foyers,
assureront le résultat.
En outre le secret sera garanti, car aucune
personne située en avant ou en arrière du foyer "récepteur", ni à côté
d'un de nos bavards murmurants (il n'est pas dans le plan de l'échange)
ne pourra intercepter la conversation. Stéganographie géométrique! ... et connue bien longtemps avant l'invention du métro.
|
| 
|
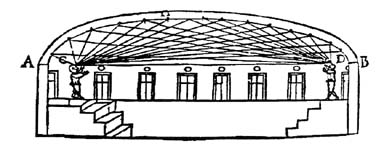
Propriété
bifocale de l'ellipse: figure "classique" et selon Athanasius Kircher,
Musurgia Universalis sive Ars Magna Consoni et Dissoni (Rome, 1650)
|
Pas si facile de réaliser
l'expérience, sauf à des heures très creuses... et bien entendu, une
bonne approximation par arcs de cercle donnera d'aussi bons résultats:
ce n'est donc pas une preuve absolue! Tant qu'à faire, nous vous
suggérons d'observer la forme (voire de tenter votre chance...) à une
station dont la voûte est particulièrement belle à regarder: parmi
toutes les signatures d'érudits qui y sont reproduites, figure celle
de'un très grand mathématicien:
Henri Poincaré!

| 
|
à la station Cluny-Sorbonne.
L'ouverture du tunnel, au fond, est, plutôt qu'une ellipse, une anse de panier, autre courbe décrivant un ovale par réunion d'arcs de cercles, mais sans chercher à simuler une ellipse.
| La signature de Poincaré est tout en haut de l'image,
ornée par la grande boucle.
|
N.B. : Attention, la célèbre
salle de l'écho de l'abbaye de la Chaise-Dieu n'est pas formé d'un, mais de deux cylindres elliptiques qui se coupent, et la fameuse propriété utilisée sur
deux ellipses diagonales seulement, contre toutes les ellipses sections droites ici (une infinité). Suivez le lien vers
notre page!
L'architecture baroque raffole des ovales en général, des ellipses en
particulier. Ce qui guide tout naturellement nos pas vers Prague, où le
monastère de Strahov offre deux superbes exemples dans ses riches bibliothèques (1670-1679):
Plus près de notre époque,
l'incroyable
gare de Metz offre un exemple de style
néo-Roman Rhénan... On
préfère, pour en juger, une vieille carte postale de l'époque où Metz
était allemande (et tout dans le bâtiment l'affirme avec force) à un
cliché d'aujourd'hui: en encombrant la partie centrale du hall de
publicités, distributeurs automatiques, on casse la vue d'ensemble,
marque d'un mauvais goût effarant (une adaptation respectueuse à la
modernité aurait été évidemment possible...) . On peut toujours hésiter
pour la section droite entre ellipse et anse de panier, mais en tout
cas la tentative de superposition d'ellipses est plutôt probante!
En Cylindre Parabolique :
La nef
des églises des Cyclades, les voûtes des
ghorfas (cellules servant de greniers à provisions) des
ksour tunisiens peut avoir une
allure parabolique (ou s'agit-il
d'un
cercle prolongé par deux tangentes? On peut parfois
hésiter! -peut-être selon l'habileté
des
bâtisseurs...).

|

| 
|
île de Santorin (Grèce)
| Ksar Ez-Zahra, région de Tataouine (Tunisie)
|

|
Il est assez probable que la forme
ait été obtenue empiriquement par les bâtisseurs, qui auront ensuite
transmis ce savoir-faire de génération en génération. Qui a constaté le
premier qu'une telle forme offrait plus de solidité qu'une section
circulaire, et partant permettait de réaliser un ouvrage plus large? Il
est à parier que cette découverte n'en fut pas une... mais plusieurs,
indépendantes dans le temps et l'espace. La trace la plus ancienne
connue se trouve en Perse antique (Iran, actuellement); il s'agit
des sépultures royales élamites de Haft-Tepe,
estimées de la fin du troisième millénaire avant notre ère!
Comparant aux célèbres tombes de Mycène (Grèce), datées environ de 1500
av. J.C. qui ne présentent qu'un piètre encorbellement, le
Mathouriste ne peut s'empêcher de repenser, mi-amusé, mi-scandalisé, à ses cours d'Histoire de 6ème, où les ennemis de la Grèce étaient présentés comme les Barbares... ces barbares étaient donc plus avancés technologiquement!
Toujours en Iran, le site sacré (zoroastrien) et fortifié de Takht-e-Suleiman (Trône de Salomon),
qui date de l'empire sassanide, offre des exemples du même ordre de
grandeur. Les matériaux varient: pierres, briques. Comme il s'agit
souvent d'espaces "techniques" (couloirs de coirculation de la
forteresse), on pardonnera une finition... disons, parfois sommaire!
|
Haft-Tepe (source inconnue)
apparence restaurée actuelle sur Wikipedia
|

| 
|

|

|
forteresse sacrée de Takht-e-Suleiman (Azerbaïdjan iranien)
|
Mais en reprenant ce principe, l'empire sassanide a fait preuve d'une grande hardiesse, édifiant ce qui restera
la plus grande arche en briques au monde: 26m d'empattement pour 37m de haut. Une arche, à elle seule symbole du rêve de l'Orient... au point d'avoir fait la publicité pour un train de rêve!

|
Le
Mathouriste avait
eu la bonne idée d'un voyage en Irak... et la mauvaise de ne pas passer
à l'acte assez rapidement! De toutes façons, il n'aurait pas pu
réaliser un cliché aérien, et celui-ci (1929) a le charme des photos
jaunies...
Qui exactement commanda la construction du palais dont elle constitue l'iwan? Shapour 1er (règne: 240-272) , après avoir écrasé l'empereur romain Valérien, ou Khosro 1er (règne:531-579) , après avoir vaincu les Byzantins en 540? Le nom actuel, Tak-Karsa,
fait pencher pour la deuxième hypothèse, mais il pourrait aussi bien,
pour marquer le "deuxième âge d'or de l'Empire Sassanide", avoir (très
substantiellement) embelli un palais antérieur. Laissons ce débat aux
archéologues, et intéressons nous à la géométrie de ce qu'on connaît
mieux sous le nom d'arche de Ctésiphon.
|
Cette arche est souvent, dans les ouvrages, qualifiée de parabolique.
Mais on a de plus en plus tendance à considérer qu'il s'agit d'une
chaînette inversée. En faveur de cet argument, le principe que Robert
Hooke (1635-1703) fut le premier à présenter par écrit en 1675, mais dont l'intuition a pu frapper les architectes dès l'antiquité :
Ut pendit continuum flexile, sic
stabit contiguum rigidum inversum."
que l'on pourrait
traduire approximativement par
"De
la même façon que pend un fil flexible,
s'élève l'arche rigide, mais de
manière
inversée." |
La parabole étant une approximation de la chaînette aux termes du
quatrième degré près, faire la distinction avec certitude n'est pas
toujours facile; on retrouve entre terrain et modèles théorique un
problème similaire à celui de la forme des amphithéâtres!
Sur la chaînette (et les cylindres associés), nous vous renvoyons à notre page dédiée, dont la vedette est la Gateway Arch de Saint Louis, Missouri.(USA); le modèle ci-contre est un exemple pédagogique qui y est présenté.
|

|

| 
|
L'arche sassanide va avoir une grande postérité, y compris dans l'architecture contemporaine., La façade du Musée National d'Iran (Téhéran) rend hommage à l' iwan de Ctésiphon, sous le trait inspiré du français André Godard
(1937). C'est plus que jamais un symbole puissant de la perennité de la
civilisation dans ce pays,où l'Islam a intégré cet élément antérieur
dans ses mosquées et médersas.
|
Musée National (Téhéran) : façade et détail de la voûte d'un iwan
|
Plus près de nous, la tour
Aazaadi, édifiée en 1971 "pour les 2500 ans de l'Empire Perse" rend un
double hommage à la voûte de Ctésiphon et à l'architecture islamique ultérieure. Appréciée de la population, elle n'a pas été vraiement menacée lors de la
Révolution de 1979; tout au plus a-t-elle changé de nom: sa première appellation
Shahyad ("Tour des Rois") évoquait trop le souverain chassé
.
Le mieux, à ce sujet, est d'écouter son toujours jeune architecte
Hossein Amanat -il gagna le concours pour ce monument alors qu'il
n'avait que 24 ans! - dans
cette vidéo (sous-titrée en Anglais) présentée sur le site de
son cabinet d'architecte. Quelques extraits, sous forme de captures d'écran:
L'arche "parabolique" de Ctésiphon a eu bien d'autres influences,
en particulier en Europe.Voici le fichier personnel de la collection de photographies d'un des plus
célèbres architecte au monde... et qu'y voit-on ,
côte à côte?
Avec les indices:
Bauhaus, Dessau, vous aurez sûrement deviné que l'architecte n'est autre que
Walter Gropius.
Plus étonnant est le bâtiment de l'image de droite: c'est l'un des deux
hangars à dirigeables édifiés à Orly (alors aéroport militaire de la
Marine Nationale) en 1921 par un grand inégénieur français,
Eugène Freyssinet (1879-1962), mondialement connu comme l'inventeur (dès 1908) du
béton précontraint, technique (
bien expliquée ici, sur le site de l'
Association Eugène Freyssinet, qui maintient le souvenir de l'homme et de l'œuvre) qui s'est largement répandue après la Seconde Guerre Mondiale.
Le
Mathouriste est particulièrement heureux d'avoir pu... photographier la photo (!), car ces hangars ont été détruits lors d'un bombardement américain en 1944. Ce qui est particulièrement intéressant, c'est que Freyssinet revendiquait explicitement la forme parabolique!
(On peut légitimement espèrer d'un X-Ponts une connaissance suffisante
de mathématiques pour ne pas confondre les deux courbes, parabole et
chaînette) Pour coffrer les nervures successives, il conçoit un cintre
en bois, léger et réutilisable, afin de le déplacer d'arche en arche.
Heureusement,
un hangar à dirigeable, un seul et unique en France, a pu
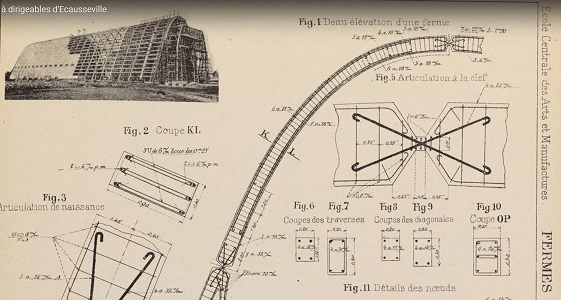
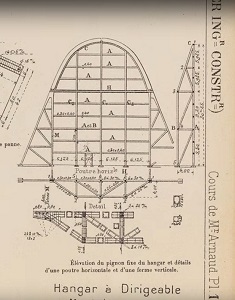
être préservé (et classé monument historique en 2003) : il se situe à Écausseville (Manche). Sa forme de
cylindre parabolique (partie supérieure seulement; elle se prolonge
ensuite vers le sol par les plans tangents) est attestée sur ce plan...
issu d'un cours à l'École Centrale!
| 
| 
|
captures d'écran issues de cette (bonne!) vidéo de présentation, qui rappelle que le bâtiment a aussi besoin de travaux de restauration!
|
Il a été conçu en 1917 par l'ingénieur
Henry Lossier (1878-1962), mesure 150m en longueur et 31m en hauteur. Mais
une fois de plus revient la question: chaînette ou parabole? Il est assez amusant de constater que
l'article qui le présente dans la revue
Le Génie Civil, en 1919, hésite plus ou moins consciemment, le texte évoquant une chaînette légèrement déformée, alors que
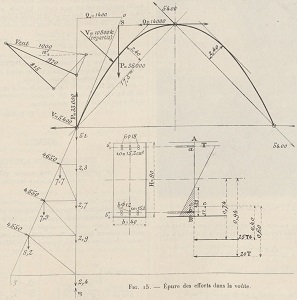
l'une des figures qui l'accompagne fait nettement pencher du côté de la parabole, grâce à une propriété classique:
le
point où la tangente est parallèle à la corde (et maximise l'écart
courbe-corde) est à une abcisse moitié de celles du sommet et de
l'extrémité!

|
|
"Les
toitures nous apparaissent communément, par la force de l'habitude,
comme devant comporter essentiellement des surfaces planes, et, facilement,
nous ne verrions dans l'emploi de formes courbes et cylindriques que le
résultat exceptionnel et imprévu d'un caprice d'artiste, la seule façon naturelle d'assurer l'écoulement de l'eau étant de la recevoir sur un plaan incliné.
Toutefois, si cette
solution semblait s'imposer, c'est avant tout parce que les charpentes
de tout temps ont été établies avec des pièces de bois ou de fer
naturellement droites [...]
À la vérité, une pente uniforme n'a pourtant rien de rationnel a priori.
La pente, en s'éloignant du faîte, devrait bien plutôt aller en
croissant, à mesure que s'accroît la quantité d'eau qu'il s'agit
d'égoutter. [...]
La voûte ayant partout une section constante, les charges permanentes sont iuniformément réparties le long de l'arc et la courbe d'équilibre théorique serait une chaînette.
M. Lossier a légèrement déformé cette courbure théorique pour tenir compte des modifications de la courbe des pressions sous les actions éventuelles du vent."
|
la consultation de ctte revue nous a été suggérée par le lien sur la page Wikipedia du hangar d'Écausseville.
| 
|