Un Tramway nommé... Banach

(souvenir de Varsovie)


C'est écrit dessus!
L'anecdote est célèbre. Laurent Schwartz ne manquait jamais de la raconter à ses étudiants, à l'École Polytechnique; il la narre lui même dans son livre de Souvenirs, Un Mathématicien aux Prises avec le Siècle :
 

Évidemment, à peine arrivé à Varsovie, le Mathouriste ne pouvait qu'envisager d'effectuer ce pélerinage mythique! L'affaire, avouons-le, avait été soigneusement préparée à l'aide du plan des lignes de la capitale Polonaise. Trois lignes: 1,14,25 se rendent à ce terminus; le plus simple est sans aucun doute de prendre le 25 du cœur même de la nouvelle ville, par exemple sur la grande avenue Marszalkowska à la station Centrum, tout proche du point de repère le plus immanquable de Varsovie, sa célébrissime Maison de la Culture, "cadeau de Staline au peuple Polonais"...
Ou à l'arrêt suivant sur  Marszalkowska, la gare centrale: Dw Centralny
Le prochain pour Banacha est dans 2 minutes! (deuxième ligne du tableau)


Mais d'abord, qu'est ce que Stefana Banacha? Pas une place, comme a réussi à nous le faire croire Laurent Schwartz... mais une avenue (d'où la féminisation par accord en genre), immensément large  -jugez plutôt- bordée d'universités.  Par contre -autre erreur (tout aussi bénigne) de notre grand mathématicien...- il y a au moins une place qui porte le nom d'un mathématicien, à savoir la place Monge, à Paris!

L'avenue Banach, par les deux bouts.

Revenons à Varsovie: à mi-avenue, un vaste espace, aussi grand qu'une place, mais qui n'a pas de dénomination particulière, accueille le terminus des trois lignes. Il est constitué d'une grande boucle de retournement, avec deux stations, une pour l'arrivée, une autre pour le départ; cette dernière a un quai unique, et les rames des différentes lignes s'y présentent à tour de rôle.

Avec un peu de patience... un représentant de chaque ligne à l'arrivée!

Il semble que le Mathouriste n'ait pas été le seul à éprouver cette surprise, si l'on en croit le Pr Krzysztof Ciesielski (Université Jagellon, Cracovie):  
"Let us finish with a not widely known story connected with Banach. There is many well known stories about Banach, as he had a very interesting personality. We shall mention here an event which happened many years after Banach's death. During the International Congress of Mathematicians in Warsaw in 1983 some mathematicians (not from Poland) discovered that one of Warsaw's streets is named after Banach. They wanted very much to see this street, so they went there. When they came to the destination they realized that there was a large area without any building. Then they commented: "This is not Banach street, but Banach space!". "

Précision:  le Mathouriste n'a découvert ce complément d'humour qu'à son retour. Comme quoi les mathématiciens ne sont jamais à court d'imagination quand tout ne se passe pas comme prévu!

Une rame de la ligne 1 vient se positionner au quai de départ.
Le tableau des départs et l'abri d'attente: les trois lignes sont indiquées en haut, à gauche; une carte de Varsovie à droite.


"Pour le principe", se dit le Mathouriste, "je vais le prendre". Vous avez déjà lu cette phrase plus haut, sous la plume de Schwartz... mais quand on a bien appris sa leçon, on passe aux applications!


et c'est le départ!
Ami(e) lecteur(tricce) arrivé(e) jusqu'ici, tu ressens le suspense à son comble, n'est-ce pas? Pourra-t-il monter, ou le tramway sera-t-il complet?

Le verdict de l'expérience est indiscutable. Impossible de décrire l'émotion de celui qui, une fois dans sa vie, aura réussi là où Schwartz a échoué.
Ah, oui, au fait, le Mathouriste, avait un truc: aller à pied à Banacha, puis... prendre le tram là-bas pour revenir au centre!

Talonné par le 25, le 1 quitte l'avenue Banacha en tournant vers le centre ville...

Un peu de sérieux...

Il y a énormément de choses à dire... et bien d'autres lieux à visiter, pour honorer la mémoire de Stefan Banach (1892-1945):
  • Cracovie, sa ville natale, où le Mathouriste   s'est enfin rendu et vous proopose sa moisson d'images, entrelacée avec de nombreux documents biographiques (suivez le lien);
  • Lwów (ou Lviv,  aujourd'hui en Ukraine) où il a fini ses jours (voir sa sépulture), mais surtout travaillé. C'est là que se situe cet autre lieu légendaire concernant Banach, le Scottish Café, au mythique recueil d'exercices. Pour vous faire patienter et vous mettre l'eau à la bouche, voici

quelques liens:

et pour savoir ce qu'est un espace de Banach:
Tentons de le dire en un raccourci. C'est un espace vectoriel dans lequel toute suite de Cauchy converge, ou, pour le dire d'une autre manière, dans lequel le critère de Cauchy est vérifié. Ce critère, Cauchy l'avait découvert pour les suites numériques (et il aurait été bien en peine de le démontrer, la notion de nombre réel n'ayant été dégagée qu'ultérieurement), en observant, dans un premier temps, que si une suite converge
    • u n+1 - u n
    •  u n+2 -  u n
    • .........
    • u n+p -  u n  pour tout p
peuvent être rendus plus petits qu'une quantité arbitraire (que l'usage fait souvent désigner par epsilon), à partir d'un rang N , qui ne dépend que de epsilon.
ça, c'est très facile... mais Cauchy avait eu l'audace de conjecturer qu'inversement, une suite ayant cette propriété converge. C'est ce qui explique le choix du mot complet, sur lequel se base le malicieux jeu de mots de Laurent Schwartz : les suites ne peuvent plus "s'échapper", à la limite, de l'ensemble considéré.
L'exemple le plus simple est celui d'une suite de fractions rationnelles convergeant vers 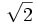: elle vérifie le critère dans l'ensemble des rationnels Q, mais n' y converge pas: Q n'est pas complet. Ce qu'affirme Cauchy, c'est que cela ne peut se produire dans l'ensemble des réels R: R est, lui, complet. L'intérêt, déjà signalé par Schwartz dans son texte, est d'affirmer que des suites convergent sans connaître à l'avance leur limite; l'extension à des espaces de fonctions (ce n'est pas pour rien que Banach est considéré comme un des fondateurs de l'Analyse Fonctionnelle) ayant cette belle propriété est énorme: c'est ainsi que les mathématiciens peuvent fièrement affirmer que, dans de bonnes conditions, les équations différentielles ont des solutions sans avoir à les calculer!

Si vous avez maintenant compris le rôle des suites de Cauchy dans la complétude des espaces, vous pourrez apprécier ce petit "lot de consolation" parisien destiné à ceux qui n'ont pas fait le déplacement en Pologne...
N'essayez pas de garer votre voiture rue Cauchy: c'est complet!

Terminons en revenant à Banach, avec une dernière image anecdotique... mais moins usuelle. C'est le fronton de cette porte de l'Université de Wroclaw (ou Breslau, dans son époque allemande) qui a attiré l'oeil et l'objectif du Mathouriste, mais... voyez le nom inscrit sur la porte! Il y a en fait une excellente raison à cet hommage: à l'issue de la Seconde Guerre Mondiale, les accords de Potsdam ont redéfini les frontières de la Pologne en la rognant à l'est, au profit de l'URSS, et en l'étendant à l'ouest au dtriment de l'Allemagne: c'est ainsi que Lwów passe en Ukraine et Wroclaw en Pologne. L'école de Lwów se réinstalle alors à Wroclaw, Steinhaus en tête.





C'est donc depuis cette université que son mentor Hugo Steinhaus (leurs deux noms sont réunis dans un fameux théorème) lui a rendu un très bel hommage (texte intégral).

La légende de leur rencontre, mais c'est sans aucun doute la réalité, veut que Steinhaus ait été attiré par la discussion de deux étudiants sur un banc, à Cracovie: Banach et Nikodym, rien de moins! Elle est encore plus réelle depuis le 14 octobre 2016, date à laquelle a été inauguré une sculpture représentant les deux étudiants sur leur banc.
Le Mathouriste, qui avait déjà une grande envie de visiter cette ville, a enfin réalisé son projet de s'y rendre et en a rapporté une moisson de souvenirs en images, à découvrir dans cette page où il vous parle de sa vie et son œuvre.

Aller à la page: Banach à Cracovie


Revenir à la Home Page du Mathouriste