Une rencontre fortuite en 1916...

	Hugo Steinhaus (1887-1972, Polonais lui aussi) est un jeune professeur qui a soutenu sa thèse sous la direction de Hilbert à Göttingen. En 1916, il vit à Cracovie et, un soir d'été, se promène, ou peut-être promène ses réflexions -les mathématiciens aiment bien réfléchir en marchant- dans le parc Planty, cette ceinture verte autour de la vieille ville qui a remplacé les fortifications après leur destruction. Ce parc apparaît en couleur pâle sur le plan urbain ci-contre (le nom est marqué en plusieurs endroits pour bien faire voir qu'il s'agit d'un seul et même espace vert), qui propose, justement, une "promenade des universités" connectant les différents bâtiments, depuis le noyau historique (ici, entouré par un tracé carré en noir). et soudain, passant près d'un banc... laissons le nous raconter l'épisode:	Hugo Steinhaus, jeune
	"Lors d'une de ces promenades, je surpris les mots "Mesure de Lebesgue". Je m'approchai du banc et me présentai aux deux jeunes apprentis-mathématiciens. Ils me dirent qu'ils avaient un troisième camarade du nom de Witold Witkosz, qu'ils appréciaient énormément. Ces deux jeunes étaient Stefan Banach et Otto Nikodym. Dès cet instant, nous nous retrouvâmes régulièrement, et... nous décidames de fonder une société mathématique." H. Steinhaus, Souvenirs (1970)

Nikodym est à gauche, Banach à droite

C'est donc une de ces discussions passionnées entre les deux jeunes gens qu'a choisi de représenter le sculpteur. La plaque informative, à côté du banc, indique qui sont les personnages, et mentionne Steinhaus; elle est rédigée en Polonais et en Anglais, mais si vous flashez le QR-code pour obtenir plus d'informations, comme on vous y invite... mieux vaut avoir préalablement étudié le Polonais! Steinhaus avait de quoi être surpris: présentée dans sa thèse en 1902, puis dans un cours édité en 1904, la nouvelle intégrale de Lebesgue était encore loin d'être répandue! timbre, réalisation personnelle: utilisable, mais non officiel! (source) édition originale, 1904 2ème édition, 1928, à lire sur Gallica Et voilà que deux jeunes autodidactes en discutaient tranquillement sur un banc...		Witold Wilkosz (1891-1941), le "troisième homme"! (article source de l'image)
	"Ma plus grande découverte en mathématiques, c'est Stefan Banach." H. Steinhaus ci-contre, Steinhaus sur son passeport en 1937 (source)

... et ses Conséquences

Immédiatement nait une collaboration qui se concrétise par un premier article en commun, publié en 1919, le premier pour Banach en temps qu'auteur. Le thème en est l'incontournable question de la convergence des séries de Fourier, pas encore formulée avec le langage des espaces vectoriels normés, que Banach n'inventera qu'une dizaine d'années plus tard. C'est d'ailleurs par souci d'éviter tout anachronisme qu'il a été décidé de graver sur l'assise du banc, non pas une expression écrite avec des normes, mais une inégalité tirée de ce premier article, réponse au défi lancé ce jour-là par Steinhaus aux deux jeunes mathématiciens. Nous vous le faisons voir ci-desssous... sans oublier  le souvenir que cela laissa à Steinhaus!
 

		La formule gravée sur le banc est une inégalité qui se trouve dans le premier texte cosigné par Banach et Steinhaus
Techniquement, de quoi s'agit-il? (Encadré à l'usage des étudiants en Mathématiques) Avec les normes et leur notation que Banach introduira plus tard, l'article rappelle d'abord le théorème de Riesz-Fischer (1907) : || f - sn ||2 tend vers 0 quand n tend vers  l'infini pour les fonctions de carré sommable (soit de l'espace L2 de Lebesgue). Puis, il pose la question: qu'en est-il pour || f - sn ||1 (soit dans l'espace L1 )? Or, en dimension infinie, il n'y  a pas d'équivalence des normes, et si ||  ||2 contrôle ||  ||1 , en vertu de l'inégalité de Cauchy-Schwarz, la réciproque n'est pas vraie, et la convergence au sens de ||  ||1 n'est liée en aucun sens à la convergence ponctuelle. La suite consiste à construire des contre-exemples, et l'inégalité gravée sur le banc sert à assurer une convergence au sens de ||  ||1 , sans que la fonction soit dans L2 , ce qui est mis en évidence par application du théorème de Parseval.   Bref, c'est une histoire d'espaces normés... avant l'heure!
" À cette époque Banach était déjà auteur d'un mémoire sur la convergence en moyenne des sommes de Fourier. C'est justement le problème que je lui avais posé en 1916 lorsque je l'avais connu dans le parc à Cracovie, problème auquel je m'intéressais sans pouvoir le résoudre. Aussi quel fut mon étonnement lorsque quelques jours après, Banach m'en donna la solution par la négative, avec pourtant une réserve vu que l'exemple de Du Bois-Reymond lui était inconnu. Une note commune de nous fut présentée à l'Académie de Cracovie par S. Zaremba avec un certain délai et ne parut qu'en 1918." H. Steinhaus, Stefan Banach, exposé à la Conférence de l'Analyse Fonctionnelle (Varsovie, 4/09/1960)

		En 1918, la Pologne retrouve une existence indépendante perdue depuis 1795 (alors partagée entre Prusse, Autriche et Russie). Dès 1919, les nouveaux amis et quelques autres collègues décident de fonder une société savante, la Société Mathématique Polonaise, qui aura son siège au 12, rue Sainte-Anne, à Cracovie, où se tenait le séminaire de mathématiques de l'Université Jagellonne. Ce bâtiment est juste en face de l'église Sainte Anne. Elle naît officiellement le 2/04/1919.
		Ci-dessus: l'église Sainte Annese reflète dans les vitres du numéro 12 Ci-contre:  document constitutif de la société. Banach et Nikodym occupent les rangs 9 et 10 respectivement; en premier est enregistré le président, Zaremba, qui avait présenté à l'Académie le premier article de Banach.

Flashback

acte de naissance (source: article de Roman Duda)		"Personne ne connaît au juste de détails sur l'enfance de Banach, mais il est notoire qu'aussitôt il fut mis en nourrice chez une blanchisseuse portant le nom de Banach qui habitait une mansarde de la rue Grodzka (au numéro 70 ou 71). À partir de ce moment Banach n'eut plus de rapport avec sa mère [...] Comme son père ne s'en occupait pas non plus, Banach dut dès l'âge de quinze ans gagner sa vie en donnant des leçons, pour la plupart des leçons de mathématiques.Il avait étudié les mathématiques en autodidacte, et lu encore au lycée le livre de Tannery sur la théorie des fonctions réelles; on ignore comment il avait appris le Français." H. Steinhaus, Stefan Banach, exposé à la Conférence de l'Analyse Fonctionnelle (Varsovie, 4/09/1960)
		Banach avec sa mère adoptive (source: article de Jaroslaw Gornicki)

Église Saint Gillles, aujourd'hui extrémité sud de la rue Grodzka, toujours très animée... ... et particulièrement un soir de Saint-Sylvestre!		En 1916, la rue finissait sous le rempart; depuis a été tracée une nouvelle rue, alors que la rue Grodzka finit à la droite de la petite église Saint-Gilles, reconnaissable à droite. Il faut imaginer la maison où vivait Banach au centre de l'image.

Le lycée "n°4" où Banach et son condisciple Wilkosz firent leurs études secondaires se trouve non loin de là, rue Podwale, donnant sur la place Na Groblach. IIl a retrouvé aujourd'hui le nom de son mécène fondateur, Bartholoùmée Nowodworski ( ca.1552-1625). Établi en 1588 -ce qui en fait un des plus anciens collège du pays- il est hébergé depuis 1898 dans ce bâtiment créé par l'architecte Józef Sare, en réhabilitant... une ancienne brasserie. Peut-être l'esprit des lieux inspira-t-il Banach... (voir la suite de ses aventures).

Après le lycée, Banach suit, fort irrégulièrement, les cours de Zaremba à l'université de Cracovie, et décide de s'inscrire à l'Université Technique de Léopol -comme dit joliment Steinhaus puisqu'en 1960 il présente son hommage en Français! Mais il s'agit à l'époque de Lemberg (Autriche-Hongrie), qui deviendra Lwów (Pologne) entre les deux guerres, puis Lvov en URSS, et enfin Lviv en Ukraine indépendante. Il revient pendant la Première Guerre Mondiale à Cracovie, mais retournera à Lwow, lieu qui va devenir décisif pour l'essor des Mathématiques Polonaises.

De la Thèse au Livre Fondateur de l'Analyse Fonctionnelle

rapport validant la thèse, signé par Steinhaus (source)

"On l'avait contraint à rédiger une thèse et à la soutenir, car il avait très vite obtenu des résultats importants; mais il persistait à dire qu'i ln'était pas prêt et que, peut-être, il allait produire des choses encore plus intéressantes. Cela finit par énerver les autorités de l'université. Quelqu'un avait recueilli en notes les remarques de Banach sur certains problèmes, et cela avait été considéré comme une excellente thèse. Mais, réglementairement, il devait y avoir une soutenance. Un jour, Banach fut abordé dans le couloir et convoqué au bureau du Doyen, sous prétexte «qu' il était venu des gens qui aimeraient connaître certains détails, et [qu'il] serait sûrement capable de répondre à leurs questions.» Banach y répondit bien volontiers, sans réaliser qu'il était examiné par une commission spéciale qui avait fait le déplacement à Lwów dans ce but." K.CIESIELSKI, On Stefan Banach  and some of his Results

Pour nos lecteurs mathématiciens...	Voyez comme tout est en place, dès les premières pages!
		L'espace vectoriel n'est pas un objet courant à l'époque de cette thèse! Tout le groupe d'axiomes [I] le définit... sans le nommer explicitement. Dans [II], on reconnaît la définition d'une norme; ainsi [I]+[II] définit un espace vectoriel normé. [III] est la propriété de complétude: toute suite de Cauchy (mais il n'emplie pas l'exppression) est convergente. [I]+[II]+[III] définit donc un espace... qui ne porte pas encore le nom de son inventeur! Suit la définition impeccable de la convergence des suites et des séries dans un e.v.n.: tout se fait au sens de la norme.
Et un peu plus loin, des résultats non moins classiques: La converence normale d'une série (si la série des normes converge, alors la série converge); le fameux Théorème du Point Fixe de Banach.
pages recomposées pour une meilleure lisibilité. La thèse complète est diponible en suivant ce lien.

En 1932, il reprend, complète et ordonne ses idées révolutionnaires: c'est la parution de son chef d'œuvre (rédigé en Français!), Théorie des Opérations linéaires. Désormais, les espaces vectoriels normés deviendront le cadre naturel de travail en Analyse Fonctionnelle des mathématiciens du monde entier, et peu à peu un chapitre incontournable de tous les enseignements, à l'université comme dans les écoles d'ingénieur. La table des matières est éloquente quant à l'évolution de l'ouvrage par rapport à sa dissertation doctorale. L'introduction présente l'intégrale de Lebesgue, puis les structures algébriques sont plus nettement dégagées: groupes au chapitre I, espaces vectoriels généraux -sic- (enfin! Que cette notion si "banale" aujourdhui fut longue à dégager...) au chapitre II. Puis arrivent les espaces normés au chapitre IV, et les espaces de type (B)  au chapitre V. Il serait douteux d'imaginer que c'est ce livre qui donna à Gainsbourg l'idée de nous présenter sa nouvelle muse comme Jane B.; toujours est-il que Banach signe sobrement son invention de sa seule initiale, avant que ne soit universellement adoptée la terminologie introduite par Fréchet en 1928: espace de Banach. La technicité va monter au fil du traité: opérateurs linéaires, convergence faible, application aux équations intégrales de Fredholm et Volterra (qui, ne l'oublions pas, avaient été à l'origine de développement des espaces de Hilbert et des e.v.n.). Le livre donne l'impression d'un ouvrage moderne, comme il commencera à s'en écrire après la Seconde Guerre Mondiale... mais on est 20 ans avant -par exemple- un classique comme: F. RIESZ & B.NAGY, Leçons d'Analyse Fonctionnelle.

Théorie des Opérations linéaires, p.55	En particulier, y apparait, sous diverses formes, le fameux résultat sur le prolongement des formes linéaires, qu'on dénomme aujourd'hui théorème de Hahn-Banach, dont l'auteur précise les articles-sources des deux protagonistes. Comme c'est souvent le cas, chacun avait travaillé de son côté sans être au courant des avancées de l'autre. Une première version avait été donnée par Helly dès 1912, dans le cas particulier d'un espace de fonctions -forcément particulier puisque, nous l'avons souligné,  c'est à Banach que l'on doit la théorie des espaces normés en général. Helly  et Riesz travaillaient alors sur le problème des moments. (source: article Wikipedia  Hahn-Banach en Anglais, bien mieux documenté historiquement)
Autre témoignage de la proximité de leurs préoccupations, Hahn avait aussi obtenu séparément un autre résultat très important en Analyse Fonctionnelle, le théorème de Banach-Steinhaus. La version princeps de celui-ci est un simple lemme (sobrement noté lemme 3) dans l'article que les deux Polonais cosignent en 1927: Sur le Principe de Condensation des Singularités. Le traité Théorie des Opérations linéaires met mieux en évidence, presque dès le début de l'ouvrage, la propriété de Baire; il donne plusieurs versions du résultat ainsi que des applications, notamment aux séries de Fourier (existence de fonctions dont la série de Fourier diverge en un point, sans les construire explicitement).

Travail intense ... au Café!

"Il pouvait causer mathématique sans moindre fatigue pendant des heures. [...]Ulam fait mention d'une séance qu'ils ont tenue à trois avec Mazur et qui dura dix-sept heures; il ajoute: «It was hard to outlast or outdrink Banach during these sessions» [...] Ces «séances» avaient le plus souvent lieu au Café Roma ou au Café Écossais. Entouré de collègues et disciples, Banach n'y rappelait en rien ce type du professeur-pédant qui craint de perdre le nimbe de sa dignité. Il a créé un nouveau mode du travail scientifique: conversations et discussions à la table d'un café, menées sans autorité professorale de la part du maître, sans crainte de blâme pour l'élève, et argumentées par les prémisses écrites au crayon sur le marbre de la table ou sur les serviettes en papier. [...]Banach ne se laissait déranger ni par les conversations aux tables voisines, ni par le va-et-vient du monde, ni même par le bruit de la musique. Beaucoup de gens doutaient qu'on puisse travailler sérieusement dans un café; cependant cette expérience de plus de dix ans a convaincu tout le monde de l'efficacité parfaite de la méthode de Banach, pratiquée dans cette ambiance spécifique. Banach a créé en quelque sorte une Bourse d'idées et de problèmes [...] H. Steinhaus,, Souvenirs de Stefan Banach (Colloquium, 1948), Nota: La citation d'Ulam est en Anglais dans le texte écrit en Français par Steinhaus.

carte postale: à gauche le Café Roma, à droite le Café Écossais (source)

carte postale: à l'intérieur du Café Écossais (source)

Lucja Banachowa (1897-1954) [source: Stefan Banach: geniusz! ]	"La liberté de conversation qu'on a au café permettait de sauter d'un problème à l'autre, de rectifier les erreurs et d'effacer sans gêne les propos conduisant à des impasses. Quant à la manière de les effacer, les garçons de café étaient d'avis fort différent. Banach ne se séparait jamais de son crayon chimique qui les mettait au désespoir, car le lavage des tables de marbre était bien embarrassant; mais il était encore plus embarrassant de faire comprendre aux autres clients ce que signifiaient ces hiéroglyphes violets." H. Steinhaus,, Souvenirs de Stefan Banach (Colloquium, 1948) "C'est pourquoi il faut signaler le mérite de madame Lucie Banach [...] d'avoir acheté un gros cahier à couverture rigide de carton et de l'avoir confié au caissier du Café Écossais. C'est là qu'on inscrivait sur les premières pages les problèmes posées en ayant soin de laisser de la place à côté des questions pour les réponses éventuelles. Ce Livre Écossais original se trouvait à la disposition de chaque mathématicien qui l'aurait demandé au café. À certains problèmes on avait attaché une prime qui variait d'une petite tasse de café à une oie vivante." H. Steinhaus, Stefan Banach, exposé à la Conférence de l'Analyse Fonctionnelle (Varsovie, 4/09/1960)
le fameux problème 153 (en V.O. dans le manuscrit et en anglais dans la dactylographie du cahier) et son prix:  une oie vivante, que Mazur remet en personne au Suédois  Per Enflo, qui en a trouvé la solution.(source de l'image)

"Ma dernière visite [en Pologne] eut lieu pendant l'été précédant le déclenchement de la Seconde Guerre Mondiale, et je me souviens, quelques jours avant que je quitte la Pologne, autour du 15 Août, d'une conversation avec Mazur, sur l'éventualité d'une guerre. L'opinion générale semblait s'attendre à une crise comme celle de Munich l'année précédente, mais ne croyait pas à l'imminence du conflit. [...] Soudain, Mazur me dit: «Une guerre peut éclater. Que devons nous faire du Livre Écossais et de nos articles non encore publiés? Tu pars bientôt pour les États Unis, où tu seras probablement en sécurité. Au cas où la ville pourrait être bombardée, je mettrai les manuscrits dans une valise que j'enterrerai.» Nous convînmes même de l'endroit de cette cachette; ce serait près des poteaux d'un terrain de football à l'extérieur de la ville. Je ne sais pas si c'est ce qui est vraiement arrivé. Apparemment, le manuscrit du Livre Écossais a survécu dans un état suffisemment bon pour qu'une copie tapuscrite puisse en être réalisée, et le Professeur Steinhaus me l'a envoyée l'an dernier." S. Ulam, préface à l'édition "Los Alamos" 1957

Revenir à Cracovie; Hommages

En 1992, pour son centenaire, la branche cracovienne de la Société Mathématique Polonaise, suggère  d'ériger une statue à sa mémoire, et propose déjà le Parc Planty comme localisation, en souvenir de la mémorable découverte de Steinhaus.  On ne sait trop pourquoi, les autorités de la ville s'y opposent, et il est finalement décidé de la placer devant l'Institut de Mathématiques. Réaliséeée par la sculptrice Margolzata  Olkuska, elle est inaugurée le 30/08/1999, pour les 80 ans de la Société Mathématique.

Le cliché ci-contre provient du site de l'artiste, en ùanteau rouge sur cette image prise lors de l'inauguration. Ceux ci-dessous sont bien sûr des photos personnelles du Mathouriste; la nuit tombe vite en Pologne, l'hiver, car l'heure officielle est celle de Paris et Berlin!

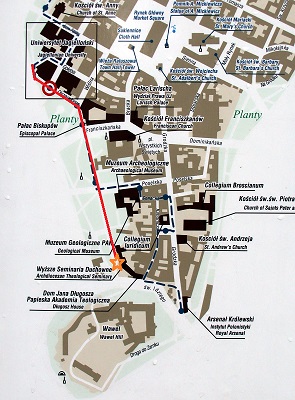L'itinéraire probable depuis le Collegium Novum, jusquà l'arrêt probable où ils s'assiéront (étoile)	Il y a beaucoup de bancs dans le parc Planty... trouver celui où ,ils discutèrent est illusoire, mais on peut déterminer presque sûrement (clin d'œil à Lebesgue) la portion la plus probable de cet espace, le quart situé entre l'ouest et le sud du parc, le Collegium Novum (lieu de la plupart des enseignements) et la fin du jardin au pied du Wavel. En effet, les trois amis avaient pour habitude de se racompagner mutuellement après les cours jusqu'au domicile de l'un d'eux. Danuta Ciesielska et Krysztof Ciesielski, membres de la commission ad hoc nommée en 2014 par le Doyen de l'Université Jagellonne, ont étudié avec soin les localisations potentielles (voir leurs articles dans le § Références). Ils pensent que si la discussion avait eu lieu en face du Collegium Novum (à la sortie des cours), Steinhaus n'aurait pas manqué de signaler cet emplacement remarquable. Pour eux, le plus vraisemblable est qu'ils aient entamé leur débat à cet endroit, poursuivi en se dirigeant vers la maison de Banach, et, n'en ayant pas terminé au moment de sortir du Parc près du Wawel -et donc de la maison de Banach- se soient assis sur un des derniers bancs afin d'achever la discussion, avant de regagner leurs domiciles respectifs.	Bancs le long des allées: il y en a partout!
	Point de départ, le Collegium Novum Point d'arrivée probable: un de ces bancs, le long du dernier bâtiment avant la sortie vers Wawel	Point  anecdotique, mais propre à nous faire sourire, Banach avait pris très jeune des habitudes sur les bancs de ce parc! (Source: article de R. Duda)

Références

Quelques articles:

• D. CIESIELSKA, K.CIESIELSKI, Stefan Banach remembered in Krakow in The Mathematical Intelligencer, vol.30 n°4 (2008)
• D. CIESIELSKA, K.CIESIELSKI, Banach in Krakow: A Case Reopened in The Mathematical Intelligencer, vol.35 n°3 (2013)
• D. CIESIELSKA, K.CIESIELSKI, Banach  and Nikodymon the Bench in Krakow Again in EMS Newsletter, June 2017
• K.CIESIELSKI, On Stefan Banach  and some of his Results in EMS Newsletter, June 2017
• R. DUDA, Facts and Myths about Stefan Banach in Banach Journal of Mathematical Analysis,  n°1 (2007)
  
• J. GORNICKI, Stefan Banach (1892 – 1945): geniusz! [en Polonais, mais très riche en iconographie, souvent inédite]
  
• H. STEINHAUS, Stefan Banach, exposé à la Conférence de l'Analyse Fonctionnelle (Varsovie, 4/09/1960).
  
• H. STEINHAUS, Souvenirs de Stefan Banach (Colloquium Math. 1, 1948),

Œuvres de Banach:

• son premier article: Sur la Convergence en Moyenne des Séries de Fourier
  
• sa thèse (1920): Sur les Opérations dans les Ensembles Abstraits et leur Application aux Équations Intégrales
  
• son mythique livre (1932):  Théorie des Opérations linéaires (disponible en ligne)
• Liste interactive de ses publications
  
• La Home Page of Stefan Banach,  où vous trouverez une foule de liens et documents! (dont les précédents)

• Une étude: F. JAËCK, Quelques Aspects de l'Élaboration de l'Analuse Fonctionnelle jusqu'à Banach (thèse, 2015)
  

Le Scottish Book et le Scottish Café:

• le manuscrit en VO. (pour l'émotion...),
  
• la transcription anglaise (pour chercher les exercices),
  
• la liste des problèmes (avec les "prix")
• le "Reprint" de Los Alamos, avec une préface de S. Ulam.
• le "Nouveau Livre Écossais" :The Lviv Scottish Book et ses problèmes qui perpétue la tradition
• le Scottish Café: article en Anglais (image du Scottish Book!), en Polonais
  
• un autre article sur Banach et le Scottish Café (K. Ciesielskii)
• Le Café Écossais sur Wikipedia (réouvert en 2014)
• Une brève vidéo (du Financial Times) tournée à Lviv (2015), avec des mathématiciens qui évoquent in situ le café et le livre.
• R.DUDA, Pearls of a lost City. The Lvov School of Marthematics (AMS) et un article de L. MALINGRANDA sur ce livre et son sujet.
  
• R.D. MAULDIN, The Scottish Book, Second Edition (Birkhaüser, 2015).
• C. ZIELINSKI. Mathematicians at the Scottish Café. IFIP International Conference on the History of Computing, Sep 2018, Poznan,
  

Quelques liens biographiques:

• La biographie Wikipedia
• La  biographie à l'Université St-Andrews
• Sur l'École mathématique de Lwów avec une belle photo de groupe.

homoré par un Doodle de Google
le 22/07/2022, 100 ans après sa nomination comme professeur

Et pour savoir ce qu'est un espace de Banach:

• pour une lecture élémentaire: la définition, parmi une biographie et les résultats essentiels de Banach;
• un résumé de cours: les résultats essentiels (niveau L2/L3)
• un article sur l'histoire de leur naissance, par Roman Duda (Université de Wroclaw)