|
Bien qu'elle ne
soit pas réglée, nous donnons ci-dessous un autre
exemple de surface ayant inspiré une œuvre de Man
Ray... et une suggestion visuelle (dont nous assumons la
responsabilité) destinée à rendre le
titre moins étranger à l'objet qu'un premier
regard pourrait laisser croire...
 |
 |
 |
Surface de Kummer
Institut
Henri
Poincaré, Paris |
Shakespearean Equation: King Lear, 1948
Hirschhorn Museum, Washington |
Shakespeare, King Lear
festival d'Avignon, années 1950-60 (?) |
Tout cela pour dire qu'après leur heure de gloire, la mise
au placard -au sens propre du terme- de ces modèles
était fort injuste. Et ce, alors même que les
ordinateurs n'avaient pas une puissance suffisante pour offrir les
représentations tri-dimensionnelles qui fleurissent partout
aujourd'hui! Bien plus en cause, un certain totalitarisme bourbachique, qui,
sévissant des années 50 aux années 80,
avait mis un point d'honneur à bannir les figures de la
géométrie. Le
Mathouriste,
qui fréquenta l'I.H.P. en 1975-76, peut
témoigner: il n'avait jamais vu ces bijoux pendant ces deux
années, et il faut rendre grâce à son
directeur actuel, Cedric
Villani, d'en avoir fait une merveilleuse mise en valeur dans
la bibliothèque.
|
|
|
Quand
le Mathouriste
était taupin, il y avait d'ailleurs une mythique "armoire
aux surfaces"
dans la salle de classe de ce qui s'appelait encore
"Spéciales A' ", menée par un grand amateur de
surfaces, Gilbert Péronny, à qui cette page est
affectueusement dédiée in mémoriam.
C'était sans doute le début de la fin, car la
clé du précieux reliquaire avait
été égarée! Reste un
témoignage du rituel:
"Ses taupins
étaient les plus férus sur les faisceaux de
coniques et de quadriques, la dualité, le tore, le conoïde de Plücker
(qui circulait dans la classe une fois
dépoussiéré) et ses
géodésiques qui se projetaient en lemniscates de
Bernoulli..."
Paul-Louis
Hennequin ,
notice-souvenir sur Gilbert
Péronny
[ En fait, ce ne sont pas les géodésiques, mais les asymptotiques: l'émotion du témoin aura sans doute causé ce lapsus technique. ]
20 ans
après (selon le titre d'un célèbre
roman), le taupin devenu prof de taupe -ah, ces
espèces qui se reproduisent... (mais rassurez-vous,
s'agissant de géométrie, elles doivent
être en voie de disparition)- pouvait en quelques lignes,
avec le logiciel MAPLE, montrer cela à ses
étudiants dans le corrigé du sujet de Centrale M 1994, ou son remake CCP TSI 2009, plus direct, plus
agréable, selon un théorème
célèbre:
"tout sujet de Centrale
présente un extremum (strict) de clarté parmi
l'ensemble des sujets voisins"
|

Gilbert
Péronny (1923-1996) |
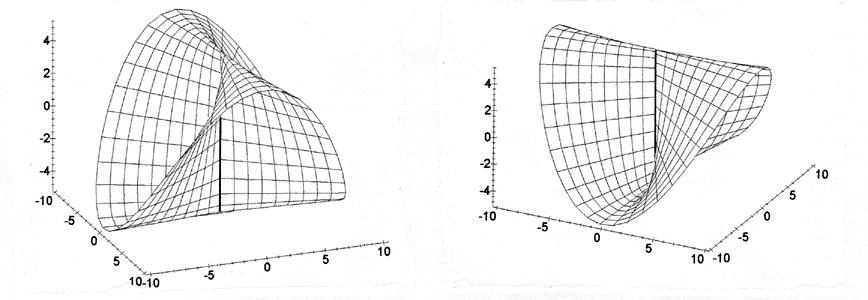
le fameux conoïde
: c'est l'ensemble des droites parallèles à un
plan fixe (ici, horizontal), s'appuyant sur une
génératrice verticale d'un cylindre de
révolution et une section elliptique de ce cylindre.
|
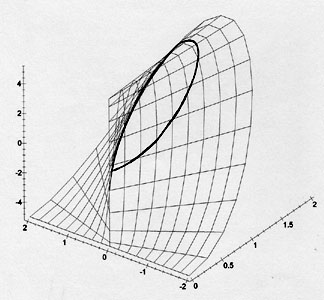 et une de ses asymptotiques! et une de ses asymptotiques! |
Mais cela
a-t-il le charme d'un modèle en fils?
Viendrait-il
à quiconque l'idée que la sculpture n'est plus de
mise, grâce à la 3D
sur écran? ...Et le plaisir de tourner autour, alors!
Nous n'avons pour l'instant pas trouvé de sculpture en
rapport à ce célèbre
conoïde... mais si ce n'est pas de l'art, Dieu que
ça lui ressemble! C'est en tout cas ce que dit ce
numéro, daté de 1961, du Courrier de
l'Unesco (intégralement disponible en ligne):
"Cette photo ne montre pas, comme
on le croirait volontiers, une sculpture abstaite. Elle
n'est autre que la projection à trois dimensions d'une
formule mathématique, dite «conoïde de
Plücker». Elle est exposée dans la salle
des Mathématiques, au Palais de la Découverte, le
grand musée parisien des Sciences."
|
 |
|
|

