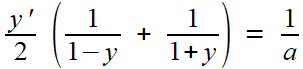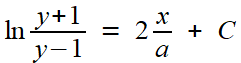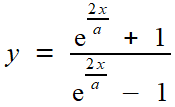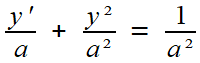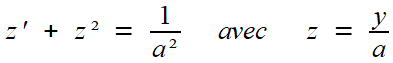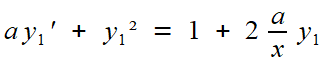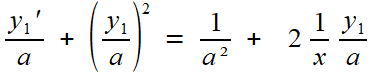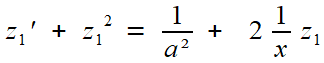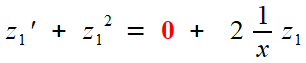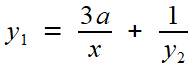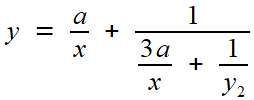e
est irrationnel... en Terminale ? Chiche!
et en version historiquement informée!
Les nouveaux programmes des lycées
incitent à utiliser davantage l'outil de l'Histoire des Mathématiques.
C'est une excellente chose, et elle sera encore meilleure -de notre
point de vue-- si elle ne se contente pas d'être "posée à côté" du
cours, mais s'accompagne de l'acte de faire des mathématiques.
Autrement dit, si donner des dates, des images, un contexte, c'est déjà
bien, et représente un progrès appréciable par rapport à un
enseignement privé de ces références, mêler histoire et exercices, c'est mieux encore.
Oser les textes sources? Pourquoi pas, mais avec discernement, car la
difficulté à les lire est très variable. Il pourra souvent être sage de
couper, il le sera toujours d'en accompagner la lecture (ou le
déchiffrement, le mot n'est parfois pas trop fort).
À la Découverte, avec Euler (1732)
On peut ad lib. sauter ce paragraphe, placé ici pour respecter la chronologie et valoriser le rôle de la découverte expérimentale en mathématiques; d'ailleurs, il ne contient aucune démonstration.
Cette preuve, la toute première,
a été donnée par Euler en 1732. Elle est à la fois très simple, parce qu'elle repose sur un
critère qui fonctionne à vue, et en même temps un peu délicate, parce qu'elle repose sur
une écriture inhabituelle d'un nombre.
Euler, à l'époque de cette découverte, est membre de l'Académie de Saint-Pétersbourg.

|

|

|
On
reconnaît, à gauche du timbre commémoratif, la tour de ce qui était à
l'époque du séjour d'Euler le bâtiment de l'Académie des Sciences; il
héberge aujourd'hui celle des Beaux Arts. Même en hiver, on peut la
voir se refléter dans le mince canal maintenu hors gel (pour
dissuader de toute traversée à pied sur la glace) au milieu de la Néva!
|
L'écriture qui dit tout!
Commençons par observer que le développement décimal
-donc usuel- d'un nombre permet de dire des choses à vue: que la
simple observation permette de ranger le nombre dans une catégorie n'a
donc rien de saugrenu.
- ou bien il est limité, et le
nombre est un décimal,
(fraction de dénominateur une puissance de 10). Ainsi, 0,415 = 415/1000.
- ou bien il est
illimité,
et le nombre n'est pas un décimal. Ainsi
de 0,333 333 ... (infiniment) = 1/3, nombre rationnel mais pas décimal,
ou encore
 ou, "plus gravement", si l'on ose dire, de e
et π .
ou, "plus gravement", si l'on ose dire, de e
et π .
Eh bien, il y a un autre développement
qui peut révéler encore plus de choses. Ce qui suit est une
simple description, mais on en apprendra plus sur le sujet en suivant
notre initiation douce aux fractions continuées.
Petite information technique: écrire un
nombre en fraction continuée
Notre nouveau
développement commence par une écriture bien usuelle, la décomposition
d'un nombre x en partie entière
(soit le plus petit entier inférieur à x), classiquement notée [x], et sa partie fractionnaire,
parfois notée (x) = x - [x], qui est donc comprise entre 0
(largement) et 1(strictement).
On peut alors écrire , avec a = [x] entier et en introduisant
la
quantité y , inverse de
x - [x]
: x - [x] = 1/y
x = a + 1/y
et par exemple e = 2
+ 0,718... = 2 + 1 / 1,392...
Ce qui est génial, c'est que, par construction, y est 0 ou un nombre plus grand que
1: on peut donc réitérer le
procédé!
y = b + 1/z
et dans notre exemple 1,392... = 1
+ 0,392.... = 2 + 1 / 2,549...
On peut empiler ...
x = a + 1/(b
+ 1/z) et par exemple e = 2 + 1 / (1 + 1 / (2 + 0,549... )
...et continuer!
x = a + 1/(b
+ 1/ (c
+ 1/u ) ) et par exemple e = 2 + 1 / (1 + 1 / (2 + 1 / 1,819... )
Le résultat est alors très simple:
- ou bien l'algorithme
s'arrête, parce qu'une division a donné le reste 0, et le nombre est rationnel;
- ou bien il se
poursuit indéfiniment, et le le nombre est irrationnel.
Pour savoir tous les détails (sans excéder le niveau Terminale, c'est ici:
|
|
On a donc là un processus d'identification à vue; le seul hic,
mais il est parfois de taille, c'est d'obtenir ce fameux développement.
Euler, qui est le premier à théoriser le sujet, va nous montrer tout le
profit qu'on peut tirer à
voir les mathématiques comme un science expérimentale!
Ce qu'Euler a découvert ...
Une fois "fabriqué" le nombre e, être ou ne pas être irrationnel devient la question, et il en est de même pour toute constante mathématique, π ou autre: elle a un statut bien déterminé, qu'il nous soit connu ou non (ainsi, on doit à Euler une autre constante célèbre, γ
, qu'on soupçonne fortement depuis d'être irrationnelle, mais dont la nature
exacte n'est toujours pas connue). Il s'agit donc bien de le découvrir!
Voici ce qu'il en dit en 1748 dans sa célèbre Introduction à l'Analyse Infinitésimale: ce n'est pas la version princeps, mais elle a l'avantage d'avoir fait l'objet d'une traduction française. Il préfère considérer (e -
1)/2, dont le développement va s'avérer un plus simple: il part d'une
valeur décimale très précise (mais inévitablement approchée) qui, en
appliquant l'algorithme rappelé, lui fait apparaître une régularité
admirable:

Bien sûr, si l'on fait le calcul
jusqu'au bout à partir de la fraction décimale, on finira par s'écarter
de cette belle progression arithmétique... puisque l'algorithme doit
se terminer pour la valeur fractionnaire retenue. Mais, en quelque
sorte, c'est trop beau pour ne pas révéler l'ordre caché de l'écriture
de e en fraction continue. Il ne la déduit pas, il l'induit.
S'il s'agissait d'une enquête policière, nous dirions que l'inspecteur
est parvenu à une intime conviction: son suspect est le bon, mais il
faut maintenant le faire avouer, c'est à dire fournir la preuve. Dans cet ouvrage, il se dérobe, se contentant d'un évasif peut se donner par le calcul infinitésimal.
Son article original , publié avec quelque retard (1737) aux Communications de l'Académie Impériale des Sciences de St Pétersbourg, est écrit ... en latin, c'est encore l'usage qui domine en ce XVIIIème siècle (encore présent au début du XIXème
siècle avec Gauss): c'est encore le langage connu de tous les savants
de l'Europe, que va peu à peu remplacer le Français, grâce à la
diffusion des Lumières... avant que l'Anglais ne le supplante comme
vecteur de communication mondiale après 1945. C'est donc un peu plus
difficile à suivre, mais les nombreuses formules qui le parsèment
jalonnent efficacement le chemin.

Dans ce texte, on le voit commencer par un développement de e,
à partir d'une valeur décimale approchée. Une régularité se
manifeste, mais de manière un peu plus compliquée que ce qu'il
retiendra pour son Introduction à l'Analyse Infinitésimale : il a donc nettoyé celle-ci de ses essais successifs au profit de l'efficacité pédagogique. Dans De Fractionibus continuis Dissertatio, il livre plusieurs développements obtenus autour du nombre e, ses racines carrées ou cubiques, son carré...
Il ne cache ni qu'il a observé des progressions arithmétiques dans les quotients partiels successifs, ni qu'il entend bien démontrer ce fait:
|
"Quant
au nombre e dont le logarithme est 1, j'en ai converti les puissances
en fractions continuées, et observé la progression aruithmétique des
dénominateurs, dont on peut considérer comme probable qu'elle se
poursuit à l'infini[...], et j'ai cherché à en démontrer la nécessité. J'ai été assez heureux d'y parvenir, grâce à une méthode particulière [...] "
L. EULER, De Fractionibus continuis Dissertatio
|
Laquelle? Nous y reviendrons plus loin, car ce n'est pas la plus facile!
La Preuve la plus élémentaire, avec
Fourier (1795)
Élève de la première promotion (1795) de l'École Normale de l'An III (future École Normale Supérieure), Joseph Fourier est rapidement remarqué comme l'un des plus brillants par ses professeurs, dont Monge, qui a été chargé de l'organisation de la toute nouvelle École
Polytechnique: c'est tout naturellement qu'il engage Fourier comme
répétiteur; et celui-ci se voit rapidement chargé de cours. Il y
restera jusqu'à son départ (1798) en Egypte avec l'expédition de Bonaparte, une nouvelle fois embauché par Monge, à qui le général a délégué le recrutement des savants.

|

|

|
Monge: sa statue à Beaune
|
Le livre de Sainville
|
Fourier, faisant cours au tableau.
(par un de ses élèves, probablement Dutertre)
|
N.B: Le dessin représentant Fourier au tableau est le premier connu qui montre un mathématicien à l'œuvre avec ses deux outils préférés: le tableau et la craie!
C'est par un obscur répétiteur,
Jeannot de Stainville, qu'on connaît la démonstration qui va suivre (le
texte de Stainville est analysé en détail sur BibNum). Stainville confesse d'ailleurs ne pas la tenir de première main, mais l'avoir reçue de Poinsot, élève de la première promotion (An IV) de l'École Polytechnique -il a donc suivi les cours de Fourier- puis professeur à l'École de 1809 à 1811.
La Démonstration d'Irrationalité
Elle repose sur l'inégalité - que nous admettrons provisoirement:
En supposant que e est une fraction rationnelle p/q, et prenant l'encadrement à l'ordre q, il vient
On chasse alors tous les dénominateurs en multipliant par q! ; à gauche figure un entier Nq tel que l'on a
ce qui place l'entier p.(q-1)! entre deux autres entiers, strictement: c'est impossible, et cette contradiction établit l'irrationnalité désirée.
Sauf que... ce n'est pas la version originale de Fourier!
Mais une version simplifiée, équivalente mais dans une présentation plus élémentaire. La vraie, votre serviteur l'a retrouvée à la Bibliothèque de l'Institut en 2021, et il est heureux de vous la présenter dans cette page.
Nous n'en dirons pas plus ici afin de respecter le cadre que nous nous
sommes fixés: aller le plus loin possible avec les moyens dun élèvede
Terminale.
Mais sachez qu'elle est beaucoup plus proche d'Euler et de ses fractions continuées, et dès lors remplace par une transition naturelle ce que l'on ressentait jusqu'ici comme une rupture méthodologique.
L'Encadrement: une Approche Naturelle, pour commencer...
Stainville s'appuie directement sur le développement en série
entière, dont il n'est pas question de parler au niveau terminale. Mais
voici un moyen aussi simple que formateur d'aller à la rencontre de ses
sommes partielles!
L'exponentielle est définie comme LA solution du problème (dit de Cauchy) : une équation différentielle avec sa condition initiale
y' = y et y (0) = 1
Abordons ce problème par analogie avec le cas des équations numériques que l'on ne sait pas résoudre explicitement: au XVème
siècle, Al-Kashi a pour traiter une équation du troisième degré inventé la méthode des approximations successives, un génial "décalage":
remplacer la question difficile x = f (x)
par le calcul facile d'un terme suivant xn+1 = f (xn)
qui donne à chaque pas un calcul très élémentaire. En espérant
que, plus on calcule de termes , plus on s'approche de la solution
recherchée... Le génie c'est de réitérer, ou, selon un des adages favoris de l'auteur de ces lignes:
"Quand c'est bon... on recommence!"
Alors pourquoi ne pas adapter l'idée? Voilà une démarche d'ingénieur:
on a un procédé qui marche bien, gardons son principe en le modifiant
pour lui faire faire un autre travail... Ici, au problème "difficile"
qu'est l'équation différentielle se substitue alors le calcul d'une
primitive, avec une valeur en 0 qui fixera la constante. y' = f est la plus triviale de toutes les équations différentielles!
Le calcul d'Al-Kashi visait sin(1°), à partir de la valeur connue de b = sin(3°) et de la formule liant le son d'un angle et ceui de son triple; la valeur numérique de b qui sera utilisée est
b = 0 .052 335 956 2 ...
équation
|
numérique
|
différentielle
|
|
3 x = 4 x3 + b
|
y' = y et y (0) = 1 |
| inconnue |
nombre |
fonction |
| approximations successives |
3 xn+1 = 4 xn3 + b
|
y'n+1 = yn et yn+1 (0) = 1 |
point de départ
|
x0 = 0 (nombre)
|
y0 (x) = 1 (fonction)
|
| 1ère approximation
|
x1 = 0, 017 44...
|
y1 (x) = 1 + x
|
| 2ème approximation |
x2 = 0, 017 452 39 ... |
y2 (x) = 1 + x + x2/2! |
| 3ème approximation
|
x3 = 0, 017 452 406 4 26 ...
|
y3 (x) = 1 + x + x2/2! + x3/3!
|
|
|
|
Dans le cas numérique, apparaissent en vert les décimales exactes: le
processus converge vite, dans ce cas. Le tracé des graphes sur [0,1]
peut fournir une undication visuelle, mais nous allons préciser
l'encadrement au § suivant.
Une récurrence immédiate fournit bien sûr
Est-ce pour autant que
- la suite converge?
- et vers une fonction solution de l'équation différentielle proposée?
Le premier point est facile à régler, très facile même pour x dans [0,1], ce qui suffit à notre affaire. La suite est croissante, et l'on a de plus
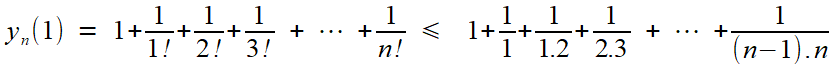
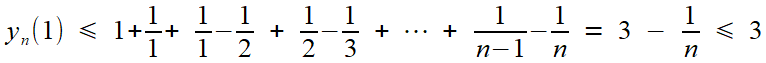
en remarquant que la fraction 1/ [ k.(k-1) ] se décompose à vue en 1/ (k-1) - 1/ k, puis en observant la compensation des termes deux à deux dans la somme. Pour les autres valeurs de pour x dans [0,1[, il suffit de remarquer
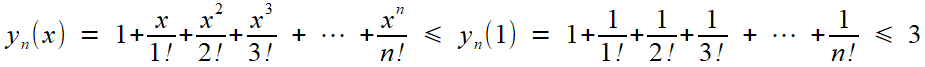
Ainsi le critère des suites monotones (Toute suite croissante et majorée converge, et vers une limite inférieure ou égale au majorant) s'applique; et pour qui ne le connaîtrait pas encore, il est très intuitif!
|
N.B. : pas beaucoup plus difficile pour x > 0 (quelconque)
Pour tout nombre b>0, on a n! > bn à partir d'un certain rang n0. Pour établir la convegence sur [0,a], on peut prendre b = a + 1 et majorer, à partir du rang n0. xn / n! par an / bn = (a / b)n ; yn (x) est alors majorée par la somme d'une progression géométrique.
|
La seconde question est bien plus délicate, elle relève de fait d'un niveau Bac+1 ou Bac+2
pour être traitée rigoureusement; c'est alors une belle contruction de
la fonction exponentielle. Même avec une "bonne qualité" de
convergence, des fonctions dérivables n'ont pas forcément une limite
dérivable; par exemple les fonctions dont le graphe est une branche
d'hyperbole 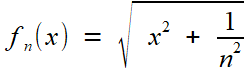 auront pour limite la fonction |x|, qui n'est pas dérivable en 0.
auront pour limite la fonction |x|, qui n'est pas dérivable en 0.
Ce travail reste donc incomplet: il faut, à ce stade, admettre que la limite démontrée est bien la fonction exp(x). Il donne néanmoins une première idée dont l'encadrement arrive.
Al-Kashi (1380-1429) est
le mathématicien qui sort du lot dans le groupe
d'astronomes qu'Ulugh Beg, "le prince des étoiles", a
réuni autour de lui à Samarcande, où il a fait construire un observatoire réputé.
Dans la medersa d'Ulugh Beg,
un groupe statuaire représente le prince entouré de son équipe de
savants; on peut imaginer qu'Al-Kashi est celui qui se tient à côté de
lui.
|

|

|
 |

|
Celui qui a repris l'idée des approximations successives pour démontrer l'existence d'une solution à une équation différentielle est Émile Picard (1856-1941).
Cette géniale adaptation (chapitre V d'nu Mémoire paru en 1890), préfigure les travaux futurs (début du XXéme siècle) de Banach et Hilbert, fondateurs de l'Analyse Fonctionnelle (opour laquelle ce sont les fonctions elles-mêmes qui sont regardées comme points d'un espace).
Picard était aussi le gendre de Charles Hermite, que nous retrouverons plus bas, aux prises avec le nombre e.
|
L'Encadrement: une Preuve Élémentaire
Supposons donc exp(x) construite autrement, comme inverse du logarithme (anciens programmes) ou limite de (1+x/n)n...
-selon les nouveaux? Elle est sa propre dérivée, donc indéfiniment
dérivable. Une succession d'intégrations par parties va nous fournir le
résultat, en partant du théorème fondamental du calcul intégral
Intégrons par parties, en considérant 1.dt = d (t - 1). Drôle d'idée, direz-vous? On serait d'abord tenté de prendre t , tout simplement, non? Eh bien, essayez, et des e1 vous resteront sur les bras à chaque tour! Il faut donc les empêcher d'apparaître lorsqu'on prend la valeur en t=1... d'où l'idée de "neutraliser" et en 1 grâce au facteur (t-1). Ou comment essayer, rater, et réfléchir pour corriger la trajectoire amène à ce que certains essaient de vous faire passer pour une astuce (Vous savez, cette fameuse formule des recueils d'exercices corrigés qui vous laissent pantois: "L'astuce est de...").
Après, c'est à vous de choisir, entre un peu de transpiration
personnelle ou l'astuce d'un autre, que vous ne trouverez bien sûr
jamais tout seul...
et voilà, mission accomplie: pas de e1 gênant. On nettoie et on prépare la réitération:
C'est nettoyé, on prépare la réitération...
Bref, avant que ça ne devienne lassant, on s'offre une petite réurrence, qui nous conduit à
une formule qui mérite d'être encadrée (les lecteurs un peu savants
reconnaissent un avatar de la formule de Taylor avec reste intégral,
mais on peut y arriver -nous l'avons fait- comme ce bon Monsieur
Jourdain; cela évite de se faire peur...
Elle prouve immédiatement l'inégalité gauche de l'encadrement, car la
fonction sous l'intégrale est (strictement) positive. Pour obtenir
celle de droite, plusieurs possibilités:
1/ On majore et par e puis par 3, 1 - t par 1. On obtient alors l'encadrement
suffisant pour prouver la convergence vers e, mais pas l'irrationalité, car l'inégalité
Nq < p. (q-1)! < Nq + 3
ne serait plus contradictoire: entre Nq et Nq + 3,
il y la place pour deux entiers. Ceci nous prouve à quel point cette
méthode de preuve -LA matrice de toute démonstration d'irrationnalité-
requiert des encadrements très serrés; le plus petit relâchement peut
être fatal.
2/ On majore encore et par e puis par 3, mais cette fois, on garde le (1 - t)n et on évalue lintégrale; on aura
puis
dont on tirera
Nq < p. (q-1)! < Nq + 3 / (q+1)
qui fournira une contradiction, sauf si q=1 ou q=2. Il faudra compléter en prouvant à part que e n'est ni entier, ni demi-entier à l'aide d'encadrements numériques. Ce n'est pas très élégant, mais cela reste probant.
2/ Pour obtenir l'encadrement utilisé par Fourier
(qu'il a obtenu , lui, selon la méthode classique de majoration
géométrique du reste d'une série, voir l'article de Stainville), il
faut raffiner un peu le traitement de l'intégrale, en écrivant
On remarque alors, par une petite étude auxiliaire, que la fonction ( 1 - t ) et varie entre 0 et 1, d'où la majoration
et notre preuve d'encadrement est enfin complète.
Euler, encore Euler!
Revenons aux fractions continuées illimitées de son premier
article; peut on en obtenir avec les moyens du programme de Terminale?
La réponse est oui... et elle
ne date pas d'aujourd'hui, puisque l'énoncé suivant (à agrandir en
cliquant) a été proposé à des élèves de Terminale!
Certes, il s'agissait d'un sujet
de... concours général, s'appuyant sur le solide programme de la
Terminale C, depuis cassée par les ministères successifs, avec cette
manie si française de démolir ce qui marche de façon performante.
Quoique'un peu crypté, (les fractions continuées se cachent sous la
récurrence double de leurs réduites, et l'origine de la fonction
auxiliaire est bien mystérieuse), il a le bon goût de commencer par une
expérience d'instabilité numérique plutôt intéressante... mais armez vous d'un stylo et de papier, la chose est raisonnablement graduée.
La fraction, parce qu'elle est infinie, grarantit l'irrationnalité de r = (3 - e) / (e - 1); mais si e était rationnel, r le serait aussi.
Euler, toujours Euler!

|

|
Carte postale commémorative: Euler et les deux bâtiments de l'Académie,
l'ancien et le nouveau ( source: site Maths Stamps de Jeff Miller)
| Le nouveau bâtiment de l'Académie Impériale:
jaune, à colonnes blanches, est construit à l'époque où Euler décède
|
Serrons maintenant de plus près son premier article, De Fractionibus continuis Dissertatio,
en jetant un regard à la "méthode particulière" employée. On
commencera par remarquer que, dans tout ce qui précède l'étude de e, Euler n'a fait que
- trouver la valeur de fractions continuées dont il se
donne la forme générale: tous les quotients partiels égaux, une
périodicité simple...
- s'occuper de nombres, alors qu'il va ici s'attaquer à des fonctions.
Les 4 pages de l'article consacrées à e
sont assez difficiles, et pas seulement parce qu'elles sont écrites en
latin!. Au bout de leur lecture, on peut au mieux être convaincu
qu'Euler a bien, par sa suite de manipulations, trouvé les fractions continues qu'il cherchait, mais pas démontré leur convergence vers les fonctions considérées.
Le recours à des équations différentielles est plutôt mystérieux: il ne
nous dit rien de ses motivations, mais on sait en étudiant ses articles
antérieurs qu'il a déjà été amené à étudier de telles équations: il ne
part certainement pas de rien! Compte tenu de la difficulté, nous nous
proposons de raconter d'abord ce qu'il fait (ou paraît faire...), puis,
nous vous laisserons admirer ces 4 pages, et pouquoi pas, forger votre
propre opinion.
Il considère l'équation différentielle (nous prenons les noms usuels x pour la variable, y= y(x) pour la fonction; Euler, on le verra, en emploie d'autres)
ay' + y² = 1
qui peut être considérée comme appartenant à deux familles
distinctes, connues des mathématiciens de l'époque, mais plus délicates
à manier que l'équation y' = y qui nous a servi de hors d'œuvre pour la méthode de Fourier:
- Les équations à variables séparables, c'est à dire celles pour qui on peut mettre "les x d'un côté, les y de l'autre"... d'où la terminologie. C'est rendu trival par le fait que x n'apparaît pas dans l'équation.
- Les équations de Riccati, du nom d'un mathématicien vénitien (1676-1754); assez incroyablement, ce nom figure dans le programme de Maths Complémentaires de Terminale, anecdotiquement certes. Car si elles ont assuré la célébrité de leur découvreur, c'est parce que, dans le cas général, on ne peut pas exprimer leur solution par une formule! Elles sont de la forme
y' = A(x) y² + B(x) y + C(x)
De la première forme, en l'écrivant
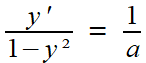 soit
soit 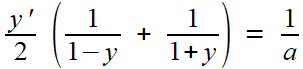
on peut tirer pour y > 1, par un calcul de primitive de chacun des côtés
soit en choisissant la constante C = 0 (de façon à ce que y devienne infini quand x s'approche de 0
La deuxième forme présente une propriété remarquable, connue d'Euler, ne serait-ce que par ses essais antérieurs: un chamgement de fonction homographique
y = (az + b) / (cz + d)
transforme une équation de Riccati en une autre équation de
Riccati;
cela va se prêter à une réitération, et la forme est idéale pour
"empiler" des fractions! De fait, plusieurs articles d'Euler -certains
sont même posthumes- lieront les développements en fraction continuée
et les équations du Comte Jacopo Riccati (Euler aime à rappeler son titre de noblesse).

|

|
Jacopo Riccati et ses Œuvres (Wikipedia)
|
Attention!
Ce qui suit est une tentative d'explication heuristique (de l'auteur de
cette page, qui en assume la responsabilité) des changements pratiqués
par Euler. Aucun document n'établit qu'il a procédé ainsi.
On va opérer comme physiciens et ingénieurs le font parfois avec un problème coriace: prendre des libertés avec la légalité mathématique,
tenter des approximations non justifiées a priori, voir ce qui se
passe... et assaisonner le tout d'un zeste de schizophrénie: rester méfiant vis à vis de sa tentative,
surtout si elle réussit! (Mais en cas d'échec, la question ne se pose
plus, on déchire et on essaie autre chose) Cela tient à la fois du ski
hors pistes et de l'espionnage en opérations spéciales qui, si elles
tournent mal, seront énérgiquement démenties par le gouvernement.
Réécoutez le début des épisodes de la série culte Mission Impossible: c'est exactement ça! Prêts pour la montée d'adrénaline?
On commence par "adimensionner" quelque peu l'équation en l'écrivant
soit encore
Maintenant, le paramètre a ne figure plus que dans un terme constant; il n'affecte plus la fonction inconnue z.
L'idée "de l'ingénieur" (les mauvaise langues diront "du chimiste",
mais il est toujours facile de railler celui qui simplifie le problème
à résoudre pendant qu'on reste les bras croisés sans idée...) est de se
dire
Cette équation est peu diffférente de z' + z² = 0 quand a est très grand.
Ce "peu différent" est l'exemple-type d'une expression mathématique qu'on n'a pas définie avec précision.
L'avantage de l'équation simplifiée, c'est qu'on en voit immédiatement une solution simple:
z = 1 / x soit y = a / x
Dès lors, ne serait-il pas naturel de poser y = a/x + u, c'est à dire, l'ajout la solution de l'équation approchée d'un terme correctif que l'on va chercher à évaluer? L'efficacité n'est pas garantie: l'idée selon laquelle "deux équations proches auront des solutions proches" est une approche intuitive, pas un théorème (C'est ce que l'on dit joliment avec le mot d'heuristique)
; Comme toutes les intuitions, elle peut se révéler trompeuse; on sait
construire des exemples où elle nous fourvoiera. Mais on ne risque rien
à essayer, ni à faire un pas de plus: nous n'errons pas dans les calculs sans but, nous visons un développement en fraction continuée. Ce qui invite à écrire
y = a / x + 1 / y1
( "Si tu ne sais pas où tu vas, tu ne risques pas d'y arriver... " Proverbe Touareg )
Le calcul qui suit est bien entendu rigoureux: c'est une simple manipulation algébrique des dérivations.
On obtient:
On ne change pas une équipe qui gagne: on reprend la même technique!
soit avec le changement de fonction z1 = y1 / a
et enfin, rien n'interdit de regarder (avec espoir) l'équation voisine
Elle reste intéressante, car, rien qu'à la regarder, on peut lui prédire une solution en K / x . En effet, la dérivée et le carré à gauche seront "en 1 / x² "; à droite, il en sera de même pour le produit de K / x par 1 / x . Donc les x² vont disparaître, et le K faisant l'affaire devra vérifier
- K + K² = 2 K soit K = 3
Comme à l'étape précédente, on se sent invité à poser
À ce stade, y est exprimée par la formule exacte (mais où y2 reste à déterminer) grâce à l'équation suivante
On poursuivra le calcul, qui devrait faire apparaître y2 = 5a / x en solution de l'équation approchée, que l'on corrigera en y2 = 5a / x + 1 / y3 . Il sera plus que temps de lancer une petite récurrence! Les quotients partiels (2n + 1)a / x apparaîtront ainsi à tous les ordres, et à tous les ordres la formule finie, exprimant y en fonction de yn, sera exacte! Ce qui n'autorise en rien à remplacer par des points de suspension...
3 petits points, cela peut sembler anodin, mais cela ne se conçoit
qu'avec une démonstration de convergence, et vers la limite obtenue par
intégration de l'équation à variables séparées. Nous avons suivi une heuristique qui a fait apparaître la forme
avec des petits calculs faciles, rien de plus, rien de moins. On peut
s'amuser (utilement) à tracer les graphes des convergents successifs -
mais un dessin n'est pas une preuve. En dépit de son souhait de rigueur
et de calculs un peu plus compliqués, Euler n'a pas fait beaucoup
mieux, et c'est Lambert qui, après avoir développé la fonction tan x avec la plus parfaite rigueur, adaptera sa méthode pour celui-ci.
Cela fournit les belles formules de son article; on peut constater qu'au début, la variable s'appelle p (x pour nous) et la fonction q (y pour nous)
Quand Hermite relit Lambert: simplifier
ou "élémentariser"?
Mais d'abord, qu'a fait Lambert (1761) ?

|

|

|
Colone Lambert à Mulhouse:
le médaillon-portrait sur la base
|
Le passage où Lambert obtient le
développement en fraction continuée de e
|
La première page
du Mémoire
|
Avec pour objectif l'irrationalité du nombre π ,
et en s'appuyant sur les liens qui unissent les fonctions
trigonométriques et l'exponentielle dans le cadre des nombres
complexes, Lambert a, en 1761:
- démontré, avec une rigueur remarquable, les développements en fraction continuée d'Euler;
- prouvé l'irrationnalité de e;
- étendu la preuve à l'irrationalité de er, pour tout nombre rationnel r;
- clairement formulé la conjecture de la transcendance de e.
Ce texte (assez long, avec des passages difficiles) est présenté en détails
sur BibNum; mais nous vous conseillons plutôt de consulter
ultérieurement cette analyse, qui serait une digression trop longue
dans le cours de la page actuelle.
Expliquons le dernier mot rencontré, transcendance de e : dire que e; est irrationnel, c'est dire qu'il n'est racine d'aucun polynôme du premier degré qx-p, à coefficents entiers. En 1840, Liouville a démontré que c'est tout aussi impossible avec un polynôme du premier degré ax² +bx+c, à coefficents a, b, c entiers (voir la preuve dans l'analyse BibNum du Mémoire de Stainville cité pour la preuve de Fourier). La transcendance, c'est généraliser à un degré n quelconque -et l'effort n'est pas mince:
Il
n'existe pas de polynôme P à coefficients entiers
relatifs tel que P(e) = 0.
et c'est cela que démontrera Hermite. [voir l'article plus bas]
Hermite, de Lambert à Padé (1872)
|
Tout ce que je puis, c'est de refaire ce qu'a déjà fait Lambert, seulement d'une autre manière [...]."
C. HERMITE, Lettre à Borchardt, Sur quelques Approximations Algébriques |

|
 |
Le texte original est encore quelques degrés de difficulté au dessus de celui de Lambert (il fait aussi l'objet d'une présentation BibNum
par Michel Waldschmidt, un des meilleurs spécialistes contemporains;
même recommandation: différer sa lecture).
Pour parvenir à son but, il
va tâcher d'approcher simultanément les diverses puissances présentes:
e, e2, e3, ..., en,
dans un hypothétique polynôme annulateur -le but étant de prouver qu'il
ne peut exister. Mais, par souci pédagogique, il présente le cas n=1,
qui conduit à une nouvelle mamière d'établir lirrationnalité, qui
repose sur une approximation de la fonction exponentielle, non plus par
des polynômes (sur quoi reposait la démonstration de Fourier),
mais par des fractions rationnelles.
|
Hermite, dessiné par Vuillier, à l'occasion du
Centenaire de l'École Normale Supérieure (1894)
|
LE fameux mémoire
(dont le titre ne laisse rien présager!)...
|
...
et ci-dessous, les deux pages où il réalise la démonstration
d'irrationnalité alternative à celle de Lambert, en une sorte de
préliminaire à sa démonstration de transcendance.
|
|
|

|

|
|
Il ne cache pas, comme on le
voit dans le dernier encadré, sa filiation spirituelle : les fractions
rationnelles qu'il manipule sont directement issues du développement en
fraction continuée de Lambert; ce sont les réduites des fractions approximatives obtenues en tronquant le développement infini à 1,2,3, ... n
"étages" du développement infini, c'est à dire la fraction réduite
(d'où le nom:!) à un seul numérateur et dénominateur d'une fraction à n étages. Sauf que la transformation intermédiaire est demeurée dans l'ombre.
La présentation ci-dessous, sous forme d'exercice gradué, n'emploie aucun outil qui excède le programme de Terminale.
Toutefois, le rythme des questions en fait plutôt un texte de niveau
Math Sup ou L1, mais rien n'empêche de l'adoucir par quelques questions
intermédiaires.
Voyant qu'il y a là un filon à exploiter, Hermite en confiera l'étude, en sujet de thèse, à un de ses élèves, Henri Padé (1863-1953): ces fractions rationnelles d'approximation portent désormais le nom d'approximants de Padé. Alors que les questions d'irrationnalité appartiennent aux mathématiques les plus pures, elles sont utilisées très efficacement dans
les calculs numériques approchées de la physique et de l'ingéniérie, où
elles se montrent souvent plus précises et plus économes (en opérations
effectuées) que les polynômes. Ainsi, l'ordinateur IBM 360
utilisait-il un approximant de Padé comme substitut, à une quantité
négligeable près (compte-tenu des décimales affichées), de... la
fonction exponentielle!
Hermite, une dernière... (1873)
|
"On reconnaîtra volontiers que, dans le domaine mathématique, la possession d'une vérité importante ne devient complète et définitive qu'autant qu'on a réussi à l'établir par plus d'une méthode."
C. HERMITE, Sur l'Irrationalité de la Base des Logarithmes Hyperboliques |
Beau sujet de philosophie mathématique, non? Car une seule suffit
bel et bien, évidemment, sur le plan logique. Mais est-ce pour autant
que la compréhension du résultat sera totale? Gauss offre un exemple
illustre de cette attitude (par exemple, ses démonstrations du théorème fondamental de l'Algèbre), qui n'est pas rappeler celle des
alpinistes: être le premier à vaincre le sommet, bien sûr, mais ouvrir
de nouvelles voies aussi...
Il est tout à fait remarquable qu'étant venu à bout de la transcendance de e, Hermite s'intéresse encore à son irrationalité.
Il "remixe" donc la preuve précédente en la débarassant des intégrales.
Il faut pour l'aborder une petite connaissance des séries entières: on
dépasse en cette fin de page, et pour la première fois, le niveau qu'on
s'était imposé. Mais c'est la fin, et voir la citation du cadre vert
dans son contexte est tout de même intéressant, non?
Bibliographie
Textes historiques (Sources Premières)
- L. EULER, les Archives EULER: tout Euler en ligne!
- C. HERMITE, OEUVRES COMPLETES
- H. LEBESGUE, Leçons
sur
les Constructions Géométriques
(Gautheirs-Villars,
réédition J. Gabay)
Ouvrages de Références (niveau **)
- H. BOUALEM, R. BROUZET, La Planète R
(Dunod)
- C. BREZINSKI, History
of Continued Fractions and Padé Approximants (Springer)
- E. HAIRER, G. WANNER, Analysis by its History (Springer)
- X. HASCHER, A. PAPADOPOULOS, Leonhad
Euler: Mathématicien, Physicien & Théoricien de la Musique (CNRS
Éditions)
- J. HAVIL, The
IrratiΦnals (Princeton University Press)
- I. NIVEN, Numbers: Rational & Irrational (The L. W Singer
Company)
- C. OLDS,
Continued
Fractions (MAA)
- M.SERFATI, Quadrature
du
Cercle, Fractions Continues et Autres Contes (Brochure
APMEP
n°85)
- J. STILLWELL, Mathematics and its History (Springer)
Ouvrages de Références (niveau ***)
- D. DUVERNEY, Théorie
des Nombres (Dunod)
- G. HARDY, E. WRIGHT, An Introduction to the Theory of Numbers (Oxford)
- ,J.H. SILVERMAN, A Friendly Introduction to Number Theory
(Pearson)
- M.WALDSCHMIDT, Nombres
Transcendants. (Springer, Lecture
Notes in Mathematics
402).
Sur
la Toile
 ou, "plus gravement", si l'on ose dire, de e
et π .
ou, "plus gravement", si l'on ose dire, de e
et π .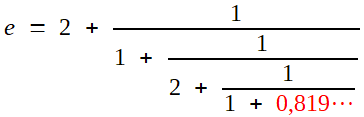



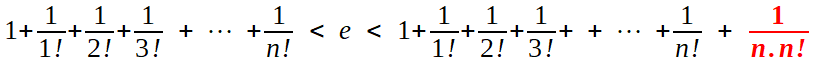
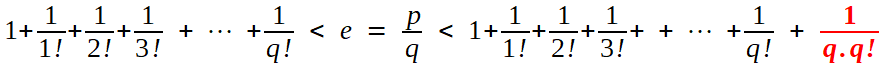
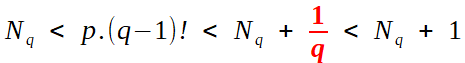
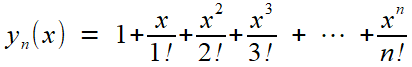
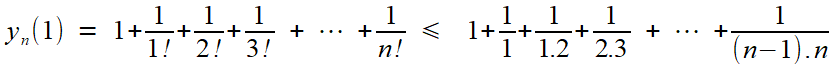
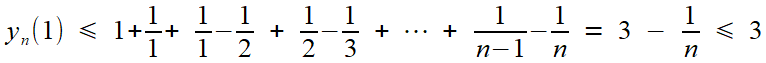
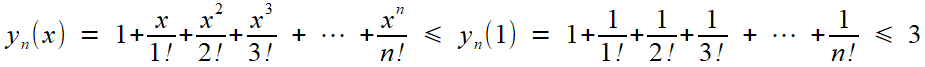
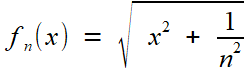 auront pour limite la fonction |x|, qui n'est pas dérivable en 0.
auront pour limite la fonction |x|, qui n'est pas dérivable en 0.




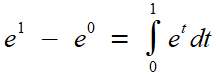
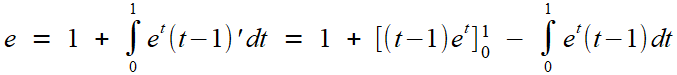
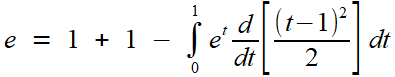
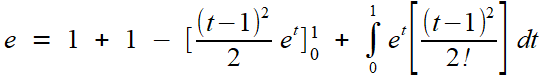
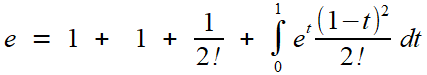
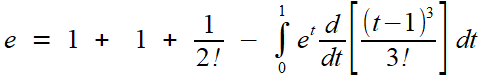
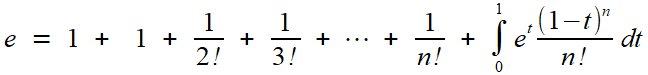
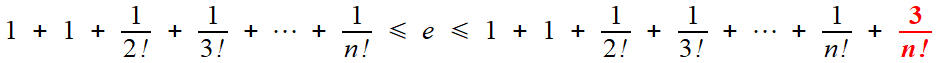
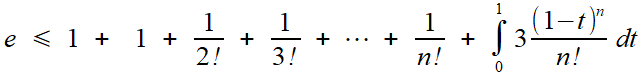
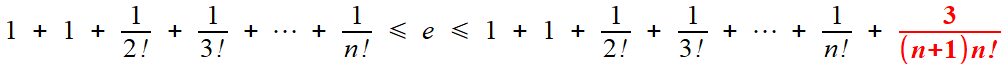
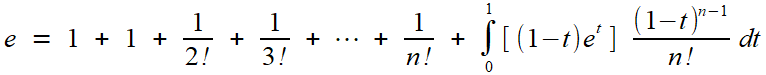
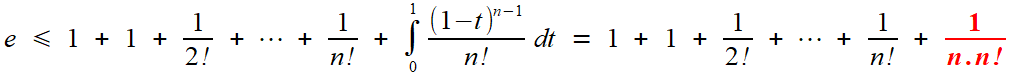
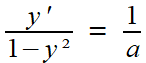 soit
soit