So Watt !
 |
Mon nom est Watt. James Watt.
"Ceux qui considèrent seulement James Watt comme un grand ingénieur mécanicien se font une une idée très erronnée de sa personnalité: il s'est également distingué comme physicien et chimiste, et ses inventions démontrent sa profonde connaissance de ces sciences, et cette caractéristique particulière de son génie, les unir dans les applications pratiques" Sir Humphrey Davy (1778-1829), 1824
|
|
|
Et ce n'est pas tout, car, comme on le verra plus bas, ses travaux lui
firent faire une incursion en géométrie... ce qui justifie sa présence
dans nos pages.
à gauche: statue de James Watt, dans sa ville natale, Greenock (Écosse) à droite: Greenock, vue de l'est. Peinture de John Fleming, vers 1810 |  |
|
Comment découvrir un Musée...
Le Mathouriste n'avait absolument pas prévu de se rendre à Greenock, dont il
ignorait jusqu'à l'existence... Mais les caprices, ou plutôt les
fureurs de Neptune ont parfois des effets bien inattendus, et ce n'est
pas un certain Ulysse qui vous dirait le contraire! Une croisière dans
les îles britanniques, en plein mois d'août, voguait vers les
Hébrides... quand une tempête et les ordres des autorités portuaires de
Stornoway (Harris & Lewis) obligèrent le capitaine à chercher un
refuge pour 48h: ce fut la large embouchure de la Clyde, abri idéal...
et le port de Greenock, jadis centre d'une activité intense.Que faire de ce temps d'ecale imprévu, sinon explorer la ville? En y découvrant, à un angle de rues, une plaque "Watt street", la première pensée du fut pour la chanson de Boris Vian, hommage à une rue parisienne insolite que lui avait fait découvrir Raymond Queneau -une rue traversant par dessous les voies de la Gare d'Austerlitz, soutenues par d'imposantes colonnes en fonte...
Si vous ne la connaissez pas, écoutez-la grâce au lien ci-dessous (si intriguante en l'absence de photos que votre serviteur lui réserva son premier pélerinage touristique dans Paris, entre deux planches d'oraux de concours!)
 |
 |  |
| rue Watt, à Greenock | écouter la chanson de Boris Vian, par P. Clay | rue Watt, à Paris (source de l'image: l'étrange rue Watt, de Paris Promeneurs) |
Mais, après tout, en Écosse, quoi de plus normal qu'une rue qui rend hommage à un grand Écossais? So what, se dit le visiteur, songeant cette fois au célèbre thème de Miles Davis... (d'où l'idée pour le titre de cette page, hé,hé...). Et ô surprise, au bout de la rue Watt, nous attend... un musée James Watt!
 |
 |  |
| une bâtisse... très britannique. | une stèle en l'honneur de l'enfant du pays |
 |
Sur
le petit côté du parallélépipède qui porte la stèle aux multiples
visages, le chef d'œuvre de l'ingénieur: sa machine à vapeur.
Saurez-vous distinguer déjà ici le parallélogramme de Watt (facile!) et le mécanisme à 3 barres de Watt (plus dur!) qui convertit une trajectoire circulaire en trajectoire droite? Enfin, presque... C'est de cela que nous allons vous reparler en détails ci-dessous! |
|
 détail de la stèle |  plaque métallique du chemin "héritage de James Watt" |
|
 |
À
l'entrée, nous sommes accueillis par un imposant régulateur à boules.
Ce type de système était déjà présent dans certains moulins à vent,
avec le même but: réguler la vitesse de manière à ce qu'elle soit
approximativement constante, mais c'est Watt qui eut l'idée de le
greffer sur la machine à vapeur, avec des résultats remarquables!
En fait, nous aurions pu observer la présence du dispositif, et in situ, sur la machine présentée dans le parc, avant d'entrer. |
|
Rappel de physique: le régulateur à boules
< à compléter>
|  |
|
Très vite, le musée nous présente les ancêtres du grand ingénieur, par des peintures dont les auteurs sont inconnus. Au texte, sobre et factuel des cartels, nous préfèrerons le lyrisme de François Arago, dans son hommage posthume devant l'Académie des Sciences (car Watt en avait été élu membre à titre étranger), d'autant qu'il commence par un rappel dont la pertinence est toujours d'actualité: bien des fois, le Mathouriste a ressenti beaucoup plus de souci mémoriel pour les hommes de science de l'autre côté du Channel!
|
"James Watt, un des huit savants étrangers de l'Académie des Sciences, naquit à Greenock, en Écosse, le 19 janvier 1736. Nos
voisins de l'autre côté de la Manche ont le bon esprit de de penser que
la généalogie d'une famille honnête et industrieuse est tout aussi
bonne à conserver que les parchemins de certaines maisons titrées, devenues seulement célèbres par l'énormité de leurs crimes ou de leur vices. Aussi puis-je vous dire avec certitude que le bisaïeul de James
Watt était un cultivateur établi dans le comté d'Aberdeen; qu'il périt
dans la bataille de Montrose; que le parti vainqueur, comme c'était
(j'allais ajouter, comme c'est encore) l'usage dans les discordes
civiles, ne trouva pas que la mort fût une expiation suffisante des
opinions pour lesquelles le pauvre fermier avait combattu; qu'il le
punit, dans la personne de son fils, en confisquant sa propriété; que
ce malheureux enfant, Thomas Watt, fut recueilli par des parents
éloignés; que dans l'isolement absolu auquel sa position difficile le
condamnait, il se livra à des études sérieuses et assidues; qu'en des temps plus tranquilles il s'installa à Greenock, où il enseigna les mathématiques et les instruments de la navigation [...] Thomas Watt eut deux fils. [...] [Le cadet, James], père du célèbre ingénieur, longtemps membre trésorier du conseil municipal de Greenock et magistrat de la ville, [...] cumulait (n'ayez point de crainte: ces trois syllabes, devenues en France une cause générale d'anathème, ne feront pas de tort à la mémoire de james Watt), il cumulait trois natures d'occupation: il était à la fois fournisseur d'appareils, d'ustensiles et d'instruments nécessaires à la navigation, entrpreneur de bâtisses et négociant [...]" F. ARAGO, Watt in Œuvres, t.1
|
 James Watt Sr (1699-1782), le père de James |
 Thomas Watt (1642-1734), le grand-père de James |
La bataille où mourut l'arrière-grand-père de Watt est aussi connue sous le nom de Brig of Dee (1639), épisode anglo-écossais de la Guerre des trois Royaumes (1639-1653).
De santé fragile, le jeune James commence son éducation à la maison, apprenant à lire avec sa mère, à écrire et compter avec son père, qui le familiarisa aussi avec l'outillage et les techniques d'atelier.
Arago fait sienne une anecdote que Watt lui-même n'a jamais mentionné, mais qui a donné lieu à de nombreuses illustrations dans son pays natal. Il est d'ailleurs amusant de voir qu'en France, nos livres d'histoire en racontaient une similaire à propos de la découverte de la puissance de la vapeur par Denis Papin!
 gravure de J. Scott d'après une peinture de M. Stone (1840-1921) Science Museum, Londres |
"James Watt, au surplus, augurait très favorablement des facultés naissantes de son fils. Des parents plus éloignés et moins perspicaces ne partageaient pas les mêmes espérances. «James, dit un jour madame Muirhead à son neveu, je n'ai jamais vu un jeune homme plus paresseux que vous. Prenez donc un livre et ooccupez vous utilement. Il s'est écoulé plus d'une heure sans que vous ayez articulé un seul mot. Savez vous ce que vous avez fait pendant ce long intervalle? Vous avez ôté, remis, et ôté encore le couvercle de la théière; vous avez placé dans le courant qui en sort , tantôt une soucoupe, tantôt une cuiller d'argent; vous vous êtes évertué à examiner, à réunir entre elles les goutelettes que la condensation de la vapeurformait à la surface de la porcelaine ou du métal poli; n'est-ce pas une honte que d'employer ainsi son temps! » [...] lorsque bientôt j'expliquerai que la principale découverte de notre confrère a consisté en un moyen particulier de transformer la vapeur en eau les reproches de madame Muirhead soffriront à notre esprit sous un tout autre jour,;et le petit James, devant la théière, sera le grand ingénieur préludant aux découvertes qui devaient l'immortaliser; et chacun trouvera sans doute que les mots: condensation de vapeur, soient venus se placer naturellement dans l'histoire de la première enfance de Watt. Au reste, je me serais fait illusion sur la singularité de l'anecdote, qu'elle n'en mériterait pas moins d'être conservée." F. ARAGO, Watt in Œuvres, t.1
|
|
En dépit de ses soucis de santé, il ne vit pas confiné, et son père veille à une éducarion équilibrée, avec sa part de grand air frais et revigorant:
|
"Sa vocation était difficile à découvrir, car le jeune étudiant s'occupait de tout avec un égal succès. Les rives du Loch Lomond, déjà si célèbres par les souvenirs de l'historien Buchanan et de l'illustre inventeur des logarithmes, développaient son goût pour les beautés de la nature et de la botannique. Des courses sur diverses montagnes d'Écosse lui faisaient sentir que la croûte inerte du globe n'est pas moins digne d'attention, et il devenait minéralogiste. James profitait aussi de ses fréquents rapports avec les pauvres habitants de ces contrées pittoresques, pour déchiffrer leurs traditions locales, leurs sauvages préjugés. Quand la mauvaise santé le tretenait sous le toit paternel, c'était principalement la chimie qui devenait l'objet de ses expériences." F. ARAGO, Watt in Œuvres, t.1
|
|
 |
 |
| Le Loch Lomond, dans une ambiance... très écossaise! |
|
C'est d'une manière très particulière qu'il entre à l'Université de Glasgow: par la petite porte, pour ne pas dire la porte de service!
|
"En 1755, il alla à Londres se placer chez M. John Morgan, constructeur d'instruments de mathématiques et de marine, dans Finch Lane, Cornhill. L'homme qui devait couvrir l'Angleterre de moteurs [...] entra dans la carrière en construisant, de ses mains, des instruments subtils, délicats, fragiles [...]. Watt ne resta guère qu'un an chez M. Morgan, et retourna à Glasgow où de graves difficultés l'attendaient. Appuyés sur leurs antiques privilèges, les corporations d'arts et métiers regardèrent le jeune artiste de Londres comme un intrus, et lui dénièrent obstinément le droit d'ouvrir le plus humble atelier. Tout moyen de conciliation ayant échoué, l'Université de Glasgow intervint, disposa en faveur du jeune Watt d'un petit local dans ses propres bâtiments, lui permit d'établir une boutique, et l'honora du titre d'ingénieur. [...] Watt atteignait à peine sa vingt et uniième année, lorsque l'Université de Glasgow se l'attacha. Il avait eu pour protecteurs Adam Smith, l'auteur du fameux ouvrage sur la Richesse des Nations; Black, que ses découvertes concernant la chaleur latente et le carbonate de chaux devaient placer dans un rang distingué parmi les premiers chimisyes du XVIIIème siècle; Robert Simson, le célèbre restaurateur des plus importants traités des anciens géomètres. Ces personnages [...] ne tardèrent pas à reconnaître l'homme d'élite, et lui vouèrent la plus vive amitié. Les élèves de l'Université tenaient aussi à l'honneur d'être admis dans l'intimité de Watt. Enfin sa boutique, oui, Messieurs, une boutique! devint une sorte d'académie où toutes les illustrations de Glasgow allaient discuter les questions les plus délicates d'art, de science et de littérature. conservée." F. ARAGO, Watt in Œuvres, t.1
|  statue d'Adam Smith à Glasgow (Écosse) |
 portrait de Robert Simson dans un de ses ourages (source: Wikimedia Commons) |
N.B: Simson fut, en effet, le premier traducteur en Anglais des Coniques d'Apollonius et des Éléments d'Euclide, remettant à l'honneur ces livres sans qu'il soit besoin de recourir aux langues anciennes, grec ou latin.
Les portraits de Watt ne semblent pas nombreux (c'est un peu surprenant, au vu de la notoriété acquise de son vivant); il a eu en tant que modèle, on le verra plus bas, bien plus de succès dans la statuaire. Le musée de Greenock possède une copie, par J. Partridge (1790-1870) d'après l'original réalisé par Sir William Beechey (1753-1839). Et un exemplaire d'un buste qu'on retrouvera aussi au Science Museum de Londres.
 |
 |  |
| petits objets souvenirs, dans une vitrine. Noter le médaillon qui reprend ce portrait |
Le génie polymathe de Watt n'est pas toujours perçu, tant ses travaux sur la machine à vapeur et leur succès éclatant dans l'avènement de la Révolution Industrielle jetèrent dans l'ombre d'autres inventions. Le musée de Greenock a la bonne idée de nous présenter un de ses réussites de l'époque: on lui doit l'ancêtre de la photocopieuse! Enfin, une machine copieuse, sans photo évidemment, puisque son principe de fonctionnement était chimique: une encre spéciale pour l'original, un papier spécial pour la copie, obtenue par pressage (un lourd cylindre de métal roulant sur les deucx feuilles). Nous avons choisi de le mettre en regard d'un souvenir du physicien John Robison (1739-1805), encore étudiant à l'Université de Glasgow, qui devait devenir secrétaire de la Royal Society d'Édimbourg et contributeur notoire de l'Encyclopædia Britannica (un projet né à Édimbourg en 1771, en "réaction conservatrice" à la révolutionnaire Encyclopédie de Diderot et d'Alembert)
 |
 |
"Quoiqu'élève encore, j'avais la vanité de me croire assez avancé dans mes études favorites de mécanique et de physique, lorsqu'on me présenta à Watt; aussi, je ne fus pas médiocrement mortifié en voyant à quel point le jeune ouvrier m'était supérieur... Dès que, dans l'Université, une difficulté nous arrêtait, et quelle qu'en fût la nature, nous courions chez notre artiste. Une fois provoqué, chaque sujet devenait pour lui un texte d'études sérieuses et de découvertes. Jamais il ne lâchait prise qu'après avoir entièrement éclairci la question proposée, soit qu'il la réduisit à rien, soit qu'il en tirât quelque résultat net et substanciel.... Un jour, la solution désirée sembla nécessiter la lecture de l'ouvrage de Leopold sur les machines; Watt apprit aussitôt l'Allemand. Dans une autre circonstance, et pour un motif semblable, il se rendit maître de la langue italienne... La simplicité naïve du jeune ingénieur lui conciliait sur le champ la bienveillance de tous ceux qui l'accostaient." J. ROBISON, cité par F. ARAGO, Watt in Œuvres, t.1
|
Brevetée en 1780, elle fut manufacturée par les établissements Watt & Boulton, qui construisaient les machines à vapeur! Pas moins de 630 exemplaires fiurent vendus la première année, notamment à des célébrités comme Benjamin Franklin et Thomas Jefferson. L'accent commercial était mis sur sa portabilité (une valisette en acajou) et son intérêt pour le secret des correspondances, puisqu'elle évitait de recourir à un secrétaire-copiste.
Voici un autre témoignage de poids, grâce auquel nous apprenons que l'entrée dans la vieillesse navait en rien altéré ses facuktés mentales:
"Watt
n'était pas seulement le savant le plus profond; celui qui avec le plus
de succès avait tiré de certaines combinaisons de nombres et de forces
des applications usuelles; il n'occupait pas seulement un des premiers
rangs parmi ceux qui se font remarquer par la généralité de leur
instruction; il était encore le meilleur, le plus aimable des hommes. La
seule fois que je l'aie rencontré, il était entouré d'une petite
réunion de littérateurs du Nord... Là, je vis et j'entendis ce que je
ne verrai et n'entendrai plus jamais. Dans la quatre-vingt-unième année
de son âge, le vieillard, alerte, aimable, bienveillant, prenait un vif
intérêt à toutes les questions; sa science était à la
disposition de qui la réclamait. [...] Parmi les gentlemen se trouva un
profond philologue; Watt discuta avec lui sur l'origine de l'alphabet,
comme s'il avait été un contemporain de Cadmus. Un célèbre critique
s'étant mis de la partie, vous eussiez dit que le vieillard avait
consacré sa vie toute entière à l'étude des belles lettres et de
l'économie politique. Il serait superflu de mentionner les scie,ces:
c'était sa carrière, brillante et spéciale [...]
Nous découvrimes, enfin, qu'aucun roman du plus léger renom ne lui
avait échappé, et que la passion de l'illustre savant pour ce genre
d'ouvrages était aussi vive que celle qu'ils inspirent aux jeunes
modistes de dix-huit ans."
Sir Walter SCOTT, cité par F. ARAGO, Watt in Œuvres, t.1
|
 |
 |
|
| Walter Scott, sous son gigantesque monument, à Édimbourg (Écosse) |
|||
Et une Statue...
Elle est nichée dans un angle de la James Watt Memorial School,
autre bâtiment remarquable de Greenock, à l'angle de William street, où
se trouvait la maison natale de Watt. Construit en 1908 dans un beau
grès rouge, dans le style baronial écossais
(variante locale du néo-gothique, fort prisé en fin de XIXème siècle,
et dont un célèbre représentant est la résidence royale de Balmoral),
il
avait été financé par... le magnat américain de l'acier, Andrew
Carnegie. Surprenant? Pas vraiment si on y regarde de plus près: il
était d'ascendance écossaise, et avait même écrit une biographie de
Watt, avec un argument imparable pour se justifier:"Pourquoi n'écrirais-je pas sur la vie de celui qui a construit la machine sur laquelle j'ai bâti ma fortune?"
C'était un centre de formation des navigateurs et ingénieurs
(Greenock était alors le siège d'un très important chantier naval);
elle a fermé en 1973. la James Watt Memorial School et la statue de Watt |
 |  |
 |
| Mais... que tient-il donc à la main? Il s'agit d'un appareil indicateur de pression de la vapeur dans une machine, utilisé lors de leur mise au point. Quoiqu'il ait souvent été attribué à Watt (et le sculpteur, en le mettant en vedette, est sans doute le premier à le croire...), ce serait plus sûrement l'invention d'un de ses assistants, John Southern, en 1796. Ce qui est remarquable, c'est qu'il donne son résultat sous la forme d'un tracé graphique! Un cylindre intérieur au "manche" (remarquer le robinet d'admission de la vapeur en bas) fait bouger verticalement la pointe traçeuse, tandis qu'une tablette portant le papier enregistreur coulisse horizontalement sur le cadre-support, mue par le câble attaché au petit cylindre, que l'on fixe sur le piston de la machine. Le tracé qui en résulte a la forme d'un cycle fermé. |
|||
Et par chance, pour mieux comprendre... ce dispositif est visible au Science Museum de Londres, où le Mathouriste l'avait photographié... bien des années auparavant, un peu perplexe devant un descriptif assez sommaire! (Il ne précisait ni qui était Southern par rapport à Watt, ni le fonctionnement...)
 |
 |
Bien d'autres statues de Watt sont présentes au Royaume Uni, nous les évoquerons plus loin dans cette page.
La James Watt Memorial School a une façade sur William Street, pratiquement en face de la maison natale de James.
 |
 |
 |
 |
| William Street (source de l'image) |
Toon-Kirk | autre vue (partielle) deWilliam Street, trouvée sur... | ...le panneau présentant le quartier historique de la ville. Remarquer, en haut et à Gauche, Watt et sa machine à vapeur! |
Cette rue est assez méconnaissable aujourd'hui (d'autant qu'elle était le siège de travaux importants mors du passage de votre serviteur, l'empêchant de réaliser un cliché quon puisse comparer à la gravure!); mais l'église Toon Kirk se dresse toujours au bout, avec la fontaine devant. Elle pouvait accueillir jusqu'à 1600 fidèles, selon un aménagement intérieur dû au père de l'ingénieur, James Watt Sr.
Le fameux Mécanisme, le Parallélogramme... et la Géométrie!
Watt a conçu (et commercialisé avec Boulton) uniquement des
machines statiques, essentiellement destinées au pompage dans les
mines. Leur développement , parsemé de nombreuses améliorations,
s'étent de 1765 à 1790. Mais pour présenter le problème mécanique qu'il
a brillament résolu, un petit bond en avant dans le temps, en 1830, et
dans l'espace en nous transportant au fabuleux Musée des Chemins de Fer
de York (Angleterre) permet de visualiser très simplement le problème:Comment transformer le mouvement linéaire d'un piston en mouvement circulaire d'une roue?
 |
 |  |
 |
| Premier train de voyageurs de l'histoire: 15 septembre 1815, ligne Liverpool-Manchester sous l'œil de son inventeur... |
...George Stephenson | Sa locomotive, la célèbre "Rocket" Le piston, la bielle, et la manivelle |
Voiture "fermée" affichant fièrement la ligne! Derrière, voiture ouverte (un simple tombereau) |
Le système adopté est le classique couple "bielle-manivelle" : le piston pousse et tire une tige longue (la bielle), qui agit sur une tige courte solidaire de l'essieu moteur, la manivelle. Ainsi, le vaet-vient assez limité de la tige du piston peut entraîner un tour complet de la roue.
Mais ce système rudimentaire a un défaut: il ne réalise pas exactement cette transformation, et la bielle à tendance à "forcer" la tige du piston par un déplacement latéral parasite: sans bague de guidage à la sortie du cylindre, la tige du piston irait de biais (au lieu de suivre parfairement l'axe du cylindre); et la bague , si elle est présente, sera très rapidement usée par le frottement en résultant, et cassée!
La solution (approchée seulement, on le verra) proposée par l'ingénieur écossais -celle de ses inventions dont il se disait le plus fier- est souvent dénommée en raccourci parallélogramme de Watt. Mais ce nom même peut induire en erreur, car il n'y a pas que le parallémograme, pnlutôt bien visible.
 modèle (1813) présenté au Science Museum de Londres, qui aurait appartenu à Watt En haut et à gauche, le fameux parallélogramme;
en bas et au centre, le régulateur à boules; à droite, le couple bielle-manivelle entraînant la roue sous l'oscillation du balancier. |
 modèle présenté au musée de Greenock |  son paralélélogramme |
| "La
solution qu'il a donné de cet important problème est peut-être sa
plus ingénieuse invention. Parmi les parties constituantes de la
machine à vapeur, vous avez sans doute remarqué certain parallélogramme
articulé. À chaque double oscillation il se développe et se resserre,
avec le moelleux, j'ai presque dit avec la grâce qui vous charme dans
les gestes d'un acteur consommé. Suivez attentivement de l'œil ses
diverses transformations, et vous les trouverez assujetties aux
conditions géométriques les plus curieuses; et vous verrez que trois
des angles du parallélogramme
décrivent dans l'espace des arcs de cercle, tandis que le quatrième, le
sommet de l'angle qui soulève et abaisse la tige du piston se meut à
très peu près en ligne droite. L'immense utilité du résultat frappe
encore moins les mécaniciens que la simplicité des moyens avec lesquels
Watt l'a obtenu." F. ARAGO, Watt in Œuvres, t.1
|
||
Cette appellation, parallélogramme de Watt, est un peu trompeuse, car l'ensemble mécanique consiste en la mise en série de deux dispositifs:
 paralélélogramme seul |  le mécanisme de Watt |
|
 |
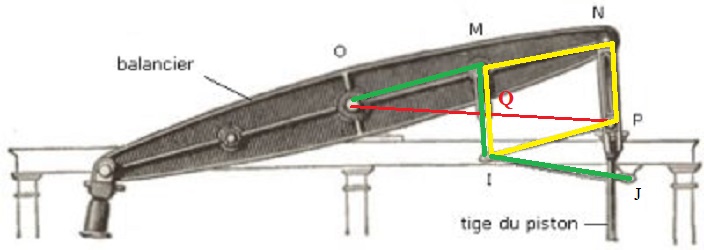O étant fixe, M décrit (une portion de cercle, et de même pour I puisque J est fixe. La question se reformule donc ainsi: Q décrit-il une portion de droite? Et si c'est le cas, P fera de même par hoùothétie, et le risque d'usure et de casse de la bague de guidage au sommet du piston disparaîtra.
Pour l'aspect expérimental de la réponse, voici deux modèles, réalisés par le musée de Modène, à l'initiative de F. Conti: le premier, disposé sur un plan horizontal, trace la courbe complète effectivement parcourue par le point Q, tandis que le second, vertical, permet de constater l'efficacité pour des mouvements circulaires limités des deux grands bras (comme c'est le cas pour le balancier d'une machine à vapeur statique).
 |
 |  |
 |
"J'ai
été moi-même surpris de la régularité de son action. Quand je l'ai vu
marcher pour la première fois, j'ai eu véritablement tout le plaisir de
la nouveauté, comme si j'avais examiné l'invention d'une autre
personne." J. WATT cité par F. ARAGO, Watt in Œuvres, t.1
|
|
| On
constate effectivement une longue portion de "ligne droite" (pas tout à
fait, mais c'est à peine perceptible) en lançant le tracé; mais la
courbe complète est une lemniscate, une sorte de nœud papillon, si l'on préfère. Et non, ce n'est pas la très célèbre lemniscate de Bernoulli: cette dernière est du quatrième degré, tandis que celle qu'on vient de tracer, et qui fut baptisée courbe de Watt (évidemment!) est, elle du sixième degré.  On l'appelle parfois, plus prosaïquement, courbe à longue inflexion. Pour en savoir plus mathématiquement, et voir des animations, reportez-vous, comme d'habitude, à l'encyclopédie des courbes en ligne de Robert Férreol. |
||
Mais peut-on voir, en vrai, ce mécanisme à trois barres sur une machine à vapeur, sans le parallélogramme? La réponse est OUI, ... et se trouve au National Railway Museum d'York!
 |
 |  |
|
Ce
monstre de 1833, installé au sommet d'une colline, avait bien pour
fonction d'y faire grimper des wagons lourdement chargés (charbon,
bois, blocs de calcaire pour la construction...). Mais en restant fixe au sommet, en tirant le train à l'aide d'un câble qu'elle enroulait sur un tambour (elle est pour cette raison dénommée winding engine).
On mesure grâce à elle l'intérêt du parallélogramme: en son absence, les deux bras doivent être très longs! L'astuce de Watt a permis, pour une même amplitude verticale résultante, de diviser par deux la longueur de ces bras, et la machine obtenue est bien plus compacte. |
||
Cette excellente solution industrielle laissait cependant ouverte la question théorique: peut-on construire un mécanisme de tiges articulées réalisant de manière exacte la transformation d'un mouvement circulaire en mouvement linéaire?
| La question passionnait le russe Tchebychev, constructeur de nombreux mécanismes, mais qui échoua à la résoudre. Ce qui est heureux, d'une manière pour le moins imprévue, car c'est ce qui le conduisit à sa théorie des meilleures approximations uniformes en analyse. Ou comment un problème de mécanique pratique a donné naissance à de très belles recherches théoriques, et voilà donc un joli sujet pour une méditation philosophique! |  | 
|
| Un mécanisme de Tchebychev: on remarque la partie quasi droite du tracé. | Timbre russe célébrant Tchebychev, avec un de ses mécanismes. |
 |
Et pourtant, une solution exacte existe bel et bien, et elle a été découverte en 1868 par un officier du génie français, polytechnicien, Charles Peaucellier
(1832-1919), et retrouvée 3 ans plus tard, indépendamment, par le
Lituanien Lipkin (1840-1876). Lequel a été plus célébré en URSS que
Peaucellier en France, soit dit en passant... Elle repose sur une tranformation géométrique classique, l'inversion, qui a justement la propriété de transformer les droites en cercles. Qu'on avait le bon goût d'étudier avant le bac aux beaux temps de la Terminale C! Et c'est pourquoi le mécanisme est souvent qualifié d'inverseur de Peaucellier. |
|
 |
 |  |
| Premier train de voyageurs de l'histoire: 15 septembre 1815, ligne Liverpool-Manchester sous l'œil de son inventeur... |
...George Stephenson | Sa locomotive, la célèbre "Rocket" Le piston, la bielle, et la manivelle |
Un autre résultat liant théorie et pratique prolonge cette histoire... La courbe de Watt, on a pu le voir ci-dessus, est une courbe algébrique, c'est à dire que
son équation est de la forme P(x,y) = 0, où P est un polynôme à deux variables.
| De même, tout système articulé trace une courbe algébrique, et, encore plus remarquable, inversement, pour toute courbe algébrique, il est possible de trouver un système de tiges articulées qui la trace! C'est le théorème de Kempe (1879) Son auteur (1849-1922) est un anglais, élève de Cayley, et il précisait dans son article: "Il reste cependant un large champ ouvert à l'artiste mathématicien pour découvrir les liaisons les plus simples qui décriront des courbes particulières" Concrètement, on a pu facilement donner des mécanismes simpes construisant les coniques, ainsi que d'autres courbes. D'après le théorème, nous avons, par exemple, la certitude qu'il en existe pour la lemniscate de Bernoulli citée plus haut (puisqu'elle est algébrique de degré 4), et une certitude non loins forte: qu'il n'en existe pas pour la chaînette y = ch x , qui n'est pas algébrique. |
 Le début de l'article de Kempe |
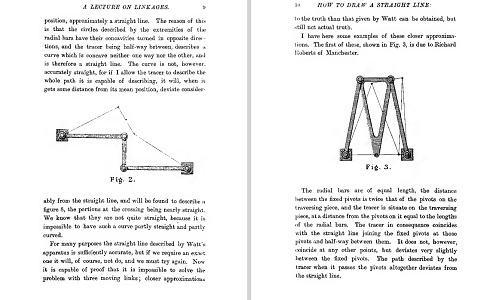
Kempe a développé le sujet dans une conférence, publiée avec de nombreuses figures:
|
 |  |
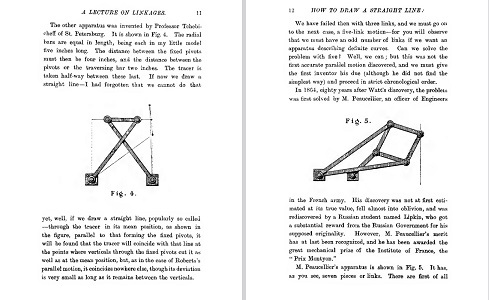
| Le mécanisme de Watt, bien sûr, mais aussi celui de Roberts. | Les mécanismes de Tchebychev et Peaucellier. C'est lui qui signale que Lipkin fut plus honoré par son pays! |
De leur côté, les locomotives ont bien évolué... avec des embiellages nettement plus complexes. Ci-dessous, deux "sommets" inégalés, l'un français, l'autre anglais, si différents dans leurs esthétiques...
 |
 |
 |
| Super-Pacific 231E, le chef d'œuvre du génial ingénieur André Chapelon Cité du Train, Mulhouse |
Sa distribution Walschaerts (du nom de l'ingénieur belge Égide Walschaerts) |
la "Mallard", recordwoman de vitesse vapeur (202km/h) National Railway Museum, York (Angleterre) |
Et quoi de meilleur, pour en apprécier le mouvement, que de regarder la Pacific 231E24 en action, dans l'excellent court métrage de Jean Mitry (1949) sur la musique d'Arthur Honneger (1923)?
arrêt sur image du film
Watt else?
< sera complété prochainement>
Références
N.B. : le livre dont nous avons adjoint l'image, acheté au musée, a été une très riche source d'informations complémentaires aux cartels de l'exposition. [source de l'illustration]Sa couverture reproduit un tableau de 1792, de C.F. Von Breda, "James Watt assis à côté d'un schéma de machine à vapeur" (Science & Society Picture Library); vous pouvez l'aggradir par clic, ce qui vous offre un deuxième tableau avec Watt pour sujet.
|
 |
Revenir
à la Home
Page du
Mathouriste