En 1870, on érige au centre de la Markt-Platz (place du marché) un monument à l'enfant du pays, celui qui, entre Copernic et Newton, aura fait basculer avec eux deux la Mécanique Céleste de la cosmologie antique à la vision moderne.

     

Son intérêt pour les astres est précoce: il n'a que 6 ans quand sa mère l'emmène voir, du sommet d'une colline, la comète de 1577; un peu plus tard, son père lui dfera observer une éclipse de lune.


Après sa scolarité élémentaire, Johannes, qui se verrait bien pasteur luthérien, part étudier au séminaire de Maulbronn, tout près de Weil. 

	"Le Collège de Maulbronn était un ancien monastère cistercien que le grand-duc de Wurtemberg avait confisqué lorsqu'il s'était converti à la foi luthérienne, une trentaine d'années auparavant. Perché en haut d'un piton triangulaire où jadis jaillissait une source, ce quadrilatère de hautes bâtisses avait toutes les allures d'un château-fort entouré de profonds fossés. On murmurait que jadis, le fameux docteur Faust y avait été l'alchimiste d'un des abbés. On racontait aussi que, plus longtemps auparavant, le Diable s'était fait moine et avait incendié ce qui avait été la plus grande bibliothèque du monde." J.-P. Luminet, La Discorde Céleste
			une autre vue sympathique, recto-verso, du monastère de Maulbronn, trouvée, comme on s'en doutera, à proximité immédiate...
			Le jeune séminariste fut sans doute, comme ses condisciples, impressionné  par l'austère et  grandiose  beauté des lieux (aujourd'hui considéré comme le plus complet des ensembles monastiques européens, le monastère figure sur la liste du patrimoine mondial de l'humanité) . Le mélange d'arcs romans et gothiques, qui peut surprendre au premier abord, est caractéristique de l'époque de transition entre les deux styles. Site web du monastère de Maulbronn Maulbronn sur Wikipedia pour préparer votre visite!

Le cloître, exceptionnel,  invite autant à la méditation intérieure qu'à la contemplation géométrique, par les nombreux arcs de cercles qui le décorent...

Le portail roman (1178)			Le "Paradis" (porche d'entrée)

		Kepler séjourne à Maulbronn de 1586 à 1589, avant d'aller étudier à l'université de Tübingen: là, les choses sérieuses vont vraiment commencer pour lui, du moins en ce qui concerne l'astronomie : il va se découvrir un maître, Michaêl Mästlin (1550-1631).
		à gauche : Tübingen, gravure ancienne. L'université est repérée par C. à droite : Mästlin, dans une des niches du socle du monument Kepler à Weil

Mästlin, sur le socle  du monument Kepler à Weil

"Kepler dévisage avec émotion le magister de sa première heure de cours. L'homme a le cheveu pauvre, l'air triste et inquiet et pourtant jovial. Il est affublé d'une barbichette de noble sur un visage de paysan. Son corps est sec comme un sarment. Johannes le reconnaît. En furetant chez Gruppenbach, il a découvert un traité d'astronomie signé Maestlin, professeur de mathématiques à l'université de Tübingen. Il paraît sortir de la gravure qui le représentait devant une tenture sombre, un compas à la main, à côté d'un globe ressemblant à un crâne. [...] « [...] j'ai à vous dire que vous viendrez à mon cours pour parfaire votre intelligence, en faire quelque chose de subtil! Les mathématiques sont là pour charpenter votre esprit, et non l'appesantir. C'est une science qui ne flatte ni ne feint.»" H. Chardak, Johannes Kepler

Mästlin, portrait à l'université deTübingen, (photo à Weil, ) C'est le portrait auquel le texte ci-contre se réfère.

Un deuxième relief du socle, sur le monument de Weil, nous fait voir Mästlin, prenant par la main le jeune Kepler: l'allégorie est poussée au point de représenter ce dernier, davantage comme un collègien plutôt qu'un étudiant. Derrière eux, les deux bustes des pères fondateurs de l'astronomie, Hipparque (le plus à l'avant) et Ptolémée (à l'arrière).
Et Mästlin montre, de sa main... il montre...IL MONTRE....

Alors que Mästlin enseigne, très officiellement, le système géocentrique de Ptolémée, il fait découvrir à ses disciples, plus secrètement, mais avec un grand enthousiasme, celui de Copernic! Car, entre 1550 et 1600 (en gros), l'église luthérienne est beaucoup plus hostile à l'héliocentrisme (Luther a qualifié Copernic de fou qui contredit l'Écriture) que la Papauté, qui le tolère comme hypothèse de calcul si elle apparaît plus commode, à la condition expresse de la dissocier de la "réalité". Tout changera quand, effrayée des progrès du protestantisme, l'Église catholique intensifiera la Contre-Réforme: l'ouvrage de Copernic ne sera mis à l'index qu'en 1616, Galilée ne devra abjurer l'héliocentrisme qu'en 1633. N.B. : la réception du travail de Copernic est détaillée, de manière plus précise, dans notre page nonsacrée au De Revolutionibus.
Le nom est inscrit en haut du relief, le soleil est au centre d'orbites représentées circulaires (conformément aux prmières figures, simplifiées, de Copernic lui-même), et les diverses lunes de Jupiter ou Saturne (la plus lointaine connue à cette époque) sont figurées. Copernic lui-même est montré sans une niche d'angle, tenant une tablette où est dessiné son système.

Mystère à Graz

" Il se prépare à passer son examen théologique de 1594 qui lui permettra de prêcher. Mais ses maîtres en ont décidé autrement. Le lendemain de son vingt-deuxième anniversaire, au lieu de la nomination eccliésiastique promise dans le Wurtemberg, Kepler est officiellement et cruellement sollicité par les États de Styrie pour le poste de Mathematicus de la Stiftschule de Graz. La Styrie autrichienne et catholique vient de perdre son professeur de mathématiques, le protestant Georg Stadius, et c'est une aubaine pour des maîtres frileux qui veulent envoyer leur brillant élève en enfer! " H. Chardak, Johannes Kepler

" À Graz, l'enseignement, d'un niveau assez bas, l'ennuyait; d'ailleurs il n'avait presque pas d'élèves. Les travaux auxquels sa charge de mathématicien des États de Styrie l'obligeait, consistaient à établir des calendriers  et  des  horoscopes, et n'avaient rien de plus enthousiasmant. Du moins lui laissaient-ils des loisirs pour ses recherches personnelles et ses méditations extatiques.sur la structure de l'univers.  Le Mysterium Cosmographicum, qu'il  écrivit en 1595, et publia, grâce au soutien de Maestlin, en 1596, fut le fruit de ces méditations. " A. Koyré, La Révolution Astronomique: Copernic, Kepler, Borelli

 
Dans un extravagant mélange de mysticisme et d'esthétisme, Kepler y présente l'univers comme construit par un Dieu Géomètre: les sphères sur lesquelles se meuvent chacune des 6 planètes (de Mercure à Saturne, selon les connaissances de son temps, qui ne diffèrent pas, sur ce point, de celles de l'Antiquité) s'emboîtent parfaitement dans un enchaînement des cinq polyèdres réguliers (ou solides platoniciens), tangentes intérieurement à l'un et circonscrites à l'autre. L'ouvrage contient une magnifique illustration en perspective, et un modèle en métal en a été réalisé en 1930, qui est pour le Mathouriste le clou de l'exposition du musée de Weil der Stadt.

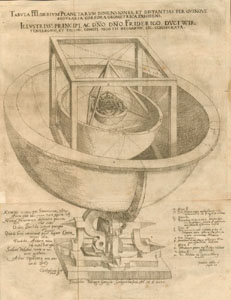
page de titre du Mysterium Cosmographicum	la célèbre figure	Modèle de Hermann Müller (Stuttgart) Musée Kepler, Weil der Stadt

Voici comment il s'exprime:
    

" [La sphère de] la Terre est la mesure pour toutes les autres sphères. Placez autour, tangentiellement,  un dodécaèdre, et la sphère qui lui est circonscrite sera celle de Mars. Tangentiellement à celle-ci, placez un tétraèdre, et la sphère circonscrite sera celle de Jupiter; enfin disposez tangentiellement à celle-ci un cube, et la sphère circonscrite sera celle de Saturne. À présent, placez à l'intérieur de la sphère de la Terre un icosaèdre tel qu'elle lui soit circonscrite; la sphère tangente intérieurement sera celle de Vénus; inscrivez y un octaèdre, la la sphère tangente intérieurement sera celle de  Mercure. Et voilà ce qui explique le nombre des planètes. " J. Kepler, Mysterium Cosmographicum

Oui, vous avez bien lu: il y a 6 planètes seulement, parce qu'il n'y a que 5 polyèdres réguliers, et qu'on les intercale en commençant et finissant par une sphère! Certes, il a comparé les distances des planètes au soleil à celle se sa construction géométrique, avec pour résultat un accord assez lâche, qu'il aurait dû en toute logique considérer comme peu convaincant. C'est faux, mais que c'est beau!

		à gauche :  Cube et tétraèdre sont bien en évidence..
		à droite : à l'intérieur du tétraèdre, on rencontre d'abord  le dodécaèdre (12 faces pentagonales), à l'intérieur de celui-ci, l'icosaèdre (20 faces triangulaires équilatéralales) au plus profond, on devine l'octaèdre

Comment un point de départ aussi farfelu va-t-il, petit à petit, évoluer vers une théorie rigoureuse? C'est ce que va nous apprendre la suite de l'histoire. Mais on peut au moins, à ce stade, savoir comment lui est venue cette idée, car il nous dévoile son inspiration, allant même jusqu'à dater le jour de son Eureka personnel:

Grande  Conjonction du 21/12//2020 ( Source NASA, sur le site Futura-Sciences )

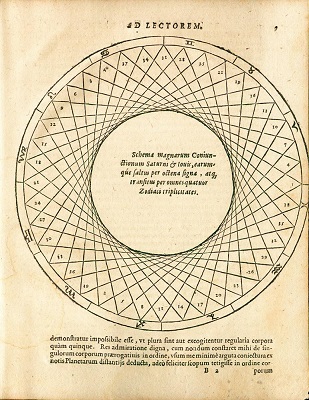" Cela advint le 9, ou le 19 juillet 1595. Je souhaitais montrer à mes étudiants comment les grandes conjonctions sautent huit signes zodiacaux et passent successivement d'un triangle à un autre. Je dessinais un grand nombre de triangles (si on peut les appeler ainsi) dans un cercle, de telle manière que la fin de l'un soit le début du suivant. Alors, les points en lesquels s'intersectent ces trianglesforment un petit cercle; car le rayon du cercle inscrit à un trl triangle est moitié du rayon du cercle circonscrit. Le rapport entre les deux cercles était, à vue, exactement le même que celui qu'on trouve entre [les orbites de] Saturne et Jupiter; et le triangle est la première des figures géométriques, tout comme Saturne et Jupiter sont les premières  des planètes. J'essayai immédiatement d'ajuster la deuxième distance, de Mars à Jupiter, au moyen d'un carré, la troisième à l'iade d'un pentagone, la quatrième au moyen d'un hexagone" J. Kepler, Mysterium Cosmographicum

Quelques précisions... s'imposent, à commencer par une définition astronomique; mais pourquoi ne pas la laisser au soin d'un romancier (bien documenté)?

"Christina se tut un instant, songeuse, puis reprit: - Il doit se passer quelque chose sur la Lune au moment d'une conjonction des planètes Jupiter et Saturne, elle -même en quadrature avec le Soleil. Et ce moment doit approcher puisqu'Elena a commencé son observation hier. - Qu'est-ce qu'une quadrature et une conjonction? demanda Angélique, l'air complètement dépassé. - Une conjonction est l'alignement de deux planètes par rapport à la Terre, ou, dans ce cas-ci, peut-être par rapport à la Lune, répondit Christina.C'est comme si l'on voyait les deux planètes l'une derrière l'autre. Une quadrature, quant à elle, appparaît lorsqu'un angle de quatre-vingt dix degrés se présente dans l'espace entre deux corps célestes." B. Sagaro, La Conjonction Dorée (2020)

Comme il s'agit d'une circonstance exceptionnelle, elle a toujours été interprétée comme un signe d'évènement extraordinaire par les astrologues. D'où l'expression restée dans le langage populaire, pour un ensemble de coïncidences heureuses: "les planètes étaient alignées".
Les périodes de Jupiter et Saturne étant respectivement de 11,9 et 29,5 années, elles se  produisent otous les 19,86 ans: si l'on arrondit les périodes à 12 et 30 ans pour faire plus simple, les trois planètes occuperont la même position au bout de 60 ans, car 12×5 = 30×2 = 1×60. Mais, tous les 20 ans, Saturne et Jupiter retrouveront la même position relative, Saturne ayant accompli 2/3 tour sur son orbite et Jupiter 5/3 tour = 2/3 + 1 tour. 3 conjonctions successives dessineraient alors un triangle équilatéral parfait. En raison du petit écart avec notre arrondi (trop beau pour être vrai!), le triangle ne se referme plus exactement, et cette même figure va se reproduire, mais en ayant tourné légèrement, de quelques degrés: on a colorié ci-dessous, en rouge, puis vert, puis bleu les trois premiers "triangles" ( "si on peut les appeler ainsi", précise à juste titre l'auteur) de la suite que construit et numérote Kepler, soit 180 ans de conjonctions. Si, pour un triangle équilatéral parfait, le cercle central est exactement de rayon moitié, ce ne sera plus tout à fait exact ici (contrairement au mot employé par Kepler!); mais il est évident que l'on a toujours un cercle, puisque les triangles se déduisent les uns des autres par rotation.
 

Comprenant qu'il fait fausse route en employant les polygones réguliers, Kepler croit avoir l'illumination:

" La fin de cette tentative malheureuse fut le point de départ de la suivante, qui réussit. Je compris qu'en fait, si je voulais poursuivre ainsi l'agencement des figures, je ne parviendrais jamais au soleil, et que je trouverais jamais la raison pour laquelle il y a six planètes, plutôt que vingt ou cent. [...] Je me dis alors que j'obtiendrais ce que je cherchais, si cinq figures particulières, parmi l'infinité des possibles, pouvaient être mises en relation par leur taille avec les six sphères de Copernic. Alors, je fis un pas supplémentaire. Qu'avaient à faire les figures planes avec les sphères des corps célestes? Il fallait clairement avoir recours à des solides. Voici donc maintenant, cher lecteur, ma découverte et le contenu de ce court traité. Quiconque possédant un bagage minimum de géométrie pensera immédiatement aux cinq polyèdres réguliers et à leur relation avec leurs sphères inscrites et circonscrites." J. Kepler, Mysterium Cosmographicum

 Kepler envoie des copies de son livre à Galilée, qui lui fait part de son admiration, et à Tycho Brahé. Le grand astronome Danois est installé à Prague depuis juin 1599, et Kepler se verrait bien devenir son assistant. D'autant que la catholique Graz est de plus en plus invivable pour un protestant...  aussi, quand  Tycho l'invite à le rejoindre, il n'hésite pas; le 1er  janvier 1600, il  quitte Graz.  Son livre a fait mouche!

" - Père, quand arrive-t-on chez grand-papa?  - Dans une heure à peu près. Mais quand je reviendrai vous chercher, au printemps, ton voyage durera aussi longtemps que celui des Argonautes. Veux-tu que je te raconte la légende de Jason parti conquérir la Toison d'Or?  - Un jour, jolie amazone, tu raconteras celle de Kepler allant s'emparer du trésor de Tycho, ajouta le baron Hoffman.  - Qui est donc ce Tycho, dont vous parlez tout le temps, Monsieur le baron? demanda la petite fille.  - Tycho, c'est le Goliath de l'Astronomie. Et ton père, mon enfant, c'est le roi David. " J.-P. Luminet, La Discorde Céleste

À Prague, les Années capitales

"Le philosophe vraiment utile aux progrès des sciences, est  celui qui réunissant à une imagination profonde, une grande sévérité dans le raisonnement et dans les expériences, est à la fois tourmenté par le désir de s’élever aux causes des phénomènes, et par la crainte de se tromper sur celles qu’il leur assigne. Kepler dut à la nature, le premier de ces avantages et Tycho-Brahé lui donna pour le second, d’utiles conseils dont il s’écarta trop souvent , mais qu’il suivit dans tous les cas où il put comparer ses hypothèses aux observations; ce qui, par la méthode d’exclusion, le conduisit, d’hypothèses en hypothèses, aux lois des mouvemens planétaires . Ce grand observateur qu’il alla voir à Prague, et qui dans les premiers ouvrages de Kepler, avait démêlé son génie à travers les analogies mystérieuses des figures et des  nombres, dont ils étaient pleins, l’exhorta à observer, et lui procura le titre de mathématicien impérial." P.-S. de Laplace, Précis de l'Histoire de l'Astronomie ci-contre: modèle en plâtre peint, à l'École Polytechnique (réplique, en plus petit, du monument à Beaumont sur Auge, sa ville natale)

Prague: le couvent Saint Emmaus, et les flèches de son église, Sainte Marie des Slavons

Kepler s'esr installé dans ce couvent, de son arrivée à 1604. Les superbes flèches en coques minces de béton nexistaient pas encore; gageons qu'elles auraient plu à cet esthète de la géométrie. Elles sont l'heuruex dénouement d'un bombardement malheureux de l'aviation américaine en 1945 (une erreur? il n'y avait pas d'objectif stratégique aux alentours...). Elles ont été imaginées par l'architecte F. Černý et inaugurées en 1990.
De 1604 à 1607, il demeura au Collège du Roi Wenceslas (Le bâtiment n'existe plus, il se situait à l'adresse Ovocny trh 12/573). Nous visiterons, plus loin, le dernière maison praguoise où a vécu Kepler.

Assistant de Tycho Brahé

Personnage haut en couleur (Si Otto Preminger en avait fait un film, il se serait appelé L'Homme au Nez d'Or, en référence à la prothèse cachant les séquelles d'un duel), Tycho Brahé (1546-1601) est le meilleur -et le dernier- observateur à l'œil nu de tous les temps. Grâce à ce talent, il a constitué un recueil d'observations exceptionnel, tant par le nombre que la précision; et c'est ce que convoite Kepler. Il ne tarde pas à juger son nouveau patron, rencontré pour la première fois le 4 février 1600.

" Voilà ce que je pense de Tycho: il nage dans les richesses, mais il ne sait pas les exploiter de mannière correcte, comme c'est le cas de la plupart des gens riches. Il faudrait donc essayer de les lui soutirer (et moi même, modestement, j'ai joué mon rôle) en mendiant presque, pour que ses observations soient divulguées de manière sincère et complète. " J. Kepler, lettre à Mästlin, février 1599

Tycho, sur le socle de Kepler à Weil

Prague, bien sûr, se souvient de cette collaboration, pourtant réduite à moins de deux ans, avec ce beau monument (1984) du sculpteur Josef Vajce (1937-2011). L'esprit de chacun des héros est bien capté: à Tycho le grand instrument de visée, à Kepler les feuilles de papier, qu'on imagine couvertes de calculs...


Le décor vous suggèrera l'optimalité d'une visite au printemps, stratégie choisie par le Mathouriste ... mais Prague est belle en toute saison, qui ne le sait pas? Même s'il n'est pas au centre ville, vous le trouverez facilement: vous ne manquerez sûrement pas de visiter le monastère Strahov et sa magifique bibliothèque. Et pour y monter... vous emprunterez probablement la bien nommée rue Keplerova; un peu avant votre but, à gauche, à l'angle du lycée Kepler (alias Gymnázium Jana Keplera, comme écrit sur lenseigne en ahhaur de la porte), dont un mur est derrière nos héros: c'est là!

Dans l'entrée du lycée, une plaque rappelle que c'est sur e terrain qu'était bâtie la maison, de style Renaissance, où logeaient Tycho et sa famille. Il envisageait d'y aménager un observatoire, mais il n'en a pas eu le temps.

Mais revenons à notre tandem. Travailler avec Tycho n'est pas si facile, non seulement parce qu'il garde jalousement scellés ses relevés, mais aussi parce qu'il s'entête à conserver son propre système cosmographique, intermédiaire entre Ptolémée et Copernic: pour lui, le Soleil tourne autour de la Terre (comme chez Ptolémée), et toutes les autres planètes autour du Soleil: un joli ballet céleste! Et ce ne sont pas ses excellentes mesures qui pouvaient lui faire abandonner cette idée saugrenue: comme il ne s'agit, pour passer dun système à l'autre, que de changements de repères, chacun des trois modèles est également prédictif!
Ci-contre, page de titre du traité sur la Lune, Selenographia,  de l'astronome Jan Heweliusz. Il contient une description et une figure du système de Tycho. Nous avons rajouté le point jaune figurant la position du Soleil qui sert de centre aux cinq autres planètes; ce point tournant autour de la Terre, les 5 orbites se retrouvent entraînées dans ce mouvement, engendrant "naturellement" des trajectoires épicycliques, dont le déférent est l'orbite solaire.
		Jan Heweliusz (1611-1687) Astronome polonais, né à Gdansk, il a étudié à Paris, y a rencontré Mersenne. Ils ont ensuite continué à correspondre. Il est ici statufié à Gdansk.

Brahé, qui a vite évalué les exceptionnelles capacités de son second, lui confie le calcul de l'orbite de Mars. Quelque peu présomptueux, Kepler affirme que ce sera l'affaire de quelques jours... puis de quelques semaines. Il en aura pour six ans! Mais il ne vieilliront pas ensemble, car le Danois meurt le 24 octobre 1601.
Un dicton, à Prague, court sur les lèvres qu'humidifie la généreuse mousse de la bière: "Je ne veux pas mourir comme Tycho Brahé." Façon pour votre interlocuteur de vous glisser dans un sourire qu'il va aller se soulager aux toilettes entre deux choppes! Les doctes reconstitutions médicales , quelques sècles après, oscillent encore entre infection urinaire et éclatement de la vessie tout en s'accordant sur la circonstance initiale d'un repas trop copieux -Kepler lui-même l'a affirmé. Laissons nous conter la légende, un peu plus truculente:

" - Je vais vous le prouver, Monsieur le Conseiller. Abandonnons ce Tokay, qui ne convient qu'aux femmes et aux Italiens. Je vous parie, Messieurs, une coucherie avec ma fille Céline contre un tonneau de vin français que je peux boire coup sur coup six pintes de bonne bière de mon ami Scultetus, et que je reste ensuite une heure en contenant mon eau! - Six pintes? Une heure sans pisser? C'est impossible! s'exclama le baron. Vous allez éclater! Je m'y refuse.- - Pourquoi, grinça Tycho, ma chaste Cécile ne vous convient-elle pas? Les préférez vous un peu plus expérimentées, comme Sophie la sage? [...] Mais j'ai mieux encore! Faute de Cythère, que diriez vous de'un voyage à Lesbos? Mon ainée Madeleine vous y conviera. Désolé, Monsieur le baron, de ne pouvoir vous offroir ma femme. Une paysanne encore crottée... D'ailleurs, elle ne vaut rien dans le déduit. Croyez moi, je sais de quoi je parle. [...] Jugeant qu'il était temps de faire partir ses invités, le baron vint lui tapoter l'épaule: - La journée a été éprouvante, cher ami, allons nous reposer. Tycho se redressa, le nez de travers, frappa du poing contre la table et lança: - Ah, non! Je vous ai lancé un défi, je le tiendrai. Six pintes, une heure  sans pisser. [...] Ils se goinfrèrent pendant une heure. Puis, par défi, Tycho attendit encore cinq minutes avant de se diriger vers le laquais porteur d'un seau d'aisance. Rien ne vint.[...]Il se sentait balloné, une vague douleur lui pesait dans les reins. Il décida de rentrer seul, à pied, par les jardins, estimant que cette belle nuit d'octobre klui ferait le plus grand bien. - Et puis, ajouta-t-il, un sycomore ou quelque autre essence rapportée des Indes inspireront ma vessie. Adieu, Messieurs, [...]  Son envie d'uriner devenait douloureuse. Faute de sycomore, il essaya sous un orme. En vain. Il songea que la Lune était en conjonction avec Saturne. " J.-P. Luminet, La Discorde Céleste

Son agonie durera une douzaine de jours. Sentant sa fin proche, c'est Kepler qu'il fait appeler à son chevet:

" À un moment, Brahé se soulève et hurle:  - Kepler, approche et jette-moi tout ce monde dehors, j'ai à te parler. Sans attendre, il continue à voix basse! - Promets moi d'achever mon catalogue, mes tables surtout... Dieu, que ma langue est sèche! Tant pis, je veux encore boire, à m'en éclater. Du vin, pour un homme plein d'eaux. Ah, Kepler! Que je ne parraisse pas avoir vécu en vain. Kepler, ne frustra vixisse videor. Tu vas t'atteler à la tâche; l'œuvre de Brahé, tu l'accompliras jusqu'à la fin. Jure! - Je jure devant Dieu d'achever ton œuvre. Je te le promets." H. Chardak, Johannes Kepler

Brahé repose depuis à Notre Dame de Tynn, au centre de Prague.

Night and Day sur Notre Dame de Tynn; à l'intérieur, la dalle ancienne (redressée) de la sépulture de Tycho et la récente insciption au sol

Voilà donc Kepler seul maître à bord, d'autant que Brahé a assuré sa position en le faisant nommer Astronome Impérial de Sa Majesté Rodolphe II.

Astronome Impérial

"La mort deTycho, arrivée peu d’années après, mit Kepler en possession de la collection précieuse des observations de son illustre maître; et il en fit l’emploi le plus utile, en fondant sur elles, trois des plus importantes découvertes que l’on ait faites dans la philosophie naturelle. Ce fut une opposition de Mars, qui détermina Kepler à s’occuper de préférence, des mouvemens de cette planète. Son choix fut heureux, en ce que l’orbe de Mars étant un des plus excentriques du système planétaire, et la planète approchant fort près de la-terre, dans ses oppositions, les inégalités de son mouvement sont plus grandes que celles des autres planètes, et doivent plus facilement et plus sûrement en faire découvrir les lois." P.-S. de Laplace, Précis de l'Histoire de l'Astronomie

Ce n'est cependant pas le seul sujet dont s'occupe Kepler. Il y a les rendez-vous astronomiques à ne pas manquer (conjonctions, oppositions, quadratures), car ils permettent des relevés intéressants; et c'est le ciel qui les fixe! Il y a  aussi les surprises qui peuvent, si l'on ose dire, se présente...conjointement! C'est en guettant la grande conjonction de Jupiter et Saturne  (rappelez-vous le début du  Mysterium Cosmographicum) que Kepler, alerté par un astronome tchèque, Brunovski, qui l'a vue le premier, découvre une étoile nouvelle dans la Constellation du Serpentaire, le 17 octobre 1604. Nous savons aujourd'hui qu'il s'agit de l'explosion d'une supernova: les idées d'Aristote, qui faisaient référence, et au premier chef dans les milieux religieux, sont désormais caduques: les Cieux ne sont pas immuables!
D'ailleurs, Tycho avait relevé un phénomène semblable en 1572: un observateur de sa classe ne pouvait y manquer. Bref, après avoir convié l'Emprereur à mettre lui-même l'œil à la lunette pour constater l'évènement (et, peut-être, l'interpréter avec roublardise comme un heureux présage pour la suite de son règne), Kepler se met à écrire; ce sera son premier  traité publié à Prague (en ligne sur e|rara). 

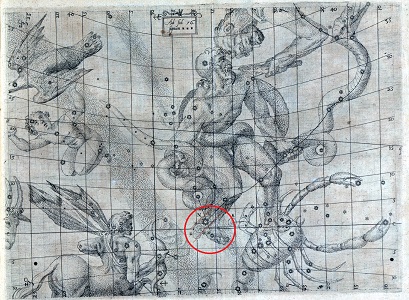
page de titre du De Stella Nova	Carte céleste insérée dans le traité.'étoile nouvelle, notée N par Kepler, est dans la zone que nous avons entourée en rouge.	Kepler et son facteur d'instrument, Jöst Bûrgi sur le socle du monument Kepler à Weil der Stadt

Il est temps de présenter le quatrième et dernier personnage à figurer dans un angle du monument de Weil der Stadt, qui est aussi celui que le relief montre, observant dans la lunette à côté de Kepler, debout. Il s'agit de Jöst Bürgi (1552-1632), technicien remarquable ès horlogerie, Suisse comme il se doit... Il est d'une grande aide pour Kepler dans la fabrication de nouvelles lunettes, il est aussi un mathématicien d'une réelle compétence -il a inventé avant Néper son propre système de logarithmes! Outre des horloges très précises, il a réalisé de magnifiques globes célestes (certains mécanisés), d'où la représentation choisie par le sculpteur. Des quatre personnages représentés sur le socle à Weil, il est donc le seul à ne pas être un prédécesseur, un maître pour Kepler, mais plutôtun compagnon de travail.

Le livre suivant ne paraîtra qu'en 1609: après 8 ans d'une lutte acharnée contre Mars, il percera définitivement le mystère et révolutionnera la mécanique céleste: adieu les cercles, symboles d'une supposée perfection divine, place à l'ellipse! Trop longue pour être racontée ici, cette aventure mérite bien une page à elle toute seule, vous la trouverez prochainement ici. Contentons nous en cette place, pour ne pas casser le rythme de notre biographie, de l'évoquer par quelques unes de ses magnifiques images

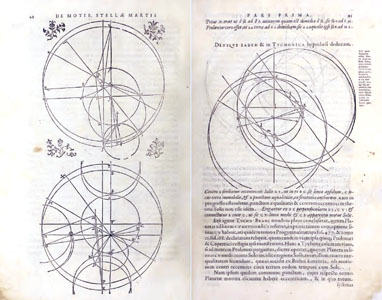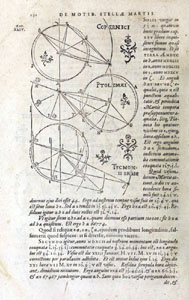
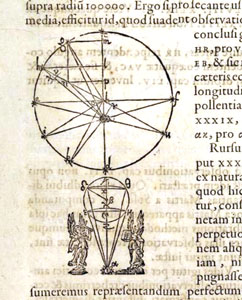
page de titre de l'Astronomia Nova	Comparaison: Systèmes de Copernic, Ptolémée, Tycho	figure et calculs...	l'Astronomia Nova est en ligne sur le site  Internet Archive

Des images qui ont leur beauté propre, même pour celui  à qui la signification géométrique échappe (laquelle ne peut être comprise que par une étude approfondie du contexte).  La meilleure preuve  est sa capacité suggestive pour l'artiste chargé de réaliser un timbre  commémorant en Allemagne fédérale  le 400ème anniversaire de la naissance de Kepler. Plus d'une cinquantaine de timbres rendent, de part le monde, hommage à Kepler; ils sont à découvrir sur le très complet site de Jeff Miller (auquel nous avons emprunté celui-ci)

 
C'est cet épisode  que narre le dernier relief du socle à Weil der Stadt: Kepler, assis, montre un rouleau (un manuscrit?) sur lequel le titre Astronomia Nova est bien en évidence. Face à lui, bras croisés, l'empereur Rodolphe II, dédicataire; tandis qu'à gauche, les imprimeurs s'activent en vue d'une diffusion massive de l'ouvrage qui va révolutionner l'astronomie. Allégorie plutôt qu'anachronisme, derrière lui, dévoilant une sphère armillaire, se tient son "guide" Tycho Brahé, reconnaissable à ses longues moustaches. Ou est-ce un fantôme? On en a déjà vu, au Royaume du Danemark...

"Kepler trompé comme lui, par l’opinion que leurs mouvemens devaient être circulaires et uniformes, essaya longtemps de représenter ceux de Mars, dans cette hypothèse. Enfin, après un grand nombre de tentatives qu’il a rapportées en détail dans son ouvrage De Stella Martis, il franchit l’obstacle que lui opposait une erreur accréditée par le suffrage de tous les siècles: il reconnut que l’orbe de Mars est une ellipse dont le soleil occupe un des foyers, et que la planète s’y meut de manière que le rayon veçteur mené de son centre à celui du soleil , décrit des aires proportionnelles au temps . Kepler étendit ces résultats à toutes les planètes, et il publia en 1626, d’après cette théorie, les Tables Rudolpbines à jamais mémorables en Astronomie, comme ayant été les premières, fondées sur les véritables lois du système du monde, et débarrassées de tous les cercles qui surchargeaient les tables antérieures. Si l’on sépare des recherches astronomiques de Kepler, les idées chimériques dont il les a souvent accompagnées, on voit qu’il parvint à ces lois de la manière suivante." P.-S. de Laplace, Précis de l'Histoire de l'Astronomie

Le timbre (site de Jeff Miller) évoque, un peu discrètement, la loi des aires  les deux triangles mixtilignes de la figure, dont le sommet commun est le Soleil (au foyer de l'ellipse), ont la même aire; la planète (le petit disque noir sur l'ellipse) doit donc, dans un même temps, parcourir une plus grande distance lorsqu'elle est proche de son périhélie (à gauche) -donc avoir une plus grande vitesse; au contraire, c'est au voisinage de l'aphélie (point le plus éloigné de l'orbite, à droite) qu'elle est la plus lente. Cela peut surprendre, mais cette deuxième loi, Kepler la découvrit... avant la première (celle qu'on énonce comme telle de nos jours, c'est à dire le mouvement plan sur une ellipse). Nous y reviendrons dans notre page dédiée.

N'oublions pas, avant de quitter Prague, de visiter sa maison (du moins, celle qu'il occupa de 1607 à 1612), devenue, comme celle de Weil, un musée.

Porche d'entrée...  Karlova str. No 4	Sous le porche	Dans la cour, la fontaine
On n'y trouvera pas de pièces originales, pas de beaux livres anciens, en particulier... C'est un peu dommage; mais les panneaux explicatifs - du même genre qu'à Weil- sont clairs, en deux langues (tchèque/anglais), et l'accueil est sympathique. Ou faut-il dire était? Au moment d'inscrire le lien vers le musée (il y a aussi une petite page Wikipedia), le Mathouriste découvre qu'il indique un transfert vers le réputé  Musée National des Techniques de la ville... N'est-ce pas un peu dommage? Bien sûr, il a une collection d'instruments astronomiques, mais, vue l'importance du travail de Kepler à Prague, la solution antérieure nous semblait plus judicieuse; on peut craindre que des considérations économiques aient prévalu. Il n'aura donc été ici que 8 ans, de 2009 à 2017... triste ironie, la durée qui avait été nécessaire à Kepler pour triompher de Mars!
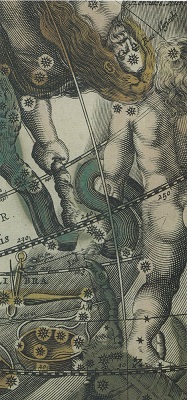
		le ticket d'entrée est très original: évoquant la grande horloge astronomique, il vous délivre l'heure exacte légale, mais aussi sidérale, bohémienne.... de votre venue. Sans compter les positions zodiacales de la lune et de soleil. Un seul conseil: aggrandissez pour le voir!

À Linz

" Matthias entra dans Prague, mais n'y resta que le temps de faire signer à son aîné un acte d'abdication de ses ultimes titres, excepté celui dempereur dont ni l'un, ni lautre ne disposaient. Puis il repartit à Vienne, ne laissant à son frère que la couronne de Charles Quint et son château. [...] Hors de l'enceinte du quartier du château, rien ne changea. Partout en ville, la mort continuait de frapper. Comme toujours et partout, outre le fer, le feu, l'eau et la corde, la soldatesque avait apporté la peste et le typhus avec elle. Cette épidémie -là, on l'appela «la fièvre hongroise». Les hauts murs cernant le Hradschin n'auraient pu interdire l'accès à ses miasmes putrides. " J.-P. Luminet, L'Œil de Galilée

Avec le déclin, puis  la mort en 1612 de Rodolphe II , auquel succède son frère Matthias, une période troublée s'installe à Prague; tout en restant Astronome Impérial, Kepler accepte de s'éloigner et part pour Linz, où il demeurera jusqu'en 1626: ce sera la ville où il aura le plus longtemps séjourné. Sa dernière maison est très facile à trouver: depuis l'immense Hauptplatz centrale, on s'engage dans l'étroite  Rathausgasse jusqu'au numéro 5 , où deux plaques rappellent qu'il y séjourna.   

Hauptplatz; l'ancien hôtel de ville est le bâtiment avec une tour. La Rathausgasse est la ruelle à gauche du bâtiment.	La Rathausgasse (soit, rue de l'hôtel de ville!)	Maison de Kepler au n°5

La plus récente des deux plaques est aussi la plus précise: Kepler a habité ici de 1621 à 1626; c'est son dernier domicile à Linz. Et avant? Si la rue était connue (Hofgasse), l'emplacement exact demeurait un mystère, percé en 2018 par un ingénieur et astronome amateur, Erich Meyer. En exploitant plusieurs documents, et l'impossibilité d'observer de chez lui une éclipse de lune, obstruée par une tour, il a réussi à établir que seul le n°7 convenait! la maison du 7, Hofgasse

à lire sur cette révélation récente: l'article de Ciel des Hommes (traduit de celui de la Nasa) et l'article très détaillé d'Erich Meyer.

Qu'a fait Kepler à Linz?

Lorsqu'il y vient, les Tables Rudolphines sont loin d'être achevées; elles occuperont même toute sa période de Linz, et leur parution, en 1626 à Ulm,  sera postérieure à son départ de cette ville. Mais loin de la simple, voire fastidieuse compilation d'observations -si précieuses fussent-elles-  et de calculs répétitifs de positions intermédiaires,  il lui reste à parachever sa théorie: l'Astronomia Nova ne contenait que ses deux premières lois. La troisième ("Le carré de la période est proportionnel au cube du demi-grand axe"), il la conçoit en 1618 à Linz, et fait paraître dans cette ville son traité définitif en 1619: il s'appellera L'Harmonie du Monde, Harmonices Mundi (disponible en ligne sur Internet Archive).

Cet ouvrage est autre chose, et beaucoup plus qu'un "simple" traité d'astronomie. Il suffit de regarder sa division en 5 livres pour s'en convaincre: rien de ce qui touche à des proportions harmonieuses ne doit y échapper: géométrie évidemment, mais tout autant architecture, musique, et, le plus étonnant au livre IV:  métaphysique (!), psychologie (!!) et astrologie (!!!) Cela démarre sans surprise au degré zéro: qu'est-ce qu'une figure réulière? Suibvent les polygones...  Quand enfin on parvient au livre V, on se dit, que, cette fois, il va (enfoin) être question de lespace et des planètes...

Certes, mais il commence... par les polyèdres réguliers. Autrement dit: il n'a pas renoncé aux idées du Mysterium Cosmographicum! Et, entre ce chapitre I, et le chapitre VI, où il se préoccupe de faire correspondre à chaque planète une musique, quelque part dans le bas d'une page du chapitre III... elle est là, la troisième loi de Kepler! Comme un défi pour archéologue...

Traduction: "Mais s'il est une chose la plus certaine et la plus exacte, c'est que la proportion qui existe entre les périodes de deux planètes est précisément une fois et demi comme le rapport de leurs distances moyennes [au Soleil]" Autrement dit: T1 /  T2  = k ( R1 /  R2  ) 3 / 2 car le préfixe sesqui signifie: "une fois et demi" (les mathématiciens l'emploient encore, notamment dans l'expression forme sesquilinéaire ). Le "raayon moyen" peut sans inconvénientêtre remplacé par le demi grand axe pour une orbite elliptique.

Après quoi, notre astronome revient à ses obsessions de correpsondances musicales, cette fois avec les intervalles de la gamme. C'est dans le rapport des vitesses au périhélie ou à l'aphélie de chaque planète qu'il pense trouver la simplicité cherchée. Les planètes sont représentées par leurs symboles usuels; on trouve, de haut en bas (et dans l'ordre décroissant de l'éloignement au Soleil) Saturne (pour qui le rapport en celui de la tierce majeure), Jupiter (tierce mineure), Mars (quinte)  , Terre (demi-ton), Vénus (demi-yton chromatique), Mercure (octave + tierce mineure). [ sur la correspondance entre intervalles musicaux et rapports, voir notre page sur l'harmonie et l'analyse de Fourier] Le tableau contient en fait des mesures angulaires, correspondant à l'arc parcouru en un jour au voisinage du sommet considéré.

Il rédige aussi à Linz une défense et synthèse de l'astronomie copernicienne telle qu'il l'a adaptée avec ses mouvements elliptiques, l'Epitomes astronomiae copernicanae . Elle paraît en 1618 et recèle un nouveau joyau, sa réinvention de la Méthode des Approximations successives, afin de donner les éphémérides de Mars qui seront inclus dans les Tables Rudolphines. Réinvention, parce que le procédé a déjà eu un inventeur de génie, Al-Kashi, ami et collaborateur d'Ulugh Beg à l'Observatoire de Samarcande (les liens pointent vers nos pages dédiées). Il est plus qu'imporbable que Kepler ait eu connaissance de ses travaux, de deux siècles antérieurs (vers 1420-1430), mais fort éloignés dans l'espace. L'histoire des sciences fourmille de découvertes multiples, indépendantes... toujours par des génies de premier ordre! Mais de tout cela, nous reparlerons dans la page dédiée à la traque de Mars, qui en est ele cadre naturel.

Source de l'image: Wikimedia Commons

I

Grande productivité, en dépit de l'environnement d'une période abominable, tant au plan général que dans sa vie familiale.
En 1618 éclate en effet la Guerre de 30 ans, la première "véritable" guerre européenne, qui ravage tout le Saint Empire Romain Germanique sur fond d'antagonisme religieux exarcerbé. Tout a commencé (du moins, l'étincelle s'est allumée) ici, au château de Prague, par la célèbre défénestration de deux collecteurs d'impôts de l'empreur autrichien.

Prague: le célèbre château, et sa non moins célèbre fenêtre

Qui, mieux que Brecht, peut traduire l'ambiance des années qui vont suivre? (Même si c'est pour lui, avant tout, à la fois une métaphore de ce qui guette à nouveau l'Europe et l'expression intemporelle des réalités passées, présentes et à venir))

Voir cette scène, dirigée par Jean Vilar (1958) (extrait, archives de l'INA)	" LE SECRÉTAIRE - Et la paix, qu’est-ce que vous en faites de la paix? Moi je suis de Bohème et je voudrais bien rentrer chez moi.   L'AUMÔNIER - Rentrer chez vous, la paix... Que reste-t-il du trou après avoir mangé le fromage ? Mais oui, d’une façon ou d’une autre la guerre s’en sort toujours. Pourquoi voulez-vous qu’elle finisse? [...]   L'AUMÔNIER - Souvent je vous admire, à vous voir comme cela, de mener votre commerce et vous tirer toujours d’affaire, je comprends qu’on vous appelle Courage !  MÈRE COURAGE - Faut du courage aux pauvres gens, sans quoi ils sont fichus. Rien que se lever le matin, labourer un champ en temps de guerre, ou mettre au monde des enfants quand l’avenir est sans espoir, ça suppose un sacré courage. Vous pourriez fendre un peu de bois !   L'AUMÔNIER - Je suis pêcheur d’âme, Courage, je ne suis pas bûcheron !   MÈRE COURAGE - Et moi je n’ai pas d’âmes à prêcher, j’ai du bois à couper Tout ce que je cherche c’est à nous tirer d’affaire au mieux, moi, mes enfants et la roulotte. J’ai pas le coeur à la romance. En ce moment je cours un gros risque en achetant du matériel. Le maréchal d’Empire est mort et tout le monde parle de paix. Que deviendriez-vous, si je perdais tout mon bien, hah, ben vous voyez, vous n’en savez rien. Alors fendez-nous du bois, on aura chaud le soir, et par le temps qui court, c’est pas si mal." Bertolt Brecht, Mère Courage et ses enfants (1938) inspiré  de H. Grimmelshausen, les Aventures de Simplicius Simplicissimus (1669)
N.B. sur la pièce de Brecht, l'article Wikipedia en Allemand est bien plus complet que celui en Français (donc conseillé à ceux à qui connaissent un peu la langue). On trouvera le synopsis suivi d'une analyse ici, une  autre analyse là,

À l'inquiétude des temps s'ajoute, pour Kepler, un autre souci: sa mère est accusée de sorcellerie à Leonberg. Le voyage est risqué, mais il n'hésitera pas à s'y rendre et assurer lui-même sa défense. Sa plaidoirie est conservée dans ses Opera Omnia; il obtient l'acquittement! C'est le sujet de l'opéra de Tim Watts Kepler's Trial (2009)

À Regensburg (Ratisbonne), la Fin du Voyage ...

" Le retour des moines et des prêtres catholiques à Linz avait mis le feu aux poudres à toute la Haute Autriche. On redoutait en effet qu'avec l'Église romaine revienent également dîme, taxes, indulgences, interdiction de pratiquer librement son culte, bûcher, torture et Inquisition. À quoi s'ajoutait l'occupation de la capitale par les Bavarois, ennemis héréditaires des Autrichiens. [...] Ce fut bel et grand massacre sur les deux rives du Danube. Pris en tenaille, les restes de l'armée paysanne n'eurent d'autre resource que de se réfugier dans Linz et tenter d'y résister le plus longtemps possible. Ils défoncèrent les portes de la ville et pénétrèrent dans la cité en hurlant leur désespérance, jetant des torches allumées dans les premières maisons qu'ils avaient réussi à atteindre. La cavalerie bavaroise, qui était dans leur dos, les sabra jusqu'au dernier. Parmi les quelques maisons brûlées, il y eut l'imprimerie de Kepler. Seul le papier vierge, manuscrit ou imprimé fut épargné par les flammes, vite roulé dehors dans ses tonneaux. Mais la presse et l'horloge à calculer étaient parties en fumée, et les caractères destinés aux Tables Rudolphines transformées en une marre de plomb fondu. La pais revint en Haute Autriche. [...] La situation à Linz devenait intenable. [...] Le mathematicus impérial n'avait donc plus rien à y faire. Il proposa Nuremberg ou Ratisbonne comme nouvelle résidence possible, espérant que, en croyant lui nuire,  l'empereur l'enverrait à Franfort. Ce fut Ratisbonne." J.-P. Luminet, L'Œil de Galilée

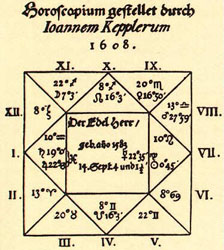(Source: Wikimedia Commons)

En fait, ces quatre dernières années de sa vie tiennent plutôt d'une errance entre Ratisbonne, Ulm -où il réussira à faire enfin imprimer les fameuses Tables Rudolphines- et  Sagan, chez son dernier protecteur, le  duc de Wallenstein, façon pour ce dernier de le remercier, bien des années après, du radieux horoscope que Kepler lui avait dressé en 1608. Chance pour l'astronome, les prédictions de l'astrologue ne s'étaient pas trop mal accordées à la réalité... Quant aux Tables, Kepler fut moins heureux: tirées à 1000 exemplaires, elle s ne suscitèrent guère d'enthousiasme, notamment à la Foire de Francfort(!), pour laquelle Johannes avait de plus grandes espérances. Il devait noter: "Il y a peu d'acheteurs: c'est toujours le cas des ouvrages mathématiques, particulièrement en ces temps de chaos." La situation a-t-elle beaucoup changé, 4 siècles plus tard ? Tables Rudolphines: pages de titre et début de la table de la Lune (Source: Internet Archive)

La gravure de la page de gauche est une allégorie, celle d'un temple à l'Astronomie (tout ce qu'il y a de plus imaginaire). Sur les quatre colonnes à l'avant, on distingue, de gauche à droite, les noms  d'Hipparque, Copernic, Tycho Brahé et Ptolémée; chaque astronome se tient près de sa colonne avec un signe de reconnaissance: un grand quadrant pour Tycho, une tablette faisant apparaître le point équant, dont on pense qu'il est l'inventeur. Notez qu'en fin géomètre, Kepler a choisi pour base de son temple un décagone, ce qui est particulièrement rare dans la réalité! .

À peine installé de façon un peu plus définitive à Ratisbonne, Kepler décède. Sa maison est, ici aussi, devenu un musée... que le Mathouriste n'a pas encore eu l'occasion de visiter. En ces temps de chaos (2020-21), les projets touristiques sont fortement contrariés!

Source: page Maison de Kepler dans Wikipedia

Kepler fut inhumé au cimetière de Regensburg, ravagé lors de la guerre de 30 ans: sa sépulture  n'a pas été  retrouvée. « Voilà seize ans que dure la grande guerre de religion. L’Allemagne y a perdu plus de la moitié de ses habitants. De gigantesques épidémies tuent ce que les carnages ont épargné. La faim sévit dans les régions jadis florissantes. Des loups rôdent dans les villes réduites en cendres. » Bertolt Brecht, Mère Courage et ses enfants , présentation liminaire duTableau 9
Toutefois  un monument commémoratif, quelque peu néo-classique (rappelant le temple imaginé en frontispice des Tables Rudolphines), a été édifié. Inauguré en 1808, endommagè en 1809 lors de la bataille (page plus complète en Allemand) ayant opposé les troupes napoléoniennes aux Autrichiens, il a été restauré, et déménagé en 1859 dans la Fürst-Anselm-Allee lors de la construction de la gare ferroviaire.
Source: page Kepler-Monument (Regensburg) dans Wikipedia... en attendant de faire une visite sur place.

Références

Œuvres

• Opera Omnia, sur le site e-rara de l'ETH Zürich (des volumes séparés de certains ouvrages sont aussi disponibles)
• Mysterium Cosmographicum (sur le site e-rara )
• Astronomia Nova (sur le site  Internet Archive )
• Harmonices Mundi ( sur le site  Internet Archive )
• Tables Rudolphines  ( sur le site  Internet Archive )
• Epitomes astronomiae copernicanae   ( sur le site  Internet Archive )

Livres:

• M. CASPAR, Kepler (Dover)
• M. CROWE, Theory of the World from Antiquity to the Copernician Revolution (Dover)
• J.L.E. DREYER, A History of Astronomy from Thales to Kepler (Dover)
• A. KOYRÉ, The Astronomical Revolution: Copernicus, Kepler, Borelli (Dover)
• J.P. VERDET, Une Histoire de l' Astronomie (Seuil, points Sciences)
• Les Cahiers de Science & Vie , Kepler (Les Pères Fondateurs de la Science, Hors Série n°21, juin 1994)
• Pour la Science , Kepler, le Musicien du Ciel (Les Génies de la Science, Hors Série n°8, août 2001)

Articles ou livres en ligne  

• W. BRYANT, Kepler (Collection Men of Science)
• J. HASNER, Tycho Brahe und Kepler in Prag, Eine Studie (Google Books)
  
• J.P. VERDET, La Diffusion de l'Héliocentrisme sur le site Persée.

Films:

• L'œil de l'astronome - Film  de Stan Neumann, avec Denis Lavant (2012)
  

Operas:

• Die Harmonie der Welt, opéra de Paul Hindemith (1957; symphonie éponyme, 1951)
• Kepler, opéra de Philip Glass (2009)
• Kepler's Trial, opéra de Tim Watts (2009), livret de l'historienne U. Rublack (Cambridge) et sur le site du compositeur.
  

 

Sites:

• Société Kepler: Kepler Gesellschaft

Poursuivre dans nos Pages...

• Tout particulièrement nos pages Copernic son De Revolutionibus
  

Revenir à la  Home Page du Mathouriste