Lorenzo Mascheroni: son buste à Bergame
 |
 |
| la ville basse, vue de la ville haute | dans la ville basse (Porta Nueva), vue sur la ville haute |
|
 |
|
| Le monument se trouve à l'extrémité de la flèche jaune;
noté M comme... Mascheroni. (Cliquez pour aggrandir!) Car un autre
protagoniste de l'histoire ne va pas tarder à apparaître, en rouge, un
certain B... |
|
Son plus grand titre de gloire est la publication en 1797 de sa Géométrie du Compas,
ouvrage dans lequel il démontre que tout point constructible à la règle
et au compas (selon le canon de la géométrie grecque, qui allait faire
naître avec cette exigence un foisonnement de problèmes -voir notre page Délos) l'est aussi à l'aide du seul compas. Autrement dit... la règle est inutile!
C'est un succès immédiat;
en témoigne le fait que le livre est aussitôt traduit en Français. On
ne découvrira que bien après que le Danois Mohr (1640-1697) avait
obtenu, avant lui (1672), les mêmes résultats, mais on ne saurait
accuser l'Italien de plagiat: ce premier travail avait été bien peu
diffusé: le livre de Mohr, Euclides Danicus,
ne fut redécouvert qu'en 1928, presque par hasard, par un compatriote
mathématicien, Hjelmslev. Le titre suggérait un simple commentaire
d'Euclide, il fut surpris d'y lire les résultats deMascheroni, mais
souvent démontrés d'une manière différente: lItalien s'était posé
la même question, tout simplement, et
il était parvenu, en totale indépendance, au même résultat.
Mais... à qui donc fut dédié ce livre? |
 source: e-rara (ETH Zürich)
|  |
||
 |
 |
 |
 | |
| Eh bien oui! Celui qui vient de s'illustrer militairement dans la région, entre 1796 et 1797, et dont une colonne rappelle justement à Bergame qu'il
fut, au moins ici et pour un certain temps, perçu comme un
libérateur... De fait, les populations locales se trouvaient ainsi
débarassées des Autrichiens, sans être forcément enthousiastes à l'idée
de voir les Français les remplacer. Érigée en 1797, exactement
contemporaine du traité de Mascheroni, elle porte (vous le verrez en
l'aggrandissant) la même dédicace "à Bonaparte l'Italien" et se trouve
à proximité: c'est elle que nous avons indiqué par la flèche rouge sur la vue aérienne! |
||||
Ci-contre: faire glorifier ses batailles victorieuses par les peintres... ... et ci-dessous, se
faire immortaliser en séduisant jeune premier, empoignant le
drapeau pour entraîner à sa suite une troupe hésitante sur le pont
d'Arcole, au mépris de la mitraille ennemie! Hollywood aurait eu du mal
à faire mieux, et d'ailleurs l'avisé général adopte avec avance la
morale de L'homme qui tua Liberty Valence:
"Quand la légende est plus belle que l'Histoire, on imprime la légende!" (l'image fut massivement diffusée en gravure) |
 bataille du pont de Lodi, 10/05/1796
|
 bataille de Rivoli, 13-140/01/1797
|
|
 |
 Gros, 1796 (Musée de Versailles) à l'exposition de la Villette-2021 |
Mais... si
Gros flatte le vainqueur par l'image (les historiens ont révélé qu'il
avait dû reculer si vite qu'il était tombé dans un marécage!),
Mascheroni n'était pas en reste dans sa
dédicace, et le traducteur n'a pas hésité à en remettre une couche, ou
plutôt quelques vers dithyrambiques!
Le stratège fit mieux: à son retour à Paris, tout en présentant fièrement l'édition italienne, il s'attribua le mérite -inspiré par l'ouvrage- de ce que l'on appelle depuis la construction de Napoléon: retrouver à l'aide du seul compas, le centre -supposé perdu- d'un cercle donné. (Les plus mathématiciens des lecteurs pourront s'intéresser à une justification par l'inversion, transformation géométrique qui transforme les droites en cercles) L'auditoire était choisi, y figuraient notamment Lagrange et Laplace. Ce dernier, jamais en retard d'une flatterie, s'écria, nous rapporte Lebesgue: "Nous attendions tout de vous, Général, sauf des leçons de Géométrie!"
La manœuvre réussit: avec ce bien mince bagage de "chercheur-découvreur" et le puissant soutien de Monge -qui l'avait suivi dans la campagne d'Italie-, il fut élu à l'Académie des Sciences. Et, honte suprême, au fauteuil de Carnot,
alors banni, mais bien plus mathématicien que lui. Certes, c'était sa
matière forte, et il est incontestable qu'il avait du goût pour elle...
mais essayez donc, avec du goût, de bons résultats scolaires et une
bricole, d'entrer dans cette vénérable institution! En tout cas, cela
lui permettra de signer ses courriers, lors de l'expédition d'Égypte, le membre de l'Institut, Commandant en chef de l'Armée d'Orient... |
|
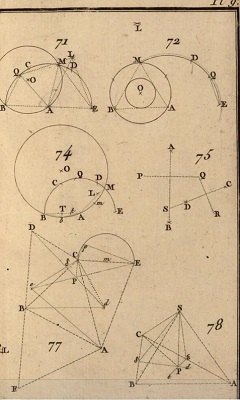
La solution de Mascheroni dans son livre: (vous n'êtes pas obligé d'en suivre les détails!) |
|||
 |
 |
 |
|
 |
C'est probablement dans cette ville que Mascheroni rencontra Bonaparte, car c'était sa résidence à l'époque de la campagne d'Italie. C'est là qu'il fit toute sa carrière universitaire, puis politique, car il devint député de la République Cisalpine, établie par Bonaparte. De quoi être honoré par une rue, à double titre. Il fut à ce titre envoyé à Paris, pour participer à la commission de définition du mètre. Mais il ne revint jamais, en raison de la formation de la deuxième coalition, qui vit le général repartir pour une deuxième campagne d'Italie; il décéda à Paris en 1800... le 14 Juillet. |
| rue Mascheroni à Pavie |
 |
 |
 |
Sitôt passée l'entrée, l'université de Pavie offre à notre vue une agréable succession de belles cours carrées, bordées d'arcades. Et sous l'une d'elles... une plaque apposée (en 1808) en souvenir de celui qui y enseigna l'algèbre et la géométrie à partir de 1786. Il en fut même le recteur de 1789 à 1793! i |
 |
 |
 |
Le plus illustre de ses élèves fut le physicien Alessandro Volta (1745-1827), inventeur de la pile électrique en 1800... et qui, lui aussi, rencontra Bonaparte en 1801, pour lui présenter son invention! Pour son cas, la rencontre eut lieu à Paris, à la suite d'une très officielle invitation. |
 |
 |
|
statue de Volta
à l'université de Pavie
|
Volta fait à Bonaparte la démonstration de sa pile électrique Fresque de Nicolo Cianfanelli (1841) Tribune de Galilée, Musée "La Specola", Florence |
 |
Mais puisque Mascheroni était aussi poète, on trouvera au mur d'une autre cour, une de ses œuvres... |
Dansle livre de Mascheroni: |
||
 |
 |
 |
| l'ouvrage (à voir en entier sur Google Books) |
début de l'article |
le passage où il donne la nouvelle valeur |
|
À tout seigneur, tout honneur!
L. MASCHERONI, Géométrie du Compas (éd. française), sur Google BooksOn remarquera que
l'auteur, même si son objet premier est de donner des constructions
géométriques exactes, ne dédaigne pas s'intéresser également aux
constructions approchées, utiles dans tous les problèmes pratiques que
peuvent rencontrer les artisans; c'est l'objet de son dernier chapitre. La précision de chaque approximation est clairement indiquée.
|
|