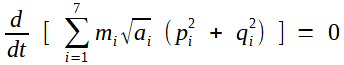LAPLACE, du Pays d'Auge à la gloire parisienne
Le
Mathouriste commencera par remercier celle qui, voici pas mal d'années, a
pensé à lui expédier cette carte postale (
garantie "recolorisée" d'origine! ) depuis le petit village du
Calvados où est né l'auteur de la Mécanique
Céleste.

Voilà
qui donne envie d'aller y voir soi-même, non? Une pause bien
sympathique sur la route vers la Bretagne!
Né à Beaumont en Auge
C'est un petit village, typique du bocage normand; comme son nom
le suggère: il est posé au sommet d'une colline, à 90m d'altitude.
Quand on y arrive, on ne voit guère que le clocherqui émerge d'un
environnement verdoyant; et une fois au pied de la statue -très
précisément derrière elle, le regard embrasse un large paysage de
campagne, la vallée de la Tougnes

|

|

|
vue, depuis l'arrière du monument
|
vue, depuis l'arrière de l'église
|

|

|
En comparaison avec la carte postale, on constatera que
lenvironnement a peu changé... en ce qui doit être une bonne
soixantaine d'années, si ce n'est plus. On pourra même jouer au jeu des
sept erreurs... le sol, les plantations au pied du monument, les arbres
enfin (mais ont-ils simplement grandis? N'avaient-il s pas été effacés
au profit d'un ciel de convenance à la gloire de celui qui en avait
maîrtisé les secrets? Car le projet précisait bien:
"Un rideau de verdure, en forme d'hémicycle,constituera un fond naturel qui le mettra bien en valeur."
Mais les arbres meurent aussi... Quoi qu'il en soit, les petits
villages ont cet avantage sur les grandes villes: ils changent moins
vite d'aspect, ce qui peut s'avérer avantageux lorsqu'on cherche les
traces du passé.
|
Ce monument n'a été érigé que plus d'un siècle après le décès de
Laplace. C'est, comme hélas souvent, moins le défaut d'intention que...
de financements, et sans l'impulsion de généreux mécènes, les villes
départements, régions -pour ne rien dire de l'État- rechignent à
prendre l'initiative: suivre, volontiers, aider, faciliter, d'accord;
épauler financièrement, c'est envisageable, mais sans prendre la tête
de l'opération, sans doute par crainte du contribuable, qui se trouve
aussi être un électeur... rien de bien nouveau, voici de quoi en juger:
"L'idée
d'un monument à Laplace en son pays natal de Beaumont en Auge ne date
pas d'aujourd'hui. Cette initiative avait été prise par M. Guilbert, de
Pont-l'Évêque, membre de la Société Astronomique, encouragée et
soutenue par la municipalité d'alors [...]. Pour mener à bien cette
délicate entreprise le Comité savait à quelles difficultés matérielles
il se heurterait, aussi avait-il fait appel au concours d'un artiste
normand dont la réputation était bien établie, M. Robert Delandre."
Journal Le Pays d'Auge, 01/08/1931
|
En effet, Robert Delandre
(1869-1961) est un sculpteur reconnu, d'autant qu'il vient de signer en
cette même année, en compagnie de l'architecte Léon Rey, le monument "À ceux du Latham 47", cet hydravion prêté par la France pour porter secours à l'équipage du dirigeable Italia d'Umberto Nobile dans l'Arctique (1928), et disparu avec tout son équipage, dont le vainqueur du Pôle Sud, Roald Amundsen.
"
[...] et grâce à la bienveillante intervention de notre ami, M. de
Navailles, M. Maujendre, consul général de France à New-York, intéressa
certaines personnalités américaines à notre projet, notamment M. John
Flanagan, statuaire, et M. John Fry, peintre, tous deux artistes de
grand mérite qui surent appércier à sa valeur l'œuvre de M. Robert Delandre et nous apporter leur concours le plus précieux."
Journal Le Pays d'Auge, 01/08/1931
| 
|
Voilà qui explique qu'on
ait gravé à droite du socle une pensée de John Hemming Fry, fort
judicieuse d'ailleurs, et de bon conseil pour la France en général, qui
a tendance à abuser des statues de militaires, alors que bien des
personnalités civiles mériteraient d'être honorés dans l'espace public
sur la base de leur reconnaissance internationale.
|
Symétriquement, du côté gauche,
on trouve la liste des bienfaiteurs, dont l'Institut
Carnegie pour la paix et la science, qui a fourni une
contribution importante. Les médaillons sont ceux de Galilée (face
gauche du socle) et Newton (face droite du socle): voilà donc Laplace à son tour "juché sur les épaules des géants" comme l'illustre auteur de cette formule (1676, lettre de Newton à Robert Hooke,
avant de devenir le titre d'un livre de Stephen Hawking démontrant
l'universalité de ce principe cmulatif en science). Mais au fait, où
est passé Copernic? Il aurait amplement mérité sa place, d'autant que
la face arrière est vierge. D'ailleurs, le trio de prédécesseurs de
Laplace serait plutôt Copernic-Képler-Newton, mais ne chipotons pas, et respectons le choix des concepteurs.
C'est donc sans ambiguïté l'auteur de la Mécanique
Céleste que l'on honore, et les détails de la "mise en scène" du héros vont, bie entendu, souligner cet aspect essentiel de son œuvre. Le regard la découvre en balayant naturellement, de haut en bas:

|

|
- la première chose qu'on voit, c'est un Laplace pensif, concentré: c'est le geste, ou plutôt la pause, de sa main droite;
- suivons alors son bras gauche: nous découvrons , dans sa main, un compas, symbole de son activité de mathématicien;
- mais cette main est posée sur un globe: ce déploiement mathématique est là pour servir la cause de l'astronomie...
|
- ... et ce globe, c'est Atlas qui le soutient, comme dans la légende grecque! Il est vrai que remettre de l'ordre dans le Système du Monde
était un travail herculéen; en auriez-vous douté, la composition vous
le rappelle. D'une certaine façon, dans cette allégorie, c'est le monde
entier que Laplace maîtrise de sa main.
|
 |

|
L'inauguration eut lieu le 3 juillet 1932, et le même journal la relate. On croirait le récit sorti du Petit Nicolas de Sempé et Goscinny, fins observateurs, il est vrai, de leur époque avant de confier leurs impressions à la plume enfantine...
"Les
autorités furent reçues à la mairie, où le maire, M. Biatarana, entouré
de son conseil municipal, leur souhaita la bienvenue. En cortège,
précédé de la musique de Pont-l'Évêque et des drapeaux des anciiens
combattants, escortés par les sapeurs pompiers et les enfants des
écoles, les autorités se dirigèrent vers la place où est élevé le
monument à Laplace. Ce monument, ainsi que nous l'avons dit, est situé
non loin de la maison où naquit l'illustre astronome, aujourd'hui transformée en musée. Une estrade avait été élevée, où prirent place les autorités."
Journal Le Pays d'Auge, 04/07/1932
|
Elle est même tout près, cette maison: de l'autre côté de la place
de Verdun, faisant l'angle avec la rue... Pierre Simon Laplace, bien
sûr! Le grand savant peut la contempler tout en s'adonnant à sa céleste
méditation. C'était en fait, à sa naissance, un bâtiment plus modeste,
l'Hostellerie de la Sainte-Croix, qui fut acquise par la mairie en 1834 pour y loger l'école primaire.

|
Cette
école primaire, elle est toujours là, comme en témoigne la pancarte
tricolore surmontée de drapeaux, dans cet ajout peu grâcieux à droite
de l'immeuble.
Et quid du musée évoqué par le journal, direz vous? Rien d'ouvert, rien à voir lors du passage du Mathouriste
; atil existé, puis a été fermé? Y a-t-il quelques objets souvenirs qui
dorment dans des caves ou greniers, faute de moyens en matériel et en
personnel pour maintenir ouvert un lieu d'exposition? Toujours est-il
qu'existe une Société des Amis de Laplace, qui annonce sur son site web
vouloir faire de ce lieu un musée: l'idée n'est donc pas morte!
Souhaitons leur de réussir...
|
Au fronton fut rapporté en 1835, à l'initiative du maire, une plaque de marbre gravée de deux inscriptions:
- à droite la dédicace de la ville et du département;
- à gauche quelques vers de l'inspecteur d'académie et poète
Charles-Julien Lioult de Chênollé; comme le sculpteur, il célèbre avant
tout le Newton Français, celui qui sut "de Newton aggrandir le compas."
Un compas, il y en a un dans le blason central, en compagnie d'autres
objets indispensables de la trouse du mathématicien en campagne:
équerre, rapporteur, sphère...
|

| 
|
Aggrandissez par clic pour lire plus facilement les deux textes.
|
Il fut tout naturellement baptisé dans l'église du village,
Saint-Sauveur, deux jours après sa naissance, soit le 25 mars 1749.
Rappelons qu'autrefois, l'usage était de baptiser les enfants au plus
vite, en raison d'une mortalité périnatale très élevée.
Pour ses études, le jeune Pierre-Simon a de la chance:
l'ancien Prieuré Notre-Dame, tranformé en Collège Royal,
est là, tout proche, à un jet de pierre de sa maison (comme on peut le voir ci-dessous). On y
prépare l'accès aux Écoles Militaires, et l'enseignement y est de
bonne qualité, tout en faisant une place importante à l'éducation
religieuse.
À nous deux, Paris!
Des débuts remarqués

peint par Catherine Lusurier en 1877
Musée Carnavalet, Paris
|
"Il
se présenta chez d'Alembert, précédé de recommandations nombreuses,
qu'on aurait pu croire très puissantes. Mais ses tentatives furent
inutiles: il ne fut même pas introduit. C'est alors qu'il adressa à
celui dont il venait de solliciter le suffrage une lettre fort
remarquable sur les principes généraux de la mécanique, et dont M.
Laplace m'a, plusieurs fois, cité divers fragments. Il était
impossible qu'un aussi grand géomètre que d'Alembert ne fût point
frappé de la profondeur singulière de cet écrit. Le jour même, il
appela l'auteur de la lettre, et lui dit, ce sont ses propres paroles:
« Monsieur, vous voyez que je fais assez peu de cas des recommandations; vous n'en aviez pas besoin. Vous vous êtes fait mieux connaître; cela me suffit: mon appui vous est dû.» Il obtint, peu de jours après, que Laplace fût nommé professeur de mathématiques à l'École Militaire de Paris."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|

|

|

|
Oui, au moment où Laplace entre comme enseignant à l'École Militaire, en 1769,
le bâtiment dessiné par Ange-Jacques Gabriel, entrepris dès 1751, est
toujours en chantier. Mais il sera terminé (1780) quand Laplace y
examinera un petit jeune d'avenir, qui s'y perfectionne en 1784-1785...
 |

| 
| 
|
|
Louis Rochet, Napoléon à Brienne, 1857 (expositions à Arras & Paris, La Villette)
|
Quel livre tient-il en main, ce
jeune homme dont la pose idéalise, dans le cocon de sa jeunesse, la
détermination et l'ambition? Le fameux cours de Bézout,
en usage dans les écoles militaires, qu'il domina en 10 mois, dit-on,
alors que cela demandait 3 ans aux autres élèves? (On n'exclura pas
l'hypothèse d'un léger enjolivement de la chronique, pour faire pendant
à celui de la statue; mais il est vrai que cet élève plutôt moyen avait
pour seule matjère forte les mathématiques.). En tout cas, il a lui
aussi, comme Laplace, un globe (étoilé) à son côté... à chaciun sa
manière de devenir le maître de l'Univers!
Ils devaient se revoir en plusieurs occasions, mais une seule fut
vraiment mathématique: le général victorieux en Italie avait ramené,
entre autres, des œuvres d'art, mais en bon stratège, il avait aussi
pillé à Mascheroni la spectaculaire construction, à l'aide du seul
compas, du centre -supposé perdu- d'un cercle. De quoi éblouir à peu de
frais sa compagnie lors du dîner organisé le 11 Décembre 1797 par son
âme damnée ès sciences, Gaspard Monge, pour préparer son élection à
l'Institut avec ce résultat pour tout viatique. L'opération de
communication réussit à merveille (au point que cete construction est
dénommée, en France au moins, construction de Napoléon). Ce qui fit
dire à Laplace, dont le tempérament courtisan sentait probablement
Napoléon percer sous Bonaparte:
" Nous attendions tout de vous, général, sauf des leçons de géométrie!"
Revenons aux débuts de Laplace. Son enseignement (dont nous n'avons hélas pas de traces) lui
laisse, apparemment, assez de temps pour ses recherches; après quelques
publications qui déjà révèlent ses sujets de prédilection: mécanique
céleste, suites récurrentes et probabilités, il soumet à l'Académie le
10/02/1773 un mémoire qui sera son billet d'entrée -comme adjoint, dans
un premier temps- dans l'institution. Il mêle les deux derniers thèmes mathématiques; on notera un point de terminologie: les équations aux différences finies sont qualifiées d'équations différentielles
alors qu'aucune dérivée n'y figure; ce n'est donc pas le sens qu'on
donne aujourd'hui. Les premières apparaissent comme une
sous-catégorie des secondes (cf la taille des caractères dans le
titre).
in extenso dans Oeuvres Complètes, t.6, sur Gallica (BnF)
|

|
C'est un texte fondateur de ce qu'on va dénommer déterminisme laplacien, défini par cette citation célèbre (§.XXV) qui fera évidemment couler beaucoup d'encre lors de la découverte du chaos déterministe...
"
L'état présent du système de la Nature est évidemment une suite de ce
qu'il était au moment précédent, et, si nous concevons une intelligence
qui, pour un instant donné, embrasse tous les rapports des êtres de cet
Univers; elle pourra déterminer pour un temps quelqconque pris dans le
passé ou l'avenir la position respective, les mouvements, et
généralement les affections de tous ces êtres.
L'Astronomie physique, celle de toutes nos connaissances
qui fait le plus d'honneur à l'esprit humain, nous offre une idée,
quoiqu'imparfaite, de ce que serait une semblable intelligence. La simplicité de la loi qui fait mouvoir les corps célestes,
les rapports de leurs masses et de leurs distances, permettent à
l'Analyse de suivre, jusqu'à un certain point, leurs mouvements; et, pour
déterminer l'état du système de ces grands corps dans les siècles
passés ou futurs, il suffit au géomètre que l'observation lui donne
leur position et leur vitesse pour un instant quelconque; [...] "
Mém. cit., in Oeuvres Complètes, t.6, p.144
|
Mathématiquement, c'est irréfutable: la loi d'attraction de Newton fournit les équations différentielles du second ordre (parce que la force qui s'exerce sur un corps est proportionnelle à so accélération, dérivée seconde de sa position), qui ont une solution unique pour une position et une vitesse initiale données en un point.
Ce qui permet de "suivre" les mobiles dans le futur, ce qui est bien
utile pour bâtir des éphémérides... et organiser les vols spatiaux vers
la Lune, Mars... (et plus si affinités), ou de "remonter le temps" pour
vérifier certaines affirmations d'historiens du passé.
Mais attention, déterminé ne veut pas dire calculable explicitement; et
pour puissantes qu'elles soient, les méthodes numériques employées dans
nos ordinateurs ne sont, et ne peuvent être, qu'approchées.
Quelle place, alors, pour le hasard et les probabiliés? Laplace va en
donnner des définitions extrêment pertinentes pour son époque:
" [...]
mais l'ignorance des différentes causes qui concourent à la production
des évènements, et leur complication, jointe à l'imperfection de
l'Analyse, empêchent [l'homme]de prononcer avec la même certitude sur le plus grand nombre des phénomènes; il
y a donc pour lui des choses incertaines, il y en a de plus ou moins
probables. Dans l'impossibilité de les connaître, il a cherché à s'en
dédommager en déterminant leurs différents degrés de vraisemblance, en
sorte que nous devons à la faiblesse
de l'esprit humain une des théories les plus délicates et les plus
ingénieuses des Mathématiques, savoir la science des hasards et des
probabilités.
[...]
Nous regardons une chose comme l'effet du hasard , lorsqu'elle n'offre
à nos yeux rien de régulier, ou qui annonce un dessein, et que nous
ignorons d'ailleurs les causes qui l'ont produite. Le hasard n'a donc aucune réalité en lui-même; ce n'est qu'un terme propre à désigner notre ignorance sur la manière dont les différentes parties d'un phénomène se coordonnent entre elles et avec la Nature.
La notion de probabilité tient à cette ignorance."
Mém. cit., in Oeuvres Complètes, t.6, p.145
|
Ce point de vue tiendra fort longtemps, jusqu'à l'avènement de la
mécanique quantique, qui confèrera une réalité indiscutable au
"hasard"; mais ce n'est pas le lieu de l'aborder ici: ce n'est pas
facile, et, si cela vous dérange, dites vous que vous n'êtes pas le
seul, et en excellente compagnie: Einstein en personne, qui maugréait
que "Dieu ne joue pas aux dés."
La Période Révolutionnaire
Laplace reste plutôt dans une prudente neutralité, et poursuit
comme si de rien n'était son travail, aussi bien d'académicien
que examinateur: on dispose, par exemple, du témoignage, en 1790, de
Marmont, futur maréchal d'Empire:
1790 est aussi l'année où est envisagé la réforme du système des poids et mesures,
pour mettre fin à une épouvantable anarchie: le nombre des variantes
locales dépassait largement celui, pourtant réputé, des spécialités de
fromages... On songea d'abord à imposer à tous les mesures de la
capitale: ce seul fait indiquera à nimporte qui le pays dans lequel se
déroule l'action; on imagine sans peine les réctions provinciales! Il
fallait, pour dénouer la situation, un individu habile, voire quelque
peu retors: Charles Maurice de Talleyrand-Périgord, il est vrai bien coaché par Condorcet, était l'homme de la situation:
|
Talleyrand, par L. Despret
(musée Carnavalet, Paris)
|
" [...] l'ancien
évêque, révolutionnaire occasionnel et chef immuable de la diplomatie
française, avançait une proposition soutenue par les savants, et
surtout par Condorcet. Au lieu d'une mesure étalon empruntée à
l'histoire ou dérivée des ordonnances royales, il demandait à la
Législative de tirer l'unité de mesure fondamentale de la nature,
héritage commun à toute l'espèce humaine. Seul un étalon tiré de la
nature elle-même, déclara-t-il, serait susceptible d'être éternel [...]
D'ailleurs, il était tout à fait pertinent de fonder l'unité de mesure qui devait servir à tous les peuples de la Terre sur la mesure de la Terre elle-même. On avait là une parfaite adéquation avec les aspirations universelles de la Révolution. Comme Laplace devait le faire remarquer un peu plus tard, un mètre tiré de la mesure de
la Terre permettrait au plus humble des propriétaires de tenir des
propos tels que: «le champ qui fait [vivre] mes enfants est ue telle
portion du globe. Je suis dans cette proportion copropriétaire du Monde.» "
Ken Alder, Mesurer le monde, l'incroyable histoire de l'invention du mètre (Champs)
|
| Laplace était partie prenante d'une Comission de l'Académie
comprenant également Lagrange, Monge, Condorcet et Borda, dont le
cercle répétiteur devait s'avérer si utile aux mesures d'angles sur
lesquelles reposerait la triangulation du méridien de Paris. Elle
comporte en 1793 les six mathématiciens et les csix physiciens de
l'Académie, puis est "épurée" ("régénérée",
dira Monge), Laplace faisant partie de ceux qu'on écarte. Au plus fort
de la Terreur, il juge prudent de s'aloigner de Paris, et c'est chez
lui, à Melun, qu'on arrête l'astronome et académicien Bailly, devenu le
premier maire de Paris en 1789, à qui Laplace avait offert un refuge.
|

|
|
Jean-Sylvain Bailly, Maire de Paris, par J.-L. Mosnier
(musée Carnavalet, Paris)
|
La Convention Thermidorienne met fin à cette dure période, et, sous
l'impulsion de Lakanal, Carnot et Prieur de la Côte d'Or, fonde les
établissements qui contribueront durablement à l'excellence
scientifique française: l'École Normale de l'An III et l'École Polytechnique.
Laplace va jouer un trôle très différent dans chacune des deux. Suivons
lee d'abord dans la première, certes éphémère, mais qui devait marquer
durablement l'histoire après sa résurrection en École Normale Supérieure.
À l'École Normale de l'An III

|

|
| L'amphithéâtre Verniquet du Jardin des Plates, où se déroulèrent les cours de l'École Normale de l'An III |
Laplace va y donner un cours de mathématiques, assez bref
(10 leçons), mais comportant quelques innovations intéressantrs.
L'amphithêatre est plein à craquer: aux élèves viennent s'ajouter des
collègues, des conventionnels, des femmes même: c'est qu'une Révolution
est en marche! Un élève particulièrement affuté lous a laissé les notes dans lequelles il dresse le portrait de ses professeurs: Joseph Fourier, promis à un brillant avenir.
"Rien d'extraordinaire dans son cours?"
Voire! Certes, il recoupe assez nettement celui de Lagrange, car
l'objet essentiel de l'un comme de l'autre est la théorie des équations
algébriques. Il y aurait pu avoir une meilleure coordination, sans
doute, mais on se devra de le dire avec indulgence, au vu de la
rapidité -ne devrait-on pas dire plutôt l'urgence?- avec laquelle lz
nouvelle école est organisée, Le tournant pris en ce lieu, à cette
date, et qui servira dorénavant d'exemple au monde entier, c'est celui
d'un enseignement au contact de la recherche et de l'actualité
scientifique la plus récente. Le cours de Laplace nous en offre au moins trois exemples:
- Le premier est la "meilleure" (ou moins mauvaise?) démonstration pour l'époque du théorème fondamental de l'Algèbre, dit encore théorème de d'Alembert-Gauss. Elle figure dans sa cinquième leçon (11 Ventôse An III, 1er
Mars 1795) et elle est propre à son auteur: certes, elle comporte
encore des lacunes: d'une part, elle repose sur un théorème de la
valeur intermédiaire très consensuellement admis en ce temps-là, ce qui
n'est pas trop grave puisque l'avenir viendra, avec Bolzano et la
formalisation des nombres réels , combler ce vide. Mais d'autre part,
et c'est plus gênant, elle recèle une sorte de pétition de principe,
que ne manquera pas de critiquer Gauss: l'existence des racines a
priori comme quantités impossibles qu'il va manipuler algébriquement
pour montrer qu'elles sont racines, deux par deux, de polynômes du
second degré, ce qui consuira à une factorisation réelle du polynôme
donné;
- Le cours d'introduction aux probabiltés (dixième leçon, 21 Floréal An III, 10
Mai 1795) est à la fois une innovation sans précédent dans
l'enseignement, une conséquence de ses réflexions sur un sujet qu'
affine, de mémoire en mémoire, depuis ses débuts scientifiques,
et la préfiguration de l'ouvrage qu'il publiera ne 1814;
- Il modifie, annonce-t-il au début de sa neuvième leçon, (11 Floréal An III, 30 Avril 1795), l'ordonnancement de son cours pour traiter de l'actualité la plus récente, l'introduction du système métrique. Écoutons le:
Mètre référence, pour le public.
Sous les arcades, rue de Vaugirard.
Le seul de Paris encore à son emplacement d'origine (1796-97)
Observer la division décimale,
en décimètres puis centimètres dans la partie droite du mètre.
|
" J'interromps aujourd'hui l'ordre de ces leçons de mathématiques, pour vous entretenir du système des Poids & Mesures
qui vient définitivement d'être décrété par la Convention Nationale.
L'un des plus utiles objets qui vous occuperont, après être retournés
dans vos départements, sera de faire connaître à vos concitoyens, et
spécialement aux instituteurs des écoles primaires, ce bienfait des sciences et de la Révolution. Je vais donc l'exposer ici avec le détail dû à son importance.[...]
L'identité du
calcul décimal, et de celui des nombres entiers ne laisse aucun doute
sur la division de toutes les espèces en mesures décimales [...].
On ne balança donc point à adopter la division décimale, et pour mettre
de l'uniformité dans le système des mesures, on résolut de les dériver toutes d'une même mesure linéaire
et de ses divisions décimales. La question fut ainsi réduite au choix
de cette mesure universelle à laquelle on a donné le nom de mètre.
Pouur vous faire connaître les motifs qui, dans ce choix, ont guidé les
commissaires de l'Académie, il convient de rappeler, en peu de mots,
les principaux résultats que l'on a trouvés sur la figure de la terre,
et sur la variation de la pesanteur à sa surface."
|
 |
 |
Et puis, il y a la manière, qui prime sur la matière. Laplace émaille son cours d'invitations à consulter des ouvrages de référence:
"
Les bornes de cette leçon ne me permettent pas d'insister davantage sur
la théorie des courbes. On trouvera tous les détails, que l'on peut
désirer à cet égard, dans le second second volume de l'Introduction à l'Analyse des Infiniments petits, par Euler, et dans l'ouvrage de Cramer sur la Théorie des Courbes.
Ces deux ouvrages, quoiqu'excellents chacun dans leur genre, ne
dispensent pas de lire les deux ouvrages originaux qui leur ont donné
naissance, et qui, soit par eux-mêmes, soit par l'influence
qu'ils ont eu sur les sciences mathématiques, méritent toute
l'attention des géomètres: je veux parler de la Géométrie de Descartes, et du traité de Newton, intitulé: Énumération des Lignes du Troisième Ordre."
huitième leçon, (21 Germinal An III, 10 Avril 1795)
|

|

|

|

|
à former des sortes de séminaires d'approfondissement (quelle modernité!)
"
Je ne puis ici que tracer la route, en indiquant les vérités les plus
remarquables, et en vous laissant le soin de rétablir les vérités
intermédiaires et les démonstrations que je suis forcé de supprimer. J'exhorte
eux qui veulent approfondir ces matières à se réunir de temps en temps
pour cet objet. Je me ferai un devoir d'assister, le plus souvent qu'il
me sera possible , à ces conférences, heureux d'être utile à
ceux d'entre vous que leur goût et leurs talents appellent à
répandre les sciences mathématiques, et à reculer leurs bornes."
quatrième leçon (1er Ventôse An III, 19 Février 1795)
|
Même un sujet qui n'est ici qu'effleuré en quelques phrases lui
donne l'occasion de proposer des lignes de conduite universelles:
"
La méthode des limites sert de base au calcul infinitésimal. Pour
faciliter l'intelligence de ce calcul, il rest utile d'en faire
remarquer les premiers germes dans les vérités élémentaires qu'il
convient toujours de démontrer suivant les méthodes les plus générales. On donne ainsi aux aux élèves à la fois des connaissances et la méthode pour en acquérir de nouvelles.
En continuant de s'instruire, ils ne font que suivre la route qui leur
a été tracée, et dans laquelle ils ont contracté l'habitude de marcher;
et la carrière des sciences leur devient beaucoup moins pénible.
[...] Préférez donc, dans l'enseignement, les méthodes générales, attachez vous à les présenter de la manière la plus simple, et vous verrez en même temps qu'elles sont presque toujours les plus faciles."
septième leçon, (11 Germinal An III, 31 Mars1795)
| 
|
| L' ENS se souvient et lui rend hommage: il a son buste dans la fameuse "Cour aux Ermests" |
À l'École Polytechnique
Mais pourquoi Laplace, qui n'y enseigna jamais, se retrouvet-il au fronton de l'École Polytechnique, en bonne compagnie d'ailleurs -ses collègues de l'École Normale de l'An IIIt?


Au fronton de l'ancienne École
Polytechnique (Paris).
De
gauche
à droite: Lagrange, Laplace, Monge, Berthollet, Fourcroy
" À la différence de Monge, Laplace intervint
dans les affaires de l’École Polytechnique presque comme un deus ex
machina et non par décision personnelle. Il était resté en semi retraite
près de Melun pendant les mois de sa gestation. Il n’était pas
intervenu dans sa fondation ni dans la définition de son programme
original et n’y enseigna jamais. Sa contribution initiale vient de
l’extérieur.
[...]
Laplace avait été privé de son poste d’examinateur des élèves-officiers
de l’école d’artillerie – source importante de revenus - peu après la
dissolution de l’Académie des Sciences en août 1793. Le 23 juillet
1795, le Comité de Salut Public de Thermidor lui rendit son poste en
constatant qu’il n’aurait jamais dû en être privé. C’est ainsi
qu’au début de l’année scolaire 1795-96 quand les écoles d’application
furent subordonnées à l’Ecole polytechnique, Laplace se retrouva ipso
facto examinateur des polytechniciens candidats à l’admission à l’école
d’artillerie. De plus, lui-même et Bossut qui avait été aussi rétabli
comme examinateur des élèves officiers du Corps des Ingénieurs, furent
examinateurs au concours de l’Ecole polytechnique même. Participant aux
sélections à l’entrée et à la sortie, Laplace assisté de Bossut était
en position de chien de garde sur l’ensemble du cursus.
À
la fin de la première année, Laplace ne fut pas satisfait des méthodes
et des résultats. Dans une lettre au Directeur en décembre 1796 il fit
des recommandations tant pour l’admission que pour le programme d’études."
|
Voici un extrait de cette lettre, que l'on pourra lire intégralement avec un commentaire approfondi de Janis Langins dans cet article (en ligne) . Laplace propose une modification du concours:
" J'ai rendu compte aux ministres, avec la plus exacte impartialité, & sans indulgence, du résultat de mes examens ; parce que je leur dois la pure vérité. Vous me faites l'honneur de m'écrire que le Conseil de l'école polytechnique est disposé à faire dans l'enseignement de l'école, les changemens qui seront jugés utiles. Veuilles bien lui faire part des observations suivantes, si elles vous paroissent mériter son attention.
Le premier changement à faire est celui du mode d'admission à l'école polytechnique. Il est vicieux à tous égards; comme le jury chargé de prononcer sur cette admission l'a fait connoistre au ministre de l'intérieur, le meilleur mode à suivre seroit un examen fait par un seul examinateur ; mais le concours est trop considérable, pour qu'une seule personne puisse se charger de cet examen. On a proposé d'en charger les deux examinateurs pour l'hydrographie & un troisième examinateur qui se rendroient à des époques déterminées, dans plusieures villes de l'intérieur de la France. Ensuite (?) un jury formé de ces trois examinateurs, & des deux examinateurs de l'école polytechnique, classeroit les sujets examinés, suivant l'ordre de leur mérite. Il n'est pas douteux que ce mode est beaucoup meilleur que le mode actuel.
Pour que les examinateurs ayent une mesure commune, je propose, non d'adopter un cours particulier, pour ces examens ; mais de faire imprimer une liste très détaillée des propositions sur les quelles les élèves seraient interrogés. Ce seroit une table de matières d'un cours de mathématiques, que l'on pourroit de teins en tems, modifier ou étendre; les professeurs auroient la liberté d'y adopter les demonstrations qu'ils jugeroient les meilleures. Il me paroist inutile de s'enquêrir, comme on le fait, des connoissances supplémentaires. Mais il faut estre très sévère sur celles qui sont exigées."
Laplace au Citoyen Directeur, 19 Frimaire An V (19 Février 1795)
|
Voilà une innovation remarquable: la rédaction d'un programme précis
du concours, clairement borné, afin que les examinateurs puissent, de
manière égale, évaluer les candidats sur le programme, tout le
programme, mais rien que le programme!
Cela peut nous paraître banal
aujourd'hui, car c'est une norme qui s'est imposée pour tous les
concours d'accès aux grandes écoles scientifiques, mais c'est une
première. Et pendant plus de deux siècles, aucun concours ne verra des
examinateurs aussi (légitimement) sourcilleux sur ce point: tentez un
léger hors programme à l'oral, et l'on vous ramènera, poliment mais
fermement, à n'user que les moyens réglementairement à votre
disposition.
Mais il faut aussi, ajoute-t-il, réformer l'enseignement dans l'École,
et en tout premier lieu renforcer la part de l'analyse, qui n'avait
guère les faveurs d'un Monge avant tout prosélyte de sa géométrie
descriptive... C'est pourtant un jeune homme arrivé dans les bagages de
Monge à la fondation de l'École,
qui inaugurera avec la première promotion un cours d'analyse plus
"ouvert" que celui de Lagrange, puisant largement dans les idées
d'Euler, Laplace bien sûr... et les siennes propres: le citoyen Joseph Fourier!
faie
" Quant à l'enseignement des mathématiques dans l'école polytechnique, je regarde comme indispensable qu'au moins de deux jours l'un, les élèves ayent une leçon d'environ deux heures sur l'analyse & la mécanique. La première moitié de la leçon seroit employée à faire répéter aux élèves, la leçon précédente ; la seconde moitié le seroit à leur expliquer une nouvelle leçon ; il faut de plus que chaque jour, les élèves puissent travailler par eux mesmes, deux heures au moins. L'instruction générale doit porter sur les principes élémentaires & fondamentaux
des sciences mathématiques ; elle doit estre proportionnée à l'intelligence du plus grand nombre des élèves car dans une école de service public, il importe plus d'avoir beaucoup de sujets, suffisamment instruits, qu'un petit nombre de sujets très forts. Cependant, il est à désirer que ceux qui ont beaucoup d'intelligence puissent trouver dans l'école, les moyens de perfectionner leur instruction ; car c'est d'eux principalement, que les arts aux quels ils sont destinés, attendent leurs progrès."
Laplace au Citoyen Directeur, 19 Frimaire An V (19 Février 1795)
|
On retrouve ici, sous une autre forme, les idées qu'il a défendues à l'École
Normale: former raisonnablement l'ensemble, tout en permettant aux
talents de s'exprimer et en leur fournissant tout le soutien désirable.
En position de force, fût-elle des plus éphémère, le ministre de l'Intérieur Laplace va créer, par la loi du 25 Frimaire An VIII (16 Décembre 17899), le Conseil de Perfectionnement.
Il était temps... moins de dix jours aprèsm, Laplace ne sera plus ministre, comme on va le voir plus bas!
Ce conseil est composé de 2 examinateurs d'analyse), 2 examinateurs parmi les 3
disciplines: géométrie, chimie et physique, 3 membres de l’Institut, 4
représentants élus des professeurs et des représentants des diverses
écoles "d'application" de l’Ecole polytechnique. L'idée est claire:
mêler aux enseignants ceux qui vont recevoir leurs élèves (avec les
récriminations que l'on peut imaginer sur les manques et tout ce qu'on
leur aura appris d'inutile à la place...) et ceux qui sont au courant
des dernières avancées des sciences et techniques. Du haut de ce
conseil, un peu plus de deux siècles de débats houleux nous
contemplent, entre une vision utilitariste et un désir d'être à la
pointe des sciences: il y a là matière à un livre entier, mais, du
moins, ces débats ont eu lieu! Laplace, qui le préside, en restera membre jusquen 1816.

|

|

|
|
1807 ou 1816, un peu(!) de "cirage de pompes" à l'égard du souverain ne peut pas nuire...
textes complets disponibles sur Google Books: 1807, 1815-16
|
Il a donc été fort judicieux, dans cette école, de placer sa
statue... à l'entrée de la salle des Conseils! (Elle n'a pas toujours
été là...)
Du Consulat à l'Empire

A.-J. Gros, Napoléon Bonaparte en Premier Consul (1802)
|
Le coup d'État du 18
Brumaire (9/11/1799) met fin au Directoire, et le 20, le Consulat est
en place, avec trois consuls provisoires. Bonaparte est déjà le Premier
Consul. Le 21, seulement trois jours après la prise de pouvoir de ce
dernier, voilà Laplace nommé par lui Ministre de l'Intérieur! Un peu
surpris, mais il est loin de détester les honneurs...
Il décevra rapidement à ce poste, sera brutalement limogé le 25
Décembre, mais en se voyant offrir un poste à la fois prestigieux et...
moins stratégique: Chanceliert du Sénat Conservateur,
l'assemblée chargée de vérifier la conformité des lois à la
Constitution. L'homme fort du régime se serait étonné, et fâché, de
voir celui qui avait mis de l'ordre dans les cieux n'avoir mis que six semaines pour désorganiser complètement l'administration du pays.
|
Ce qui est sûr, puisque les écrits restent -c'est bien connu- c'est ce que Napoléon en exil dicta à Las Cases dans le Mémorial de Sainte-Hélène:
| " Géomètre de première catégorie, Laplace n'a pas tardé à se montrer un administrateur plus que médiocre;
dès son premier travail nous avons immédiatement compris que nous nous
étions trompés. Laplace ne traitait aucune question d'un bon point de
vue : il cherchait des subtilités de partout, il avait seulement des
idées problématiques et enfin il portait l'esprit de l'infiniment petit jusque dans l'administration. " |
|

Z. Belliard d'après Ch. Steuben:
Napoléon à Sante-Hélène, dictant ses Mémoires au général Gourgaud
|
|
Caprice de l'Histoire, c'est M. le Chancelier du Sénat Laplace qui recevra
l'abdication de l'Empereur, le 12 Avril 1814. Car c'est le Sénat qui avait
prononcé cette déchéance le 3.
| 
| 
|
A Montfort, darès H. Vernet:
Les Adieux de Fontainebleau le 20/04/1814
|
Abdication de Napoléon
(Archives Nationales & Wikimedia Commons)
|
Fourier (qui s'y connaît, il est vrai, en matière de disgrâce) a
bien raison de remettre à leurs places respectives les divers rôles, en
fonction de leur importance sur le long terme:
"
Je pourrais, je devrais peut-être, rappeler les hautes dignités
politiques dont il fut revêtu; mais cette énumération n'appartiendrait
qu'indirectement à l'objet de ce discours. C'est le grand géomètre dont
nous célébrons la mémoire. Nous avons séparé l'immortel auteur de la
Mécanique Céleste de tous les faits accidentels qui n'intéressent ni sa
gloire, ni son génie. En effet, Messieurs, qu'importe
à la postérité, qui aura tant d'autres détails à oublier, d'apprendre
que Laplace fut quelques instants ministre d'un grand état? Ce qui
importe, ce sont les vérités éternelles qu'il a découvertes; ce sont
les lois immuables de la stabilité du monde, et non le rang qu'il
occupa quelques années dans le sénat qu'on dit conservateur.
Ce qui importe, Messieurs, et plus encore peut-être que ses
découvertes, ce sont les exemples qu'il laisse à tous ceux à qui les
sciences sont chères; cc'est le souvenir de cette persévérence
incomparable qui a soutenu, dirigé couronné tant de glorieux efforts."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|
Le Mécanicien du Ciel
"
Laplace avait reçu de la nature toute la force du génie que peut exiger une entreprise immense. Non seulement oil a réuni dans son Almageste du 18e siècle
ce que les sciences mathématiques et physiques avaient déjà inventé;
mais il a ajouté à cette science des découvertes capitales qui lui sont
propres, et qui avaient échappé à ses prédécesseurs. Il a résolu, soit par ses propres méthodes, soit par cellels qu'Euler et Lagrange avaient indiqué les principes, les questions les plus importantes, et certainement les plus difficiles de toutes celles que l'on avait considéré avant lui.
Sa constance a triomphé de tous les obstacles. Lorsque ses premières
tentatives n'ont point eu de succès, il les a renouvelées sous les
formes les plus ingénieuses et les plus diverses."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|

| 
|
Á l'Observatoire de Paris, Laplace est statufié, face à Cassini,
dans une pause relativement similaire: assis, en pleine réflesion, ses
livres aux pied et une tablette à la main, là aussi, comme Cassini!
Pourtant, les deux savants sont très différents dans leurs
contributions. Cassini est un observateur, un astronome, alors que
Laplace est avant tout un théoricien, ce qui lui vaudra le surnom
élogieux de Newton français.
|
Lers de notre première rencontre, le marbre ne semblait pas en très bon état, comme "piqué" de tâches noires...
Depuis, elle a fait l'objet d'un nettoyage-repolissage qui lui a rendu toute sa splendeur.
|
Les contributions de Laplace à
la mécanique céleste commencent très tôt, dès les premiers travaux
qu'il soumet, avant son entrée à l'Institut. Ansi, en 1771, un de ses papiers est ttitré -déjà, comme préfigurant le monument à venir et ses ambitions- "Une Théorie Générale du Mouvement des Planètes". Les
écrits se succèdent, avec des thèmes de prédilection qui reviennent de
mémoire en mémoire: perturbations de l'ellipse keplérienne par les
satellites de la planète ou les planètes voisines, mouvement de la
Lune, système Jupiter-Saturne (5 années jupitériennes valent presque
exactement 2 années saturniennes, résonance qui induit des effets particuliers), anneaux de Saturne... Mais au fait, qu'y a-t-il de gravé sur la tablette de travail Laplace? Sur quoi médite-t-il?
Saturne et ses anneaux, bien sûr!
Les chefs d'œuvre viendront après la Révolution, quand Laplace sentira qu'il est temps, d'une part
de regrouper ces articles dont chacun affine le précédent, et d'autre
part d'englober ces études de parties différentes du système solaire en
un seul opus...
Mais il commence par un remarquable tour de force: lui qui aligne
sur ces sujets des calculs plutôt impressionnants, il publie en 1796 un ouvrage de présentation de l'ensemble qui ne contient pas une seule formule mathématique!
Un ouvrage descriptif, une narration en Français, a priori lisible par
tout un chacun (sans doute vaut-il mieux posséder un vocabulaire de
base, incluant mots et expressions: savoir ce qu'est une ellipse, comprendre ce que veut dire attraction en raison inverse du carré de la distance...)
|
|
Les amateurs de systèmes différentiels et de développement en
séries des perturbations n'auront pas trop à attendre: en 1798 (An VII)
paraissent les deux premiers volumes de l'ouvrage qui le sacrera comme
le spécialiste européen (et donc mondial, en ce temps-là) incontesté de
la question : sa Mécanique Céleste: tome 3 en 1802 (An XI), tome 4 en 1805 (An
XIII), La touche finale, le tome 5, comportant d'importants éléments
historiques, attendra 1825 (le calendrier républicain est abandonné
depuis bien longtemps...)
On sourira en voyant, au fil des ans, le Citoyen virer au Marquis à
particule, et la liste des titre prestigieux s'allonger sur la
couverture. Laplace y était fort sensible, et il n'en avait volé aucun.
" Le temps qui seul dispense avec justice la gloire littéraire, qui livre à l'oubli toutes les médiocrités contemporaines, perpétue le souvenir des grands ouvrages. Eux seuls portent à la postérité le caractère de chaque siècle. Ainsi le nom de Laplace vivra dans tous les âges."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|
D'une réplique légendaire (mais peut-être apocryphe) à un problème fondamental
Il faut ici dissiper un malentendu, fût-il anecdotique.
C'est (le plus
probablement) en présentant au Premier Consul son
tome 3, avec sa lyrique dédicace, dont on peut lire le début ci-contre,
que Laplace eut avec lui cet échange, s'il n'est pas apocryphe:
BONAPARTE : - Newton a parlé de Dieu dans son Livre. J'ai déjà parcouru le vôtre, et je n'y ai pas trouvé ce nom une seule fois.
LAPLACE : Citoyen Premier Consul, je n'ai pas eu besoin de cette hypothèse.
(cité par H; FAYE, "de l'Institut", Sur l'Origine du Monde,
Théories cosmogoniques des Anciens et des Modernes, Gauthier-Villars 1884)
|
moult fois cité, y compris en images glanées sur la toile (dans lesquelles on pourra traquer
les anachronismes vestimentaires, et se demander si le personnage...
est bien Laplace!)
|
|
Une majorité de commentateurs y lisent la manifestation de
l'athéisme de Laplace. Cette option philosophique du personnage est
avérée. Mais, que
le Chancelier du Sénat en fît la brutale affirmation à celui qui venait
de signer le Concordat serait bien peu protocolaire, encore moins
courtisan!
Ce n'est pas de l'athéisme que manifeste Laplace, c'est de l'orgueil -orgueil légitime au demeurant. Pour le comprendre, relisons avec lui Newton:

Issaac Newton
Trinity College, Cambridge
|
"
Je ne puis m'empêcher ici d'observer combien Newton s'est écarté, sur
ce point, de la méthode dont il a fait d'ailleurs de si heureuses
applications. Depuis la publication de ses découvertes sur le système
du monde et sur la lumière, ce grand géomètre, livré à des spéculations d'un autre genre,
rechercha par quels motifs l'auteur de la nature a donné au système
solaire la constitution dont nous avons parlé. Après avoir exposé, dans
le scolie qui termine l'ouvrage des Principes(1),
le phénomène singulier du mouvement des planètes et des satellites dans
le même sens, à peu près dans un même plan, et dans des orbes presque
circulaires, il ajoute:
«Tous ces mouvements si réguliers n'ont point de causes mécaniques [...] Cet admirable agencement du Soleil, des planètes et des comètes ne peut être que l'ouvrage d'un être intelligent et tout-puissant.»
Il reproduit à la fin de son Optique, la même pensée [...] :
«Un destin aveugle ne pouvait jamais faire mouvoir ainsi toutes les planètes, à quelques inégalités près à peine remarquables, et qui probablement deviendront plus grandes par une longue suite de temps, jusqu'à ce qu'enfin ce système ait besoin d'être remis en ordre par son auteur.»[...]
(1)
Ce scolie ne se trouve point dans la première édition de l'Ouvrage. Il
paraît que Newton jusqu'alors s'était uniquement livré aux sciences
mathématiques, qu'il a, malheureusement pour elles et pour sa gloire, trop tôt abandonnés."
in Exposiion du Système du Monde, Livre V, chap.6
|
Pas tendre, Laplace, dans sa note! Quoiqu' irréprochablement exact.
L'anecdote serait-elle futile, ou inventée, elle révèle une question
sérieuse et extraordinairement complexe, et Newton en est bien
conscient:
Le système solaire est-il stable?
Car si Newton a démontré rigoureusement par sa loi d'attraction l'orbite elliptique, découverte par Képler, c'est en faisant comme si chaque planète était seule en tête à tête avec le Soleil... ce qui est en contradiction avec le caractère universel
de cette attraction, son génial chef d'œuvre! Et cela complique tout,
et gravement en théorie (on ne le saura que beaucoup plus tard, avec
Poincaré à l'aube du XXème siècle, mais dès trois corps en interaction, tout calcul explicite des trajectoires est impossible).
Toute bonne physique est faite d'approximations, d'actions négligées
avec pertinence, et c'est le cas dans ce problème. Newton le sait, et
c'est pourquoi il redoute ces inégalités
(comprendre: altérations de l'ellipse calculée) , pas à brève échéance,
certes, mais dont l'importance pourrait s'accroître au cours du temps,
jusqu'à risquer l'éjection d'une planète hors du système, ou la
collision de deux d'entre elles... Pour garantir la stabilité, il faut
que quelqu'un, ou quelque chose agisse!
"
Le sytème de tous ces corps est constitué de manière que la masse du
Soleil surpasse considérablement celle des planètes; en sorte que l'on
peut, dans une première approximation, négliger, avec Newton, leur action les unes sur les autres et sur le soleil. Alors elles obéissent exactement aux lois de Képler. [...]
Newton
n'a point considéré les perturbations que l'action des planètes sur le
soleil et entre elles-mêmes produit dans leur mouvement elliptique;
seulement il fait voir que [...] l'action de Jupiter sur Saturne, dans
la conjonction de ces planètes, étant à l'action du Soeleil sur Saturne
dans le rapport de l'unité à 211, elle ne doit point être négligée. [...]
Le dérangement correspondant de Jupiter est environ six fois plus
grand, quoique l'action de Saturne sur Jupiter ne soit, à la pesanteur
de Jupiter sur le Soleil, que dans le rapport de l'unité à 500 [...] "
in Mécanique Céleste, t.5, Livre XV.chap.1
|
Voilà pourquoi Laplace va commencer par étudier longuement, dans une
succession de mémoires, le ménage à trois du Soleil, de Saturne et de
Jupiter... avec ses perturbations. L'idée n'est pas neuve: Euler,
Clairaut, d'Alembert s'y sont déjà frottés, et la méthode consiste,
sans jeter l'ellipse, à considérer que ses éléments caractéristiques, comme son axe, son excentricité, son inclinaison, varient lentement
et de trouver des formules (approchées, bien sûr) rendant compte de ces
variations. Les forces perturbatrices, quant à elles, seont développées
en séries, tronquées à tel ou tel rang on est toujours sans une
approximation, mais plus fine, et c'est la seule façon de pouvoir
soumettre les phénomènes au calcul.

|

|

|
|
Trois mémoires successifs, respectivement soumis à l'Académie en 1784, 1785 et 1787, sur les perturbations des orbites.
textes complets à retrouver dans le tome XI des Œuvres Complètes (sur Gallica, BnF)
|
Particulièrement pédagogue, Laplace justifie la
terminologie dans le premier, en reprenant, presquà la
lettre, les craintes formulées par Newton:
"
[...] les autres altèrent les éléments des orbites par des nuances presque insensibles à chaque révolution des planètes; mais ces altérations, en s'accumulant sans cesse, finissent par changer entièrement la nature et la position des orbites; comme la suite des siècles les rend très remarquables, on les a nommées inégalités séculaires."
|
Ce que Laplace va réussir à établir dans le tome 3 de la Mécanique Céleste -au prix de longs calculs!- c'est que ces variations restent bornées, dans des limites raisonnables, et donc que le système solaire est stable en tenant compte des perturbations mutuelles des corps, mais évidemment à un certain ordre d'approximation de ces perturbations.
Bref, tout résulte de la loi de Newton et des calculs... donc, très
littéralement, au premier degré, sa réponse à Bonaparte énonce une
vérité dont il est fier: il n'a pas eu besoin de l'hypothèse d'une correction divine: il a fait mieux que Newton!
Pas eu besoin de la correction par Dieu, ce n'est donc pas, stricto sensu, pas besoin de l'hypothèse de l'existence de Dieu... ceci posé, Laplace est un esprit fin, qui se sera sans doute délecté du second degré de sa réplique... s'il l'a prononcée!
Sans entrer dans le détail, il est intéressant de dire un mot de la
manière dont s'y est pris Laplace, car elle s'insère dans une histoire
mathématiquement loin d'être terminée, mais particulièrement
fructueuse.
Il a réussi dans sa Théorie de Jupiter et Saturne à obtenir la constance des demi-grands axes, mais ce sont surtout les excentricités et inclinaisons qui l'inquiètent.
" [...] j'obtins, pour les déterminer, un nombre d'équations différentielles linéaires du premier ordre double de celui des planètes [...] La forme très simple des équations différentielles des éléments elliptiques auxquelles j'étais parvenu me fit reconnaître un des éléments les plus iimportants du système du monde, sa stabilité. Ces
équations étant linéaires à coefficients constants, leur intégration
donne l'expression finie de chacune des variables par une suite de
sinus et de cosinus d'angles croissant proportionnellement au temps, et
dont
les coefficients du temps dans chaque angle sont les racines d'une
équation algébrique d'un degré égal au nombre des planètes. Si
toutes les racines sont réelles et inégales, ces diverses expressions
sont périodiques et les variables restent toujours fort petites; le
système des planètes ne fait donc alors qu'osciller autour d'un état
moyen, dans d'étroites limites. Mais,
si quelques unes des racines étaient imaginaires ou égales entre elles,
les sinus et les cosinus correspondants se changeraient en
exponentielles ou en arcs de cercle, qui, croissant indéfiniment avec
le temps, donneraient aux variables de grandes valeurs et
changeraient considérablement la forme des orbite. Heureusement, je
suis parvenu d'une manière fort simple "
in Mécanique Céleste, t.5, Livre XV.chap.1
|
La traduction de ce texte en langage mathématique moderne sera un bon
exercice de compréhension des principes du cours pour un étudiant de
premier cycle... Laplace sait que les solutions d'un système
différentiel sont des combinaisons de sinus et cosinus, d'exponentielles,
ou de produits de telles fonctions par un polynôme du temps, et il doit
montrer qu'elles sont toutes de la première forme.
Il a pu "découpler" son sytème en deux systèmes 7×7, fort bien, mais que faire avec chacun d'eux? Nous dirions aujourd'hui: réduire la matrice, et pour cela former son polynôme caractéristique, connaître la nature de ses racines (les valeurs propres):
réalité, signe, multiplicité... mais gare aux anachronismes: le
véritable inventeur des valeurs propres, c'est Fourier en 1807, et la
première évocation du polynôme caractéristique, Le Verrier en 1839. Les
14 tomes des écrits de Laplace
plaident pour sa défense: il est tout sauf un froussard face aux
calculs! Mais là (imaginez vous, heureux étudiants -comme pourrait dire Droopy-, en train de calculer un déterminant 7×7...),
ça devient inhumain, alors il cherche et trouve un subterfuge pour s'en
sortir autrement, sans calcul explicite des racines.
Le calcul effectif de ces valeurs propres sera le premier triomphe, en 1839, de Le Verrier, qui en fera la
détermination par la méthode numérique qu'il invente
ad hoc: vous trouverez tous les détails de l'exploit dans notre page
spéciale et notre lecture accompagnée de son article, sur le site BibNum.
Faut-il le préciser? Tout aussi "bulldozer à calculs" que Laplace, il
ne calculera pas davantage le polynôme caractéristique (le déterminant
a plus de 5000 termes!)
Pour en revenir à Laplace, il a employé un stratagème à base d'intégrales premières de son système différentiel pour obtenir la relation
où les lettres m, a, e désignent masse, demi-axe et excentricité, l'indice i indiquant la planète.
|
Pour en savoir un petit peu plus (mais vous pouvez sauter aussi...)
Avec le choix de variables fait par Laplace : pi = ei cos ϖ et qi = ei sin ϖ ( ϖ est un angle fixe du problème), il réussit à mettre le système sous la forme:
Les bi,r, sont tels que bi,r = br,i et bi,i = 0 (puisqu'on a isolé en tête ce qui concerne la variable d'indice i)
Laplace multiplie la première par qi, la seconde par pi, afin de faire sisparaître les premiers termes au second membre
Il multiplie par 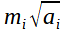 , puis somme sur i : au second membre, chaque terme apparaîtra une fois précédé de +, une fois précédé de - : ils se détruisent deux à deux (grâce à la symétrie des coefficients bi,r ci-dessus mentionnée), si bien que le second membre est nul. , puis somme sur i : au second membre, chaque terme apparaîtra une fois précédé de +, une fois précédé de - : ils se détruisent deux à deux (grâce à la symétrie des coefficients bi,r ci-dessus mentionnée), si bien que le second membre est nul.
La quantité sous le
crochet est donc constante (on a intégré une fois cette combinaison des
équations, ce qui explique la terminologie intégrale première); or par le choix des variables
pi² + qi² = ei²
d'où le résultat... une méthode très simple, dit textuellement Laplace!
d'après le Mémoire sur les Variations Séculaires des Orbites des Planètes (1787) in Œuvres complètes, t.XI
|
Fourier ne manque pas de célébrer ce triomphe avec un rythme qu'on
retrouvera plus tard dans d'autres pièces vouées à une gloire éternelle:
"
Dans cet ensemble de recherches, on doit remarquer surtout celles qui se rapportent à la stabilité des phénomènes: aucun objet n'est plus digne de la méditation des philosophes.[...]
La forme des grzndes orbites planétaires, leurs inclinaisons, varient
et s'altèrent dans le cours des siècles; mais ces cha,ngements sont
limités. Les dimensions principales subsistent, et cet immense
assemblage des corps célestes oscille autour d'un état moyen vers
lequel il est toujours ramené. Tout est disposé pour l'ordre, la perpétuité et l'harmonie."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
| 
Henri Matisse, Luxe, calme et volupté (1904)
Musée d'Orsay, Paris
|
|
" Là, tout n'est qu'ordre et beauté,
Luxe, calme et volupté. "
Charles Baudelaire, L'invitation au voyage in Les Fleurs du Mal (1857)
|
Le Crépuscule
Laplace décède à Paris, le 5
Mars 1827, dans sa maison, 108 rue du Bac. Il y avait emménagé en 1816
après la dissolution du Sénat Conservateur par un Louis XVIII avant
tout soucieux de faire disparaître le plus possible de traces de la
Révolution et de l'Empire. Certes, le sénateur Laplace avait été promu
Pair de France, mais il ne bénéficiait plus de l'avantage en nature que
lui conférait son titre de Chancelier du Sénat: loger au Palias du
Luxembourg. Il n'avait ainsi pas trop de chemin à faire pour se rendre
à l'Institut!
|
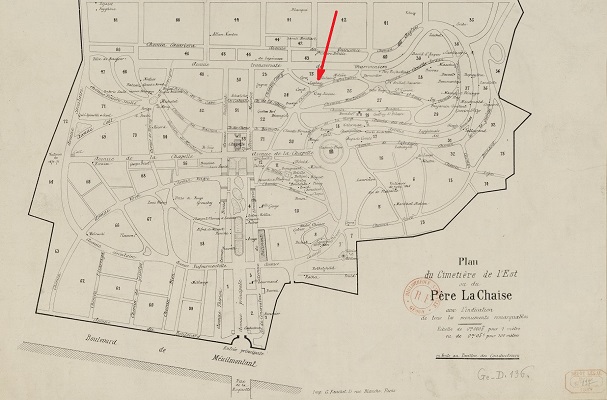
Il fut inhumé dans la 25ème division du Père Lachaise, comme l'indique ce plan de 1883; et le chemin séparant les 24ème et 25ème divisions fut, du coup, nommé en son honneur. Mais ses cendres et celles de son
épouse furent transférées en 1888 dans un petit mausolée à l'allure de temple dorique, dans le village de Saint Julien
de Mailloc (Calvados), sur l'initiative de leur petite fille. Le
monument du cimetière du Père Lachaise prit quant à lui la direction de
celui de son village natal où il fut installé comme glorieux cénotaphe
de l'enfant du pays. |

| 
| 
|
|
|
dessin de la sépulture au Père Lachaise.
(source: ce blog)
|
à Saint Julien
de Mailloc
(source: Wilipedia anglais!)
|
" Le temps qui seul dispense avec justice la gloire littéraire, qui livre à l'oubli toutes les médiocrités contemporaines, perpétue le souvenir des grands ouvrages. Eux seuls portent à la postérité le caractère de chaque siècle. Ainsi le nom de Laplace vivra dans tous les âges."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|
Hommages
Les anniversaires liés à Laplace ont été dignement célébrés;
parmi les discours et articles, relevons ceux d'Émile Picard,
mathématicien bien connu, du père du Big Bang, Georges Lemaître dans un
article orné d'une belle médaille: Laplace et la Mécanique Céleste ( du journal L'Astronomie n°64, mis en ligne par la NASA, merci à elle!), d' André Danjon, directeur de l'Observatoire de Paris de 1945 à 1963, du mathématicien et académicien Jean Chazy, auteur de travaux en mécanique céleste sur le Problème des Trois Corps.
Les textes de Picard, Danjon, et Chazy figurent in extenso à la suite de l'éloge prononcé par Fourier, sur le site de l'Académie des Sciences.
Puisse le Bicentenaire 2017 être lui aussi marqué par de belles commémorations!
Laissons à ce fin orateur qyu'est Fourier le soin de conclure...
non sans remarquer la similitude de style et d'esprit de son envoi avec
les ultimes propos de la préface de sa Théorie Analytique de la
Chaleur: de nouvelles données seront sans doute recueillies, grâce à de
meilleurs appareils, mais la théorie mathématique vaut pour l'éternité.
C'est là aussi, d'un connaisseur -de son inventeur, doit on plutôt
dire- un grand credo en la Physique Mathématique!

|
" Vos
successeurs, Messieurs, verront s'accomplir les grands phénomènes dont
il a découvert les lois. Ils observeront dans les mouvements lunaires
les changements qu'il a prédits et dont lui seul a pu assigner la
cause. L'observation continuelle des satellites de jupiter perpétuera
la mémoire de l'inventeur des théorèmes qui en règlent le cours. Les
grandes inégalités de Jupiter et de Saturne, poursuivant leurs
longues périodes, et donnant à ces astres des situations nouvelles,
rappelleront sans cesse une de ses étonnatres découvertes. Voilà
des titres d'une gloire véritable, que rien ne peut anéantir. Le
spectacle du ciel sera changé, mais à ces époques reculées, la gloire
de l'inventeur subsistera toujours: les traces de son génie portent le
sceau de l'immortalité."
Joseph Fourier, Éloge historique de M. le Marquis de Laplace.
Académie Royale des Sciences, 15/06/1829
|
cicontre: portrait à l'Observatoire de Paris.
|
Références
- J. DHOMBRES, Pierre-Simon de Laplace, le parcours d'un Savant (Hermann)
- J. DHOMBRES & alias, Leçons de Mathématiques de l'École Normale de l'An III (Dunod)
- C.C. GILLISPIE, Pierre-Simon Laplace, A Life in Exact Science (Pronceyon University Press)
- J. LASKAR La Stabilité du Système Solaire in A. DAHAN-DALMEDICO, J.L. CHABERT & alias, Chaos & Déterminisme (Points Sciences)
- (G -disponible en ligne sur Gallica-BnF)
Mécanique
Céleste

















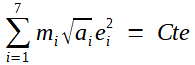
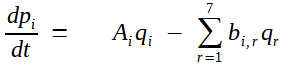
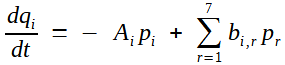
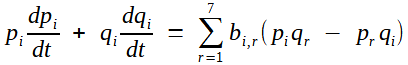
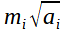 , puis somme sur i : au second membre, chaque terme apparaîtra une fois précédé de +, une fois précédé de - : ils se détruisent deux à deux (grâce à la symétrie des coefficients bi,r ci-dessus mentionnée), si bien que le second membre est nul.
, puis somme sur i : au second membre, chaque terme apparaîtra une fois précédé de +, une fois précédé de - : ils se détruisent deux à deux (grâce à la symétrie des coefficients bi,r ci-dessus mentionnée), si bien que le second membre est nul.